帶擴散項的Cahn-Hilliard方程解的適定性
李書嵐, 蒲志林
(四川師范大學 數學科學學院, 四川 成都 610066)
本文研究如下帶擴散項的廣義Cahn-Hilliard方程的初邊值問題
(x,t)∈Ω×R+,
(1)
(2)
u|t=0=u0,
(3)
其中,Ω?Rn(n=1,2,3)是有界正則區域,且具有光滑邊界Γ,ν為邊界上的單位外法向量,Δ為Laplace算子,f(u)為一對數型函數F(u)的導數,g(u)稱為擴散項.
在方程(1)中,若g(u)=0,則稱其為Cahn-Hilliard方程(簡稱CH方程),是數學物理上一類重要的非線性偏微分方程,它描述了與相分離過程相關的兩相系統的重要定性特征.1958年,Cahn和Hilliard[1]首次基于熱力學提出了相關模型,近幾十年來,國內外眾多學者對其進行了廣泛研究,尤其是解的存在性、唯一性、正則性,以及相關動力系統的漸近性等[2-5].
然而,目前在Neumann邊界條件下對帶一般的非線性擴散項的CH方程的研究相對較少,為了增加此類數學模型的適用范圍,并推廣一些已有結果,本文將在現有研究基礎上對具有更一般非線性擴散項的方程(1)~(3)進行解的先驗估計,得到弱解的存在唯一性,進而還得到解的相關正則性.
1 主要假設和記號

f′(s)≥-c0,c0≥0,s∈R,
(4)
f(s)s≥c1F(s)-c2,F(s)≥-c3,
c1>0,c2,c3≥0,s∈R,
(5)
|f(s)|≤F(s)+c, ?>0,s∈R, (6)
(7)
g′(s)≥-c4,c4≥0,s∈R,
(8)
|g(s)|≤c5(1+|s|2q+2),s∈R,
(9)
其中p≥2q+1.由于4q+4≤2p+2,則有
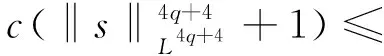
?>0,s∈R.
(10)
令H=L2(Ω),V=H1(Ω),且定義〈u〉為空間平均,表示為
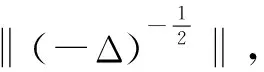
2 主要結果及其論證
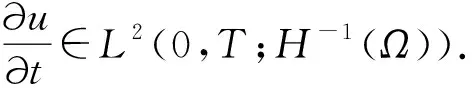
證明首先證明存在性.為了得到解的存在性,先要得到uN與N無關的先驗估計.以下用到的所有常數都是與N無關.考慮如下近似問題,其中N∈N,
(x,t)∈Ω×R+,
(11)
uN|t=0=u0.
首先,在Ω上對(11)式進行積分可得
(12)
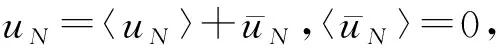
等價地,上式可以寫成下面的形式
(13)

其中根據假設(4)和插值不等式可得
(15)
再由假設(9)和Young不等式可得
(16)
′>0,
(17)
根據(14)~(17)式可得
(18)
將〈uN〉與(12)式做內積可得
c‖g(uN)‖L1(Ω)|〈uN〉|,
(19)
根據連續嵌入L2(Ω)?L1(Ω)可得

(20)
將(18)和(20)式相加可得
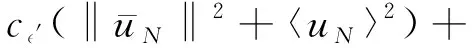
?′>0.
(21)
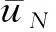
(22)
其中
((f(uN),uN))-((f(uN),〈uN〉)),根據假設(5)式可得
((f(uN),〈uN〉))≤c‖f(uN)‖L1(Ω)|〈uN〉|,根據假設(6)式可得
‖f(uN)‖L1(Ω)≤
再根據假設(5)和(7)式可得F有界,則有
(23)
由(22)~(23)式可得
(24)
將(21)和(24)式相加可得
根據連續嵌入L4q+4(Ω)?L2(Ω),q≥1,再根據假設(10)則有
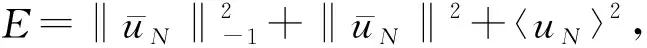
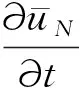
(25)
其中
(26)
c‖f(uN)‖L1(Ω)‖g(uN)‖≤
c‖g(uN)‖2+c′,
(27)
(28)
根據(25)~(28)式可得
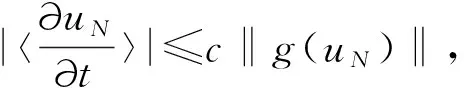
(30)

(31)
其中
(33)
(34)
根據(30)~(35)式和(20)式,結合假設(10)可得
>0.
(35)
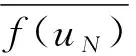
(36)
其中
(38)
(39)
由(36)~(39)式可得
(40)
并且
(41)
根據(40)和(41)式,結合前面的估計可得f(uN)在L2(0,T;L2(Ω))中有界.
接下來,根據上述的先驗估計結果,結合標準的Aubin-Lions緊性結果,當N→+∞時可得
uN→u在L∞(0,T;H1(Ω))中弱收斂,uN→u在L2(0,T;H2(Ω))中弱收斂;
uN→u在L2(0,T;L2(Ω))中幾乎處處成立;
uN→u在L4q+4(0,T;L4q+4(Ω))中弱收斂;

線性部分的估計可以直接得到,然后考慮非線性項,根據勒貝格控制收斂定理,再由先驗估計已知f(uN)在L2(0,T;L2(Ω))中一致有界,則可以得到f(uN)在L2(0,T;L2(Ω))中收斂于f(u).同樣由于先驗估計(16)式可得g(uN)在L∞(0,T;L2(Ω))?L2(0,T;L2(Ω))中一致有界,則g(uN)在L2(0,T;L2(Ω))中收斂于g(u),則解的存在性得證.
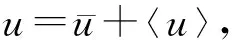
〈f(u1)-f(u2)〉+(-Δ)-1(g(u1)-
g(u2)-〈g(u1)-g(u2)〉)=0,
(42)
在Ω對方程(1)~(3)積分可得
(43)

f(u2),u))-((f(u1)-f(u2),〈u〉))+
(((-Δ)-1(g(u1)-g(u2)-
(44)
其中
((f(u1)-f(u2),u))≥-c0‖u‖2≥
因此
|((f(u1)-f(u2),〈u〉))|≤
同樣
|((g(u1)-g(u2)-〈g(u1)-g(u2)〉,
將〈u〉與(43)式做內積可得
根據(44)~(45)式,運用插值不等式‖u‖2≤‖▽u‖‖u‖-1可得
根據Gronwall引理可得
‖u1(t)-u2(t)‖-1≤c‖u1,0-u2,0‖-1,c>0,t∈[0,T].
由此可知u1(t)=u2(t),則解的唯一性得證.
定理 2.1關于方程(1)~(3)的解u滿足
?r
證明方程(13)可寫成如下形式
(46)
將(46)式對時間求偏導可得
(47)
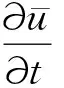
其中根據假設(8)和連續嵌入H2(Ω)?L∞(Ω)有
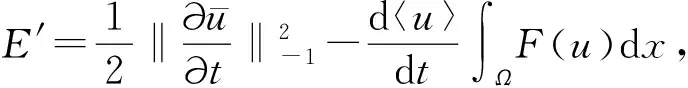
根據插值不等式可得
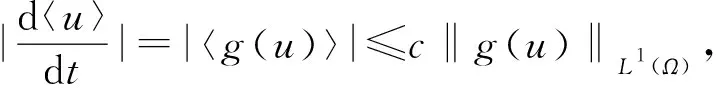
同時還可以得到(48)式右邊兩項是有上界的.最后根據Gronwall引理可得
?r

