基于波利亞提示語優化教學的案例分析

酆京亞　彭慧

［摘 要］烙餅問題是小學生體會優化思想的經典問題。烙餅問題引導學生不僅要解決問題，而且還要高效地解決問題。這與波利亞“怎樣解題”表所提出的問題不謀而合，可通過設置“提示語”“引導性問題”，幫助學生初步形成從數學的角度提出問題、分析問題、解決問題的能力，在烙餅問題的解決過程中體會優化思想。

［關鍵詞］波利亞提示語；問題序列；烙餅問題；優化

［中圖分類號］ G623.5［文獻標識碼］ A［文章編號］ 1007-9068（2024）08-0055-04

《義務教育數學課程標準（2022年版）》要求義務教育階段的學生發現問題和提出問題，運用數學和其他學科的知識與方法分析問題和解決問題。南京師范大學數學與計算機科學學院教授、博士生導師涂榮豹認為，數學解題元認知能力的提高有賴于解題者善于運用波利亞的提示語以及善于提煉具有個人風格的提示語。李懷軍、張維忠在研究中發現，小學生的數學問題提出能力不強，且小學生數學問題提出能力的發展存在階段性，四年級為發展這一能力的“關鍵期”。

一、基于波利亞提示語的“烙餅問題”教學目標定位及內容安排

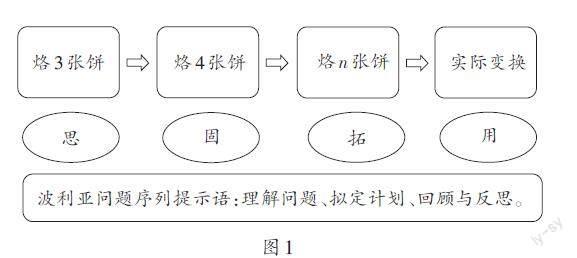
優化思想在解決問題的策略中發揮著重要作用，人教版教材中多次滲透優化思想，如搭配問題、沏茶問題、烙餅問題、田忌賽馬、找次品等。在低學段中，學生對優化思想有了一定的感悟，在進入高學段后，學生初步體會解決問題方法的多樣性，在“多”中擇“優”，將“做”和“思”有機結合，初步形成提出問題、分析問題、解決問題的能力。烙餅問題從烙3張餅、4張餅、10張餅……[n]張餅，是滲透優化思想的一個重要載體，同時也是問題的遷移和拓展。對此，筆者認為教學最核心的要素是讓學生體會到“最快”的思想本質，也就是鍋里總是烙2張餅，給學生探索的空間，體悟根據餅的張數分奇偶的情況分析。基于波利亞提示語的烙餅問題教學思路如圖1所示。

二、波利亞提示語在“烙餅問題”教學中的案例分析

出示“烙餅問題”情境1：爸爸、媽媽和我每人吃1張餅，但是鍋里每次最多只能烙2張餅，兩面都要烙，每面烙3分鐘，怎樣才能盡快吃上餅？

1.提示語序列串：理解問題

師：首先想一想，我們要完成的事情是什么？

生1：要烙3張餅。

師：只是烙3張餅嗎？還有沒有其他的要求？

生2：盡快吃上餅。

師：“盡快”怎么理解呢？

生3：就是用最短的時間去烙好3張餅。

師：我們需要烙好3張餅，同時要用時最短。接下來我們看看，已知條件告訴了我們什么信息？

生4：1張餅要烙兩面，每面烙3分鐘。

師：還有其他信息嗎？

生5：每次最多只能烙2張餅。

師：怎么理解“每次最多只能烙2張餅”呢？

（教師拿出自制教具：1個“鍋”、3張“餅”）

生6：鍋里每次只能放2張餅。

師：可不可以在鍋里只放1張餅呢？

生7：可以。

師：那鍋里既可以放1張餅，也可以同時放2張餅，你會怎么選擇呢？說說你為什么這樣選擇。

生8：我選同時放2張餅，因為這樣更快，也節省時間。

2.提示語序列串：擬定計劃

師：那烙2張餅需要多長時間呢？

生9：12分鐘。因為烙1張餅需要6分鐘，所以烙2張餅需要12分鐘。

生10：6分鐘。因為一個鍋里可以同時放2張餅，每面烙3分鐘，兩面只需要6分鐘。

師：我們整理一下，“每次烙（）張餅，別讓鍋（）”，這樣應該最省時間。那烙3張餅最少需要多長時間呢？

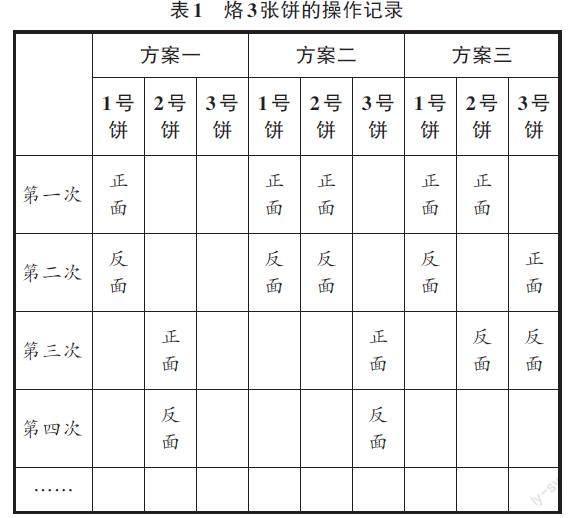
設置比賽，模擬計時，讓每個學生都動手操作，借助教具圓片來“烙”，并記錄烙餅方案（見表1）。

生11：方案一1張1張烙用時最長，需要18分鐘；方案二先2張同時烙，再單獨烙1張，這樣最后1張只能先烙正面，再烙反面，需要12分鐘。

師：我們需要烙3張餅，每張餅需要烙2面，一共需要烙多少面？

生12：要烙6面。

師：每次鍋里可以烙2面，那是不是3次就可以把這6面烙完呢？

生13：是呀，3次就可以了。

生14：鍋里是不能空著，要同時烙2張餅，我們要烙3張餅，可以按照方案三交替烙的方法，第一次烙1號餅、2號餅的正面，第二次烙1號餅的反面、3號餅的正面，第三次烙2號餅、3號餅的反面，一共需要9分鐘。

3.提示語序列串：回顧與反思

師：我們成功解決了這個問題。我們是怎么解決這個問題的呢？關鍵是什么？

生15：不能讓鍋空著。

生16：交替烙。

師：能不能把這個方法用于其他的問題？

4.教學評析

烙3張餅是本次教學活動的基礎，學生會有不同層次的表征。基于層層遞進的問題序列串，引導學生明確情境中的信息，借助直觀教具“鍋”“餅”，讓學生體悟優化思想。

出示“烙餅問題”情境2：爸爸、媽媽、姐姐和我每人吃1張餅，但是鍋里每次最多只能烙2張餅，兩面都要烙，每面烙3分鐘，怎樣才能盡快吃上餅？

1.提示語序列串：理解問題

師：按照剛才的思路，我們要完成的事情是什么？已知條件告訴了我們什么信息？

生17：烙4張餅最快需要多長時間。

生18：鍋里最多同時烙2張餅，每張餅要烙兩面，每面烙3分鐘。

生19：不能讓鍋空著。

2.提示語序列串：擬定計劃

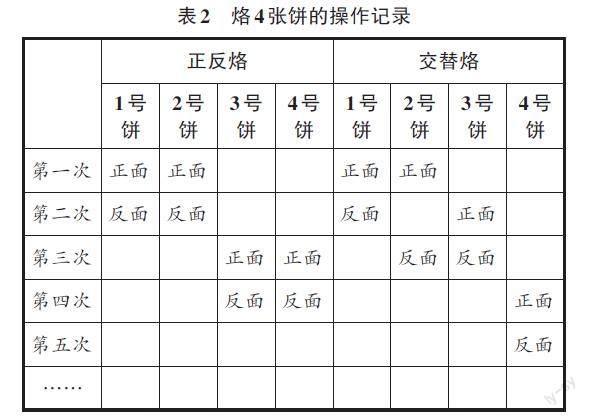
引導學生拿出學具，動手試一試，并記錄烙餅方案（見表2）。

師：哪種烙法更快？

生20：正反烙。

師：為什么正反烙更快？

生21：正反烙只需要烙4次，而交替烙則需要烙5次。

生22：因為有4張餅，交替烙3張后，還多1張餅，這多的1張只能一面一面地烙，浪費了時間。

師：2張餅正反烙更快，3張餅交替烙更快，4張餅正反烙更快。那么烙5張餅用哪種方式更快呢？其中有沒有規律呢？

引導學生借助學具進行猜想，并記錄烙餅方案（見表3）。

師：烙5張餅有哪些方法，哪種方法更快？

生23：先交替烙3張，再正反烙2張。

生24：先正反烙2張，再交替烙3張。

師：你發現了什么規律？你能將發現的規律整理成表格的形式嗎？

學生利用規律進行驗證，并記錄烙餅方案（見表4）。

3.提示語序列串：回顧與反思

師：烙雙數張餅時，選擇什么方法更快？烙單數張餅呢？

生25：烙雙數張餅時，2張2張正反烙更快。

生26：烙單數張餅時，先2張2張正反烙，剩下3張再交替烙。

出示情境3：一個餐廳里同時來了3位客人，每人點了2道菜，這6道菜各不相同，而餐廳里只有2個廚師。假設2個廚師炒每個菜的時間相等，為了讓每個顧客都盡快吃上飯，應該按怎樣的順序炒菜？

生27：第一次，2個廚師給1號客人和2號客人各做1道菜；第二次，2個廚師給1號客人和3號客人各做1道菜；第三次，2個廚師給2號客人和3號客人各做1道菜。

師：說得非常好。掌握了優化方法，我們就可以更好地解決生活中的很多問題。解決問題的方法多種多樣，我們要用數學的眼光去看待問題，合理安排，以尋找解決問題的最優方案。

（課后思考：如果每面需要烙5分鐘，烙3張餅最快需要多長時間？）

4.教學評析

在烙3張餅的基礎上，進一步探索烙4張餅、5張餅……怎樣安排最省時，借助學具操作實踐交替烙、正反烙，體悟其中規律：無論烙餅的數量是多少，都可以分解成多個2的和或多個2與3的和；如果烙餅張數是雙數，可以正反烙，如果烙餅張數是單數，則先正反烙，最后3張餅交替烙。最后基于生活情境，感受數學生活化。

三、教學反思

（一）教學設計以波利亞問題序列進行串聯

通過一系列具有個人特色的問題序列串的設計與實施，按照波利亞的解題四步問題序列：①理解問題，需要解決的問題是什么？已知條件有哪些？這些條件的作用是什么？（讓學生初步感知最多只能烙2張餅時，烙2張餅的時間與烙1張餅的時間相同）；②擬定計劃，你能利用這些條件解決問題嗎？是否利用了所有的已知條件？有沒有遺漏？有沒有曾經做過類似但是簡單一些的問題？（讓學生把烙3張餅的問題先簡化為烙2張餅，明確每次都烙2張餅，別讓鍋空著的省時烙法）；③實施計劃，一步一步去實現計劃，注意每一步保持正確；④回顧與反思，能否用其他方法獲得這個結果？能否把這個結果用在其他問題上？

（二）在問題序列中體會優化思想

不斷設置引導性提示語，抓住幾個關鍵問題：怎樣更快？鍋空著會怎樣？什么時候選擇正反烙？什么時候選擇交替烙？一切的核心是讓學生體悟到“最快”“省時”，也就是鍋里總是同時烙2張餅最省時（優化思想）。再進一步探索，如果烙4張餅、5張餅……怎樣安排最省時間？通過引導，學生總結出如果餅的張數是雙數，2張2張正反烙更快；如果餅的張數是單數，先2張2張正反烙，最后3張餅交替烙更快。波利亞提示語留給學生充足的自主探索空間，這有助于學生深刻體會優化思想。

（三）在課堂探究中突顯直觀優勢

以真實的生活情境，引發學生探究的欲望：課前準備學具——1個“鍋”、3張“餅”，讓學生親身經歷烙餅的過程；人教版教材中出示的圖表，展現了烙3張餅的具體操作過程，這些都突顯了直觀優勢，有利于學生理解和體會數學思想。學生由具體到抽象，由操作到擺脫學具，循序漸進、層層深入，探究出烙餅張數與所用最短時間之間的關系，提升了他們的思維，讓他們獲得最優的烙餅方法。

（四）在拓展應用中發散思維

從特殊情況開始，先烙2張餅、烙3張餅，到烙4張餅、5張餅……10張餅，再到n張餅，這是烙餅問題的拓展和遷移，再出示情境3讓學生進行鞏固應用，思考做6道菜的先后順序，讓學生體會數學的靈活性以及感受到數學具有的生活性，從而達到發散學生思維的目的。

［ 參 考 文 獻 ］

[1] 涂榮豹.數學解題學習中的元認知[J].數學教育學報，2002（4）：6-11.

[2] 李懷軍，張維忠.小學生數學問題提出能力發展研究[J].數學教育學報，2019，28（5）：2-8.

[3] 張衛星.研讀數學教材的四個維度：以人教版數學四年級上冊“烙餅問題”為例[J].教學與管理，2015（14）：35-37.

[4] 張小燕.讓學生觸摸問題的本質：“烙餅問題”的教學重構與思考[J].教育科研論壇，2011（3）：43-44.

【本文系2021年江西省高等學校教學改革研究課題“基于OBE理念的波利亞解題思想在《概率統計》教學中的應用研究”研究成果（課題編號JXJG21-23-14）。】

（責編 覃小慧）