一種基于聲波信號的室內定位方法?

吳修振 馮慧鳳 孫 燁 祁亞輝 閆 實

（1.海軍航空大學 煙臺 264000）（2.91428部隊 寧波 315456）

1 引言

在當今人們的生活中，定位技術無處不在。在室外，人們通過GPS、北斗等室外定位技術來獲得準確位置信息，實現汽車、人員導航。而近幾年，隨著物聯網產業的發展，室內定位也逐漸成為剛需，尤其對于室內機器人應用來講，首要解決的問題就是機器人的定位問題。

目前常見的室內移動機器人定位技術有光跟蹤定位技術、藍牙定位技術、RFID 定位技術、WiFi定位技術等［1～7］。其中光跟蹤技術要求探測器和跟蹤目標之間可視，故而光跟蹤技術的應用受限；藍牙技術所需的設備體積小，易于集成在PDA、PC 以及手機中，但它在復雜的環境中穩定性差，覆蓋范圍小；RFID 定位技術即射頻識別技術，是一種無需直接接觸地識別技術，具有非視距傳輸、識別速度快等特點，但是其通信能力較弱，定位誤差大，系統部署復雜，容易受到環境影響等；WiFi 定位可以實現復雜的大范圍定位，方便組網，很容易架設在現有的無線WiFi 網絡，但WiFi 定位存在同頻干擾問題，系統會相互影響。

針對室內機器人的定位問題，本文提出了一種基于聲波信號的室內定位方法，核心設備為麥克風、聲源以及單片機數據處理系統，特點是成本低，具有一定的應用前景。基于聲波信號的室內定位方法基本原理是：當同一個聲源發出特定聲音信號時，聲音信號會在空氣中按照聲速沿著各個方向進行傳播，安裝在不同位置的麥克風傳感器接收到這個聲音信號，不同麥克風接收的聲音信號必然存在著相關性。因此，通過計算不同的麥克風在接收到同一個聲源的聲音信號之間的相關系數，就可以得出聲音信號到達麥克風的時間差，有了時間差就有了距離信息［8～12］。

本文首先推導基于快速傅里葉變換FFT（Fast Fourier Transform）求解兩個信號相關系數的原理，然后闡述利用互相關系數確定聲源方位和位置的具體實現方法，最后對FFT求解互相關系數的過程進行了仿真，并搭建單片機系統對提出的基于聲波信號的室內定位方法進行實現。

2 基于FFT求解廣義互相關系數

假設聲源發出的Chrip 信號為s(t)，兩個麥克風接收到的信號分別為x1(t)和x2(t)。則信號x1(t)和x2(t)滿足：

其中，S1和S2是發射信號的幅度參量，n1(t) 和n2(t)是噪聲信號，τ1和τ2是信號傳輸的時延，并且τ1≤τ2，以x1(t)為標準進行歸一化，式（1）可以轉換為

對式（2）進行離散變換為

其中，λ=S1S2，D=τ2-τ1，前者表示兩個信號的幅值之比，后者表示所求得時延值。x1(t)和x2(t)的互相關函數為

假設n1(t)和n2(t)是獨立于信源發射信號s(t)的高斯白噪聲，且互不相關，則信號s(t)與兩個噪聲n1(t)和n2(t)的互相關函數是：

兩個噪聲之間的互相關函數是：

由自相關函數|Rss(τ) |≤Rss(0) 的主要特征和基本性質我們可以得知，當τ=D時，Rss(τ-D)最大，即R12(τ) 也達到最大。因此，求得R12(τ)峰值對應的τ，就是兩個接收信號之間的諧波頻率和信號時延。

根據維納—辛欽定理可知，互相關函數與其互功率譜密度互為傅里葉變換對，則x2(t)和x1(t)的互相關函數又可以表示為

其中，G12(ω)是x1(t)和x2(t)的互功率譜函數。當x1(t)和x2(t)經過濾波后，輸出信號的互功率譜函數可以寫為

其中，H1和H2表示濾波函數，H2*(ω)表示H2(ω)取共軛。所以，信號x1(t)和x2(t)的廣義互相關函數可表示為

其中，Ψ12（ω）代表了廣義頻域的加權分量。

廣義互相關時延估計算法流程，如圖1 所示，圖中（）*表示取共軛運算。

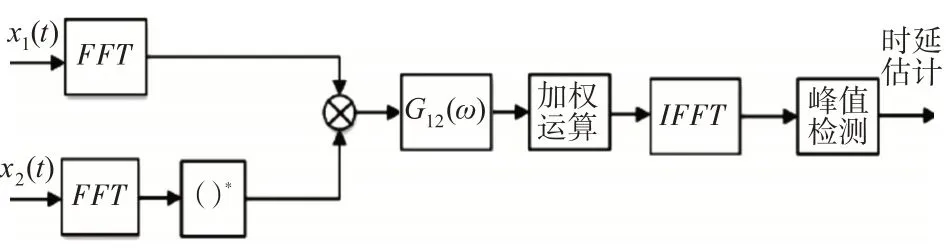
圖1 廣義互相關時延估計算法流程

在基于廣義互相關時延估計的算法工作流程中，先對兩個頻段之間的接受信號分別做一個快速傅里葉變換FFT（Fast Fourier Transform），然后計算它們的互相關功率譜，在頻域上對接受信號的互相關功率譜G12（ω）函數進行加權運算，然后進行逆快速傅里葉變換IFFT，最后進行峰值檢測，求得兩個麥克風檢測到的聲音信號的時間差，也就得到了兩個麥克風到聲源的距離差。

3 基于互相關系數求解位置和方位

如圖2 所示，建立平面直角坐標系OXY，4 個麥克風編號①②③④，以固定間距成正方形分布，以坐標軸OX、OY 以及四個麥克風對角連線，可將平面劃分成八個象限，順時針依次為+1、+2、+3、+4、-4、-3、-2、-1。

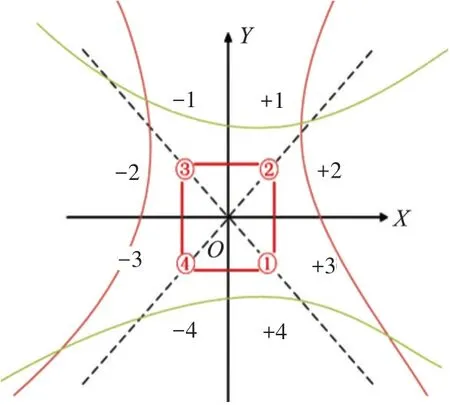
圖2 定位示意圖

用max12 表示①號麥克風接收到的聲波信號和②號麥克風接收到的聲波信號通過互相關計算得到的采樣周期差。max12 的正負可以確定聲源位于OX 軸的上方還是下方，如果為正，聲源位于OX軸的上方，如果為負，聲源位于OX軸的下方，這樣，通過兩個麥克風信號的互相關系數可以把聲源的方位劃分為兩個象限，同理，再通過max23、max13、max24可以把聲源劃分為八個象限。

確定了聲源的方位以后，下一步就是確定聲源的位置。通過max12 和信號采樣頻率就可得到聲源距離①號和②號麥克風的距離，距離兩個定點一定距離的軌跡是雙曲線，聲源一定在雙曲線上，因此通過max12可以確定聲源的一個雙曲線軌跡（圖2綠色軌跡），再通過max23的值又可以確定一個聲源的雙曲線軌跡（圖2 紅色軌跡），兩個雙曲線相交可得到四個交點，通過前面得到的聲源的象限可以確定這四個交點哪一個代表了聲源的位置，通過求取交點的坐標就可以得到聲源相對麥克風的位置坐標，根據坐標相對性原理，有了聲源的位置坐標，就可以得到麥克風相對聲源的位置坐標。

坐標定位精度與麥克風采樣頻率有關，假設采樣頻率是10kHz，聲速為340m/s，則一個周期代表的距離是3.4cm，即麥克風測量的分辨率為3.4cm，那么定位精度也為3.4cm。

4 仿真與試驗驗證

4.1 仿真驗證

用Matlab 以采樣頻率10kHz、幅值為1 生成兩個Chrip 信號，如圖3 所示，兩個Chrip 信號相差的周期數為800。

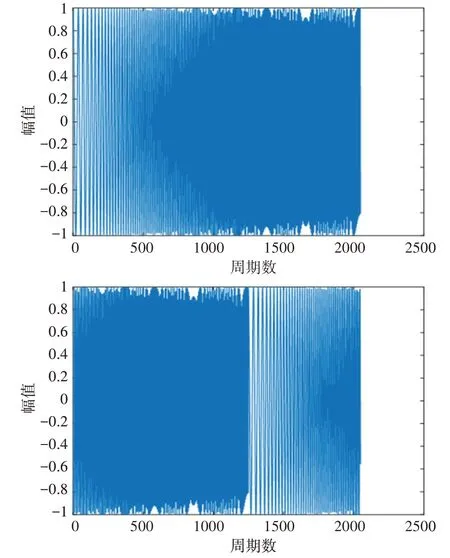
圖3 chrip信號

利用快速傅利葉變換FFT 求解兩個Chrip 信號的互相關系數，如圖4所示。

通過圖4 可知，當周期數為800 時，兩個Chrip信號的互相關系數達到最大值，即兩個信號相差800 個采樣周期，這與生成信號時的設定是吻合的，通過仿真結果可知，利用FFT 求解兩個信號的互相關系數是可行的。

4.2 實驗驗證

4.2.1 試驗設備

搭建單片機系統基于C 語言實現提出的基于聲波信號的定位方法，搭建的單片機主板PCB如圖5所示。

四個麥克風的布局如圖6所示。

圖6 麥克風布局

4.2.2 試驗過程

Step1：對實驗系統進行搭建，選用四個麥克風，進行編號①②③④，與PCB板相連，然后通過支架將它們固定成一個正方形，每組兩個麥克風之間的距離是25cm，見圖6，選用的聲源是聲波發生器，可以持續不斷的發出Chrip聲音信號。

Step2：啟動聲波發生器，運行單片機程序在線進行調試，采集四個麥克風的聲波信號數據，進行AD 轉換，然后通過快速傅利葉變換FFT 求解四組互相關系數max12、max23、max13、max24，依據互相關系數確定聲源的象限，對比麥克風與聲源實際的位置關系，判斷單片機輸出的象限結果是否正確，并且輸出聲源的位置坐標。

Step3：通過平移和旋轉改變麥克風陣列的位置，多次記錄單片機的輸出結果。

Step4：統計數據，得到最終的實驗結果。

4.2.3 實驗結果

實驗過程中數據顯示的界面如圖7所示。

圖7 數據顯示界面

將麥克風陣列沿順時針繞聲源進行旋轉，多次繞圈100 次，理論上是每個象限出現的次數是一樣的，在實驗次數足夠多的情況下，各個象限出現的次數應該都是12.5%左右。將每一次象限變化的數值以及定位信息都記錄下來，結果如表1所示。

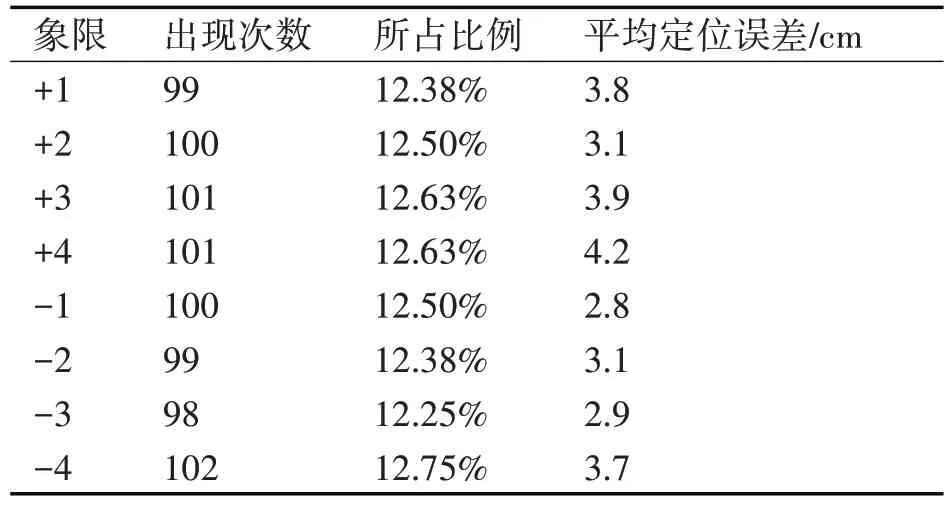
表1 實驗數據

通過表1 可知，每個象限出現的概率基本為八分之一，象限的確定是準確的，因此利用聲波信號進行定位時聲源的方位信息可以準確得到。定位精度也達到了設計要求，定位精度在3.4cm 左右，與理論分析一致。

5 結語

通過仿真和實驗驗證，本文設計的基于聲波信號的室內定位方法有效可行，達到了厘米級的定位精度，有效解決了室內移動機器人的定位問題，該方法已成功應用在全國大學生智能車競賽中，取得了良好的效果。從實驗和具體應用過程來看，由于環境中噪聲的干擾，基于聲波信號的定位方法的穩定性和魯棒性還需要進一步提高和優化。