基于優勢關系粗糙集的導彈保障器材運輸決策模型?

單 鑫 孫 媛 王

（1.海軍航空大學 煙臺 264001）（2.91550部隊 大連 116040）

1 引言

戰時導彈保障器材運輸路徑優化，也是導彈裝備供應保障的主要任務之一。在現代戰爭中，由于高技術武器的不斷涌現和介入，作戰進程空前加快，呈現高度復雜和瞬息萬變的局面，各類信息的定量工作難度越來越大，戰時導彈保障器材運輸路徑決策具有目標多樣化和決策信息不確定性等諸多特點，經典運籌學中用于運輸路徑優化的方法已很難再適應戰時運輸路徑決策的需求。而目前，在相關部門在日常工作計劃和制定的有關戰時導彈保障器材運輸保障預案中，對運輸路徑的決策方式主要還是依靠經驗作定性或半定量的分析，還沒有很好地反映戰時運輸的特點和找到解決路徑優化問題的有效方法。因此，有必要對戰時導彈保障器材運輸路徑優化問題進行研究。對一些不確定信息，人們通常難以用精確數值來描述，卻往往能給出信息的上界和下界，這類信息可采用區間數來描述。同時，模糊信息也可區間數來描述，如區間模糊數。因此，文章主要研究在區間信息下建立能夠反映戰時導彈保障器材運輸特點的路徑優化模型。

2 問題描述

戰時導彈保障器材運輸路徑優化問題是一個典型的多目標決策問題。但在導彈保障器材實際運輸活動中，受各種條件制約，備選可行路徑是有限條的。因此，戰時導彈保障器材運輸優化問題是一個有限方案的多目標（屬性）決策問題，問題描述如下：

設有決策信息系統S=(U,A,V,f)，其中，U={x1,x2,…,xn} 為非空的有限集合，分別對應于n條備選路徑；A 為非空的屬性集，A=C∪D，C={a1,a2,...,am}是一個非空、有限的條件屬性集合，對應于m個路徑優化相關屬性，｛d｝為決策屬性集，屬性值V=Vc∪Vd，其中Vc條件屬性值集，Vd決策屬性值集，并且條件屬性值和決策屬性值有偏好次序；f:U×Q→V是一個信息函數，表示對每一個α?A，x?U,f(x,a)?Va，由于戰時信息的不確定性，部分屬性值往往只能以區間數的形式給出，故f(x,a) 為區間數，f(x,a)=[aL(x),aU(x)]={p|aL(x)≤p≤aU(x),aL(x),aU(x)?R}。顯然這是一個有偏好信息的多屬性決策表。現要在備選路徑集中選擇一條或多條合適的路徑作為戰時導彈保障器材運輸路徑。

3 保障器材運輸路徑影響因素分析

在作戰條件下，導彈保障器材運輸路徑的選擇除了必須考慮滿足時間目標外，還需要考慮導彈保障器材在運輸過程中的影響因素。具體如圖1所示。

圖1 戰時導彈保障器材運輸路徑優化影響因素

4 優勢度優勢關系下的區間序粗糙集

4.1 原有優勢關系的局限性分析

關于屬性值具有偏好關系的區間值信息系統的粗糙集方法的研究已有很多報導［1～3］。對文獻［1～3］中定義的幾種優勢關系進行分析，可以發現這幾種優勢關系存在著一定的缺陷，具體如下：

從以上分析可知，當前區間序信息系統上的幾種優勢關系存在定義過寬或過窄的問題，過窄則導致分類中的信息過少，而過寬則會導致分類中產生不合理的結果。因此，下面提出了一種新的優勢關系。

4.2 α-優勢度優勢關系

4.2.1 區間序信息系統的優勢度

定義1對區間序信息系統S=(U,A,V,f)，對任意xi,xj?U，a?A，記f(xi,a)=[aL(xi),aU(xi)]，f(xj,a)=[aL(xj),aU(xj)]，有

定義2稱為允許優勢度。若αji=1，則對象xj一定優于xi，若αji=0，則對象xj一定不優于xi；若0<αji<1，則對象xj可能優于xi。

進一步地，對給定優勢度α，若αji≤α，則認為在優勢度α下，存在屬性a?A，使得對象xj不優于xi。若αji≥α，則對給定優勢度α，A 中不存在任何屬性使得對象xj不優于xi。在這種情況下，本文認為在優勢度α下，對象xj優于xi。若對象xj優于xi，則應滿足，由互補性可知，則。因此，為了保證分類的準確性，α?[0.5,1]。由此，可給出α-優勢度優勢關系的定義。

4.2.2 α-優勢度優勢關系

定義3設區間序信息系統S=(U,A,V,f)，B?A，B=B1∪B2，其中B1為效益型屬性集，B2為成本型屬性集。給定優勢度α?[0.5,1]，則可定義α-優勢度優勢關系和α-優勢類：

在區間序信息系統中引入優勢度α后，可以通過閾值α?[0,1]變化來調節優勢關系的“優于”程度，這樣就提高了信息處理的靈活性。可以驗證，α-優勢度優勢關系通過對“優于”程度的定義，能夠克服文獻［1～4］中五種優勢關系的不足。

4.3 基于α-優勢度優勢關系的區間序粗糙集擴展模型

定義4設區間序信息系統S=(U,A,V,f)，對給定的優勢度α?[0.5,1]，對任意B?A，X?U，關于的上下近似定義如下：

邊界域的存在引起了集合中的不確定性。集合的邊界域越大，其精確性越小。為了描述粗糙集在α-優勢度優勢關系下的不精確性，下面給出近似精度的定義。

定義5設區間序信息系統S=(U,A,V,f)，X?U，B?A，α?[0.5,1]，定義X關于優勢關系的近似精度：

4.4 區間序決策信息系統的優勢規則

參考文獻［4］中對不完備序信息系統上決策規則進行描述。對區間信息系統S=(U,A,V,f)，A={a1,a2,...,am}，其中a1,a2,...,ak為效益型屬性，ak+1,ak+2,...,am為成本型屬性，在優勢關系R≥Bα下的兩種優勢規則可描述如下：

1）確定型優勢規則

對給定優勢度α?[0.5,1]，若(f(x,a1)≥αva1)?(f(x,a2)≥αva2)?…(f(x,ak) ?(f(x,ak+1)≤1-αvak+1)?(f(x,ak+2)≤1-αvak+2)?…(f(x,am)≤1-αvam)，則。

2）可能型優勢規則

對給定優勢度α?[0.5,1]，若(f(x,a1)≥αva1)?(f(x,a2)≥αva2)?…(f(x,am) ?(f(x,ak+1)≤1-αvak+1)?(f(x,ak+2)≤1-αvak+2)?…(f(x,am)≤1-αvam)，則x 可能屬于。

其中f(x,ak)≥αvak表示對區間數f(x,ak) 對vak的優勢度。f(x,ak)≤1-αvak表示f(x,ak)對vak的優勢度。

4.5 區間序決策信息系統的屬性約簡

為了獲取區間序決策信息系統上更為簡潔的決策規則，就需要對決策信息系統進行屬性約簡。區間序決策信息系統可分為協調決策信息系統和不協調決策信息系統，具體含義如下：

定義6設區間序決策信息系統S=(U,C∪d,V,f)，d為決策屬性，其中決策屬性值Vd是有序的：

給定α?[0.5,1]，若，則稱S 是協調的，否則稱S是不協調的。

定義7設區間序決策信息系統S=(U,C∪d,V,f)是協調的，B?C，給定α?[0.5,1]。

則稱B為區間序決策信息系統上的一個α－相對約簡集。

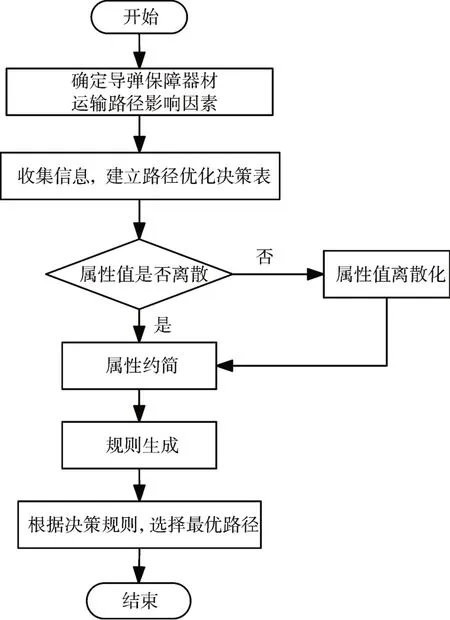
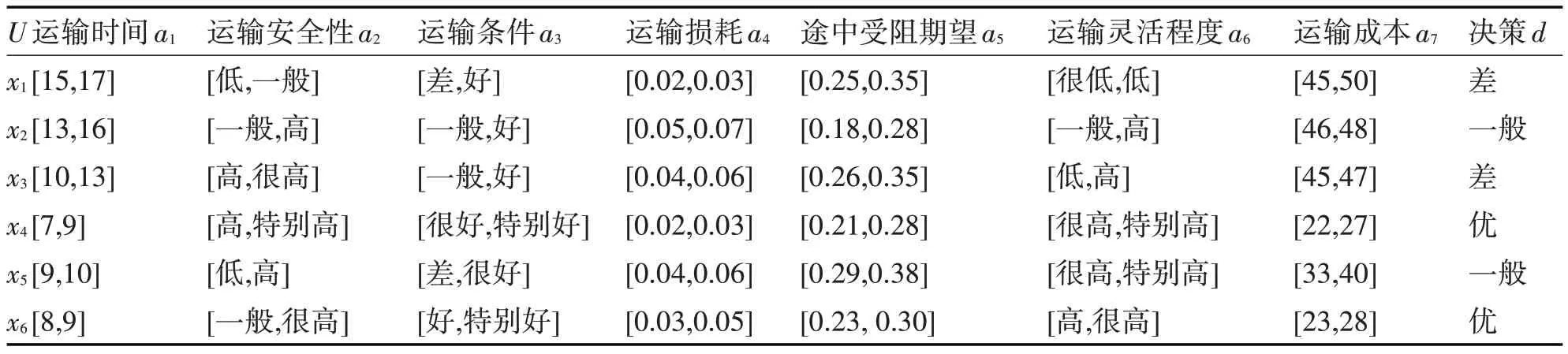
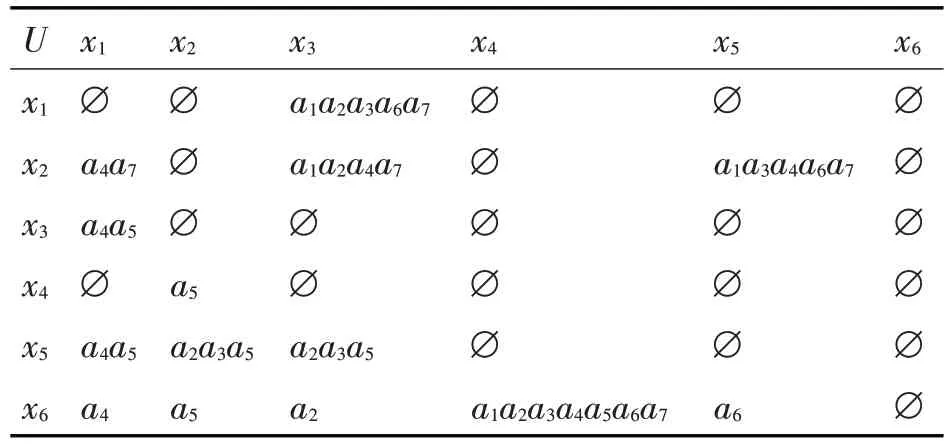
下面采用差別函數方法來研究協調的區間序決策信息系統上的屬性約簡集。令D*={(xi,xj)|f(xi,d)

現引入一個布爾函數ΣδA(xi,xj)，對給定α?[0.5,1]，令

對布爾函數ΣδA(xi,xj)，若δA(xi,xj)=?，則布爾函數為1；否則ΣδA(xi,xj)為δA(xi,xj)所包含的屬性的對應變量的析取。因此差別函數可定義如下：

Δ 為區間序決策信息系統S=(U,A,V,f)上的差別函數，當且僅當

應用布爾代數中的分配定律和吸收定律對差別函數對差別函數化簡，得到函數Δ 的極小析取范式，從而可求得區間序決策信息系統的α－相對約簡。

5 戰時導彈保障器材運輸路徑優化模型的建立

戰時導彈保障器材運輸路徑優化模型程序流程如圖2所示。

圖2 戰時導彈保障器材運輸路徑優化模型流程圖

5.1 區間序決策信息表的建立

由定義1，以導彈保障器材運輸路徑影響因素作為條件屬性，路徑的優劣程度作為決策屬性，可建立戰時運輸路徑優化決策信息表S=(U,C∪g0gggggg,V,f)，其形式如表1 所示。其中，C=｛a1，a2，a3，a4，a5，a6，a7｝為條件屬性集：a1-運輸時間，a2-運輸的安全性，a3-運輸條件，a4-運輸的途中損耗，a5-運輸的途中受阻期望，a6-運輸的靈活程度，a7-運輸成本。“d”為決策屬性。F={fl:U→Vl(l≤m)}，fl(xi)表示方案xi關于屬性al的值。

表1 戰時導彈保障器材運輸路徑優化決策信息表

5.2 屬性約簡

區間序決策信息系統S=(U,C∪g0gggggg,V,f)屬性約簡算法描述如下：

輸入：區間序決策信息系統S=(U,C∪g0gggggg,V,f)

輸出：α-相對約簡集B

Step1：給定優勢度α，根據定義4，求條件屬性α-優勢類；

Step2：求D*={(xi,xj)|f(xi,d)

Step3：由式（6），可求得差別矩陣δA(xi,xj)；

Step4：重復Step 3，可得到所有差別矩陣元素，由式（7）計算區間序決策系統S的差別函數；

Step6：令Bk={ats:s=1,2,…qk}(k=1,2,…,t)，由Step5分別得到，｛Bk:k=1,2,…,t｝，即為區間序決策信息系統的α-相對約簡集。

5.3 決策規則生成

通過屬性約簡，從而獲取最簡決策規則集，可為戰時導彈保障器材運輸路徑選擇提供依據。決策規則獲取的具體步驟如下。

Step1：求出對象上下近似和邊界域，從而得到確定型和可能型優勢規則；

Step2：根據得到屬性約簡集，去除優勢規則中的冗余屬性；

Step3：對得到的規則的條件部分和決策部分進行合并，并去除重復的規則。

5.4 算例

為滿足導彈器材供應保障需要，需要從某導彈倉庫向保障陣地運輸導彈保障器材，現要選擇合適的運輸路徑。

1）決策信息表的建立

從通過收集歷次演習數據以及邀請專家討論等方式，可得到導彈保障器材運輸路徑優化決策信息表（如表2所示）。

表2 導彈保障器材運輸路徑優化決策信息表

為便于計算，對模糊屬性量化如下：特別低為1、很低為2、低為3、一般為4、高為5、很高為6、特別高為7。對決策d：差為1，一般為2，優為3，則可得到戰時導彈保障器材運輸路徑優化決策信息表。顯然，此時得到的表為區間序信息表，條件屬性中運輸時間a1、運輸損耗a4、途中受阻期望a5、運輸成本a7為成本型屬性，其余為效益型屬性。

2）屬性約簡

按照區間序決策信息系統屬性約簡方法求區間序決策信息系統的α-相對約簡集。取α=0.75，則

決策屬性d對U構成劃分D={D1,D2,D3}，

表3 差別矩陣

然后，可得到區間序信息表的差別矩陣，如表3所示。

由表3，可得到差別函數：

即區間序決策信息系統的α-相對約簡集為B=｛a2，a4，a5，a6｝。于是，可得到如下確定型優勢規則：

r1：(f(x,a2)≥0.75[4,6]) ? (f(x,a4)≤0.25[0.03,0.05]) ? (f(x,a5)≤0.25[0.23,0.30]) ? (f(x,a6)≥0.75[5,6])，則d≥3（對象x4，x6支持）。

r2：(f(x,a2)≥0.75[4,5]) ? (f(x,a4)≤0.25[0.05,0.07]) ? (f(x,a5)≤0.25[0.18,0.28]) ? (f(x,a6)≥0.75[4,5])，則d≥2（對象x2支持）。

r3：(f(x,a2)≥0.75[3,5]) ? (f(x,a4)≤0.25[0.04,0.06]) ?(f(x,a5)≤0.25[0.29,0.38]) ?(f(x,a6)≥0.75[6,7])，則d≥2（對象x4，x5支持）。

3）利用獲取的優勢規則，對備選路徑進行優選

從某導彈倉庫到保障陣地的備選路徑有4 條，其基本信息如表4所示。

表4 備選路徑基本信息

將備選路徑信息與規則對比，僅有路徑C 滿足：

運輸安全性(f(x,a2)≥0.75[4,6])，且運輸損耗(f(x,a4)≤0.25[0.03,0.05])，且途中受阻期望(f(x,a5)≤0.25[0.23,0.30])，且運輸靈活程度(f(x,a6)≥0.75[5,6])。

則由規則r1可知，路經C為“優”，因此選擇C作為運輸路徑。將路徑C 與其它路徑相比，C 的各項屬性取值均處于較高水平，結論基本合理。因此，本文的方法是有效的。

6 結語

本文針對戰時導彈保障器材運輸路徑優化不確定問題，提出了一種基于優勢度的優勢關系—α-優勢度優勢關系，定義了基于α-優勢度優勢關系的擴展粗糙集模型。采用基于差別函數的屬性約簡算法，簡化了區間序信息系統，得到了更為簡潔的優勢規則。在此基礎上建立了戰時導彈保障器材運輸路徑優化模型，這為戰時導彈保障器材運輸路徑優化等區間值信息系統上的決策分析提供了一種新的方法。而基于差別矩陣的屬性約簡算法僅適用于屬性數量較少的情況，而當屬性數量足夠大時，屬性約簡就變成了NP-Hard 問題，該方法則難以求解，需要進一步完善本文提出的模型和方法，進一步加強導彈器材供應保障相關數據的收集，利用這些規則建立戰時海軍導彈器材供應保障決策知識庫，以期在未來海戰中提高導彈器材供應保障決策的科學性和時效性。