機動控位水雷協同定位系統可觀測性分析?

蔣 平 夏中亞 李加強

（1.西北工業大學航海學院 西安 710114）（2.中國船舶集團有限公司第七一0研究所 宜昌 443000）

1 引言

機動控位水雷在軍事領域有著廣闊的應用前景，是水雷通過組網、協同提升作戰效能，從單體作戰邁向集群作戰、體系作戰的重要載體。與傳統水雷相比，機動控位水雷需要同時具備導航控制、動力推進、質心調節、水聲通信等功能，要求具備“低能耗、高費效比”，因此機動控位水雷通常配備的是低精度的導航裝置。

以MEMS 的磁羅盤為核心的DR（航位推算）系統，結合GPS/北斗的衛星定位對DR 系統的累計誤差進行定位修正，是目前AUV 較為常用的低成本導航方法［1］，但是這種方法對機動控位水雷來說并不適用，一方面，隨著衛星、雷達和無人機/艇技術的發展，出水進行衛星定位修正會使得水雷武器的隱蔽性［2］經受嚴峻的考驗，另一方面，“上浮至出水定位修正-下潛調姿DR 導航”的工作模式，對系統功耗也提出了更苛刻的要求，因此，需要探索一種新的定位方法來滿足機動控位水雷的工作需求。

2 機動控位水雷水下協同定位

作為導航領域最值得研究的方向之一，協同定位一直以來都是熱點［3］，無論是在空中、地面、水下，還是軍用、民用等領域，都有著廣泛的應用前景。鑒于水中傳輸信道的衰減，以及水下環境的復雜性等客觀情況，水下協同定位技術的發展相對滯后。近年來，隨著聲學通信技術的發展，基于水聲通信的水下協同定位技術逐步成為發展重點［4～5］，這也為機動控位水雷水下定位提供了一種新的解決方案。

基于水聲通信的機動控位水雷水下協同定位方案［6］，是通過配備一艘或多艘具備高精度導航定位能力的水雷作為參照主節點，其余水雷作為從節點，僅配置低成本的DR系統，通過水聲通信機獲取主節點的精確位置信息，以及兩者之間的距離信息，通過移動長基線（MLBL）定位［7］原理進行自身定位誤差的協同校正，最終使導航性能得到顯著改善。

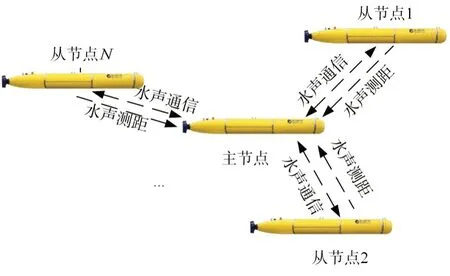
圖1 機動控位水雷協同導航結構圖（單領航節點）

3 運動模型

3.1 狀態方程

機動控位水雷采取航位推算的方式進行導航［8］，在水下的運動是三維的。水雷在Z 向的運動規矩實際上就是其所處的深度變化，可通過壓力變送器精確測量，因此可將三維的運動簡化為二維空間，對應的二維運動方程如下：

式（1）轉化為矩陣表達式，其中A（K）為狀態轉移矩陣：

3.2 觀測方程

從節點的機動控位水雷是通過主、從節點之間的距離信息進行定位誤差修正的，從節點位置信息（xk，yk，zk），接收到主節點的位置信息（），主、從節點的深度信息、zk可由壓力變送器測量獲得，主從節點的空間距離d3d,k可通過聲通機測量獲得，則在二維平面內主從節點距離dk計算公式為

因此距離信息的觀測方程為

建立線性化方程Hk：

其中，C（k）表示式（2）在（xk，yk）狀態下的的Jacobian矩陣，表示為

4 系統可觀測性分析

協同定位過程本質上是一種狀態預測，研究預測問題的首要前提就是系統必須是可觀測的［9］，只有確保系統可觀測，對應的測量值方能夠提供充足的信息進行狀態預測［10］。機動控位水雷協同定位系統是依靠聲學通信設備對參考節點單元進行相對距離觀測，設計前要針對距離觀測信息進行可觀測性分析，通過選取可觀測性強的工作狀態來提升協同定位的性能。

4.1 判定定理

對于如下形式的線性時變離散系統：

其中，x（k）為n 維狀態向量，y（k）為m 維輸出向量。系統在tk時刻完全可觀測的充要條件為在tk時刻后，存在某個時刻tN，使得N=[CCA…CAn-1]T滿秩，則系統是可觀測的。

4.2 可觀測性求解

機動控位水雷在水平面上的位置信息（xk，yk）是二維變量，式（2）觀測得到的距離信息是一維信息，因此至少要觀測兩次才能得到唯一解。基于兩次距離觀測的系統可觀測判別矩陣可表示為N(k,k+1)=[C(k)C(k+1)A(k+1)]T，計算得：

其中θk表示k 時刻相對距離觀測方位角，θk?[-π，π]。

由4.1 節定理可知，當且僅當系統可觀測矩陣滿秩時，系統是可觀測的，此時應滿足：sinθk≠sinθk+1且cosθk≠cosθk+1，即θk≠θk+1±π，僅當相鄰時刻測得的方位角是變化的，且變化值不等于π。

機動控位水雷進行協同定位時，為確保水聲通信可靠，一般處于低速直航狀態，典型的不可觀測的情況如圖2 所示：1）主節點和從節點沿著同一條直線航行；2）主節點和從節點沿著兩條并行線航行，且航行速度相同，相鄰兩次方位觀測角相同。

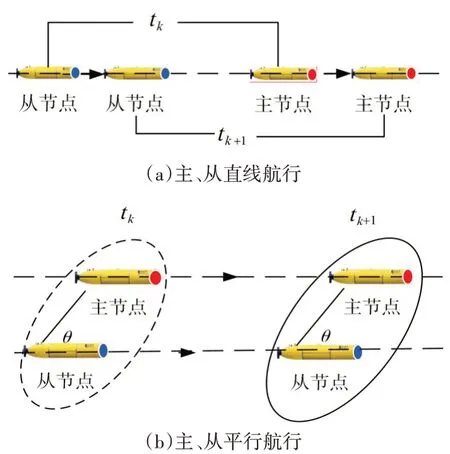
圖2 機動控位水雷處于不可觀測的典型情況

5 可觀測程度分析

上一節通過基于線性化模型的理論分析方法，得出了機動控位水雷在相鄰時刻測得的方位角是變化的，且變化值不等于π得情況下，系統是可觀測的，進而可通過距離觀測信息，實現可協同定位。在實際應用過程中，在明確系統可觀測性條件的基礎上，還要進一步分析系統的可觀測程度，即在不同條件下的系統可觀測程度強弱的問題，這樣才能確保在進行隊形控制時，盡可能地使系統處于易于觀測的狀態，從而確保協同定位的精度。

系統可觀測程度可通過觀測矩陣N 的二條件數cond2(N)來判斷，定義如下：

由于可觀測矩陣N是正規矩陣，因此：

其中λi為觀測矩陣的特征值，max |λi|、min |λi|分別表示最大和最小值。

條件數cond2(A)是大于1 的正數，根據條件數理論，若條件數越?。ń咏?），則系統的觀測性越好，反之若條件數越大，則觀測性越差，相同量測誤差情況下，定位精度越低［11］。

求解N的特征值過程如下：

解得特征值為

參考評文獻［12］中對式（3）的解析方法，得到可觀測矩陣N的可觀測度表達式為

其中Δθ=θk+1-θk，表示相鄰兩次主、從節點之間的觀測方位角的變化值，值域范圍［-π，π］。

系統可觀測度與觀測方位角變化值的對應關系見圖3 所示，由圖中可以看出，當方位角的變化值接近±π/2 時，可觀測度值趨近于1，表示此時可觀測程度為良態的，當方位角的變化值接近0（或者±π）時，可觀測度值趨近于∞，表示此時可觀測程度為病態的，在相同量測誤差下得到的估計誤差就較大。

圖3 系統可觀測度與觀測方位角對應關系

6 協同定位方案

根據第5 節可觀測程度的分析，通過測距方式來進行協同定位，要想取得良好的效果，觀測方位角要時刻保持較劇烈的變化，在進行協同定位系統方案設計時，為滿足良好的可觀測條件，可采取以下兩種配置方式：

1）在“一主多從”機制下，選取機動能力強的主節點，航行軌跡如圖4 所示，通過其直航過程中不斷調整速度，使得在相鄰時刻，觀測方位角保持一定的角度差；

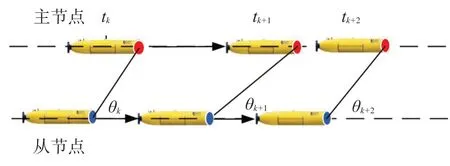
圖4 “一主多從”協同方案

2）配置兩個主節點，分別位于從節點的兩側，航行軌跡如圖5 所示，從節點依次對兩個主節點進行測距，tk效時刻以主節點1 為修正源，觀測方位角為θk，tk+1效時刻以主節點2 為修正源，觀測方位角為θk+1，tk+2效時刻又回到以主節點1 為修正源，觀測方位角為θk+2，依此類推。

圖5 “雙領航者”協同方案

對于機動控位水雷而言，頻繁地變速和調姿，不但會增加航路規劃的復雜度，還會對系統能耗造成較大影響，而且水雷的機動能力比較有限，一個通信周期內能產生的方位角差異較小，無法滿足良好的觀測度，因此方案1并不適用。

相比較而言，方案2 只需在初始時刻保持適當的隊形，每相鄰兩次得到的觀測方位角均位于不同的象限，航行過程中所有水雷均等速直航，即可等效實現并保持差異性，而且通過初始航路點的設置，容易實現相鄰兩次觀測角差值為±π/2，從而使系統一直處于理想的觀測狀態。方案2 缺點是增加了一個主節點，使得整個編隊系統成本有所增加。

7 結語

本文從機動控位水雷協同定位的需求入手，結合水雷自身的系統配置，通過聲學通信測距的方式來實現協同定位，并針對其可觀測性弱的問題，采用譜條件數理論進行了可觀測度量化分析，明確了系統可觀測度大小與協同定位節點運動狀態間的對應關系。在此基礎上，結合機動控位水雷自身的特點，設計了雙主節點的協同定位編隊方案。對水下協同定位而言，水聲通信的質量是決定性的，尤其在弱通信條件下，設計適用的非線性線性濾波算法，來實現協同定位系統的狀態估計，提升協同定位精度，是后續研究的重點。