三支概念背景下屬性粒化效率的度量*
張曉燕,王佳一
(西南大學人工智能學院,重慶 400715)
1 引言
形式概念分析[1]是一種以形式背景為研究對象的理論,是一種以概念格相關理論為核心概念的數學工具,常用于進行數據分析。概念格展示了概念之間的偏序關系,刻畫對象和屬性的內在關系[2]。然而,基本的概念格因其只研究了“共同(被)具有”關系的問題,忽略了“共同不(被)具有”關系的問題而存在局限性[3,4],且這種局限性也導致該理論在實際應用中受到限制[5]。
2014年,Qi[6]提出了新的理論以彌補經典概念格理論的局限性,即三支概念分析。三支概念分析提出了對象誘導的三支概念格與屬性誘導的三支概念格,2種三支概念格均同時研究了“共同(被)具有”和“共同不(被)具有”的問題。其所獲得的三支概念格相較于以往經典概念格研究范圍更加全面,也會使概念識別在實際應用過程中更加精確。
在三支概念正式提出后,許多學者對此進行了擴展和深入研究。Qian等[7]利用形式背景的疊置與并置,提出了三支概念格的構造方法,仿照對象誘導概念格與屬性誘導概念格提出了對象誘導的三支面向對象概念格和屬性誘導的三支面向屬性概念格的定義,并分析4種概念之間的異同。蘇新等[8]進行了基于對象和基于屬性的三支概念格合并方法比較。Wei等[9]立足于三支概念格,在三支協調的意義下研究了決策背景的規則獲取問題,并與強協調決策背景所獲得的一般決策規則進行了詳細的比較研究。
除對三支概念本身的擴展和推廣,學科交叉融合研究也為豐富三支概念體系做出了極大的貢獻。Li等[10]將多粒度與三支概念融合,提出了基于多粒度的三支認知概念學習。龍柄翰等[11]提出模糊三支概念分析,將模糊集理論與三支概念分析相結合,考慮模糊背景中“共同具有的程度”與“共同不具有的程度”2方面不確定的共性信息極大地提高了三支概念在生產力方面的意義。
多粒度研究方面,知識粒化[12]、屬性粒化[13,14]和屬性聚類[15]等概念的提出將多粒度與概念認知聯系起來[16],為了緩解龐大的概念個數,在約束寬松的情況下減少工作量提供了解決方案,并且為獲取數據的多層次概念知識表示與處理方法上提供了新的方法。多粒度方面的研究包括研究對象的粗化與細化,在屬性粒化研究中,其主要研究方向包括屬性的吸收,即粗化,以及屬性的分解,即細化。在屬性的粗化與細化之中,概念也會隨之轉化,可以獲得在不同粒度上的概念分析。Belohlavek等[17]提出了給予屬性粒化的形式概念分析方法,該理論中進行了屬性粒化,生成不同粒度層次的形式背景的工具主要是粒度樹與剪枝。
在三支概念格背景下,對屬性粒化的研究尚且不足,且現在無法通過有效手段度量屬性粒化效率,嚴重降低了概念區分與細化的速度,需要大量冗余的計算[18]。針對此種情況,本文提出以三支概念格為背景的屬性粒化效率度量方法,嘗試探討對解決此類問題的方法。
2 基礎知識
2.1 概念格
設有形式背景K=(G,M,I),其中,G為對象集,M為屬性集,I為G和M之間的二元關系。在經典形式背景中,I的取值只有0或者1這2種可能。對于x∈G,m∈M,當I(x,m)=1時,表示對象x和屬性m存在關系I;當I(x,m)=0時,表示對象x和屬性m不存在關系I。
為研究對象子集和屬性子集之間的關系,對于X?G,A?M,現定義如下2個分別作用于屬性子集和對象子集的導出算子X*和A*:
X*={m:m∈M,?x∈X,I(x,m)=1}
A*={x:x∈G,?m∈A,I(x,m)=1}
特別地,當對象子集或屬性子集中僅有一個元素時,記{x}*為x*,記{m}*為m*。
設有形式背景K=(G,M,I),若對于X?G,A?M,有X*=A且A*=X,則(X,A)稱為一個形式概念,其中概念的外延為X,概念的內涵為A。形式背景K=(G,M,I)下的所有形式概念的集合為L(K),L(K)即為概念格[20]。
本節內容詳見文獻[2]中有關于概念格的理論敘述。
2.2 三支概念格
如果說概念格研究的是“共同具有”的關系,那么三支概念格就是同時研究“共同具有”和“共同不具有”2種關系。在應用中,只研究單方面往往會使研究結果具有片面性,從而在利用概念尋找對象和屬性的過程中出現錯誤,而從正反2方面研究則會使研究結果更加精準,提高尋找結果的正確率。
為了研究“共同不具有”的關系,在這里定義2.1節導出算子的負算子。對于子集X?G,A?M,有:
顯然,在負算子作用下,“共同不具有”這一關系可以被研究。但是,如果需要同時研究具有和不具有的關系,還需要定義一對算子。特別需要說明的一點是,單個對象子集在運算后會得到2個屬性子集,即“共同具有的屬性”和“共同不具有的屬性”。同理,由于出發點不同,單個屬性子集在運算后會得到2個對象子集,從而可以得出2種概念。
對于X?G和A,B?M:
若XO=(A,B)且(A,B)O=X,則(X,(A,B))為對象誘導的三支概念,簡稱OE概念,其中,X為OE概念的外延,(A,B)為OE概念的內涵。
對于X,Y?G和A?M:
若AA=(X,Y)且(X,Y)A=A,則((X,Y),A)為屬性誘導的三支概念,簡稱AE概念,其中,(X,Y)為AE概念的外延,A為AE概念的內涵[21]。
本節內容詳見文獻[8]中有關三支概念格定義的敘述。
2.3 屬性粒化
屬性粒化是一種由舊的屬性集構建新的屬性集的方式,其構建方法是根據不同屬性的內在聯系,通過粒度樹與剪枝的構造得到不同的屬性集。相對于純代數構造方法,通過粒度樹這一工具的屬性粒化顯然要求屬性之間存在某種關聯,至少是人為規定的聯系。
對于形式背景K=(G,M,I),任意屬性m∈M,屬性m的粒度樹Tm是滿足以下全部條件的含有根節點的樹:
該樹中的任意一個節點都代表一個屬性,且都有確定且唯一的名稱來標記。樹的根節點為m。
對于每一個節點,此處記為z,均有一對象集合z*∈G,該對象集由具有屬性z的集合構成。
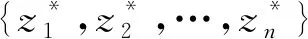
剪枝C是粒度樹Tm上滿足如下條件的節點集:對于每一個葉節點u而言,在從u到根節點m的路徑上存在唯一的節點存在于該剪枝。給定形式背景K=(G,M,I),如表1所示,其中,G={a,b,c,d,e}為對象集,M={Color, Black, Red, Blue, Light blue, Dark blue}為屬性集,I為G和M之間的二元關系。

Table 1 Formal background K=(G,M,I)
表1中基于屬性集的粒度樹如圖1所示。
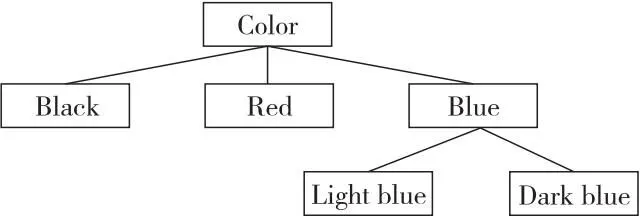
Figure 1 Granularity tree corresponding to attribute set in table 1
{Red,Light blue,Dark blue}不是剪枝,因為其到根節點Color的路徑上還有Black這一子節點。{Blue,Red,Light blue,Dark blue}是剪枝。

對于X?G,A?MC,有:
X*C={m:m∈MC,?x∈X,IC(x,m)=1}
A*C={x:x∈G,?m∈A,IC(x,m)=1}
得到粒度樹后,可以通過從粒度樹上獲取不同的剪枝得到不同的粒度層次,有些粒度層次之間存在偏序關系,而有些粒度層次之間不存在偏序關系。本文將對這2種情況分別進行討論。
本節內容詳見文獻[15]中關于粒度樹、剪枝及屬性粒化的敘述。
2.4 獲取概念格
引理1設K=(G,M,I)是一個形式背景,對于X,X0?G和A?M,下面性質成立:
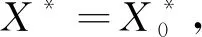
(2)若X*=A和X?A*,那么(A*,A)是一個概念。
引理1是Next Clousure算法的基礎,利用此概念可以獲得所有概念,所有的概念組成概念格L(K)。Next Clousure算法如算法1所示。

算法1 Next Clousure算法輸入:形式背景K=(G,M,I)。輸出:全部概念集合C。步驟1 初始化C=?;重命名全部對象為1:i;步驟2 令C=C∪{?**,?*};/*為對象子集和屬性子集導出算子,**是*的二次運算,即復合運算*/D=sort(G,DESC);/*將對象集元素進行分類并按降序排序*/步驟3 S=?*; while S≠?**do J=D-S; foreach i in Jdo F=(S∩{1,…,i-1}∪{i})*; T=F*; U=T∩{1,…,i-1}; if i∈T-S and S∩{1,…,i-1}=U then C=C∪{T,F}; S=T; break; endif endfor endwhile步驟4 return C
利用Next Clousure算法同樣可以得到反概念。反概念是相對概念而言的,反概念可以看作是原形式背景的補背景下的概念。對于一個形式背景,所有反概念組成該形式背景下的反概念格。
3 存在偏序關系的不同粒度層次
3.1 屬性粒化前后三支概念
屬性粒化前后,形式概念背景中的屬性集也隨之進行了粗細轉化,在由粗屬性集到細屬性集的轉化中,對于相同對象集,新屬性可能部分出現在與之對應的屬性集中,也有可能全部不出現在對應的屬性集中。
現實應用中,屬性粒化常用于更加精確地定義概念。例如,在將“不同種類牛仔褲”進行區分定義時,某屬性可以由“藍色”到“深藍色”及“淺藍色”,再到具體色號層層細化,使定義更加細化。而在屬性粒化由粗到細的過程中,隨著屬性集向更細的方向轉化,必定會有更多概念的形成。以下將對此結論進行理論證明。
為了方便說明,對于剪枝后的形式背景KC=(G,MC,IC)形成的概念格記為L(KC)。對于概念格中的概念數量,由于概念格本質上是集合,將其中元素的數目記為|L(KC)|。相似地,由這種概念格形成的面向對象三支概念格記為OEL(KC),面向屬性三支概念格記為AEL(KC)。
定理1在屬性粒化的過程中,隨著屬性粒度層次的細化,屬性集中元素的增多,概念格中概念的數量不會減少。
證明在屬性粒化過程中,對于任意屬性分解過程a→{a1,a2,…,al},若該屬性分解導致概念格中元素減少,則為在原概念格中存在概念的內涵B,a∈B的基礎上,新概念格中不存在概念的內涵BC,令BC∩{a1,a2,…,al}≠?。
對于新屬性集中的元素?ap(1≤p≤l)∈{a1,a2,…,al},設A=(M∩MC)∪{ap},則因為(A*C)*C=A*C*C,且(A*C*C)*C=A*C*C*C=A*C,因此(A*C,A*C*C)是一個概念格,因為A?A*C*C,所以ap∈A*C*C,則在新的概念格中存在概念內涵A*C*C∩{a1,a2,…,al}≠?。以上假設不成立,即任意屬性分解均不會造成概念格中元素減少,原定理得證。
類似地,有如下定理:
定理2在屬性粒化的過程中,隨著屬性粒度層次的細化,屬性集中元素增多,面向對象三支概念格中概念的數量不會減少。
定理3在屬性粒化的過程中,隨著屬性粒度層次的細化,屬性集中元素的增多,面向屬性三支概念格中概念的數量不會減少。
3.2 細化系數
為了研究屬性聚類對三支概念的影響,需要在同一對象集下,進一步建立屬性聚類前后三支概念的聯系。對于屬性集M={m1,m2,…,m|M|},聚類后表示為MR={([m]R)1,([m]R)2,…,([m]R)k}(k≤|M|),其中,R為聚類關系,?1≤p,q≤k,且p≠q,根據等價類與集合的性質,([m]R)p∩([m]R)q=?。定義一般屬性聚類中的算子與負算子,對于X?G和A?MR:如果在定義事物的時候,選擇描述事物的關鍵詞越多,分類越細致,對于事物的定義就會越精確。相似地,概念格在不同的屬性層次移動,由粗到細的時候,概念也會由粗到細,得到更加精確的概念。概念格中概念的數量也會隨之變化。根據定理1,較粗屬性層次對應的概念格中的概念數量會大于或等于較細屬性層次對應的概念格中概念的數量,因此可以通過比較層次移動時概念格中概念數量的變化來比較屬性粒化的效果。
定義1對于屬性粒化層次C1和C2,若存在偏序關系C1≤C2,即前者是后者的細化,在度量細化時,定義細化系數eLC如式(1)所示:
(1)
細化系數eLC越大,表明新的屬性層次產生了越多的新概念,此次屬性粒化越有效。
相似地,根據定理2和定理3,可以定義出與以上細化系數相同的面向對象細化系數和面向屬性細化系數。
定義2對于屬性粒化層次C1和C2,若存在偏序關系C1≤C2,即前者是后者的細化,在度量細化時,定義面向對象細化系數eOELC如式(2)所示:
(2)
定義3對于屬性粒化層次C1和C2,若存在偏序關系C1≤C2,即前者是后者的細化,在度量細化時,定義面向屬性細化系數eAELC如式(3)所示:
(3)
以下用示例說明2種細化系數的用法。
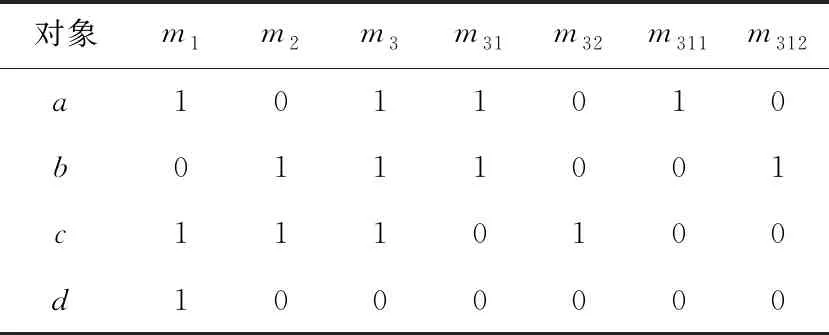
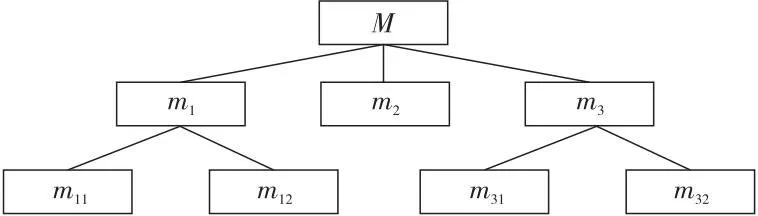
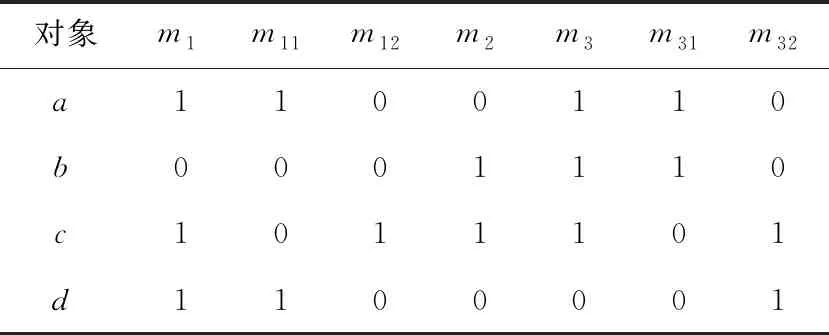
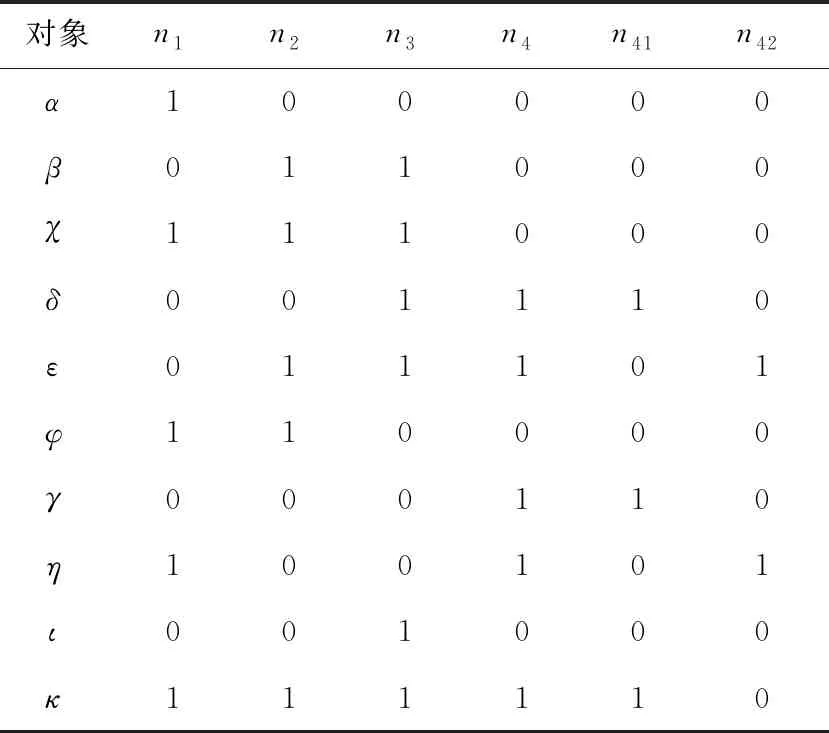
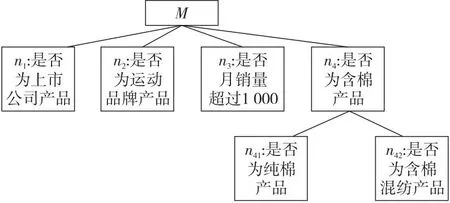
例1現有一購物網站搜索場景利用如表2所示形式背景K=(G,M,I)表示,其中,M={m1,m2,m3},MC1={m1,m2,m31,m32},MC2={m1,m2,m31,m321,m322}。對象代表4種不同的鞋品,屬性代表商品的特征,m1,m2和m3分別代表網面材質、黑色和安踏品牌,且粒度樹如圖2所示。對于存在偏序關系C2 Figure 2 Granularity tree of table 2 Table 2 Formal background K=(G,M,I) for example 1 計算可得: |OEL(K)|=8,|AEL(K)|=7,|OEL(KC1)|=11,eOELC1=11/8,|AEL(KC1)|=10,eAELC1=10/7。 同理,|OEL(KC2)|=12,eOELC2=12/11>1;|AEL(KC2)|=15,eOELC2=3/2>1。該屬性粒化在C2上存在意義。 在實際應用中,經常使用屬性粒化對現有概念進行細化,而屬性細化方向的選擇則與屬性粒化的效率息息相關,細化方向選擇的不同會導致屬性粒化效率的差別,例如,在試圖細化“牛仔褲”這個概念的時候,存在多種細化方向,顯然,將“藍色”細化為“深藍色”和“淺藍色”相較于將“紅色”細化為“淺紅色”和“深紅色”更加有效。 例2現有一購物網站搜索場景利用如表3所示的形式背景K=(G,M,I)表示,其中,M={m1,m2,m3},MC1={m1,m2,m31,m32},MC3={m11,m12,m2,m3}。對象代表4種不同的鞋品,屬性代表商品的特征,m1,m2和m3分別代表網面材質、黑色和安踏品牌,且粒度樹如圖3所示。不存在偏序關系的屬性粒化層次及生成的新形式背景KC1=(G,MC1,IC1)和KC3=(G,MC3,IC3),m11和m12分別代表全網面鞋和半網面鞋,m31和m32分別代表安踏品牌休閑系列與安踏品牌運動系列。 Figure 3 Granularity tree of table 3 Table 3 Formal background K=(G,M,I) for example 2 Table 4 Formal background K=(G,M,I) for example 3 計算可得: |OEL(KC3)|=10,eOELC3=5/4 |AEL(KC3)|=10,eAELC3=10/7=eAELC1 因此,屬性粒化方向C1優于C3。 在具體的現實操作中,細化方向的選擇往往更加復雜,且相較于以上實例更加抽象和不直觀,因此通過細化算子來度量不存在偏序關系的不同粒度層次的優劣,以此來選擇粒度層次進行進一步細化,從而避免冗余的計算和資源的浪費,是十分有必要的。 以下一組定理是獲取面向對象三支概念格與面向屬性三支概念格的理論依據。 定理4設K=(G,M,I)是一個形式背景,若(X,A)是一個概念且(X,B)是一個反概念,那么(X,(A,B))一定是一個OE概念,記由此得到的概念集合為O1。 定理5設K=(G,M,I)是一個形式背景,若(X,A)是一個概念且(Y,B)是一個反概念,且Y為X的最小上界,X不屬于FL(K)的外延集,那么(X,(A,B))一定是一個OE概念,記由此得到的概念集合為O2。 定理6設K=(G,M,I)是一個形式背景,若(X,A)是一個概念且(Y,B)是一個反概念,且X為Y的最小上界,Y不屬于L(K)的內涵集,那么(Y,(A,B))一定是一個OE概念,記由此得到的概念集合為O3。 定理7設K=(G,M,I)是一個形式背景,若(X,A)是一個概念且(Y,B)是一個反概念,且X,Y均為X∩Y的最小上界,X不屬于FL(K)的外延集,Y不屬于L(K)的內涵集,那么(X∩Y,(A,B))一定是一個OE概念,記由此得到的概念集合為O4。 定理8設K=(G,M,I)是一個形式背景,則OEOL(K)=O1∪O2∪O3∪O4。 定理9設K=(G,M,I)是一個形式背景,若(X,A)是一個概念且(Y,A)是一個反概念,那么((X,Y),A)一定是一個AE概念,記由此得到的概念集合為A1。 定理10設K=(G,M,I)是一個形式背景,若(X,A)是一個概念且(Y,B)是一個反概念,且B為A的最小上界,A不屬于FL(K)的內涵集,那么((X,Y),A)一定是一個AE概念,記由此得到的概念集合為A2。 定理11設K=(G,M,I)是一個形式背景,若(X,A)是一個概念且(Y,B)是一個反概念,且A為B的最小上界,B不屬于L(K)的內涵集,那么((X,Y),B)一定是一個AE概念,記由此得到的概念集合為A3。 定理12設K=(G,M,I)是一個形式背景,若(X,A)是一個概念且(Y,B)是一個反概念,且A,B均為A∩B的最小上界,A不屬于FL(K)的內涵集,B不屬于L(K)的內涵集,那么((X,Y),A∩B)一定是一個AE概念,記由此得到的概念集合為A4。 定理13設K=(G,M,I)是一個形式背景,則AEPL(K)=A1∪A2∪A3∪A4。 根據以上理論可以獲取eOELC,如算法2所示。 算法2 獲取eOELC輸入:概念格L(K),L(KC)與反概念格FL(K),FL(KC)。輸出:參數eOELC。步驟1 初始化O1=?,O2=?,o1=0,o2=0;步驟2 令LpG∩FqG=W;if W=LpG且W=FqG then O1=O1∪(W,(LpM,FqM)); /*LpG和LpM分別表示在L(K)中概念的外延和內涵,FqG和FqM分別表示在FL(K)中反概念的外延和內涵*/else if W=LpG,W≠FqG且FqG為W最小上界 then O1=O1∪(W,(LpM,FqM)); else if W≠LpG,W=FqG且LpG為W最小上界 then W1=W1∪(W,(LpM,FqM));else if W≠LpG,W≠FqG且LpG與FqG均為W最小上界 then O1=O1∪(W,(LpM,FqM));end ifo1為O1中元素的個數;步驟3 令LpGC∩FqGC=V;if V=LpGC且V=FqGC then O2=O2∪(V,(LpMC,FqMC)); /*LpGC和LpMC分別表示在L(KC)中概念的外延和內涵,FqGC和FqMC分別表示在FL(KC)中反概念的外延和內涵*/else if V=LpGC,V≠FqGC且FqGC為V最小上界 then O2=O2∪(V,(LpMC,FqMC));else if V≠LpGC,V=FqGC且LpGC為V最小上界 then O2=O2∪(V,(LpMC,FqMC));else if V≠LpGC,V≠FqGC且LpGC與FqGC均為V最小上界 then O2=O2∪(V,(LpMC,FqMC));end if步驟4 eOELC=o2/o1;步驟5 輸出eOELC 例3現某購物網站需要對搜索機制改良,對10件短袖的標簽進行細分,根據最新網絡關鍵詞捕捉報告,近期“全棉”與“含棉混合面料”的區別引起消費者廣泛討論,故生成如圖4所表示的粒度樹。 Figure 4 Granularity tree of commodity research 根據粒度樹與“商品-標簽”對應關系,有如表4所示形式背景K=(G,M,I)和KC=(G,MC,I),其中,G={α,β,…,τ},M={n1,n2,n3,n4},MC={n1,n2,n3,n41,n42}。 現以此例,從準確性和效率性評估算法2(與直接計算作比較)。 利用直接計算方法,求得OEL(K)需要進行算子計算(包括正算子和負算子)544次,交集運算256次,比較運算512次,最后得出|OEL(K)|=33;求得OEL(KC)需要進行算子計算(包括正算子和負算子)2 112次,交集運算1 024次,比較運算2 048次,最后得出|OEL(KC)|=52。共計使用算子計算2 656次,交集運算1 280次,比較運算2 560次。最終計算得出eOELC=52/33。 利用本文的改進算法Next Clousure算法計算概念格與反概念格。計算K的概念格使用算子運算32次,比較運算16次;計算KC的概念格使用算子運算64次,比較運算32次。利用2個計算結果進一步計算eOELC的過程中,使用交集運算1 280次,比較運算256次,最終輸出eOELC=52/33。 在實驗過程中,需要尤為注意的是,算子計算的復雜度與其他計算是不可同日而語的。以本數據集為例,一次算子計算包含4~50次的運算;而一次比較計算至多只涉及5次對應計算。因此,效率性的評估以算子計算的數目為主要評價指標。 綜上,在計算eOELC時,使用本文提出的算法相較直接計算方法大幅減少了正算子及負算子的計算量,極大降低了計算復雜度。2次計算輸出的eOELC相等。算法2相比直接計算方法在保證準確性的前提下,極大提升了計算效率。 根據以上理論可以獲取eAELC,如算法3所示。 算法3 獲取eAELC輸入:概念格L(K),L(KC),與反概念格FL(K),FL(KC)。輸出:參數eAELC。步驟1 初始化A1=?,A2=?,a1=0,a2=0;步驟2 令LpM∩FqM=N;if N=LpM且N=FqM then A1=A1∪((LpG,FqG),N); /*LpG和LpM分別表示在L(K)中概念的外延和內涵,FqG和FqM分別表示在FL(K)中反概念的外延和內涵*/else if N=LpM,N≠FqM且FqM為N最小上界 then A1=A1∪((LpG,FqG),N);else if N≠LpM,N=FqM且LpM為N最小上界 then A1=A1∪((LpG,FqG),N);else if N≠LpM,N≠FqM且LpM,FqM均為N最小上界 then A1=A1∪((LpG,FqG),N);end ifa1為A1中元素的個數;步驟3 令LpMC∩FqMC=Q;if Q=LpMC且Q=FqMC then A2=A2∪((LpGC,FqGC),Q);else if Q=LpMC,Q≠FqMC且FqMC為Q最小上界 then A2=A2∪((LpGC,FqGC),Q);else if Q≠LpMC,Q=FqMC 且LqMC為Q最小上界 then A2=A2∪((LpGC,FqGC),Q);else if Q≠LpMC,Q≠FqMC且LpMC,FqMC均為Q最小上界 then A2=A2∪((LpGC,FqGC),Q);end ifa2為A2中元素的個數;步驟4 eAELC=a2/a1;步驟5 輸出eAELC 接例3,從準確性和效率性評估算法3(與直接計算作比較)。 利用直接計算方法,求得AEL(K)需要進行算子計算64次,交集運算16次,比較運算32次,最后得出|AEL(K)|=12;求得AEL(KC)需要進行算子計算(包括正算子和負算子)128次,交集運算32次,比較運算64次,最后得出|AEL(KC)|=17。共計使用算子計算192次,交集運算48次,比較運算96次。最終計算得出eAELC=17/12。 利用本文改進算法Next Clousure算法計算概念格與反概念格。計算K的概念格使用算子運算32次,比較運算16次;計算KC的概念格使用算子運算64次,比較運算32次。利用2個計算結果進一步計算eAELC過程中,使用交集運算1 280次,比較運算256次,最終輸出eAELC=17/12。2次計算輸出的eAELC相等。 綜上,在計算eAELC時,使用本文提出算法相比直接計算方法減少了正算子及負算子的計算量。算法3相比直接計算方法在保證準確性的前提下,極大地提升了計算效率。 本文對概念格、三支概念格以及屬性粒化的定義及性質進行了概述,并且研究了屬性粒化前后三支概念的關系,定義細化系數,以此度量屬性粒化的效率。本文研究結果仍存在不能精確選擇、不能進行精確性度量等問題。下一步將針對目前發現的問題進行深入的研究。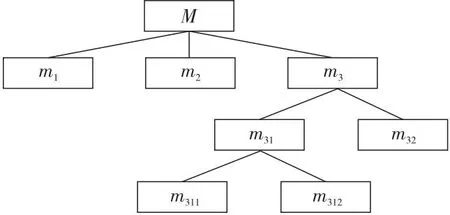
4 不存在偏序關系的不同粒度層次
5 算法
5.1 理論依據
5.2 獲取eOELC算法

5.3 獲取eAELC算法

6 結束語

