基于拉丁超立方體的改進白骨頂雞算法

何星月，張 靖，覃 濤，何必濤，楊 靖+

(1.貴州大學 電氣工程學院，貴州 貴陽 550025；2.中國電建集團 貴州工程有限公司，貴州 貴陽 550025)

0 引 言

元啟發式算法是對自然界的生物現象或物理現象進行模擬，可以在高維且復雜的約束條件下快速地找到問題的全局最優解。近年來一系列的元啟發式算法被提出[1-4]，這些算法被廣泛的應用于圖像分割、參數估計、特征選擇等領域[5-9]。

白骨頂雞算法由Iraj Naruei等[10]提出。通過對白骨頂雞的隨機運動、鏈式運動和領導運動等行為的模擬，構建出一種有效的尋優機制。相較于傳統算法，白骨頂雞算法具有結構簡單、性能穩定等優點，但仍存在收斂速度慢、易陷入局部最優等不足。

為改善上述缺陷，國內外學者們提出了不同的改進策略。文獻[11]提出了一種刺激-響應機制，根據響應閾值，使蜜蜂在跟隨蜂和雇傭蜂之間轉換，以平衡算法的搜索與開發能力。文獻[12]根據三角形相似性原理提出了動態演化理論，以增強麻雀算法后期的開發能力。文獻[13]利用差分進化思想，在樽海鞘領導者位置更新中引入變異算子，幫助算法在后期跳出局部最優。文獻[14]通過對正余弦算法搜索方程中引入社交和認知成分，結合灰狼算法良好勘探和開發平衡能力優化了算法的尋優性能。

為進一步提高算法尋優精度及工程應用價值，本文提出了基于拉丁超立方體的改進白骨頂雞算法(improved COOT algorithm based on Latin Hypercube，LHCOOT)。首先利用拉丁超立方體抽樣使種群分布更加均勻；引入非線性決策因子以權衡算法全局搜索和局部開發過程；采取動態邊界機制，加速算法收斂；對最優個體進行柯西擾動并引入貪婪策略，避免算法陷入局部最優。通過對16個基準函數、高維函數和實際工程問題進行仿真實驗，驗證了LHCOOT算法的有效性。

1 白骨頂雞算法COOT

白骨頂雞是一種小型水鳥，在水面上有許多不同的群體行為，包括普通個體的隨機運動、鏈式運動、引導運動以及領導者運動。該算法的具體步驟如下：

普通個體運動：該過程主要由3種運動狀態構成，執行機制如式(1)所示

(1)

式中：Rb、Rc為常量0.5。lead、chain、random表示引導運動、鏈式運動和隨機運動，分別如式(2)～式(4)所示

CootPos(i)=Lead(K)+2×R1×cos(2R)×
(Lead(K)-CootPos(i))

(2)

(3)

CootPos(i)=CootPos(i)+A×R2×(Q-CootPos(i))

(4)

式中：R是[-1，1]中的隨機數，R1、R2是[0，1]中的隨機數，K為領導者的索引，為普通個體分配領導者，如式(5)所示

K=1+(iMODNL)

(5)

式中：i是普通個體索引，NL為領導者的數量。

領導者運動：該運動根據式(6)，利用最優個體牽引領導者，幫助種群向最優區域收斂

(6)

式中：gBest是當前最優個體位置，R3和R4是[0，1]中的隨機數。

2 改進白骨頂雞算法LHCOOT

2.1 基于拉丁超立方體的初始化種群

元啟發式算法的收斂速度和收斂精度通常與初始種群的分布結構息息相關。COOT算法以隨機方式生成的初始種群會導致個體在求解空間分布不均，影響初始種群的多樣性。相較于傳統的混沌映射[15]、佳點集[16]等初始化策略，拉丁超立方體抽樣[17](Latin Hypercube sampling，LHS)基于分層抽樣原理，可以實現非重疊采樣和變量范圍全覆蓋采樣，兼顧種群初始化的隨機性和均勻性。

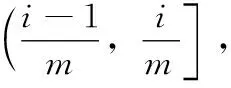
(7)

式中：vij是與hij獨立的(0，1)上均勻分布的獨立蒙特卡洛樣本。按照上述步驟選取的m個點ci=(ci1，ci2，…，cim)，i=1，2…m為一個拉丁超立方體樣本。

假設搜索空間為2維，搜索范圍為(0，1)。隨機種群初始化和拉丁超立方體初始化分布如圖1所示。

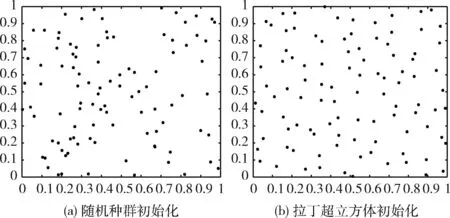
圖1 初始化種群分布

從圖1可以觀察到，隨機種群初始化個體粘連嚴重，均勻性不佳。拉丁超立方體初始化分布在整個解空間，且均勻分散在每個坐標區間。因此，拉丁超立方體抽樣能有效提高初始種群多樣性，有助于加快算法收斂速度。

2.2 混合位置更新策略

2.2.1 非線性決策因子

是否能合理地平衡算法全局搜索和局部開發能力將直接影響算法的尋優能力。在COOT算法中，隨機運動將會在解空間生成一個隨機解，引導白骨頂雞位置更新。鏈式運動將兩個相鄰索引個體的平均位置作為更新位置。因此，鏈式運動幫助種群向同一方向匯聚，適合在算法前期加速算法收斂。而隨機運動在整個解空間生成一個隨機解，牽引算法跳出局部最優。兩種位置更新的執行機制如式(8)所示

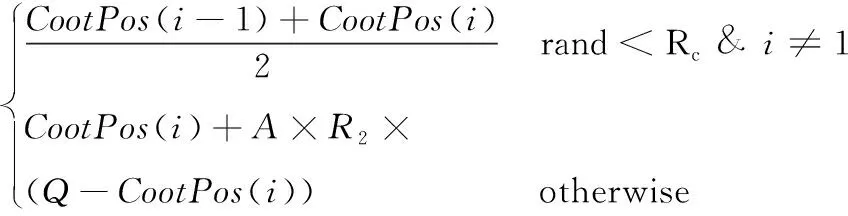
(8)

因此，等于0.5的常量Rc，是控制算法全局搜索能力和局部開發能力的決策因子。常量型決策因子并不能適用于解決復雜高維的實際工程問題。因此，本文采用一種非線性決策因子，令算法在前期緩慢衰減，增大執行鏈式運動的概率，幫助算法快速收斂。在算法后期迅速衰減，增大執行隨機運動的概率，從而幫助算法跳出局部最優。非線性決策因子的數學模型如式(9)所示

(9)

式中：Rv0為決策因子初值，本文取為1，t是模型控制因子，t的取值控制模型的衰減速度，t值越大，模型的衰減速度越慢。不同t值下非線性決策因子模型及常量0.5對比如圖2所示。

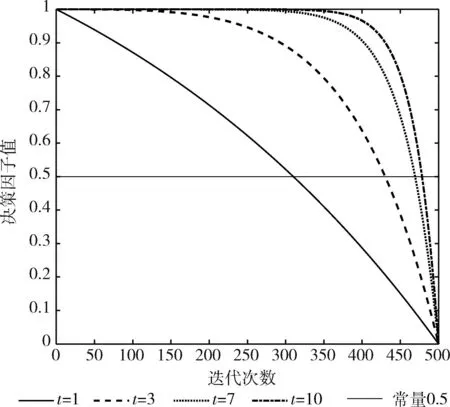
圖2 決策因子曲線

當決策因子曲線在常量0.5上方時，算法會以大概率執行鏈式運動。反之，會以大概率執行隨機運動。經多次實驗驗證，當t取10時，算法效果最佳。

2.2.2 自適應動態邊界

COOT算法在執行隨機運動時，會在整個搜索空間中生成隨機解。如果該搜索空間不隨著迭代過程而相應收斂，將會增大尋優過程的盲目性和復雜度，造成算法收斂遲滯，迭代時間增加。因此，本文引入了自適應動態邊界機制，加快算法收斂速度。動態邊界的上下界如式(10)所示

UB=α×max(X)
LB=α×min(X)

(10)

式中：X為整個種群的位置矩陣，α為自適應映射系數，如式(11)所示

α=1+0.2×(eL/Iter-1)

(11)

式中：L是當前迭代次數，Iter是最大迭代次數。隨機位置Q的生成如式(12)所示

Q=rand(1，d)×(UB-LB)+LB

(12)

從式(12)可以看出，邊界將隨著種群的移動而動態跟隨，隨著種群的收斂而相應縮小。同時，為了避免迭代后期，種群收斂陷入局部最優，將動態邊界通過隨著迭代次數增大的映射系數放大，增加動態牽引力度，從而增大跳出局部最優的概率。相較于逐維更新的動態邊界，利用種群確定邊界，可以避免不同維度間的相互干擾，提供一定裕量，提高尋優能力。

2.3 柯西變異

領導者的迭代更新由最優個體引導，向著最優位置靠近，導致算法后期種群多樣性降低，算法易陷入局部最優。本文在原有算法中加入柯西變異算子，對最優個體進行柯西擾動，擴大算法的局部搜索能力，增強種群的多樣性。

正態分布和柯西分布是兩種經典的連續型概率分布，兩者的概率密度函數曲線如圖3所示，相較于正態分布，柯西分布原點處的峰值較小，從原點處的峰值到兩端的下降趨勢會更加平緩。因此，柯西變異擾動能力更強。通過融入柯西變異對最優個體產生擾動，能夠幫助算法跳出局部極值。

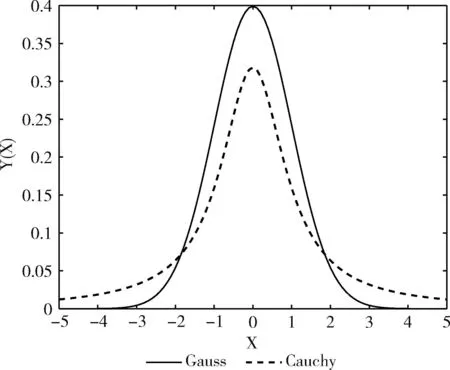
圖3 概率密度函數曲線

對最優個體添加柯西變異的模型為

Xnbest=Xbest×(1+cauchy(0，1))

(13)

式中：Xbest為最優個體，Xnbest為變異后的個體，cauchy(0，1) 是服從中心為0，尺度參數為1的柯西分布隨機數。為保證變異之后的解優于原始解，算法引入貪婪策略，對比擾動前后解的適應度值，擇優保留。貪婪策略的數學模型如式(14)所示

(14)

式中：f為適應度函數。

2.4 改進算法流程圖

綜合上述改進策略，LHCOOT的算法流程如圖4所示。

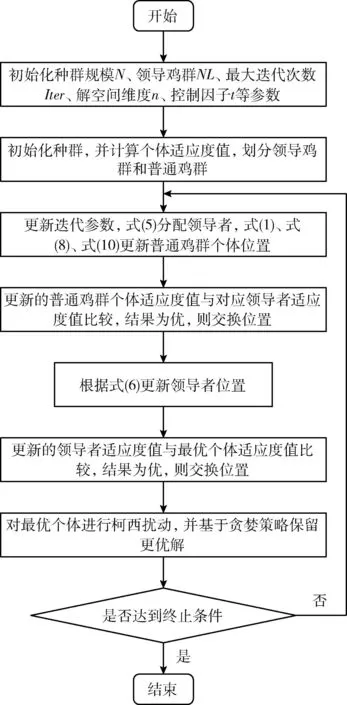
圖4 算法流程

2.5 時間復雜度分析

時間復雜度作為評價算法性能的指標之一，可以間接反映算法的尋優效率。設標準白骨頂雞算法種群數量為N，搜索空間維度為n，最大迭代次數為M，領導雞群比例為NL，求解目標函數適應度時間為f(n)。 假設初始化參數時間為λ1，每一維產生服從均勻分布隨機數的時間為λ2，找到并保存適應度最佳個體位置的時間為λ3，則算法總體初始化階段的時間復雜度為

T1(n)=O(λ1+N(nλ2+f(n))+λ3)=O(n+f(n))

在迭代過程中，普通個體更新階段，普通個體個數為N(1-NL)， 設隨機運動、鏈式運動、領導運動每一維更新位置時間都近似為λ4，式(7)的決策機制時間為λ5，計算位置更新后的適應度并與最優位置比較的時間為λ6，根據式(3)更新參數A的時間為λ7，則此階段時間復雜度為

T2(n)=O(N(1-NL)(nλ4+f(n)+λ5+λ6)+λ7)=
O(n+f(n))

在領導者更新階段，領導者個數為N×NL，設白骨頂雞領導者每一維位置更新所需的時間為λ8，計算位置更新后的適應度并與最優位置比較的時間也為λ6，根據式(9)更新參數B的時間為λ9，則這一階段的時間復雜度為

T3(n)=O((N×NL)(nλ8+f(n)+λ6)+λ9)=
O(n+f(n))

由此，COOT算法總時間復雜度為

T(n)=T1(n)+M(T2(n)+T3(n))=O(n+f(n))

在LHCOOT中，在初始化階段，引入了拉丁超立方體抽樣初始化種群，相較于均勻分布初始化種群，算法時間復雜度保持不變，即T′1=T1； 在普通個體更新階段，設引入非線性決策因子時間為t1，貪婪策略的時間為t2，自適應動態邊界包含在隨機運動更新位置時間仍然為λ4，因此LHCOOT算法這一階段的復雜度為

T′2(n)=O(N(1-NL)(n(λ4+t1)+f(n)+
λ5+λ6+t2)+λ7)=O(n+f(n))

在領導者更新階段，設柯西擾動的時間為t3，貪婪策略的時間仍為t2，則該階段時間復雜度為

T′3(n)=O((N×NL)(nλ8+f(n)+λ6)+λ9+
t2+t3)=O(n+f(n))

因此，LHCOOT算法總時間復雜度為

T′(n)=T′1(n)+M(T′2(n)+T′3(n))=O(n+f(n))

綜上所述，與COOT算法相比，LHCOOT算法所引入的改進策略并不會增加算法時間復雜度。

3 實驗結果及分析

3.1 對比算法及參數設置

本文采用的仿真軟件為MATLAB 2015b，實驗環境為i7-10750H CPU，2.69 GHz主頻，16 GB運行內存，操作系統為Windows 10(64位)。

選取粒子群算法(particle swarm optimization，PSO)、金豺優化算法(golden jackal optimization，GJO)、樽海鞘群算法(salp swarm slgorithm，SSA)、白骨頂雞算法(COOT)、添加非線性決策因子的白骨頂雞算法(NDFCOOT)、融合Tent映射和萊維飛行的改進白骨頂雞算法[18](COOTTLCR)與本文LHCOOT算法進行對比實驗，上述算法統一最大迭代次數為500，種群規模為30，為降低算法結果偶然性，皆獨立運行30次。各算法參數設置見表1。

表1 對比算法參數設置

3.2 測試函數

為了檢驗LHCOOT算法的尋優能力，本文選取文獻[18]中的16個基準測試函數進行仿真驗證，分別是單峰測試函數中的f1～f7，多峰測試函數中的f8～f13，固定維測試函數中具有代表性的f20、f22、f23，其中單峰與多峰測試函數維度為30。

3.3 尋優精度分析

表2中的平均值和標準差分別反映出算法的尋優能力和穩定性。對于單峰測試函數，LHCOOT算法在f1～f4函數上遠優于其它算法，能夠100%尋到函數的理論最優值。在測試函數f6上LHCOOT算法僅僅以微弱的差距次于SSA算法。在f5與f7測試函數上，LHCOOT算法也都優于其余元啟發式算法。LHCOOT算法對單峰函數良好的尋優效果體現了其有著出色的全局搜索能力。

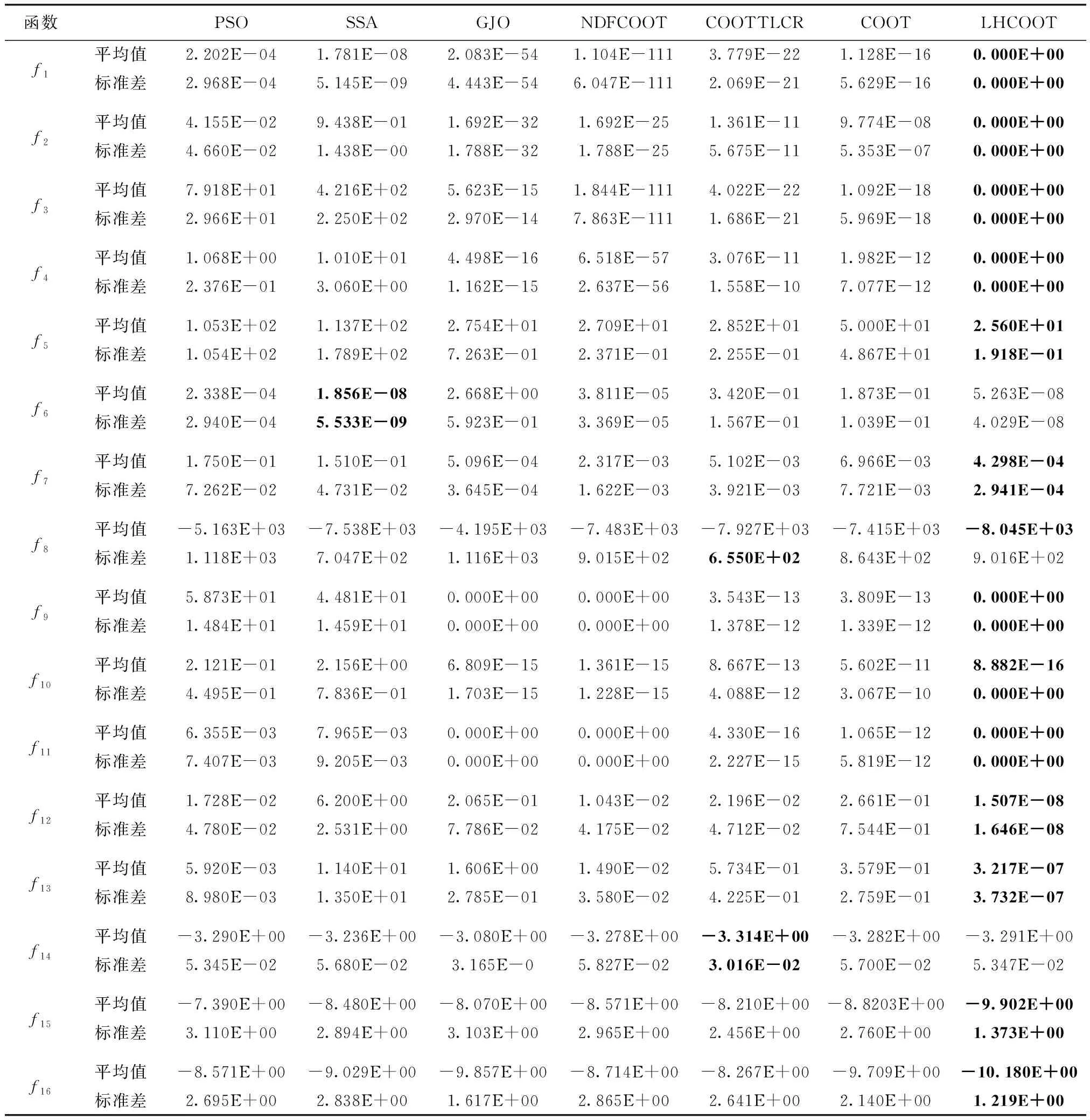
表2 基準測試函數尋優結果對比

對于多峰測試函數，LHCOOT算法在尋優精度上均優于其它算法。其中，在函數f9、f11上，LHCOOT算法達到了100%的尋優率。在函數f12、f13上，LHCOOT算法的尋優精度遠遠高于其它元啟發式算法，超過了2～3倍數量級的尋優精度。在函數f8上，LHCOOT算法雖然標準差稍次于COOTTLCR算法，但尋優精度仍然保持最優。對于固定維度測試函數，在函數f14上，LHCOOT算法僅次于COOTTLCR算法，且已較接近理論最優值。在函數f15、f16上，LHCOOT算法也保持著最好的尋優精度。

相較于COOT算法，NDFCOOT算法與LHCOOT算法在f1～f4以及f6函數上都取得了明顯得進步，說明引入非線性決策因子，可以提高算法的全局搜索能力，加快算法收斂。而在多峰函數上NDFCOOT算法表現不佳，說明單一的非線性決策因子策略對后期跳出局部最優幫助較低。而添加了柯西變異的LHCOOT算法，可以有效解決多峰函數上陷入局部極值點的問題。

綜上，LHCOOT算法在選取的測試函數上的表現優于其它6種算法，驗證了算法良好的搜索能力和尋優精度。

3.4 算法收斂曲線

為了更清晰刻畫算法的動態尋優性能，圖5給出了PSO、SSA、GJO、NDFCOOT、COOTTLCR、COOT、LHCOOT這7種算法在上述基準測試函數(部分)的收斂曲線。從選擇出的9個測試函數的收斂曲線上，可以看出LHCOOT算法比標準的COOT算法以及其余各個算法收斂速度更快，收斂精度更高。

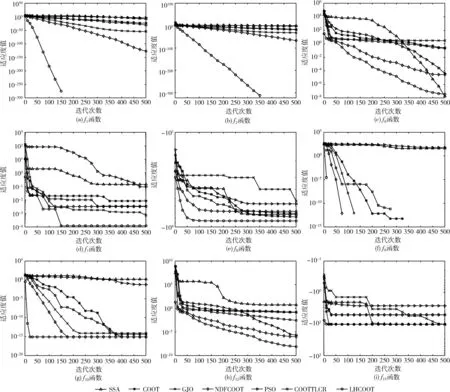
圖5 對比算法收斂曲線

其中，函數f1和f2尋優效果遠遠好于其它算法，分別迭代了150次和340次便成功找到理論最優值。這歸功于拉丁超立方體抽樣的非重疊采樣和全覆蓋采樣，使得初始種群多樣性遠高于其它算法的隨機初始化種群，有效加速算法收斂速度和收斂精度。在函數f7、f8、f9和f10上，雖然LHCOOT算法尋優精度優勢微弱，但收斂速度均為第一，收斂曲線在迭代前期便能迅速下降。在函數f6上，雖然收斂精度略次于SSA算法，但收斂速度在前期遠遠超過SSA算法。這表明自適應動態邊界機制，生成的邊界空間可以動態跟隨種群的變化，大大加快算法收斂速度。同時依賴于非線性決策因子有效平衡了算法全局搜索和局部開發過程，增強了算法的尋優能力。

在多峰測試函數f12上，LHCOOT算法在500次迭代結束時仍然保持著收斂狀態，尋優精度仍會隨著迭代次數增加而增加。相較于GJO算法和COOT算法等過早陷入局部最優，收斂精度提升緩慢甚至停滯，LHCOOT算法由于對最優解使用了柯西擾動策略，逃離局部最優能力顯著增加。

通過綜合對比分析，相較于其它6種元啟發式算法，LHCOOT算法的收斂速度和收斂精度占優，且有著較好逃離局部最優能力。

3.5 不同維度下算法對比分析

為了檢驗算法在高維度、大規模問題下的尋優能力，選擇LHCOOT算法與PSO、SSA、GJO、COOT算法對比。對表1中的單峰函數f1～f4和多峰函數f11～f13這7個基準測試函數在維度D=50/100/300時進行尋優。得出的實驗結果見表3。

表3 不同維度對比結果

從實驗結果可以看出，在各種高維情況下的單峰測試函數和多峰測試函數，LHCOOT算法的尋優精度均高于PSO、SSA、GJO、COOT算法。

對于單峰測試函數，LHCOOT算法在50/100/300維中，都能夠收斂到理論最優值，且標準差皆為0，體現了算法良好的魯棒性和尋優能力。而其它4種算法在一定程度上收斂精度會隨著維度的增加而降低。由此可見，LHCOOT算法在求解單峰問題上未陷入“維數災難”。

對于多峰測試函數，在函數f11上，LHCOOT算法取得了不錯的收斂精度，且收斂精度與30維條件下一致，可見算法對高維度、大規模問題具有不錯的魯棒性。在函數f12、f13上，雖然LHCOOT算法的收斂精度和標準差未達到理想值，但收斂精度仍然高出其余各算法1～5個數量級不等。體現了LHCOOT算法具有良好的全局搜索和局部開發能力。

綜上所述，LHCOOT算法在解決高維度、大規模問題時，對維度的變化不敏感，仍然保證了良好的尋優精度。其算法魯棒性、尋優能力均優于其余4種算法。

3.6 Wilcoxon秩和檢驗

秩和檢驗又稱為維爾克松兩樣本檢驗，是一種非參數統計檢驗。可以作為算法性能的評價指標之一，用于驗證算法之間是否存在顯著差異。本文基于上文的16個基準測試函數，采用顯著水平p=5%情況下的秩和檢驗對LHCOOT算法與6種原啟發式算法(PSO、SSA、GJO、NDFCOOT、COOTTLCR、COOT)進行差異性檢驗。當p<5%時，記為“+”，表示LHCOOT算法優于對比算法；當p>5%時，記為“-”，表示LHCOOT算法劣于對比算法；當p為“NaN”時，表示不適應于顯著性判斷，LHCOOT算法顯著性與對比算法相近。對比結果見表4，在各算法對比中，大多數的秩和檢驗p值小于顯著水平5%，表示LHCOOT算法整體上與其它算法具有顯著性差異，即LHCOOT算法具有更好的尋優性能。

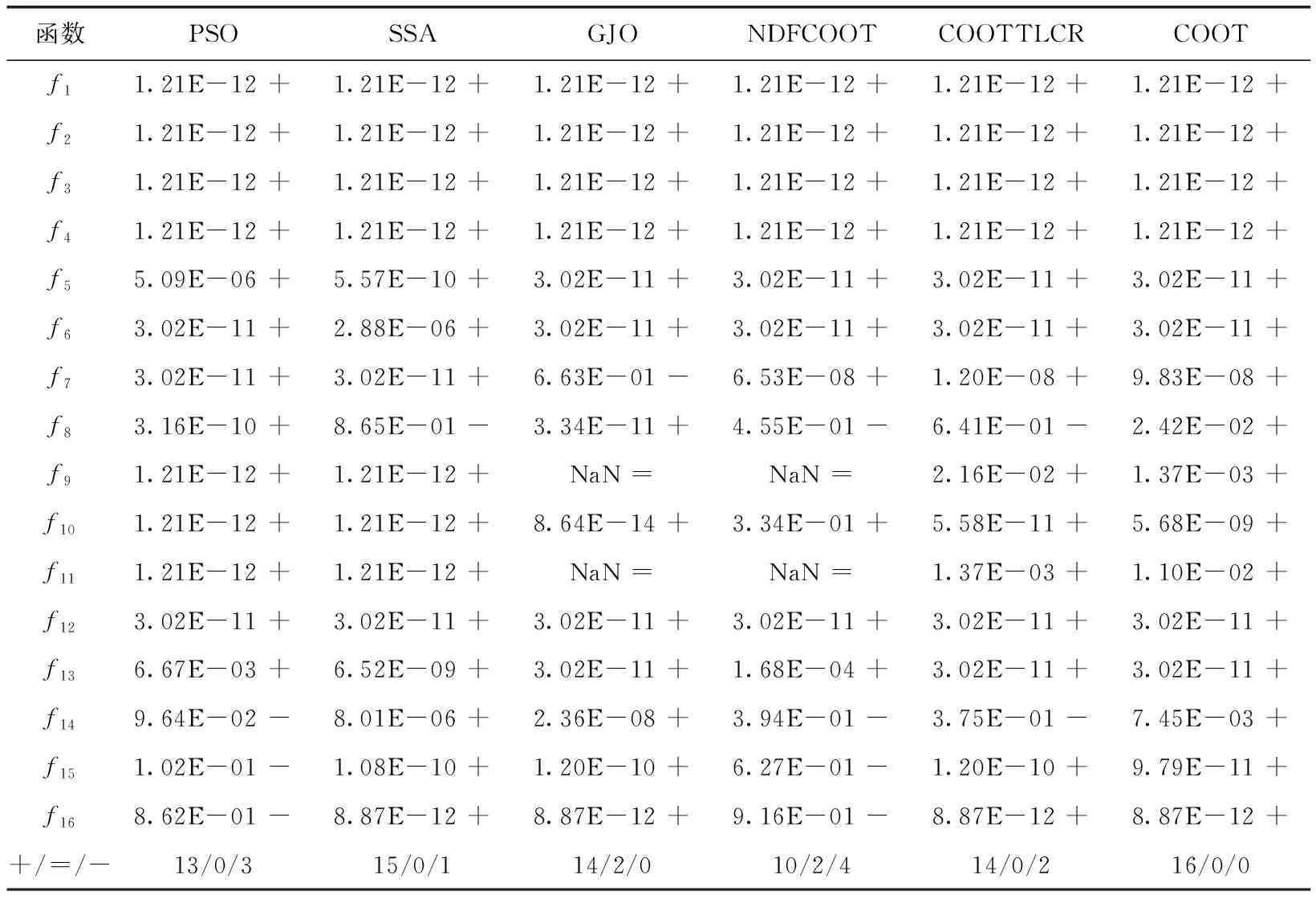
表4 秩和檢驗p值

4 工程問題應用分析

為進一步驗證LHCOOT算法在處理實際工程優化問題的可行性和有效性。本節使用標準焊接梁設計問題作為參考驗證。

焊接梁設計問題屬于典型的非線性規劃問題。在滿足設計變量的邊界條件和剪切應力τ、彎曲應力σ、梁條屈曲載荷Pc、末端偏差δ這4個工程約束指標下盡可能降低焊接梁設計的制造成本。本節采用死刑懲罰函數機制作為非線性約束[19]。4個設計變量分別是焊縫寬度h、橫梁長度l、高度d和厚度b。

設計變量如式(15)所示

x=[x1，x2，x3，x4]=[h，l，d，b]

(15)

目標函數如式(16)所示

(16)

約束條件如式(17)所示

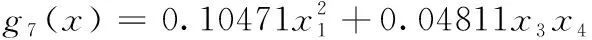
(17)

式中：τmax=136000 psi，σmax=3000 psi，δmax=0.25 in，P、L、E、G為焊接梁問題工程常量，P=6000 lb，L=14 in，E=3×106psi，G=1.2×107psi。psi：磅平方英寸，lb：磅，in：英尺。

表5統計了LHCOOT算法與粒子群算法(PSO)、算數優化算法(arithmetic optimization algorithm，AOA)[10]、海洋捕食者算法(marine predators algorithm，MPA)[20]、金豺優化算法(GJO)[4]、斑點鬣狗優化算法(spotted hyena optimizer，SHO)、變色龍群算法(chameleon swarm algorithm，CSA)[21]在求解焊接梁設計問題的4個設計變量和制造成本。從表中可以看出，LHCOOT算法的焊接梁制造成本最低，說明LHCOOT算法在求解此類工程問題的尋優精度較高，進一步驗證了算法在實際應用中的優越性。

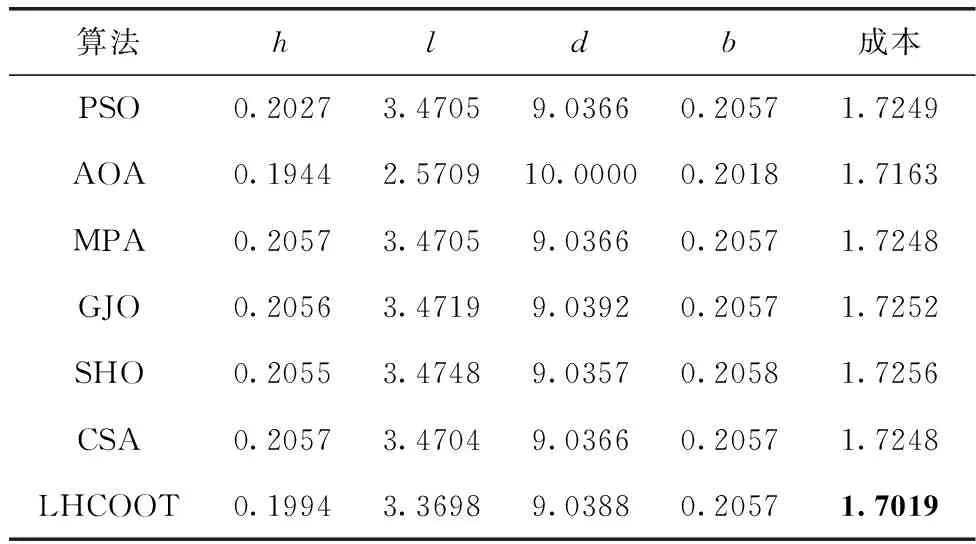
表5 焊接梁設計問題仿真結果

5 結束語

針對COOT算法的尋優精度低，易陷入局部最優等問題，提出了基于拉丁超立方體的改進白骨頂雞算法。利用拉丁超立方體抽樣使白骨頂雞初始種群更加均勻化；引入非線性決策因子和自適應動態邊界的混合位置更新策略以完善3種運動的執行機制，權衡算法全局搜索和局部開發過程；最后引入柯西變異和貪婪策略對最優位置進行擾動，避免算法過早收斂。通過對16個基準測試函數、部分高維函數以及算法秩和檢驗的實驗，表明LHCOOT算法在收斂速度、收斂精度以及逃離局部最優的能力均有了不同程度的提升。通過實際工程優化問題驗證算法在解決工程問題上的可行性。在下一步工作中，將考慮把算法應用到深度學習領域，結合神經網絡進行風電功率的短期預測[22]，拓展算法的實用價值。