基于5G 綠色寬帶通信的能效資源分配優化方法研究

趙靜

(中國廣電青海網絡股份有限公司,西寧 810000)

0 引言

大數據時代通信技術[1,2]的發展都意味著網絡數據傳輸速度要求越來越高,網絡速度越來越快,這對網絡系統性能提出了更高的要求。因此,需要進一步提高網絡系統性能,特別是合理解決系統在運行期間存在資源分配和能耗問題[3]。

隨著無線網絡控制遠程對象技術的快速發展和5G 技術的支持,5G 技術[4]在頻率利用率、能效、資源利用率和數據傳輸速度等方面都有了很大的提高,密集基站將進一步增加網絡覆蓋率,極大地改善用戶體驗。目前,通信技術的優化[5]是以最大吞吐量或最小系統能耗為目標函數,合理分配系統資源,實現系統資源的合理利用。對于5G 時代的綠色通信而言,最重要的是系統能效。因此,構建基于最大化系統能量效率的目標函數是資源分配的主要問題。

許多學者對5G 資源分配問題進行了研究。文獻[6]提出基于馬氏決策的5G 網絡切片虛擬資源分配方法。該方法結合貝爾曼方程及馬氏決策過程的動態規劃迭代算法求解出運營商最優收益解和網絡資源有效利用率。文獻[7]針對單小區多用戶上行大規模MIMO 通信系統,提出了采用分式規劃理論得到最佳基站天線數優化問題。上述文獻大部分研究以大規模MIMO 通信為基礎,然而很少有研究對下行鏈路系統的能效優化進行深入的理論及優化問題研究。此外,部分方法集中解決優化算法尋優問題,然而隨著網絡系統能效優化和資源分配技術的不斷發展,簡單的優化問題已無法適應網絡復雜性要求。

為改善上述問題,本研究結合了寬帶無線通信系統的分析,以優化跨層和跨頻帶無線通信系統中的能量效率。

1 MIMO-OFDMA 建模

本研究以典型的多天線用戶多輸入多輸出-正交頻分多址(Multiple-Input Multiple-Output-Orthogonal Frequency Division Multiple Access,MIMO-OFDMA)[8,9]無線通信系統為例。首先,假定網絡系統中的基站配置的信號傳輸天線共有M個。同時,可通過單個天線連接到基站的K個位置。假設系統運行中總共N個子載波可劃分為V個頻率塊,這些頻率塊是通信系統中資源調度的最小單位。結合網絡系統的信道互易性,上行鏈路信道矩陣Gv計算如下:

式中:Hv——頻率塊上用戶到基站的快衰減矩陣;D——K×K對角陣;diag{·}——對角矩陣;βk——來自基站的慢衰減系數。

基于以上分析,可以知道用戶接收的信號將受到多重干擾,并且多個用戶之間的信號可能相互干擾。因此,這些相互干擾需要通過迫零算法[10]消除預編碼矩陣Fv=[Fv,1,Fv,2,…,Fv,K],因此有:

接著,用戶k第v個頻率塊的總信號矩陣rv,k可以表示如下:

綜上所述,在胃癌根治術中,應用單純全麻,會使患者的應激反應增強,不利于醫護人員的手術操作,全麻藥物作用量大,且術后患者會有明顯的疼痛癥狀產生,而應用全麻聯合硬膜外麻醉可以雙向的阻滯受傷區域的神經感受器傳導及中樞神經的敏感度,從而降低患者的術后疼痛及不良反應,同時術中能夠減少茶氨酚的釋放,降低患者應激反應,使循環系統趨于穩定,有利于手術的順利進行[3]。并且全麻聯合硬膜外麻醉的藥物使用靈活,用量少,易控制患者的應激反應,有利于降低患者的術后疼痛,提高了患者的滿意度,有臨床推廣的價值。

式中:E{·}——期望;W——信號增益;N0——噪聲密度。

根據式(7),用戶在第v個頻率塊中接收的信號的頻率的下限計算如下:

式中:E{tr[·]}——追跡;K——頻率塊的數量;M——用戶數量。

結合式(8)至式(10),用戶k第v個頻率塊的總信號矩陣rv,k(式(7))可簡化為

根據以上分析,用戶在單個頻率塊上的分配率與用戶的大規模衰減密切相關。因此,通過用戶k分配獲得的信號可以計算如下

式中:mk——用戶k分配的頻率塊的數量;pk——用戶k在mk個頻率塊中的任何一個分配中的功率。

系統中能量效率函數U的下限可以表示為

式中:pc——單個頻率塊的固定功率消耗。

根據以上分析,下行鏈路用戶中的大規模MIMO-OFDMA 系統的能效資源分配中的最大化問題可以表示如下

式中:U(·)——能效資源分配目標函數;P——傳輸功率;m——分配給用戶的頻率塊號;Rmin——用戶的最小速率約束;V——頻率塊的總數。

2 能效資源分配模型

本研究提出了基于最小速率要求的能效最大化資源分配算法。主要思路為在合理分配帶寬后,分配功率和天線數量,以提高系統的最佳能效。該算法首先使用用戶接收的平均信噪比和比特率作為參數來計算用戶獲得的副載波數。帶寬分配目標函數mk的優化過程可以表示如下:

為了滿足系統運行期間的最小用戶速率要求,需要首先分配和處理帶寬。帶寬分配算法可描述如下:

從形式上看,能效函數是一種分數形式,因此能效函數需要首先進行處理,使其成為減法形式,然后將其轉化為凸優化問題[11]。為此,目標函數可以表示為

約束定義如下:

令中間變量f滿足式(21):

式中:P——發射功率;M——基站天線數。

結合式(21),f的海賽矩陣H(f)可定義如下:

根據式(22),H(f)是一個負定矩陣,故函數f是一個凹函數。為此,可基于拉格朗日函數[12]將目標函數可以轉換為凸優化問題,具體描述如下:

式中:λk——與約束相對應的拉格朗日乘數。

式(19)能效目標函數的對偶目標函數定義為

當給定λ并且采用KKT 條件時,最佳發射功率P*和基站天線數量M*可以計算如下:

拉格朗日乘數λ可通過以下遞歸公式獲得:

式中:δ——迭代次數;j——迭代步長。

3 試驗與分析

以相對常見的典型無線通信網絡為例進行試驗與分析。案例模擬小區最大覆蓋范圍為1 000 m,用戶以基站為中心隨機分布在100 m 范圍內。為了驗證所提算法優越性,對比了基于NSGA-Ⅱ[13]的帶寬分配算法以及基于分式規劃[8](Fractional planning,FP)的基站天線數量分配算法的性能。對比指標分別選取不同的低速率要求時系統的能效、用戶的吞吐量性以及最佳基站天線數。

用戶數量與系統能效分析結果如圖1 所示。可以看出,與基于NSGA-Ⅱ算法和基于FP 算法相比,所提出的算法能效較高。當用戶數量為20 人時,所提算法能效較NSGA-Ⅱ和FP 算法高約1.64和2.25 倍;當用戶數量為50 人時,所提算法能效較NSGA-Ⅱ和FP 算法高約1.67 和2.5 倍。此外,當用戶數量持續增加時,系統總能效隨著用戶數量的增加而逐漸減少。

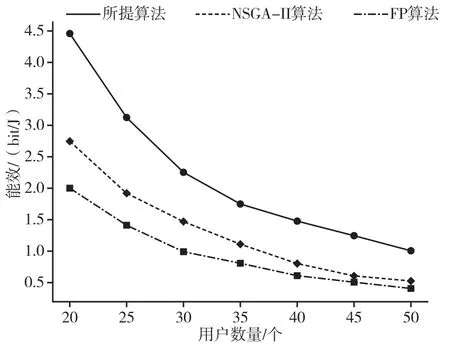
圖1 用戶數量與系統能效分析結果圖Fig.1 Analysis results of user quantity and system energy efficiency

不同數量用戶的吞吐量性能變化如圖2 所示。可以看出,FP、NSGA-II 以及所提出的算法均隨著用戶數量提升系統吞吐量增加,即用戶數量與吞吐量呈正相關性。然而,所提出的算法與FP 和NSGA-II相比,吞吐量提升更加明顯。例如當用戶數量為50個時,所提出的算法較FP 和NSGA-II 相比提升約18.3%和11.9%。分析原因,基于NSGA-Ⅱ的帶寬分配算法中未對用戶速率提出任何要求,并且只要求最大化系統的能量效率,這導致了較低的系統吞吐量。基于FP 的基站天線數量分配算法通過最小化發射功率來分配帶寬,因此與所提出的算法相比,基于FP 算法具有更低的能效性能。此外,當用戶數量持續增加時,系統吞吐量呈現上升趨勢,即隨著用戶數量的增加,系統的多用戶多樣性特征變得更加明顯。

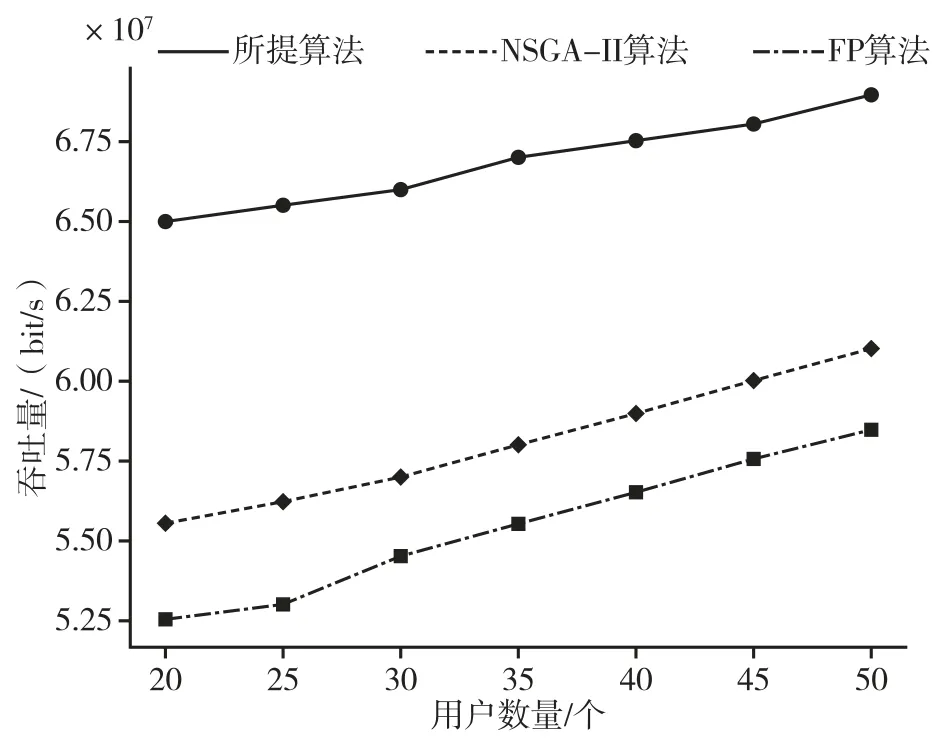
圖2 不同數量用戶的吞吐量性能變化圖Fig.2 Throughput performance changes for different numbers of users

不同用戶數條件下各算法的最佳基站天線數的性能如圖3 所示。可以看出,當用戶數量呈上升趨勢時,系統的最佳基站天線數量也呈上升趨勢。此外,FP、NSGA-II 以及所提出的算法性能相近,差異不是很大。試驗結果表明FP、NSGA-II 以及所提出的算法需要的最佳基站天線數大致相同。然而綜合系統能效和吞吐量分析結果,所提算法綜合性能較為優異。試驗結果進一步驗證了所提模型的有效性及實用性。

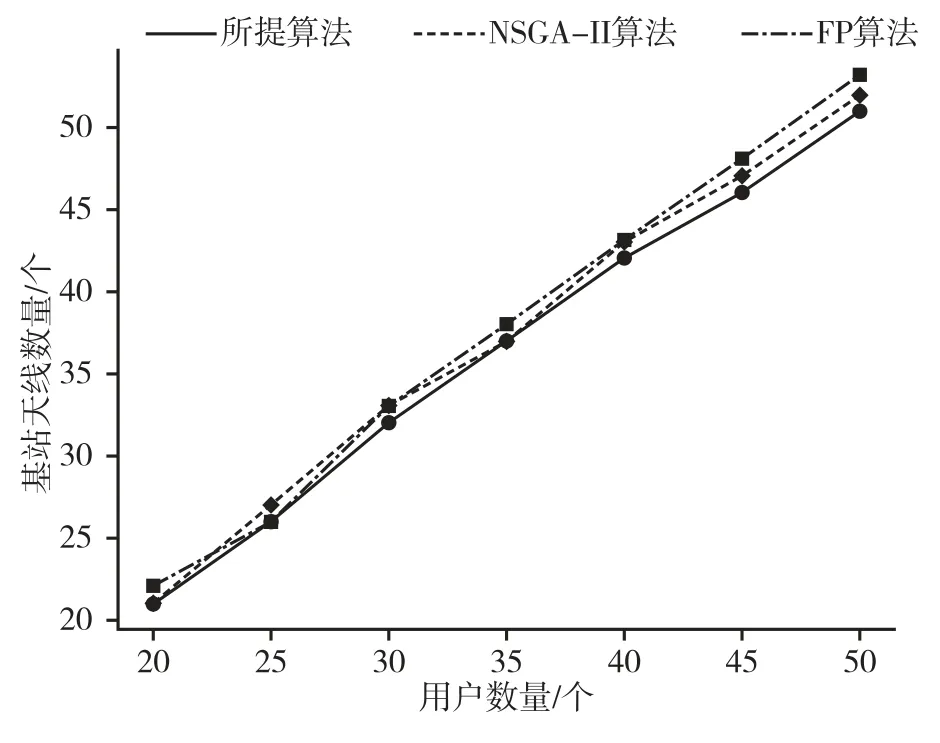
圖3 不同用戶數條件下各算法的最佳基站天線數的性能圖Fig.3 Performance of the optimal number of base station antennas for each algorithm under different user numbers

4 結束語

對多天線用戶MIMO-OFDMA 無線通信系統進行分析,建立了基于最小速率要求的能效最大化資源分配算法。主要思路為在合理分配帶寬后,分配功率和天線數量,以提高系統的最佳能效。該模型為5G 系統安全管理及穩定運行提供了一定借鑒作用。未來可對混合系統參數的優化配置和規模進行研究,從而進一步降低系統總成本。