兼顧電纜線路效率和可靠性的載流量動態閾值研究

王金陽，李海鋒，蘇金躍，王智東*，胡冉,2，葉文忠

（1.華南理工大學電力學院，廣州 510641； 2.深圳供電局有限公司，深圳 518000；3.深圳市壹電電力技術有限公司，深圳 518101）

引言

近年來，城市建設與電力建設的矛盾日益加劇，特別是電力線路走廊的選取越來越難，如何挖掘潛在的容量資源，在提高單位電纜及電力網絡供電能力的前提下，保證電網的安全可靠運行是一大挑戰[1-3]。

當前電纜載流量多根據IEC 60287 標準，假定最惡劣工況下導體溫度90 ℃時，以所計算出的最大允許安全運行載流值作為閾值。由于該閾值固定，而在實際中電纜的外部環境并不相同，與真實閾值必然存在一定偏差，若該閾值相對真實閾值過低，容易導致誤報警的情況，降低線路的運行可靠性；若該閾值相對真實閾值過高，則沒有充分發揮電纜的真正供電能力，浪費了電網資源[4-7]。

針對上述問題，本文提出了一種兼顧電纜線路效率和可靠性的載流量動態閾值研究方法，基于電纜載流量與導體溫度的機理關系分析，將不同位置、不同環境下的電纜線路的固定閾值動態化，通過該動態化閾值幫助運維人員對電纜線路管理決策，在保證電纜線路可靠性的基礎上提高其利用率。

1 載流量變化影響分析

1.1 理論分析

當前電纜的載流量閾值的理論計算參考于標準中的計算公式，基于導體溫度與運行載流量的相關關系來得出單一固定閾值。而電纜在日常運行中，難免出現過載過應急供電等工況，此時劇烈的載流量變化會導致電纜導體溫度的異常升溫，若閾值固定，將降低電纜運行的可靠性。載流量與導體溫度的變化機理復雜，影響因素也包含了周圍土壤溫濕度、散熱條件等外部因素，要保證線路可靠運行的前提是對電纜的載流量與導體溫度的相關關系進行具體分析，以得出兩者的定性關系來替代定量關系。

電纜載流量的計算公式可根據溫度場微分方程求解得到，經微分方程簡化可得單芯電纜運行時的梯狀熱路如圖1 所示。

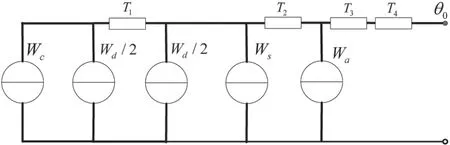
圖1 穩態額定載流量計算梯狀熱路圖

圖1中，Wc為電纜導體單位長度損耗，Wc=I2R，Wd 為導體絕緣單位長度的介質損耗，Ws為電纜金屬套單位長度損耗，Wa為電纜鎧裝層單位長度損耗，T1為導體與金屬套之間單位長度熱阻，T2為金屬套和鎧裝層之間內襯層單位長度熱阻，T3為電纜外護層單位長度熱阻，T4為電纜表面和周圍介質之間單位長度熱阻，θ0為光纖測得的電纜表面溫度。

土壤直埋電纜的額定載流量計算公式如下：

式中：

n—電纜中載有負荷的導體數；

λ1—電纜金屬套損耗相對于所有導體總損耗的比率；

λ2—電纜鎧裝層損耗相對于所有導體總損耗的比率；

I—載流量；

R—導體單位長度的電阻；

?θ—電纜導體溫度相對于環境溫度的溫升。

綜上理論分析，因結構層之間的計算熱阻為參數，可根據實際測取，故電纜線路的載流量計算主要將導體的溫升看為變量進行分析。而整條電纜線路各位置上的參數并不一致，如熱阻T4的測定與土壤熱阻系數、散熱系數等因素有關，相同載流量下的電纜各位置導體溫度有高溫點也有低溫點，很難測定一個作為所有位置的基準值來計算電纜載流量。結合上述考慮，又因電纜整條線路上采樣位置點過多，且周圍環境變化無常，難以實現各位置點的參數均精確測定。因此，本文將公式（1）簡化為電纜載流量與導體溫度θ的函數式如公式（2）所示，結合工程中的歷史數據，參照各位置點的導體溫度大小來選定系數β來為函數式進行校正。

1.2 實際工程分析

在理論分析的基礎上，本文以某電網中實際運行的電纜工程的實測數據進一步分析電纜載流量與導體溫度的函數關系以及系數β的取值。圖2 為電纜線路一天中載流量最大時刻與最小時刻的各位置采樣點的溫度大小，圖中數據顯示整條線路上的各采樣點溫度明顯不同，存在高低起伏的情況，但線路電流的大小同樣影響整條線路導體溫度大小，反映在數據上則為大電流相對于小電流整體抬高了導體溫度曲線。進一步地，數據表明存在一條基準導體溫度曲線，輔以系數β的不同取值，隨電流的大小變化，即可代表該電纜各個位置點在某一時刻實時載流量下導體溫度的變化情況。

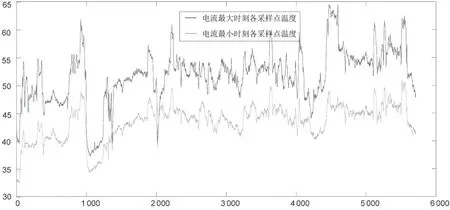
圖2 電流最大與最小時刻電纜線路各位置點導體溫度變化曲線圖

考慮到城市配網中電纜線路的電流變化具有一定周期性，一般來說凌晨時段為一天中的電流低時段。因此，本文取一天中零點零分時，整條線路各位置點的導體溫度曲線作為基準曲線，此時刻的電流作為基準電流I0，系數β的取值計算為：

2 載流量動態閾值分析

基于理論與實際工程分析，可在載流量與導體溫度的函數關系式的基礎上加上基準閾值，以實現載流量的閾值動態化，并保證線路在導體溫度在90 ℃的情況下，載流量閾值盡可能的大。本文定義電纜線路的動態閾值如下：

式中：

THk—電纜k 位置點的載流量動態閾值；

α—基準閾值，大小取決于外部環境的優劣；

f(θ)—載流量與導體溫度的函數關系式，隨著導體溫度變化，載流量閾值隨之動態變化。

2.1 基準閾值取值方法

基準載流量閾值α用以表征電纜線路局部的外部環境特征，取值基于同一載流量下的各位置點導體溫度。下圖3 為實際電纜線路工程任取的8 個采樣位置點溫度及電流的全天變化曲線，從一天中各位置點的導體溫度變化曲線上分析，各條曲線波形基本一致，只存在數值上的高低差異，因此在同一載流量下，導體溫度的大小受外部環境的差異影響。

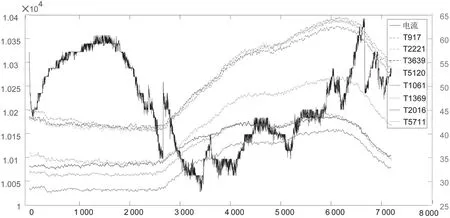
圖3 典型采樣點與電流的全天變化曲線圖

基于實際工程所得數據，本文基準閾值α的計算原則為：在歷史數據上抽取各個位置點的平均溫度，評估各個位置點導體溫度的基礎閾值，再通過導體溫度與載流量的相關計算關系，從而得到載流量動態閾值的基準閾值α。

2.2 動態閾值計算方法

綜合上述分析，電纜線路載流量閾值隨導體溫度變化同樣在變化之中，為替代電纜線路傳統方法所使用的固定閾值，本文在實際電纜線路工程采集到載流量、導體溫度數據的基礎上，結合兩者函數關系式，以及表征不同外部環境的基準閾值，計算得出電纜線路的動態閾值，計算方法具體流程圖如圖4 所示。

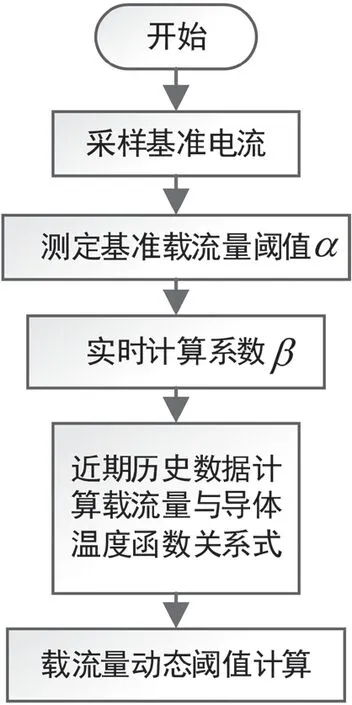
圖4 動態閾值計算流程圖

首先，由所采集到的載流量、導體溫度數據取定基準電流I0和基準載流量閾值α，再引入載流量與導體溫度的函數關系式（2），實時計算系數β，然后通過電纜線路歷史數據代入式（2），由此得到電纜線路的動態閾值。

3 應用算例

本文所研究的載流量動態閾值方法已應用于實際電纜線路工程中，電流數據通過電流互感器采樣至采集模塊，導體溫度通過內置的測溫光纖采樣至測溫模塊，數據實時上傳至智能電纜測控終端，測控終端與數據中心及智能運維管理平臺信息雙向傳遞，及時做出決策調控。智能電纜系統測控終端結構圖如圖5 所示。

圖5 測控終端結構圖

測控終端所測得的數據，經網絡端口傳輸到數據中心后，在動態閾值與運行電流模塊中。功能模塊界面上將各條線路的名稱、輸送負荷、動態閾值、各相位的實時載流量、線路平均電壓等信息以數字形式顯示。

基于本文算法計算結果及整體界面如圖6 所示，電流動態載流量閾值顯示在紅色框中。三條線路其中一條輸送負荷高，一條輸送負荷低，備用線路未啟用，不承擔輸電任務。未供電線路相比于帶負荷線路動態閾值設置為初始值1 000 A；高負荷線路與低負荷線路兩條線路相比，由于敷設環境、外部氣象條件、散熱條件、土壤溫濕度等因素不同，所計算得到的各自線路動態閾值同樣存在高低。

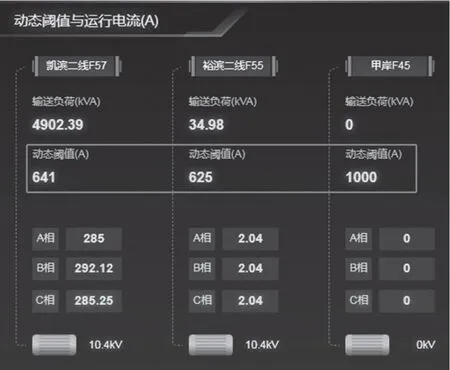
圖6 動態閾值與運行電流的歷史數據查詢分析圖

4 結語

為提高電纜運行可靠性，本文基于對電纜的載流量與導體溫度的相關函數關系，測定線路的基準閾值后，用基礎閾值和帶系數的動態函數來表征載流量的動態變化，以動態閾值算法來動態管控電纜運行狀態。本文算法應用于目前在運的實際電纜線路工程中實現動態閾值模塊功能，測控系統數據驗證了本文算法的有效性。