無人駕駛項目CC-TCMS通信中斷場景探討及優化

夏振東，胡 歡

（卡斯柯信號有限公司，北京 100070）

隨著軌道交通行業的不斷發展，無人駕駛項目已先后在多個城市投入運營，并且多地正有條不紊的推進著無人駕駛項目的建設，無人駕駛和車-車通信已經成為當今軌道交通行業的熱點。無人駕駛項目在場景文件中描述了全自動運行系統在運營中所要處理的場景，包括正常運營場景和非正常運營場景，所描述的對象涉及組成全自動運行整個體系所包含的（子）系統和人員。各個系統遵循場景文件執行，是保障無人駕駛項目功能實現的前提。本文就無人駕駛項目可能會遇到的CC 與TCMS 通信中斷的故障場景，論述既有項目此種場景下的處理方式，并基于現有處理機制提出優化建議。

1 FAO項目當前處理及分析

對于CC 與TCMS 通信中斷后的處理方式，筆者對比了北京的《城市軌道交通全自動運行系統規范》（T/CAMET 04017.1-2019)以及上海的《城市軌道交通全自動運行運營場景規范》（T/SHJX0018-2020），兩者的處理方式基本一致。

總結如下：當車載監督與車輛TCMS 通信的報文時，若超過規定時間未接收到車輛TCMS 報文，則認為與車輛TCMS 通信故障。

系統處理方式如下：

1）若列車處于非零速，施加緊急制動，車停下后由信號向中心申請進入蠕動模式(Creep Automatic Mode，CAM)，中心進行確認后，列車進入蠕動模式，以既定的限速運行到下一站進行清客操作。

2）若列車處于零速，則直接向中心申請進入蠕動模式，中心授權后方可進入蠕動。

以上處理方式，存在如下問題：

1）由于不區分車速，只要非零速，當CC 與TCMS 通信中斷后，一律施加緊急制動。因此在沒有提前廣播告知的情況下，突然施加緊急制動易造成乘客受傷，給乘客帶來不好的出行體驗。

2）蠕動模式屬于降級后的FAO，為保障安全，因此該模式限速很低，非必要過早地進入蠕動模式，會大大降低運營效率。

2 處理方式優化

筆者認為針對CC 與TCMS 通信中斷這一場景，不考慮CC 判斷與TCMS 失去通信的過程（不同項目有不同的定義）及CC 和TCMS 的時延。當CC已經判斷與TCMS 失去通信后，可根據列車所在位置不同，進行不同的處理。本文按以下3 種情況分別論述。

2.1 列車離站過程中的優化處理方式

如圖1 所示，當列車在出站過程中出現CC 與TCMS 通信中斷的情況，當車已離開站臺D距離后，信號不處理，讓車進入區間。當車離開站臺，運行距離小于D時，信號輸出緊急制動，讓乘客可以盡早完成疏散，司機/維護人員可提早人工對故障車進行干預。

圖1 列車離站Fig.1 Train departure

對于列車離站過程中CC 與TCMS 通信中斷的處理方式，需確保在距離D內列車施加緊急制動，車停下后至少有一個門仍在站臺區域里。因此從疏散角度結合車輛參數（車門到車端距離等）和停車點到站臺邊緣的距離進行分析，列車從啟動到緊急制動停車的走行距離需滿足如下關系，如公式（1）所示。

車長：取自車輛參數。

停車點（SSP）到站臺邊緣距離：通過平面圖數據獲取，取最小值。

最小疏散距離：考慮車輛參數中第一個客室門中心到車端的距離及停車點到站臺邊緣的最小距離，因此最小疏散距離＝2×車端到第一客室門中心距離＋停車點（SSP）到站臺邊緣距離。

本文引用某開通項目的具體參數進行計算，引用參數如表1 所示。

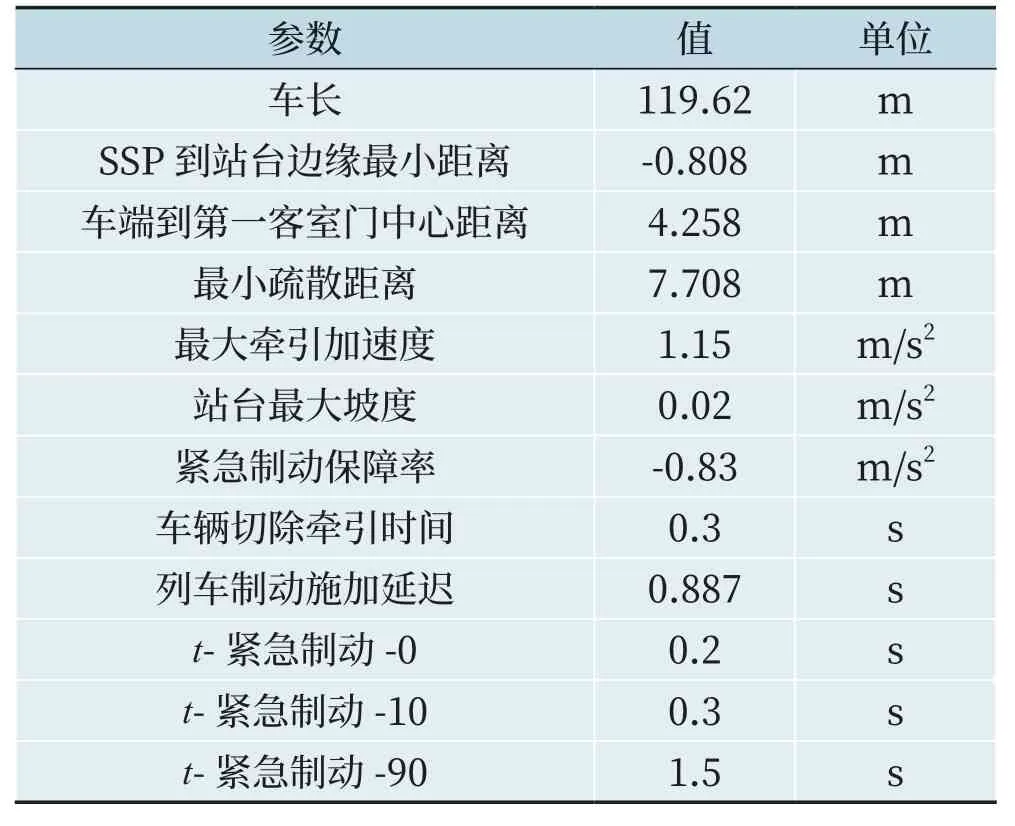
表1 引用參數Tab.1 Reference parameters

因此，總走行距離S＝車長＋停車點到站臺邊緣距離－最小疏散距離＝119.62 m－0.808 m－7.708 m ≈111.1 m。

從整個運動過程來看，考慮最壞的情況，列車以最大牽引加速度（考慮站臺最大下坡）從站臺發車，到達距離D時觸發緊急制動，隨后以緊急制動保障率的減速度（GEBR）進行停車。因此總走行距離S＝D＋緊急制動距離，若要求得距離D，只需求得列車EB 后走行的的距離即可。

對距離D計算過程如下（為方便計算所有計算結果均保留小數點后三位）：

在《CBTC 系統性能和功能要求》（IEEEl474- 1）標準中，為CBTC 模式下列車緊急制動防護模型定義了“典型安全制動速度-距離曲線”，如圖2 所示。引入由于列車定位的不確定性(考慮前車定位誤差及系統允許范圍內可能的退行距離)產生的誤差。最外層曲線為該模型下列車不可突破的制動曲線。

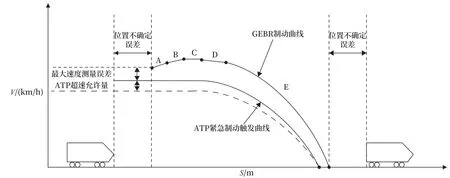
圖2 安全制動模型示意Fig.2 Schematic diagram of safety braking model

根據《CBTC 系統性能和功能要求》（IEEE l474-1）標準，可以將緊急制動過程劃分為3 個階段進行評估，如圖3 所示。

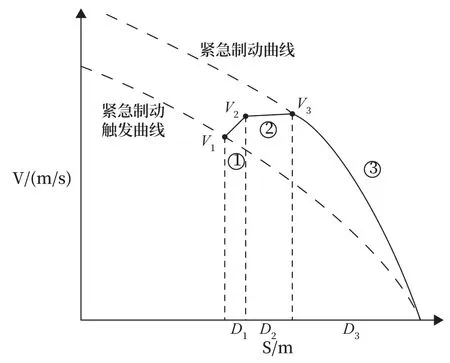
圖3 緊急制動等效模型Fig.3 Emergency braking equivalent model

第一階段，是車載ATP 系統響應階段對應圖2中的A、B，車載ATP 從檢測到緊急制動發生，并觸發緊急制動到車輛切除牽引的一段過程。在該階段t1時間內列車被估算以最大可能的加速度（車輛牽引產生的最大加速度與線路坡度產生的加速度之和）運行。

第二階段，是車從牽引切除到達到緊急制動保障率的90%的過程，對應圖2 中的C、D 過程。對應運行距離、加速度及時間分別為D2、a2，t2；從信號車輛接口電路設計上看，由于車輛牽引切除命令及緊急制動施加命令均采集列車緊急制動環路，因此車輛牽引切除時間與緊急制動施加時間可能有部分重疊。從設計安全角度考慮，在牽引切除過程中應不考慮施加制動的影響。第二階段的時間t2在時序上應嚴格滯后于第一階段時間t1。

根據《列車制動系統性能規范》（EN13452-1），按照如圖4 所示等效模型時間參數定義t2的等效延時為te，即通過車輛參數t10和t90計算等效中值te。此時，列車處于惰行狀態，安全計算中列車應使用線路坡度產生的最大加速度aslope。

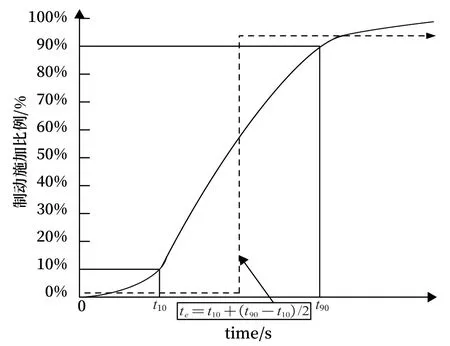
圖4 等效惰行延時Fig.4 Equivalent coasting delay

第三階段是從緊急制動保障率90%的制動施加到列車完全停止的過程。對應圖2 中的E 過程。此階段對應運行距離，加速度及時間分別為D3、a3，t3；本階段列車處于緊急制動保障率GEBR 施加狀態下的全減速狀態。

緊急制動3 個階段對應的運行距離、速度、加速度及時間對應關系如圖5 所示。

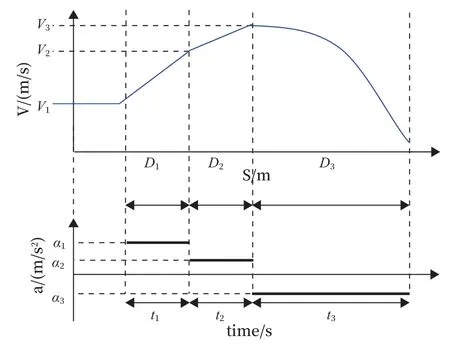
圖5 緊急制動模型參數對應關系Fig.5 Corresponding relationship of parameters of emergency braking model

第一階段中ATP 檢測到緊急制動從而進行牽引切除，此階段列車以最大加速度a1＝1.17 m/s2考慮站臺最大坡度加速度為0.02（m/s2）運行，持續時間t1＝1.29 s（考慮系統響應延時及和車輛切除牽引的時間）。根據運動學公式，計算如公式（2）所示。

其中：s表示走行距離；v0表示初速度；t表示時間；a表示加速度。

將相應量帶入公式（2），對應運行距離D1＝V1×t1＋0.5×a1×t12，代入已知數值可得D1＝1.29×V1＋0.973。

第二階段運動相當于惰行階段，此階段的時間根據等效惰行延時t2＝te＝（t10＋t90）/2 ＝0.9（s），考慮站臺最大坡度加速度為0.02 m/s2，因此此時的最大加速度為a2＝0.02 m/s2，根據運動學公式（2），帶入相關量后，運行距離D2＝V2×t2＋0.5×a2×t22＝（V1＋a1×t1）×t2＋0.5×a2×t22，代入已知數值可得，D2＝0.9×V1＋1.366。

第三階段實際是列車以最小緊急制動aGEBR（即緊急制動保障率GEBR）與線路坡度產生的最大加速度aslope之和，進行勻減速運動停車。通過參數表可知a3＝aGEBR＋aslope＝-0.81 m/s2，根據運動學公式，計算如公式（3）所示。

注：V0：初速度；Vt：末速度；s：走形距離；a：減速度（制動過程）。

將相應量帶入公式（3），運行距離可表示為：

根據走行距離關系，S＝D＋D1＋D2＋D3，其中代入數值及表達式可得，0.427×V12＋0.617×V12＋1.885×V1＋1.439 ＋0.9×V1＋1.366 ＋1.29×V1+0.973 ＝111.1，合并同類項后可以得到一個關于V1的一元二次方程，1.044×V12＋4.075×V1－ 107.322 ＝0，根據一元二次方程求根公式，可求得V1＝8.373 m/s，代入可得D＝29.939 m。因此當車出站運行距離在29.939 m 之內，CC 與TCMS 失去通信，列車將施加緊急制動，否則將繼續運行。

2.2 列車區間運行中的優化處理方式

如圖6 所示，當列車在區間運行過程中出現CC與TCMS 通信中斷的情況，此時TCMS 無法接收到信號發出來的牽引制動命令及級位信息。列車受阻力和摩擦力影響自然降速，信號對列車實際車速及參考速度進行監控，具體過程如圖7 所示。

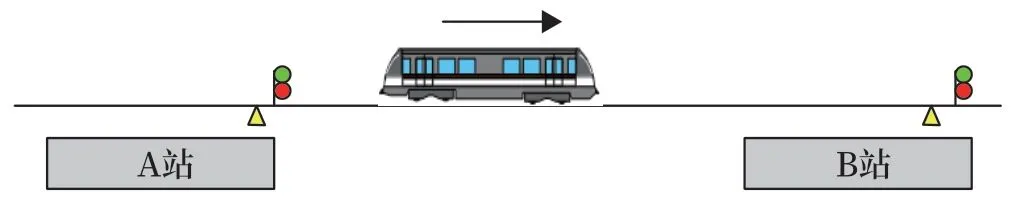
圖6 列車區間運行Fig.6 Train is running in the section

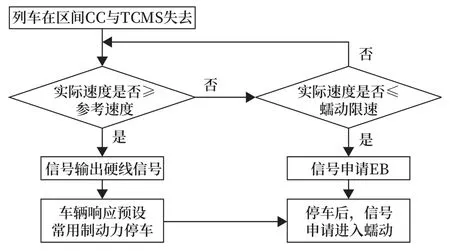
圖7 區間運行處理流程Fig.7 Processing flow chart when train is running in the section

若檢測到實際速度大于等于參考速度時，信號可輸出單獨硬線信號或用CAM_OP（蠕動模式可用）替代，車輛非零速收到此信號后施加預設好的一定級位的常用制動力（如-0.6 m/s2）停車，同時播放預制廣播（如列車將施加制動停車，請扶穩坐好）。停車后向中心申請進入蠕動模式。

若實際速度小于參考速度，且實際速度小于等于蠕動模式既定速度后，車輛播放預制廣播（如列車將施加緊急制動，請扶穩坐好），信號進行干預施加緊急制動，讓列車盡快停下來，隨后向中心申請進入蠕動模式，中心確認后自動進入蠕動模式，運行到下一站完成清客。

注：可能存在限速區域變化（由大變小），同時存在大下坡，列車響應制動存在一定延時，可能會出現超速EB，此時按正常停車后，申請進入蠕動處理。

2.3 列車進站過程中的優化處理方式

如圖8 所示，當列車在即將到站或進站運行過程中出現CC 與TCMS 通信中斷的情況，這時需要確保列車能夠停在站臺，以免發生越站。當列車與站臺區域有交集時，CC 根據當前車速，以及距停車點的距離，并依據緊急制動模型，實時進行判斷。當CC 確保以當前速度緊急制動后，車能夠停在停車點后5 m 內時觸發EB。

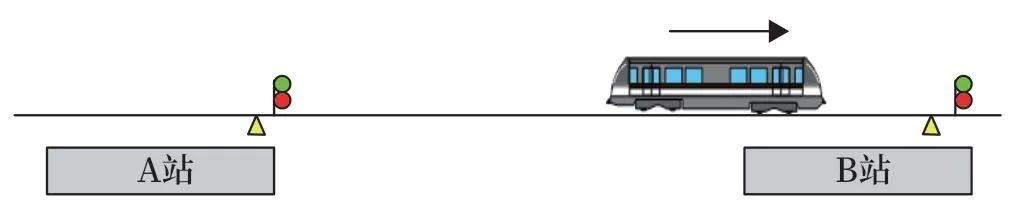
圖8 列車進站過程中Fig.8 In process of train entering the station

根據緊急制動模型，緊急制動觸發速度即為當前車速，緊急制動距離相當于上文中的D1＋D2＋D3，將變量V1替換為當前速度V，站臺區域坡度一般較小，因此統一按表1 中站臺區域坡度計算。代入常量，化簡后的表達式為D1＋D2＋D3＝0.617×V2＋4.075×V＋3.778。

判定條件如表2 所示。

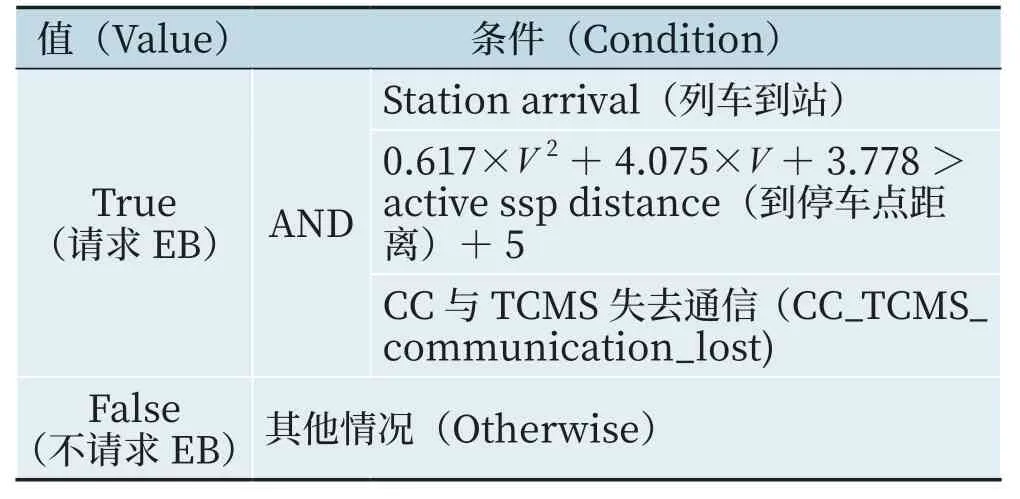
表2 判定條件Tab.2 Determining conditions

增加此判斷的目的是，當車進站過程中由于CC與TCMS 通信中斷，無法正常施加制動，CC 根據車速實時監控是否需要施加EB 確保列車在本站停車不冒進信號機。同時考慮了跳躍的范圍，一旦停車后，正常通過申請進入蠕動模式，在±5 m 范圍內，直接通過跳躍進行對標，對標完成后進行清客處理。

3 結束語

隨著城市軌道交通行業的不斷發展，全自動無人駕駛、互聯互通以及車-車通信（TACS）技術已然成為了行業發展的主流，項目在執行過程中也將面臨更加復雜的場景。在提高自動化程度的同時，如何更大程度上提高乘客出行體驗，當出現異常情況時，如何最大限度減小對運營及乘客出行的影響，是無人駕駛項目需要探究和實現的重要方面。本文通過對CC 與TCMS 通信中斷這一故障場景的系統處理進行分析和探討，給出了筆者認為更加合理的優化方式，希望為后續無人駕駛項目針對此故障場景的系統處理，提供一種新思路。