電火花加工用磁懸浮驅動器控制系統

趙芳　張健　孫鳳　徐方超　欒博然　劉洋　張曉友

摘要：針對傳統電火花加工時，主軸不能及時調整極間間隙導致加工效率低下的問題，提出了一種多自由度磁懸浮驅動器代替傳統電火花主軸運動。分析了該磁懸浮驅動器的結構及原理并建立了磁懸浮驅動器的動力學模型，運用有限元仿真軟件對該驅動器所產生的電磁力進行仿真分析，通過設計傳統PID控制系統及模糊PID控制系統對磁懸浮驅動器的控制效果進行仿真與實驗驗證。結果表明，該磁懸浮驅動器具有較好的跟隨特性和快速的響應速度及符合要求的電磁力，滿足微細電火花加工要求。

關鍵詞：電火花加工；磁懸浮驅動器；動力學模型；電磁力；模糊PID控制；有限元仿真；響應速度；跟隨特性

中圖分類號：TG661 文獻標志碼：A 文章編號：1000-1646（2024）01-0082-09

微細電火花加工是一種非接觸電熱加工工藝，對某些金屬的加工具備若干優點。微細電火花加工技術不僅可以加工特殊和復雜形狀的零件，而且在加工過程中無任何宏觀切削力，但在傳統電火花加工機床上調整工件和電極之間的極間間隙多數采用電機與滾珠絲杠配合而成，受其自身條件影響，在加工過程中難以避免地產生時間滯后、效率低下等問題。對此國內外學者就提高電火花加工效率方面做出了一定的研究。電火花加工效率提升的主要方法包括：電火花放電頻率的增加，針對控制器的使用以及機械結構的改進，還有一部分學者通過改進加工方法來提升電火花加工效率。劉廣民等通過減小電火花加工極間放電脈沖、增大放電間隙探索了一種基于電路共振原理的頻率在30-300MHz的脈沖電源，通過改進電源放電頻次達到提高加工效率的目的。胡波等建立了一種基于極間阻抗特性的微細電火花放電狀態檢測系統，該系統建立在極間阻抗變化特性的基礎上，利用單片機芯片設計檢測系統，使用串口與電源控制模塊通信，實時檢測極間放電狀態并進行反饋，經過測試后，通過建立電火花放電狀態檢測控制系統達到了提高加工效率的目的。FENG等提出了一種具有高響應頻率特性的磁懸浮主軸系統替代原有的機械連接結構，通過在高溫合金上進行鉆孔加工實驗，與傳統加工方式相比，其放電百分比增加30%，進一步提升了加工效率。ZHANG提出了一種在復合能量場下利用旋轉短弧進行高速電火花加工的新方法。通過洛倫茲力、電場力以及工具電極的高速旋轉間共同作用，在電極與工件間產生旋轉的短電弧，以此提升了材料去除率和加工效率。SINGH等驗證了磁場和超聲振動對加工區的聯合作用，使半圓形微特征的材料去除率更高，錐度更小，提升了加工效率。XU等提出了霧化放電加工法，使用氬氣和氧氣霧化介質進行比較實驗，驗證了霧化電火花燒蝕加工效率是傳統電火花加工效率的8倍。NI等研發了一種結合電極振動、旋轉、泵沖洗三種方式的混合旋轉超聲電火花加工系統，實現了更穩定的材料去除率。磁懸浮驅動器作為一種將電磁力轉化為機械力的典型機電系統，具有無機械磨損、無需定期潤滑、減小使用空間等優點，被應用在精密加工、密閉閥體、航空航天等領域。磁懸浮技術是利用懸浮磁力使物體處于一個無摩擦、無接觸懸浮的平衡狀態，通常可控的電磁力不可取代，電磁懸浮是目前市場上應用最廣的一種磁力懸浮方式。

綜上所述，學者們為了提升電火花加工效率，基本都是在改變機械結構或者設計不同的控制器等某一方面來提升電火花加工效率，本文提出了一種多自由度磁懸浮驅動器結構，在此基礎上運用PID和模糊PID控制器設計了磁懸浮驅動器的控制系統，對磁懸浮驅動器進行仿真和實驗研究，分析在不同控制策略下的控制效果。

1 多自由度磁懸浮驅動器裝置

1.1 磁懸浮驅動器工作原理

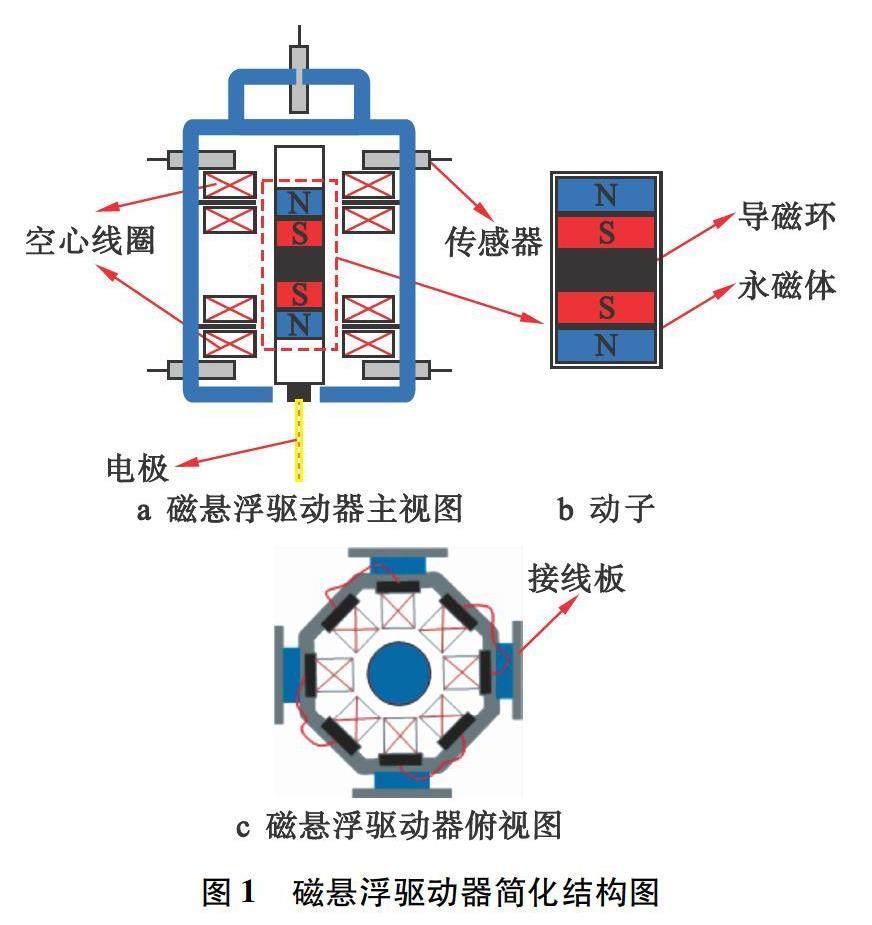
圖1為多自由度磁懸浮驅動器簡化結構模型。該多自由度磁懸浮驅動器主要由空心線圈、動子、位移傳感器組成，其中動子由永磁體和導磁環組成，空心線圈分為上下兩組，每組由8個線圈組成，5個位移傳感器分別負責檢測動子x、y兩個方向的位移以及z方向位移。

根據電磁感應原理，向線圈中分別通人正負電流可以調節空心線圈的N/S極。在實際控制中采用dSPACE的8個D/A輸出口分別控制兩組線圈，進而達到控制動子多自由度運動的目的。磁懸浮驅動器動子位移變化被高精度位移傳感器檢測并輸入到控制系統中，在磁懸浮驅動器位移控制系統中與輸入的期望位移作比較，經比較后將輸出的位移信號轉化為電壓信號，再經過功率放大器輸出到磁懸浮驅動器中進行位移調節。圖2為磁懸浮驅動器z方向移動原理圖。

當線圈與動子間距一定時，隨著電流的增加，電磁力呈現逐漸增大的趨勢，電流為1A時，軸向電磁力為4N，徑向電磁力略高于軸向電磁力。當線圈通入電流大小一定時，隨著動子的平移，電磁力呈現上下波動的趨勢，當動子沿徑向、軸向移動時，0-2mm位移范圍內電磁力大小無明顯變化。

3 多自由度磁懸浮驅動器的動態特性

3.1 磁懸浮驅動器的控制方案

傳統PID控制因其簡單、易調節等特性成為了工業生產領域中使用最多的控制器。本文采用傳統PID控制器來設計磁懸浮位移控制系統，為達到較好的控制效果需要調整好比例、積分、微分3個參數之間的動態變化關系，其數學表達式為

式中：e（t）為系統誤差；kp為比例系數；ki為積分系數；kd為微分函數；G（s）為傳遞函數。對多自由度磁懸浮驅動器進行階躍響應仿真分析，分別對z方向的移動、x方向的平動，以及θ方向的轉動施加初始值為z=0.2mm，x=0.2mm，θ=10mrad的階躍進行仿真測試，通過試湊法在閉環中給定系統一個干擾，記錄過渡曲線，進行比例環節、積分環節、微分環節逐個調節，直到獲得比較理想的控制器參數。z方向kp=43，ki=80，kd=0.45；x方向kp=53，ki=102，kd=0.50；θ方向kp=900，ki=1800，kd=10。仿真結果如圖7-9所示。

由階躍響應仿真結果可知，采用傳統PID磁懸浮控制系統對該多自由度磁懸浮驅動器進行控制時，z方向響應時間為0.029s，調節時間為0.1s，超調量為13.3%；x方向響應時間為0.023s，調節時間為0.19s，超調量為24.6%；θ方向響應時間為0.031s，調節時間為0.17s，超調量為20.3%，該控制系統具有一定超調量和較高響應速度。由于微細電火花加工電極與工件間隙的微小變化，傳統PID控制超調量較大，難以及時調整，無法滿足加工要求。

3.2 模糊PID控制系統

變量較多、結構復雜的系統往往需要進行系統動態簡化，而模糊控制是較為合適的系統簡化方法，由于Mamdani模糊控制系統中不穩定控制對象的動態性能和穩態性能均有較大提高，所以本文采用經典Mamdani模糊控制系統。該磁懸浮驅動器控制系統為多自由度控制系統，故選擇二維模糊控制。二維模糊控制器可以在保證控制精度的同時，避免由于計算規則過于復雜帶來的響應結果滯后問題，由于在傳統PID控制系統中加入了模糊算法，所以比例系數、積分系數、微分系數都是在原有PID控制基礎上加上模糊算法的變化值才能得到最終的修正值，參數修正值計算公式為

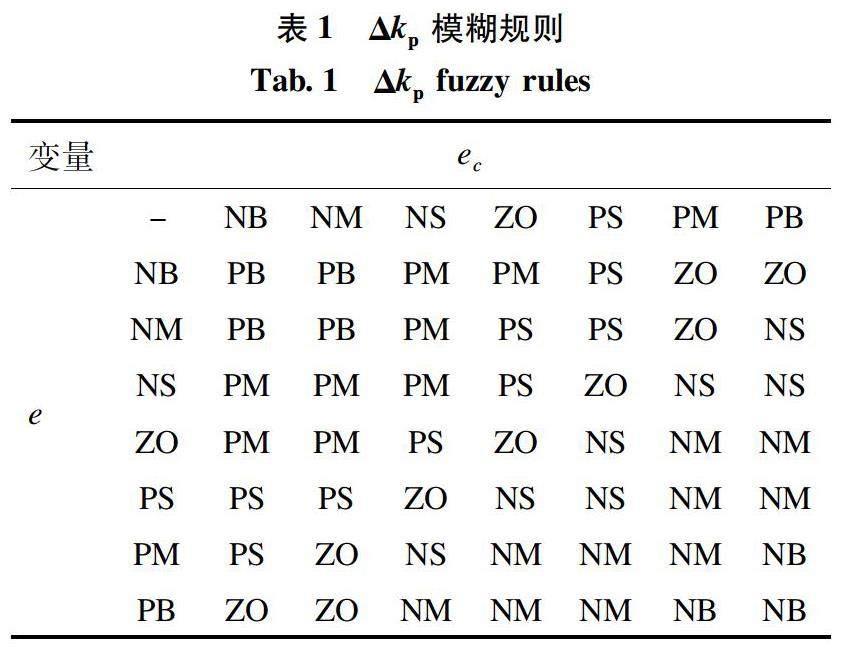
模糊控制系統需要定義NB（負大）、NM（負中）、NS（負小）、ZO（零）、PS（正小）、PM（正中）、PB（正大）7個模糊子集。設置兩個輸出變量為e和ec，論域為[-6，6]。設置3個輸出變量為△kp、△ki、△kd，論域為[-3，3]。因為系統要求響應迅速、靈敏度高，所以模糊系統選擇三角函數作為系統輸入輸出隸屬函數。建立模糊控制規則是模糊PID控制系統的重要部分，根據控制參數的整定原則以及輸入量、輸出量之間的關系來確定輸出變化量△kp、△ki、△kd的模糊規則，結果如表1-3所示。

確立模糊規則之后進行模糊決策及解模糊化處理，常用的解模糊化方法有最大隸屬度法、重心法、取中位數法。重心法又稱為加權平均法，即計算輸出控制范圍內的一系列連續點的重心，而最大隸屬度法一般通過平均值、最大值、最小值3種方法獲得最終結果。為了使計算量化因子和比例因子更加準確，本文選用重心法計算量化因子及比例因子，結果如表4所示。

使用MATLAB輸入以上數據，分別對z、x以及θ自由度進行仿真分析。設定初始位移分別為0.2mm、0.2mm、10mrad，判斷仿真模糊PID控制系統是否符合微細電火花電極與工件極間間隙調節條件，需要在0.2s處向x、z方向施加0.1mm、θ方向施加5mrad的階躍信號。觀測仿真曲線在改變位移條件下的調節效果及響應速度，對比傳統PID控制系統，仿真結果如圖10-12所示。

由仿真圖像可知，設置z方向參考位移為0.2mm時，模糊PID控制的響應時間為0.07s，超調量約為5.3%。當在0.2s后施加0.1mm的位移信號時，再次恢復穩定的調節時間為0.09s，超調量約為7.8%；x方向模糊PID響應時間為0.035s，超調量為6.8%，當在0.2s后施加0.1mm的位移信號時，再次恢復穩定的調節時間為0.1s，超調量約為6.5%；設置θ方向參考弧度為10mrad，模糊PID控制的響應時間為0.043s，超調量約為8.7%。當在0.2s后施加5mrad的弧度信號時，再次恢復穩定的調節時間為0.12s，超調量約為8.9%。結果表明，模糊PID控制下的多自由度磁懸浮驅動器動子可以維持動態穩定，在受到干擾之后也能迅速恢復穩定狀態。

綜合仿真結果可知，磁懸浮驅動器的兩種位移控制系統均具備較高的控制精度和較快的響應速度以及較優的跟隨效果，采用磁懸浮驅動器結合該控制系統來代替傳統電火花加工采用的電機加滾珠絲杠的驅動方式，可以快速調節異常的極間電壓，增加加工過程中的有效放電概率，從而提高加工效率。

3.3 多自由度磁懸浮驅動器實驗分析

多自由度磁懸浮驅動器位移實驗平臺如圖13所示。實驗設備主要包括計算機、dSPACE、直流開關電源、功率放大器、位移傳感器、多自由度磁懸浮驅動器。通過端口連接dSPACE實現端口數字信號與模擬信號轉換。將高精度位移傳感器檢測到的位移和位移變化量作為該控制系統的輸入變量，經過控制器產生電壓信號，經過功率放大器轉換為電流信號輸出到該磁懸浮驅動器的空心線圈中。

在MATLAB中搭建多自由度磁懸浮驅動器控制框圖，對反饋位移進行檢測，測試在幾個自由度方向上的響應速度以及施加階躍信號后的調節情況。比例系數、積分系數、微分系數需要依據實驗時發生的曲線波動進行實時調節。經過調節后z方向kp=9300，ki=10000，kd=65；x方向kp=8600，ki=9600，kd=55；θ方向kp=660，ki=1200，kd=1.3。在控制系統中分別對幾個自由度施加0.2mm、0.2mm、10mrad的階躍信號，觀察在期望位移變化后，該驅動器動子位移響應是否滿足電火花電極與工件間隙快速響應并調節的要求，實驗結果如圖14-16所示。

由階躍實驗結果可知，在傳統PID控制系統下，系統恢復z方向動子穩定的調節時間需要0.103s，響應時間為0.028s，超調量為51.5%；模糊PID控制下，系統恢復z方向動子穩定系統調節時間為0.085s，響應時間為0.016s，超調量為38.5%。兩者相比，模糊PID控制系統的調節時間較短，響應更快，超調量也較小；x方向PID控制條件下動子穩定的調節時間需要1.2s，響應時間為0.031s，超調量為36.5%。模糊PID控制下，x方向受到干擾的調節時間為0.53s，響應時間為0.023s，超調量為38.5%；θ方向在常規PID控制下，系統恢復θ方向動子穩定的調節時間為0.5s，響應時間為0.21s，超調量為22.0%。模糊PID控制下，系統恢復θ方向動子穩定的調節時間為0.25s，響應時間為0.13s，超調量為7.3%。兩者相比，模糊PID控制系統的響應更快，超調量較小。微細電火花要求極間間隙能夠在異常放電時進行快速調整，顯然模糊PID控制更符合要求。同時，本文增加正弦實驗來驗證控制系統響應特性，磁懸浮驅動器正弦跟隨實驗如圖17-19所示。

分別對幾個自由度進行正弦跟隨控制實驗可知，傳統PID控制系統和模糊PID控制系統正弦信號均能正常跟隨，平動定位行程為0.8mm，轉動定位行程為40mrad，可用于電火花極間間隙的快速響應，相比于傳統PID控制系統，模糊PID控制的跟隨效果較好。

4 結束語

本文提出了一種替代傳統電火花機床主軸運動的多自由度磁懸浮驅動器結構并對其工作原理進行了闡述。建立了多自由度磁懸浮驅動器動力學模型，基于此模型搭建了控制系統。通過有限元仿真軟件，對該磁懸浮驅動器內部空心線圈產生電磁力大小進行了仿真分析。通過設計兩種控制方法對磁懸浮驅動器進行了控制系統的仿真研究，通過階躍與正弦實驗驗證該磁懸浮驅動器的控制效果。實驗結果表明，該多自由度磁懸浮驅動器在不同自由度方向上均有良好的跟隨性能與響應速度。當電火花加工極間電壓出現異常時，磁懸浮驅動器可以滿足極間間隙的快速調整，進而提高電火花加工效率。

（責任編輯：鐘媛 英文審校：尹淑英）