“橡皮筋上的球”運動規律的研究
劉旭 趙泉翔 王振宇 劉偉
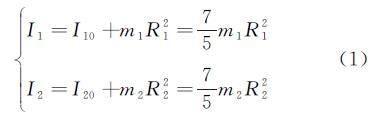

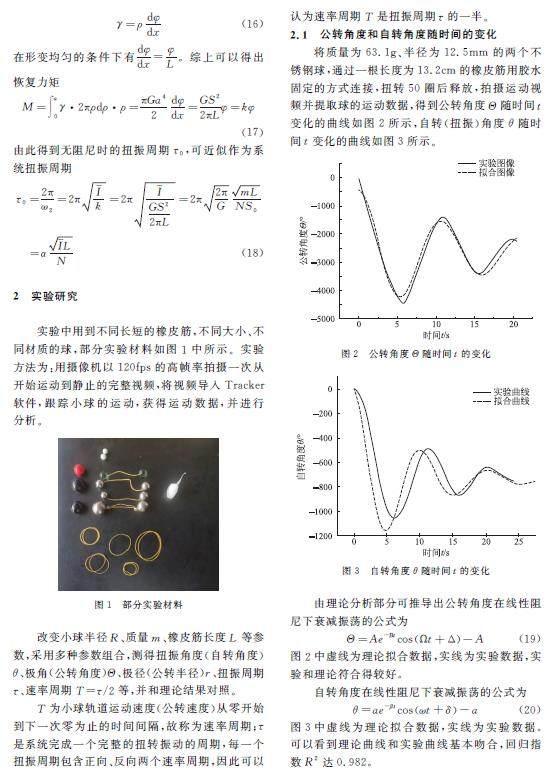
摘 要 本文對2022年IYPT 的一道題目“橡皮筋上的球”進行了研究,在對橡皮筋扭轉力和阻尼作線性假設的條件下,建立了二自由度線性阻尼自由扭振模型描述雙球橡皮筋運動規律,建立了彈性圓軸的剪切形變力學模型描述橡皮筋的力學性質,并給出解析解。本文解釋了雙球橡皮筋系統的“鐘擺”行為,定量探究了此行為與相關參數的依賴關系;通過Tracker軟件得到了相關實驗數據,驗證了模型的正確性,并對實驗中的等時性破缺現象進行了半定量解釋,對非線性公轉半徑r 隨時間t 的變化進行了定性分析。
關鍵詞 橡皮筋;球;線性扭振;剪切形變;振動
2022年IYPT 有一道題目是有關“橡皮筋上的球”運動現象的研究:“Connect two metal ball with an elastic band, then twist the elastic bandand put the balls on a table. The balls will begin to spin in one direction, then in the other. Explainthis phenomenon and investigate how thebehaviour of such a “pendulum” depends on therelevant parameters.”
分析題目發現,我們需要一根彈力帶將兩個硬質球連接起來提供扭轉恢復力矩。常見的彈力帶一般有織物彈力帶、橡膠彈力帶(又稱橡皮筋)兩類,此外也可使用金屬材料的扭轉彈簧(又稱扭簧)提供扭轉恢復力矩。考慮到織物彈力帶由于其紡織工藝存在經緯向的差別帶來的各向異性,其雖具有出色的縱向伸縮彈性,但是其橫向剪切彈性卻并不好;并且考慮到實驗可行性,硬質球直徑在10mm 量級,因此彈力帶的長度和直徑分別在10cm、1mm 量級,長徑比約100∶1量級,這也是金屬扭簧難以實現的。綜上,可以完美符合實驗要求的橡皮筋變成了實驗的首選。
為了解題目,進行如下預實驗:(1)用502膠水將單根橡皮筋與兩個金屬球連接;(2)手持球,扭轉橡皮筋約幾十圈,然后在橡膠墊上釋放。觀察到系統做周期性的扭轉振動,兩球會先向一個方向公轉數周,再向相反的方向公轉數周,如此反復幾次直至系統能量耗盡,即雙球橡皮筋系統呈現出“鐘擺”振蕩行為:小球的自轉角度、公轉角度、公轉半徑、公轉線速度均呈現準期性的特征。
前人的研究主要針對橡皮筋拉伸與彈出建立的動力學數學模型[1],球在振動彈性膜上反彈的動力學模型[2]或者以扭曲實現扭轉制冷的能量分析方法[3]。本文通過構建理論動力學模型分析“橡皮筋上的球”,將橡皮筋與球視為一個系統整體分析,從理論力學力矩分析的角度將線性部分的模型進行定量計算,對“橡皮筋上的球”全新模型進行建模。
本文建立二自由度線性阻尼自由扭振模型描述雙球橡皮筋系統的運動,建立彈性圓軸的剪切形變力學模型描述橡皮筋的力學性質,給出了系統的扭振周期的表達式。在實驗中調整小球質量、半徑、橡皮筋長度、并聯橡皮筋條數等參數,并測量其扭振周期,對影響系統周期性的參數進行定量分析,反推出了橡皮筋的剪切模量,從多方面驗證了理論的合理性。此外還發現雙球橡皮筋系統運動周期的非等時性,認為非線性系統阻尼和橡皮筋的多階盤繞是導致周期等時性破缺的兩個主要因素,并做了相應的半定量分析。本文還對公轉半徑r 隨時間t 近似呈振蕩衰減的關系以及系統能量耗散的來源進行了定性分析。
該實驗雖然裝置簡單,但現象引人入勝,實際上雙球橡皮筋系統的“鐘擺”振蕩行為中蘊含著極為豐富的力學知識,對該問題的研究不僅有助于同學們更深刻地理解理論力學,尤其是振動相關的知識,并且該問題所蘊含的非線性等內容更是當今控制科學與自動化領域的基礎問題,對該問題的研究將增進人們對該領域的理解,也可以極大激發同學的學習和研究興趣。
1 理論分析
設兩球為質量均勻的球體,質量分別為m1,m2,半徑分別為R1、R2,繞質心的轉動慣量分別為I10、I20,繞地面接觸點的轉動慣量分別為I1、I2,則有
為反映雙球橡皮筋系統的“鐘擺”振蕩行為的主要特征,作以下簡化假設:
(1) 主要關注小球的自轉公轉情況,不考慮徑向運動的情況,忽略橡皮筋長度這一自由度的變化,令兩小球繞橡皮筋分別轉過的角度θ1、θ2為系統的廣義坐標。
(2) 橡皮筋粘性阻尼線性假設:將橡皮筋在整個運動過程中的本構關系近似為線彈性,記橡皮筋扭轉剛度系數為k,將小球所受橡皮筋的阻力矩近似為正比于小球繞橡皮筋轉動角速度的粘性阻尼,記橡皮筋阻力矩的粘性阻尼系數為c。
(3) 滾動阻尼線性假設:假設小球受到的除橡皮筋阻力矩以外的滾動阻力矩正比于小球繞質心轉動慣量I10 、I20(也因此正比于繞地面接觸點的轉動慣量I1、I2)和小球繞橡皮筋轉動的角速度?θ1、?θ2 的乘積,故記其大小為σI1?θ1、σI2?θ2,其中σ為比例系數。
基于以上假設,由相關理論力學知識,下面建立雙球橡皮筋系統“鐘擺”振蕩行為的粘性線性阻尼扭振模型[4-7]。
雙球橡皮筋系統在線性阻尼作用下做二自由度的自由扭振,得到系統的扭振動力學方程為
次要誤差主要為系統誤差,且可以通過特定的方式縮小影響,主要有以下兩點。
(1) 打滑與彈跳的影響。質量和半徑都較大的球轉動慣量大,滾動摩擦力矩大,啟動困難,在經歷第一個振蕩周期后,難以自發進行后續的振蕩周期,導致周期性參量測量誤差較大;質量小的球 (r<10mm),與平面接觸的正壓力小,最大靜摩擦力小,導致橡皮筋最大扭矩超過了不打滑的閾值,使得系統在扭振過程中,出現嚴重的球打滑或者彈跳現象,造成不必要的能量衰減,帶來誤差。選擇質量適中、密度較大的鋼球在橡膠墊上進行實驗可以有效減少打滑和彈跳,使其對實驗影響幾乎忽略不計。
(2) 用502膠水連接橡皮筋與球時,會使橡皮筋與小球接觸的一小段硬化,導致實驗與模型出現偏差,影響較小。
4 結語
本文針對雙球橡皮筋系統,創新性構建了二自由度的線性阻尼自由振動模型和彈性剪切形變模型,對“鐘擺”行為與橡皮筋橫截面積、小球質量及半徑的關系等進行了實驗研究。實驗數據表明理論模型與實驗結果擬合良好,解釋了系統的運動規律,并對系統周期的非等時性進行了分析。本實驗材料獲取容易,操作簡單方便,但是實驗現象卻直觀有趣,并蘊含了豐富的力學知識,可用于大學物理實驗教學的研究型項目拓展。
參考文獻
[1] LI X, SUN B, ZHANG Y, et al. Dynamics of rubber bandstretch ejection[Preprints]. 2021, 2021030294. https://doi.org/10.20944/preprints202103.0294.v1
[2] EICHWALD B, ARGENTINA M, NOBLIN X, et al. Dynamicsof a ball bouncing on a vibrated elastic membrane[J]. Physical review. E, Statistical, nonlinear, and softmatter physics, 2010, 82(1 Pt 2):016203-016203.
[3] WANG R, FANG S, XIAO Y, et al. Torsional refrigerationby twisted, coiled, and supercoiled fibers[J]. Science,2019: 216-221.
[4] 周衍柏. 理論力學教程[M]. 3版.北京:高等教育出版社,2009:224-229.
[5] RAO S S. 機械振動[M]. 4版. 李欣業,張明路,譯. 北京:清華大學出版社, 2009:94-96.[6] 劉延柱, 陳立群, 陳文良. 振動力學[M]. 3版.北京:高等教育出版社, 2019:147-149.
[7] 陳予恕. 非線性振動[M]. 1 版.北京:高等教育出版社,2002:30-35.
[8] 劉鴻文. 簡明材料力學[M]. 3版.北京:高等教育出版社,2016:65-68.
[9] 王進文. 硫化體系對天然橡膠低溫動態剪切模量的影響[J]. 世界橡膠工業,2004,31(12):30-36.
WANG J W. Effects of vulcanization system on dynamicshear modulus of natural rubber at low temperature[J].World Rubber Industry, 2004, 31(12): 30-36. (in Chinese)

