一種移動作業機器人環境交互作用模型分析

丁曉軍 馬 琴

（1.北方民族大學電氣信息工程學院，寧夏 銀川 750021；2.北方民族大學土木工程學院，寧夏 銀川 750021）

由于勞動力短缺和人口紅利逐漸消失，因此“機器人換人戰略”迫在眉睫，移動作業機器人正是在這個背景下應運而生[1]。根據機器人與環境交互的特性，可將其分為2類。一類是機器人在自由空間中的非接觸（無約束）運動，沒有相關的環境影響施加在機器人上，例如抓取-放置、噴涂和電弧焊等簡單任務[2]；另一類是一些復雜的高級任務，例如裝配和加工，需要考慮機械手與環境之間的耦合[3]。

本文分析了移動作業機器人與環境交互作用過程，并基于拉格朗日方程推導了接近、受限運動和沖擊3種情況下機器人-環境交互作用模型。然后，仿真驗證由4個麥克納姆（Mecanum）輪構成的全向移動平臺和由1個6自由度操作臂組成的移動作業機器人。

1 臂-環境交互作用模型

在機器人操作臂末端安裝執行器，在進行作業的過程中，機器人將與環境接觸。一般將接觸任務劃分為3個階段，即接近、沖擊和受限運動。在接近階段，末端執行器向約束移動，以低速接近目標物，以避免碰撞。但是，在實際工況中，機器人會受到擾動影響，進而與約束發生碰撞，導致速度發生突變，沖擊階段結束后，開始受限運動階段。為了便于描述，本文先分析接近（自由）階段和受限運動階段2個運動過程，然后分析沖擊階段。

1.1 接近階段

操作臂與環境交互如圖1所示。接近階段如圖1（a）所示，r為操作臂，e為動態環境。假設操作臂有nr個自由度，環境有ne個自由度，采用位置向量分別定義操作臂與環境的運動，則整個系統的位置可用一個統一的向量q表示，如公式（1）～公式（3）所示。

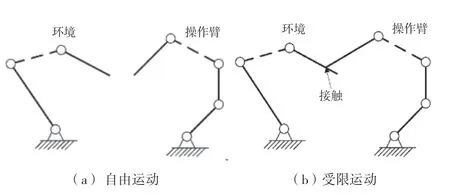
圖1 操作臂與環境交互

式中：q的維數為n=ne+nr。

這2條鏈的動力學模型分別如公式（2）、公式（3）所示。

式中：,為速度；，為加速度；τe和τr為關節轉矩矢量；He和Hr為慣性矩陣；he和hr為重力、科里奧利力（Coriolis force）以及其他與位置和速度相關的力。

1.2 受限運動階段

受限運動階段如圖1（b）所示。為便于描述，2個鏈分別引入1組新的坐標（外部坐標）se和sr，令se=（se1，...，sen），sr=（sr1，...，srn）。坐標q與坐標s之間的關系表征了運動學模型。將坐標se定義為絕對坐標，通常集合se與qe一一對應，并呈非線性關系，如公式（4）所示。

操作臂末端相對環境即固定在鏈條（e）最后一環的坐標的坐標變換如公式（5）所示。

則整個系統的外部坐標如公式（6）所示。

外部坐標sr是為了便于描述給定的任務而定義的，當發生接觸時，這些坐標中的一些值將減為0，當1個接觸約束限制了nc個自由度時，nc坐標從集合sr減至sr-nc。f為自由坐標，將sf定義為整個系統自由坐標的集合，c為受接觸約束，sc為包括受接觸約束的坐標的集合，因此sf的維數為ne+nr-nc=n-nc，sc的維數為nc，如公式（7）所示。

約束（接觸）如公式（8）所示。

從動力學的角度進行分析，由于接觸產生反作用力，因此力分量的數目等于受限制的自由度的數目，在這種情況下的動力學模型如公式（9）、公式（10）所示。

式中：為操作臂與環境接觸后受約束環境的雅可比矩陣；為操作臂與環境接觸后受約束操作臂的雅可比矩陣。在公式（8）的約束條件下，公式（9）、公式（10）中的坐標qe和qr并不是獨立的。因此，公式（8）、公式（9）以及公式（10）構成了整個系統的動力學模型，并表示ne+nr+nc個標量方程的集合，通過求解可得運動（qe，qr）和接觸力F。為了得到適合數值積分的形式，對公式（8）進行求導，得到其約束的微分形式。

sc的一階導數如公式（11）所示。

式中：為sc的一階導數，為系統的速度。

sc的二階導數如公式（12）所示。

式中：為sc的二階導數，為系統的加速度；雅可比矩陣、與公式（9）、公式（10）中的相同，向量Ac如公式（13）所示。

公式（8）的微分形式如公式（14）所示。

公式（9）、公式（10）和公式（14）構成了整個系統的動力學模型。該模型包括ne+nr+nc個標量的線性方程，可以求解相同數量的未知數，包括ne維加速度分量，nr維加速度分量和nc維接觸力F。

考慮摩擦因素，將集合sf分離為sf=（se，），包括nr-nc個坐標，摩擦力的方向與接觸點的相對速度方向相反，如公式（15）所示。

式中：Ff為nr-nc個分量的摩擦矢量；|Ff|為其絕對值；v0為nr-nc個分量的矢量，它定義了相對速度的方向，其大小取決于接觸力、表面質量和相對速度。選取|Ff|=μ|F|，其中，摩擦系數μ是常數。然而，精確的模型需要考慮相對速度矢量v0對μ的影響。矢量v0的方向由相對速度srf決定，如公式（16）所示。

式中：為操作臂與環境接觸后未受約束操作臂的雅可比矩陣；為操作臂與環境接觸后未受環境約束的雅可比矩陣。因此，v0與位置向量qe、qr和速度、均相關，摩擦力Ff如公式（17）所示。

公式（17）的具體形式視情況而定。

當接觸點有相對速度時，摩擦系數μ從零速度下的靜態摩擦變為動態摩擦，隨著接觸點相對速度增大，當摩擦系數克服發生運動的摩擦臨界值時，摩擦系數由負黏性摩擦變為黏性摩擦。摩擦力的存在會影響系統的動力學特性，因此，考慮摩擦后，公式（9）、公式（10）變為公式（18）、公式（19）。

當接觸物體間存在相對運動時，公式（14）、公式（18）和公式（19）構成了整個系統的動力學模型。雖然公式（17）中未知數的數量沒有增加，但是需要求解、和F。

假設在某一時刻相對運動完全停止（=0），那么公式（15）和公式（17）將不再適用，公式（18）、公式（19）中的摩擦力Ff變得不可解，這時需要增加一個條件，從相對運動不存在這一事實出發，如公式（20）所示。

公式（14）、公式（18）、公式（19）與公式（20）構成了系統的動力學模型，通過該模型，可以求解加速度、和反作用力F、Ff。將模型計算的Ff值與系統靜摩擦值進行比較，當其值大于靜摩擦值時，會再次產生相對運動，求解過程切換回公式（14）、公式（14）、公式（17）、公式（18）以及公式（19）。

1.3 沖擊階段

沖擊是接觸任務的第二個階段。面約束下的沖擊是最常見的，因此本文主要分析面約束下的沖擊問題。此時，sc（即坐標s6）變為0并且沖擊作用會沿著這個方向進行。如果考慮約束面的彈性，則可能出現跳躍。為了便于推導，這里僅考慮非彈性范圍內的沖擊問題。基于這種假設，操作臂末端執行器不會在第一次接觸后離開表面，而是沿著表面移動。

如果碰撞面是2個，則sc的維數是2，以此類推，當有nc個碰撞面作用時，sc的維數是nc。復雜的沖擊會導致表面發生一系列碰撞，為了方便分析，在接下來的交互分析中忽略這種影響。

求解沖擊動力學問題。在沖擊區間上對約束運動模型進行積分，令t1為碰撞發生的時刻，t2為沖擊結束的時刻，則發生碰撞的時間間隔為Δt=[t1，t2]。對幾何約束和非彈性沖擊來說，可以認為這個區間很短，即當Δt→0，t2→t1，在此區間內對公式（10）進行積分，如公式（21）所示。

公式（21）、公式（22）描述了沖擊的動態過程。它們是6+nc個標量方程的集合，可以求解和FΔt，為六分量關節速度變化量；FΔt為nc個分量的沖量，當Δt→0時，FΔt≠0，即F→∞。在無限短的撞擊時間內，位置不會改變，即q1=q2。

基于碰撞過程發生的3個階段，采用數值方法求解具體碰撞任務的一般過程。在接近階段，對公式（3）進行積分，并檢驗sc的坐標值；當sc坐標值變為0時，轉向沖擊公式（21）、公式（22）并計算速度變化量。利用這個新的初始狀態，對公式（10）和公式（14）積分來求解約束運動的動力學方程。綜上所述，當sc為0時，接近階段結束，在那個瞬間碰撞時間間隔非常短，隨后開始較規律的受限運動。

2 仿真分析

建立由4個Mecanum輪構成的全向移動平臺和1個由六自由度操作臂組成的MMR仿真模型來驗證本文采用的交互作用分析方法的有效性。機器人的設計參數[4]見表1。對臂-環境的交互作用進行仿真，時間間隔設為t∈[0，2] s，地面傾斜角θm、側傾角γm設為0°。

表1 機器人的設計參數

本文以典型的有摩擦接觸任務-寫字任務來分析臂-環境交互作用。為了簡化計算，將小車固定，控制操作臂寫漢字“一”，如圖2所示。寫字任務從A位置開始，在接近階段由PD調節器控制機器人。

圖2 六自由度操作臂執行有摩擦的接觸任務

機器人從A到B的運動結果如圖3所示，即坐標x、y和z隨時間的變化以及其速度隨時間的變化。通過分析，得到如下結論，預期的非零速接觸是合理的，當參考軌跡沒有碰撞時，機器人末端到達表面的速度不為0，如圖3（e）所示。

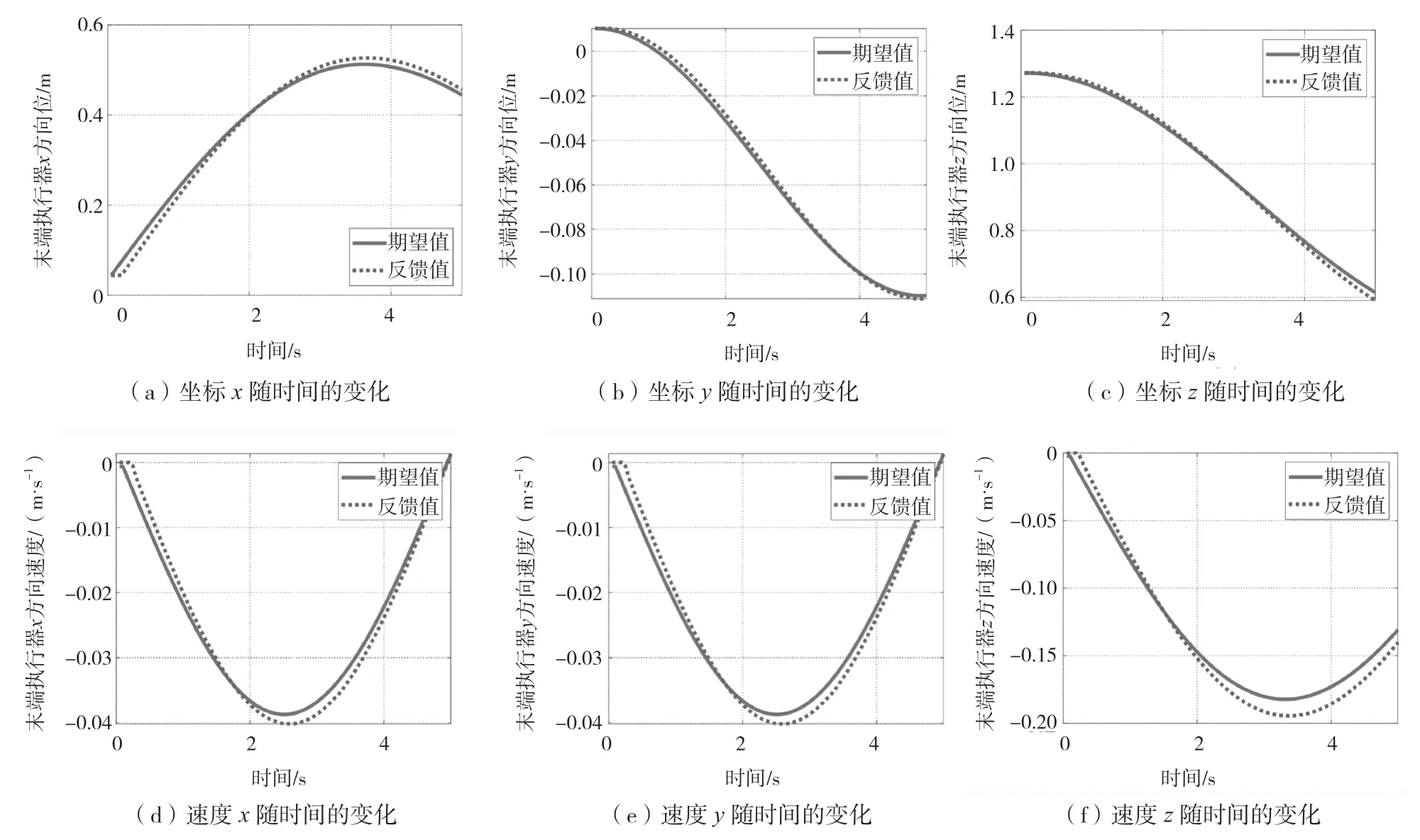
圖3 臂-環境交互：接近階段

沖擊階段各關節瞬時速度的變化曲線如圖4所示，沖擊時間為5 s。撞擊后會發生堵塞，速度降至0。

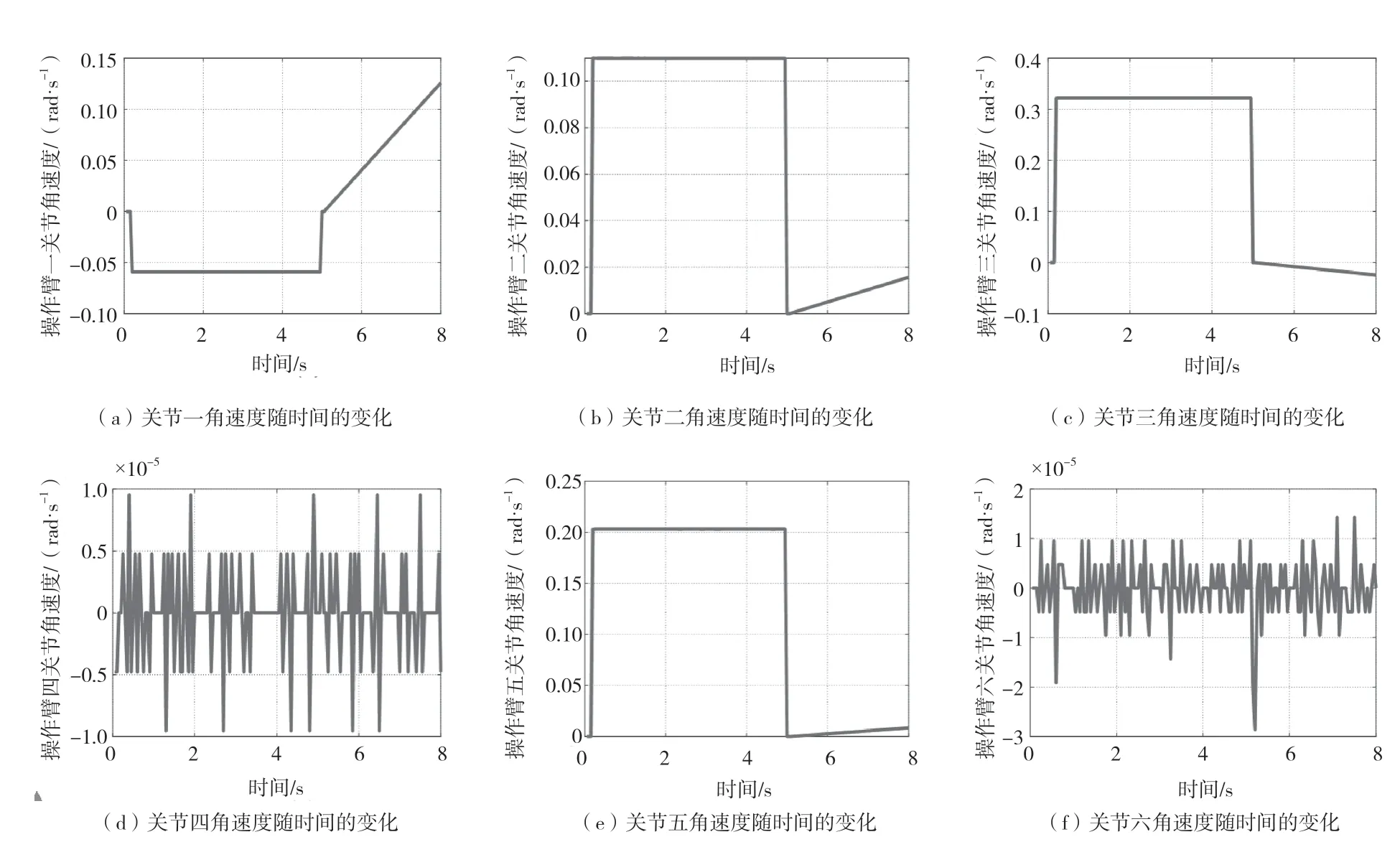
圖4 臂-環境交互：沖擊階段

采用經典的力/位混合控制實現約束運動。操作臂x向位置和速度曲線隨時間的變化如圖5所示。可能會看到機器人的尖端停止在C位置，但是不會立即開始往回移動，這是因為發生了“堵塞”（實則為接觸運動的黏著階段），所以堵塞周期約0.05 s。之后，機器人的末端運動指向B。

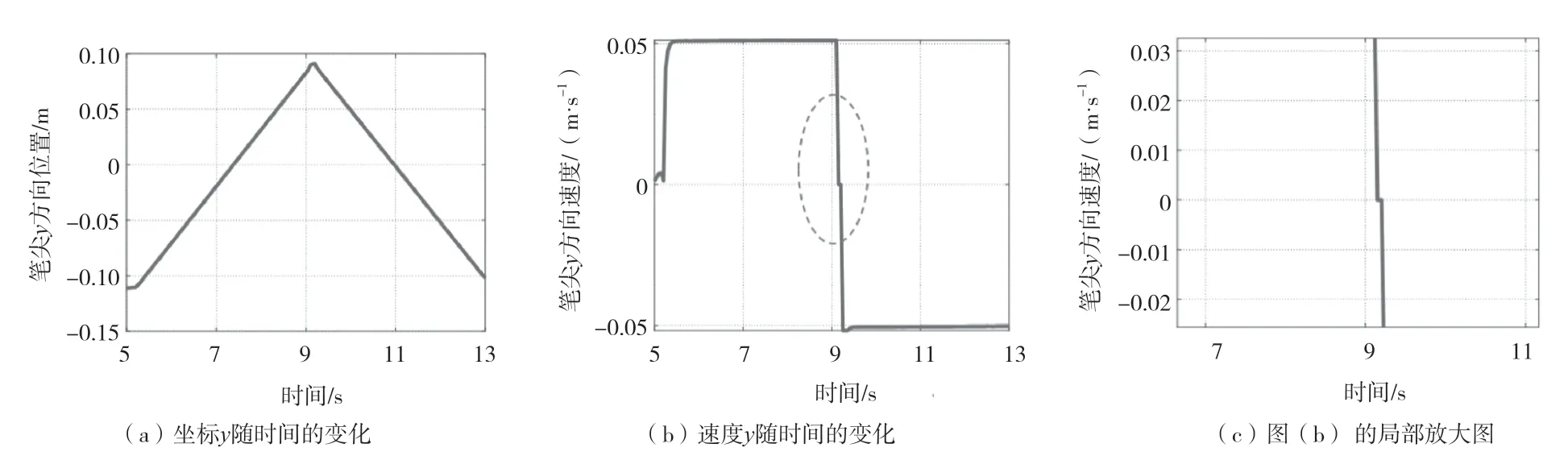
圖5 臂-環境交互：受限運動階段

反作用力F和摩擦力Ff的摩擦力方向在點C發生了變化，但是沒有立即變化，如圖6（c）所示。在阻塞過程中，摩擦力上升，當它達到μF值時，操作臂末端再次開始運動。反作用力F會有波動，這是因為實際機器人并不是純剛體。

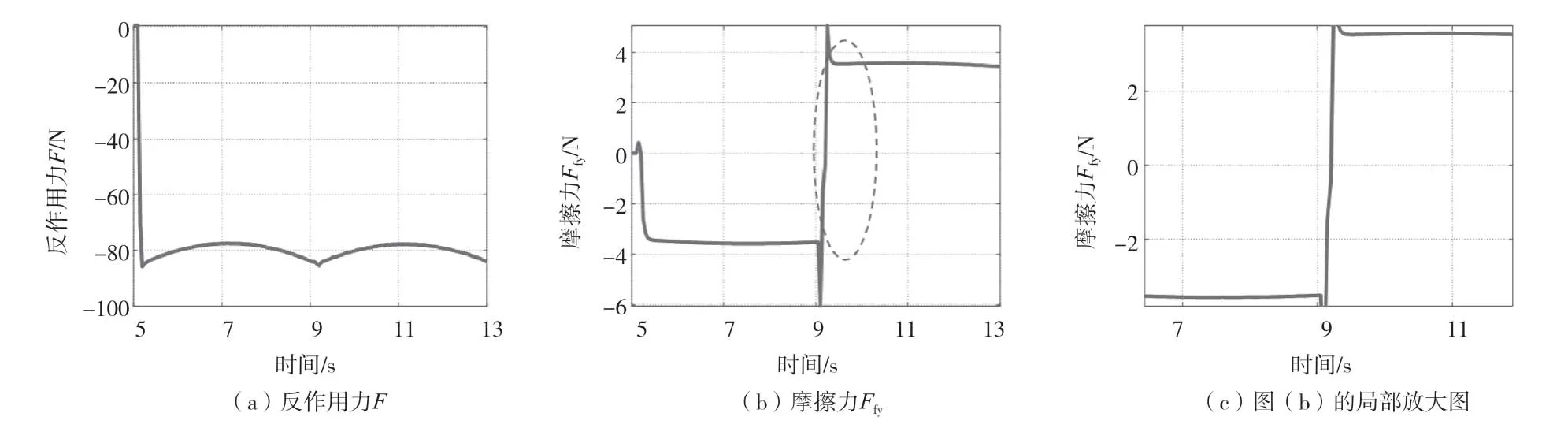
圖6 臂-環境交互：接觸點的力

3 結論

本文基于拉格朗日方程推導了在接近、沖擊和受限運動3個階段的機器人-環境交互作用模型，并對其進行了仿真分析。仿真結果驗證了交互作用模型的合理性和有效性，為建立完整的移動作業機器人動力學模型提供依據。