基于改進經驗模態分解的直線電機伺服系統迭代學習控制

劉思諾 武志濤

基于改進經驗模態分解的直線電機伺服系統迭代學習控制

劉思諾 武志濤

（遼寧科技大學電子與信息工程學院，遼寧 鞍山 114051）

針對直線電機伺服系統迭代學習過程中因誤差積累效應引起的收斂速度慢和跟蹤精度差的問題，提出一種基于改進經驗模態分解的控制策略。首先，設計一種具有自適應性調節特點的迭代學習位置控制器。然后，提出一種基于三角極值波延拓與互補集合經驗模態分解的改進算法，該算法可將各次迭代的跟蹤誤差進行分解，篩選并剔除影響誤差收斂的分量。通過仿真分析并與傳統迭代學習控制進行比較，證明了本文方法具有更快的收斂速度，能夠以較少的迭代次數實現直線電機的高精度跟蹤控制。

永磁直線同步電機（PMLSM）；迭代學習；改進經驗模態分解；收斂速度

0 引言

隨著高速高精密加工技術的快速發展，永磁直線同步電機（permanent magnet linear synchronous motor, PMLSM）展現出取代傳統運動執行器（如旋轉式電機加螺桿或傳導絲杠）的趨勢[1]。PMLSM以其高速度、高精度和強推力等優點，在工業機器人、運送傳輸設備和磁懸浮列車等領域得到廣泛應用。然而，由于PMLSM缺乏機械傳動環節，它無法緩沖內部參數變化及外部非線性擾動等因素的影響，這增加了伺服控制的難度[2]。

迭代學習控制（iterative learning control, ILC）利用之前迭代的數據，在連續重復任務中改善當前系統的控制輸入信號，從而抑制重復性干擾，并實現在有限范圍內的完全跟蹤[3-5]。然而，ILC的積分特性可能放大非重復性擾動，從而影響系統的魯棒性。文獻[6]提出一種基于擴張狀態觀測器的數據驅動ILC方法，它能有效抑制系統的隨機擾動，但未考慮時間滯后的影響。文獻[7]在PMLSM伺服系統中引入Smith預估器，以減少ILC過程中時間滯后效應的累積影響，但該方法的設計需要系統具有精確的過程模型。此外，文獻[8]提出一種無模型數據驅動的自適應ILC方法，避免了由于模型不準確而導致系統性能下降的問題，但該方法無法抑制非重復擾動。文獻[9]通過設計時域補償器來補償ILC過程中的干擾，提高系統對非重復擾動的魯棒性，但該方法未考慮誤差的累積影響。

由于系統動態特性的變化或外部擾動的存在，ILC可能導致誤差在每次迭代中逐漸累積，進而對PMLSM伺服系統的跟蹤精度產生不利影響。為了解決這一問題，本文提出一種基于改進經驗模態分解（modified empirical mode decomposition, MEMD）的迭代學習控制策略。首先，設計一種自適應比例微分（proportional differential, PD）型迭代學習位置控制器；然后，利用改進經驗模態分解算法對跟蹤誤差信號進行分解，剔除發散的誤差分量，并重新應用于迭代學習過程中；最后，通過仿真證明所提方法的有效性。

1 PMLSM數學模型

基于d=0的矢量控制，PMLSM在dq坐標系下的電壓方程為[10]

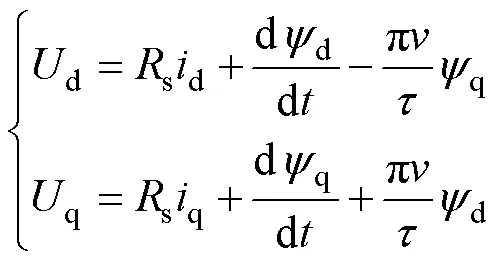
其中

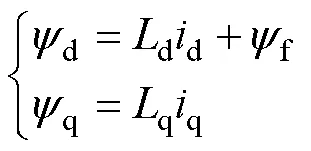
式中：d、q為d、q軸的電壓；d、q為d、q軸的電流；d、q為d、q軸的電感；s為動子相電阻；d、q為d、q軸的磁鏈；為動子線速度；為極距；f為永磁體磁鏈。

電磁推力e為

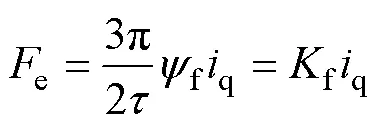
式中，f為推力系數。

PMLSM的機械運動方程為

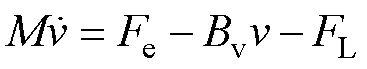
式中：為動子質量；v為摩擦阻力系數；L為負載、端部效應及參數失配引起的干擾。

結合式（3）和式（4），可得PMLSM的數學模型為

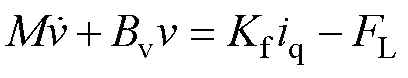
因此，PMLSM的傳遞函數為

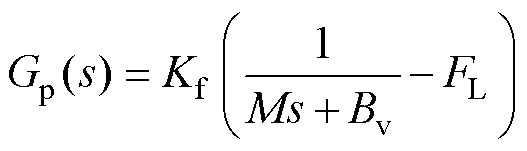
2 迭代學習位置控制

為了減少PMLSM在重復任務中的位置跟蹤誤差，本文采用ILC設計一個位置控制器。PMLSM自適應迭代學習控制系統框圖如圖1所示，其中表示PMLSM的速度閉環，v為比例積分（pro- portional integral, PI）控制器。

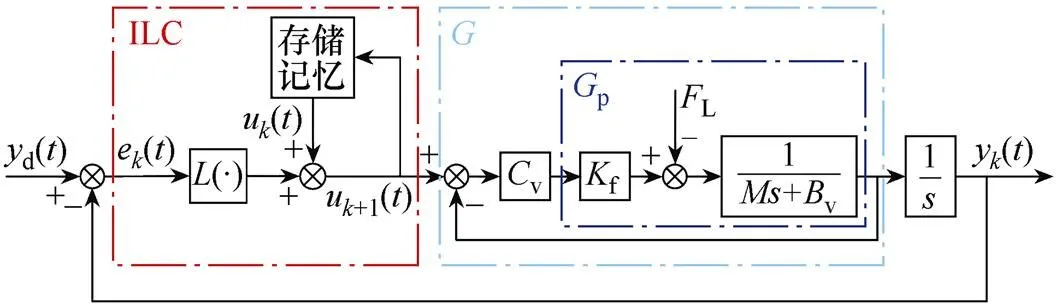
圖1 PMLSM自適應迭代學習控制系統框圖

由圖1可知

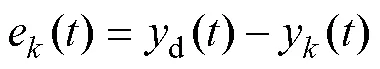
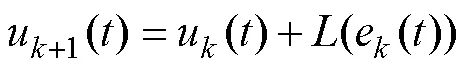
本文提出的自適應PD型學習律為

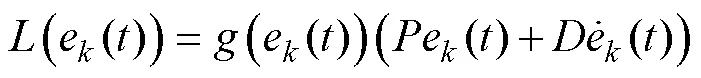
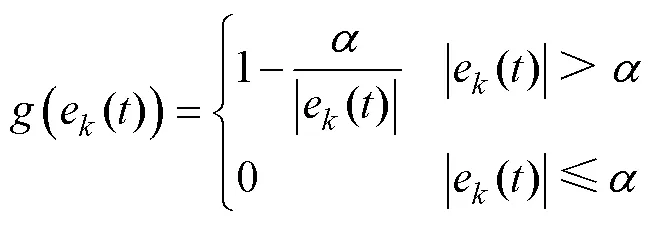
式中：、為學習增益系數；(×)為與誤差邊界相關的函數。

3 基于MEMD的迭代學習控制

為了減少誤差積累效應[11]的影響，提出一種基于MEMD的迭代學習控制策略，以提升系統的位置跟蹤性能。

3.1 MEMD算法

MEMD算法是一種用于信號分解的數據分析方法[12]，旨在將非線性或非平穩信號分解為一組本征模態函數（intrinsic mode function, IMF），每個IMF代表一個具有不同頻率和振幅的本征模態。本文提出基于三角極值波延拓與互補集合經驗模態分解的MEMD算法。

1）三角極值波延拓的端點效應改進算法

端點效應會導致信號的上下包絡線向兩端發散，且該效應可延伸至下次分解的過程中，使分解效果不斷變差[13]。為了抑制端點效應，本文利用三角極值波延拓法進行處理，其示意圖如圖2所示。

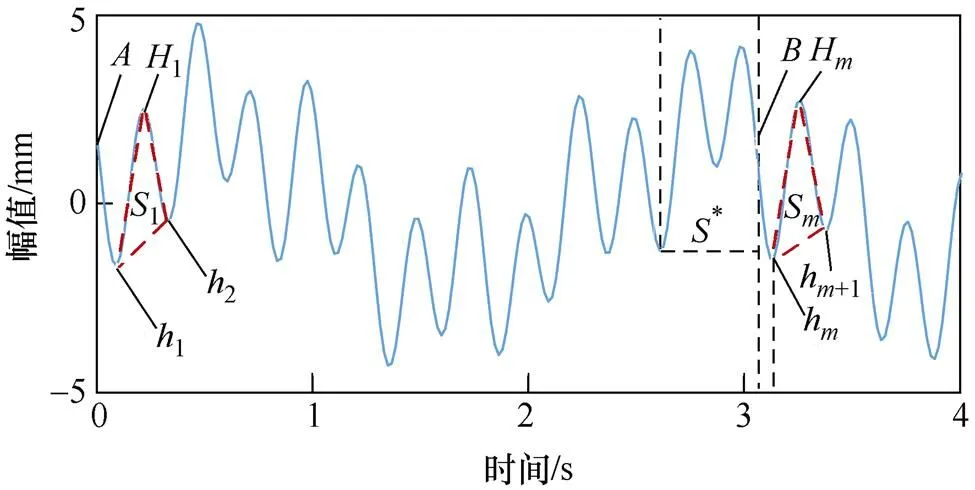
圖2 三角極值波延拓法示意圖

以數據左端點為例，波形延拓方法步驟如下：

（1）提取信號所有極值點。

（2）選取距離左端點最近的三個極值點構成的波形1作為模板子波，并將其余與模板子波1相似的極值波定義為匹配子波。

（3）利用模板子波1中三個極值點構成的三角形△112作為匹配對象，選取邊長、斜率、曲率作為特征量，計算匹配子波S中極值點所確定的三角形△hHh+1的匹配誤差，其值越小，匹配度越高。匹配誤差計算公式如下[14]。

邊長匹配誤差為

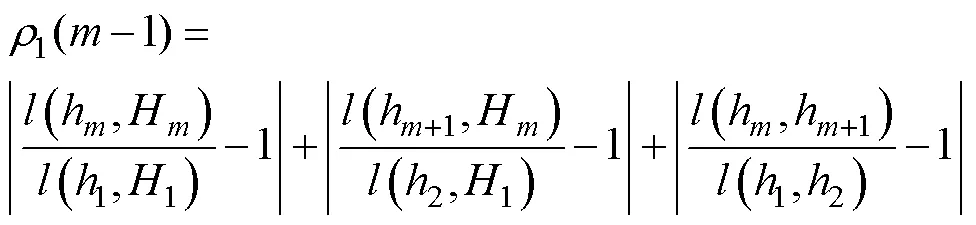
斜率匹配誤差為

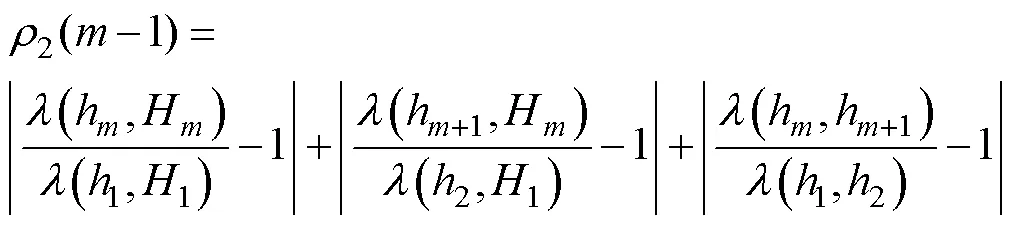
曲率匹配誤差為

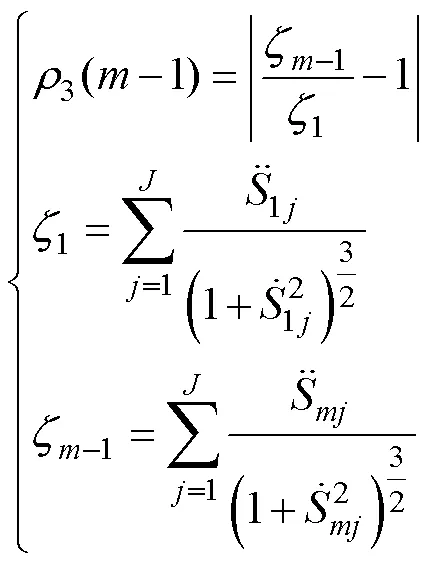
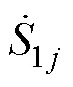
總體匹配誤差為

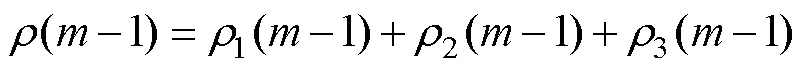
（4）波形延拓。設S為最佳匹配子波，確定延拓連接點，使端點處波形1與匹配子波左側曲線Bh相對應，如圖2所示，S即為左端延拓波形。

2）互補集合經驗模態分解的模態混疊改進算法

模態混疊問題可能會造成錯假的時頻分布，導致信號分解結果失真[15]。本文采用的互補集合經驗模態分解算法通過引入互補且獨立分布的白噪聲，使分解信號的極值點分布更趨勻稱，從而抑制模態混疊問題，其過程如下：

（1）給定集合平均次數與白噪聲的幅值。

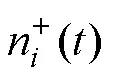
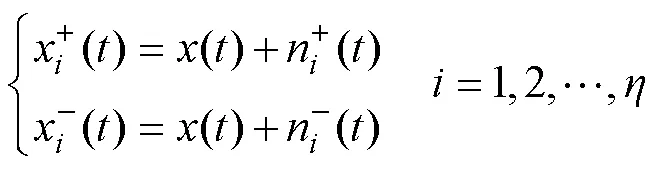
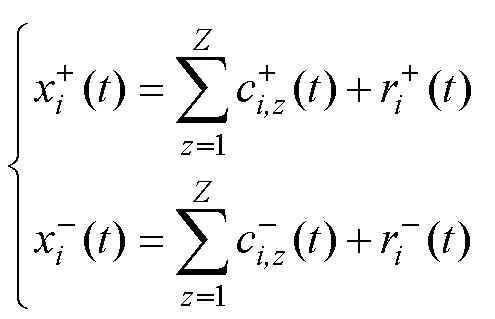
（4）重復上述步驟次，得到2組IMF分量。最后將2組IMF分量進行多次集成平均處理，得到最終的IMF分量，即

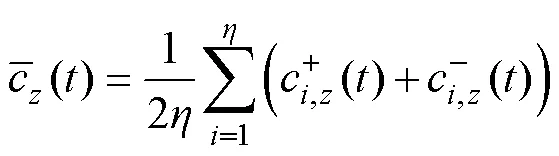
3.2 基于MEMD算法的迭代學習位置控制

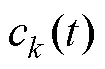
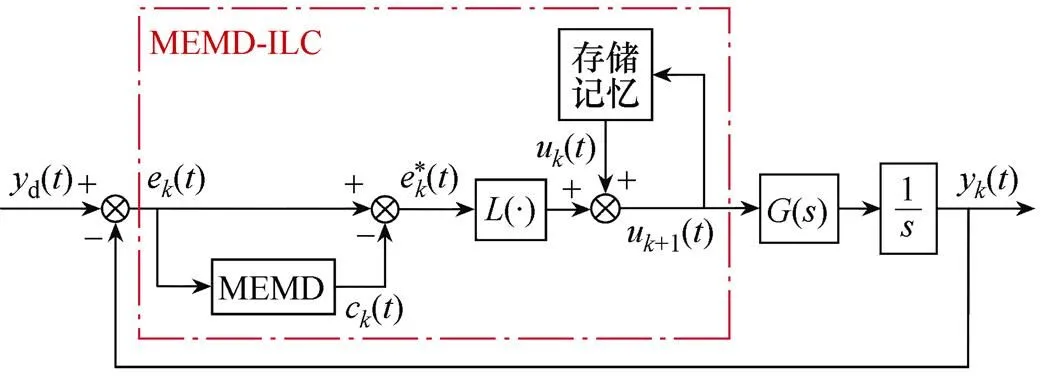
圖3 基于MEMD算法的PMLSM迭代學習控制系統框圖

基于MEMD算法的PMLSM迭代學習控制系統運行過程如下：

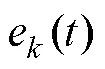
（4）利用重構的跟蹤誤差來計算控制輸入，并將該控制輸入應用于PMLSM迭代學習控制系統，可以實現更高效的學習。

4 仿真與分析

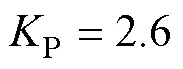
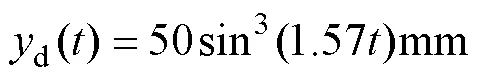
基于ILC方法的各次迭代跟蹤誤差的方均根（root mean square, RMS）見表1。根據表1可知，跟蹤誤差的方均根從未迭代的18.11mm減小到第10次迭代的4.73mm，減少了73.88%，但是其在第7、8次迭代時出現明顯增加。

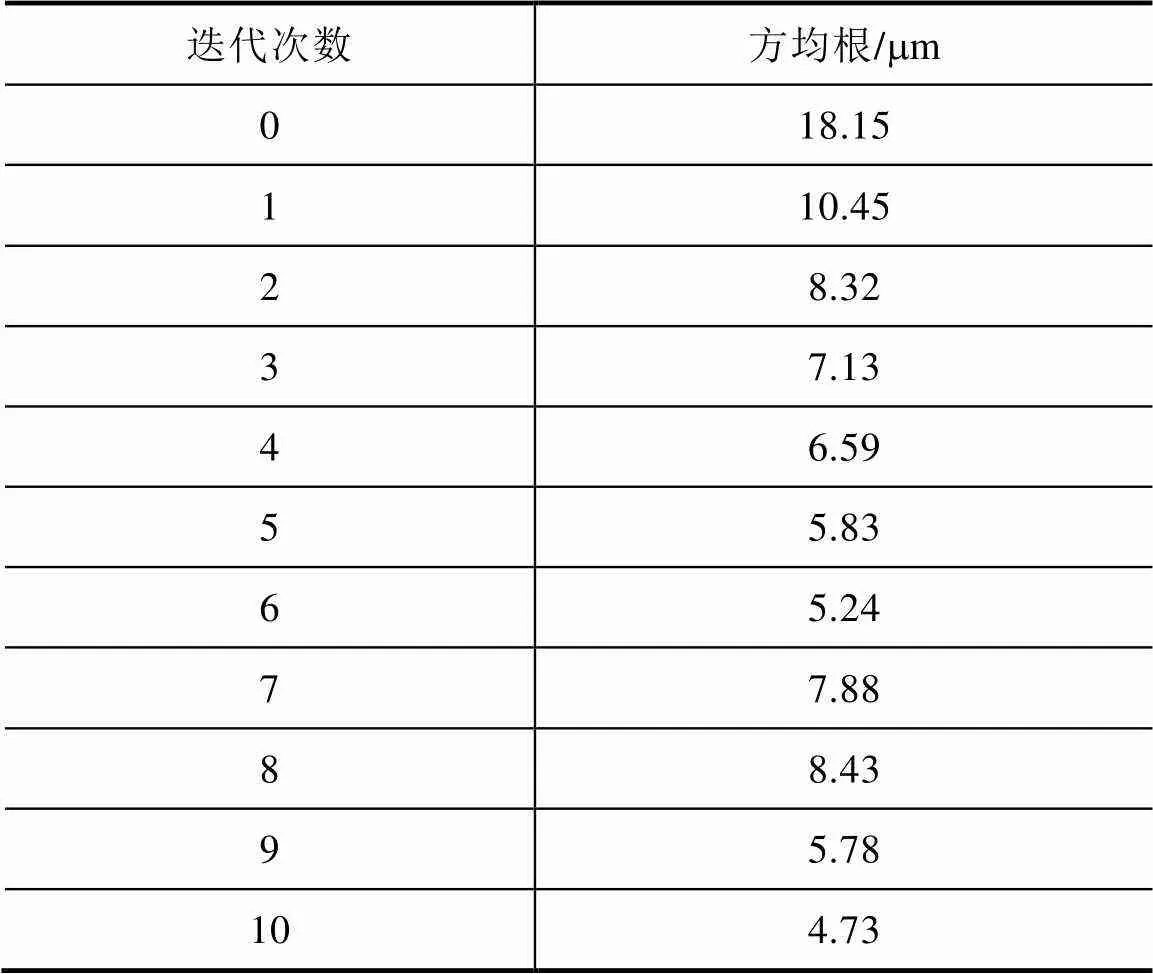
表1 基于ILC方法的跟蹤誤差方均根

圖4為采用ILC方法經過10次迭代后的位置誤差曲線，由圖可知，最大位置跟蹤誤差約為6.53mm。

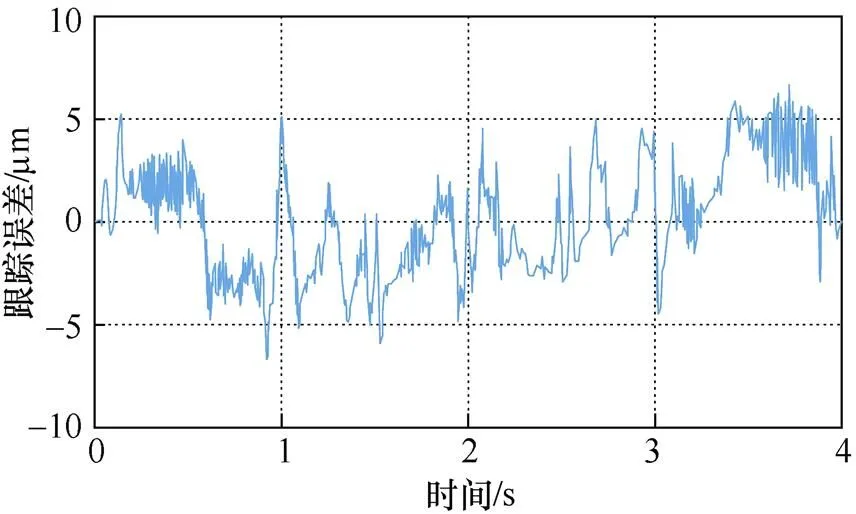
圖4 基于ILC方法的位置跟蹤誤差曲線

利用MEMD算法分解各次迭代的跟蹤誤差，得到的IMF分量如圖5所示。

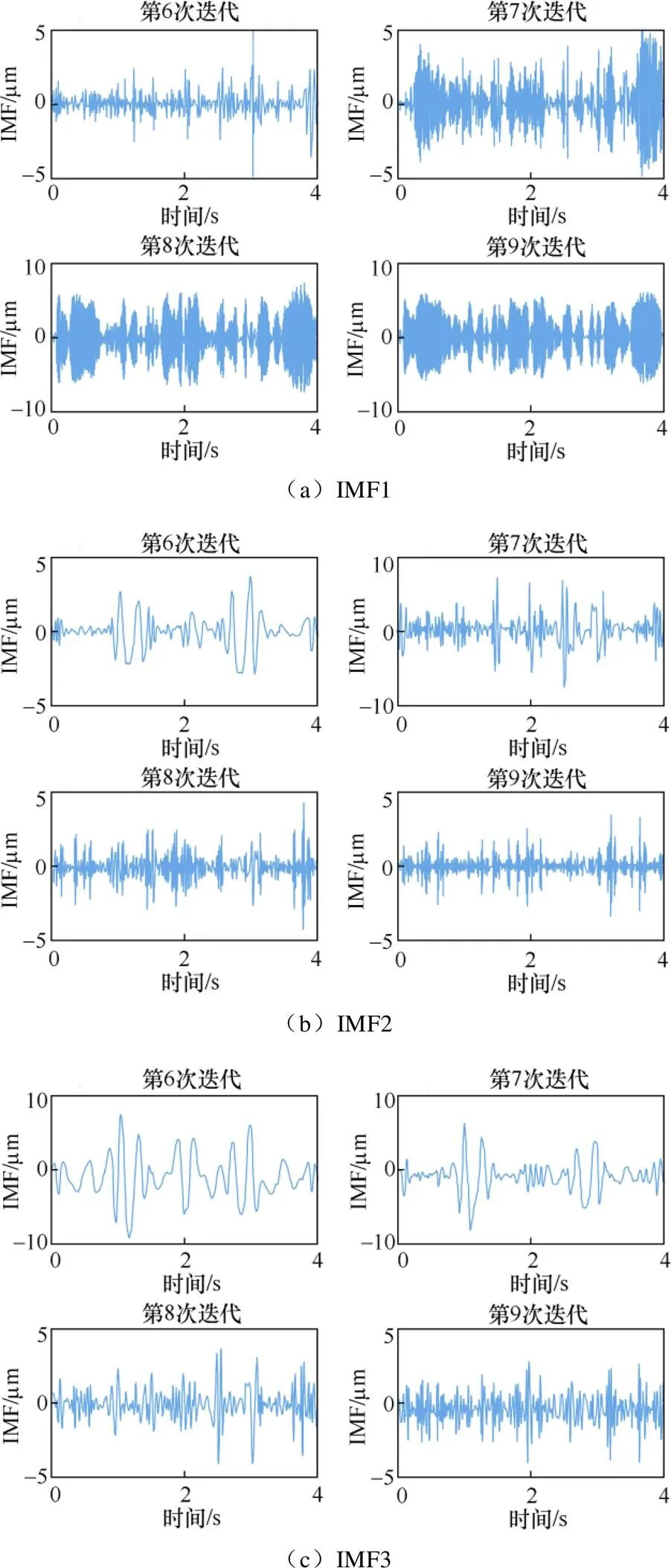
圖5 MEMD算法分解得到的IMF分量

從圖5（a）可以明顯觀察到，在第7次和第8次迭代時，IMF1的幅值出現了遞增現象。同樣地，圖5（b）顯示在第7次迭代時，IMF2的幅值有所增加。此外，在圖5（c）中，隨著迭代次數的增加，IMF3的幅值呈現單調遞減的趨勢。這表明主要是IMF1和IMF2分量影響了迭代學習過程的單調收斂，從而降低了系統的學習性能。因此，需要在第7次和第8次迭代時消除IMF1分量，并在第7次迭代時消除IMF2分量。將遞增的分量剔除后，重新運行系統，經過MEMD-ILC后系統跟蹤誤差的方均根見表2。

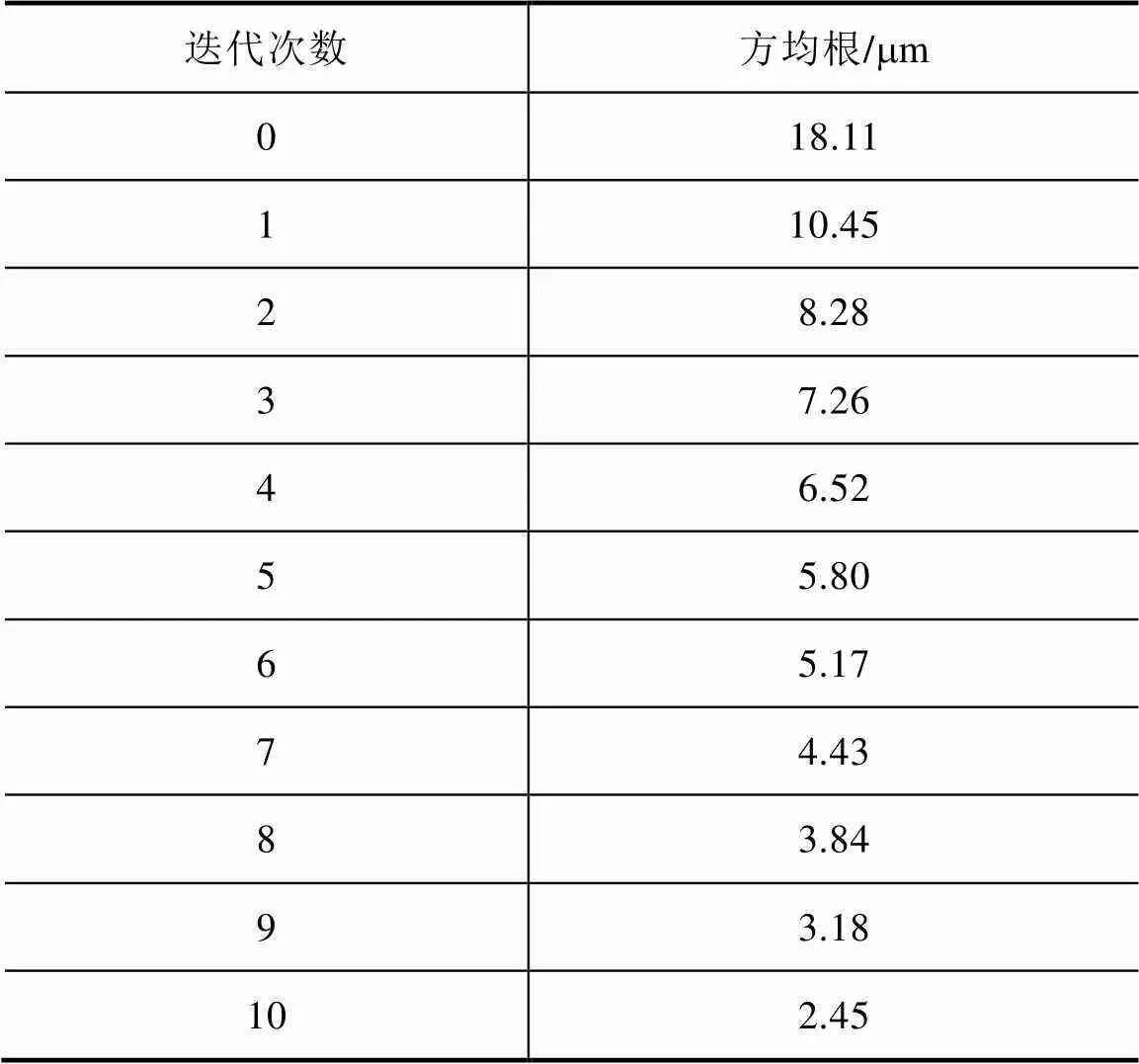
表2 基于MEMD-ILC方法的跟蹤誤差方均根

基于ILC和MEMD-ILC方法的跟蹤誤差方均根曲線如圖6所示。

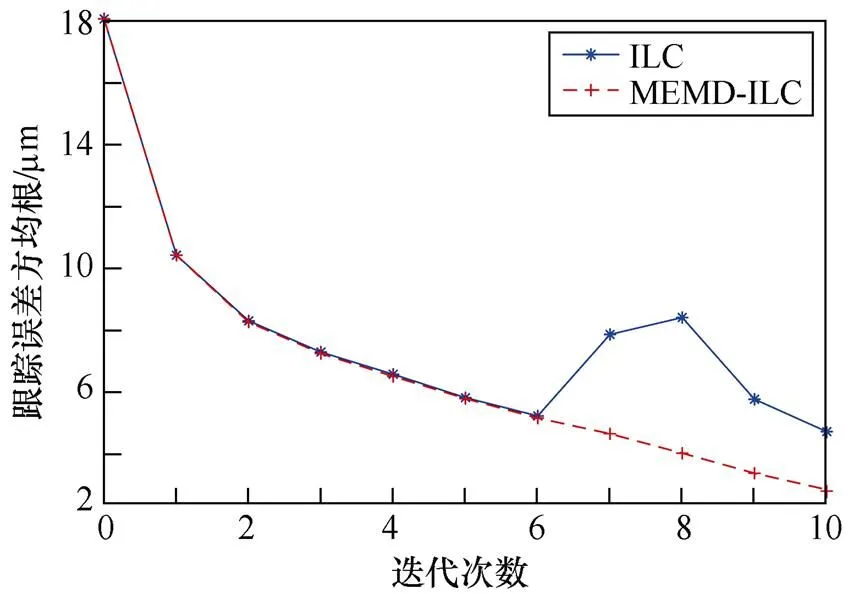
圖6 基于ILC與MEMD-ILC方法的跟蹤誤差方均根曲線

通過圖6可以觀察到，經過MEMD算法處理后，隨著迭代次數的增加，跟蹤誤差方均根從原來的不收斂變為單調遞減；在第10次迭代時，跟蹤誤差方均根降低至2.45mm，與僅使用ILC方法相比，減少了48.2%。因此，MEMD-ILC方法明顯改善了迭代效果。

基于MEMD-ILC方法的位置跟蹤誤差曲線如圖7所示。由圖7可知，基于MEMD-ILC方法的最大位置跟蹤誤差約為5.37mm，與圖4相比，最大跟蹤誤差減少了17.76%，這表明系統的位置跟蹤精度得到進一步提升。

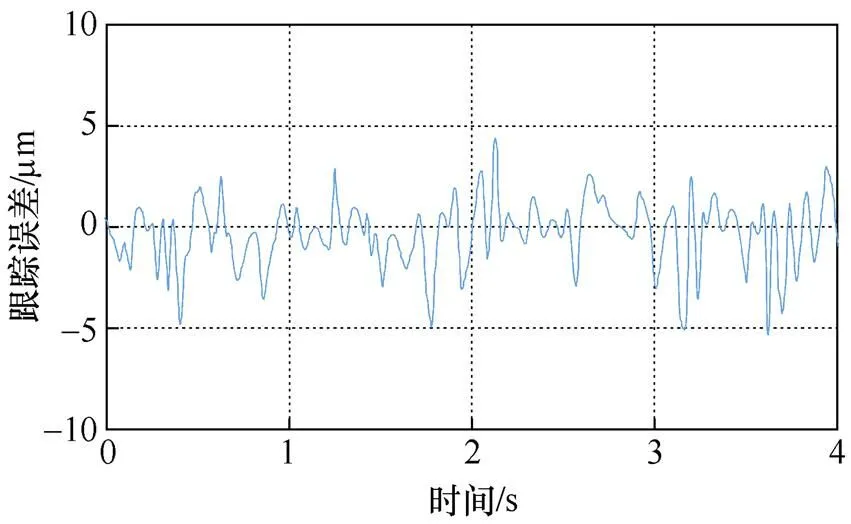
圖7 基于MEMD-ILC方法的位置跟蹤誤差曲線

5 結論

本文提出了一種基于MEMD算法的PMLSM迭代學習控制方法，旨在解決誤差積累效應導致的收斂速度慢和跟蹤性能差的問題。利用MEMD算法將各次迭代的跟蹤誤差進行分解，排除對系統收斂產生影響的誤差分量，并重新整合剩余的誤差分量，以提高迭代學習控制的收斂效果和跟蹤精度。仿真結果表明，相較于傳統的ILC方法，采用MEMD-ILC方法的位置跟蹤誤差減少了17.76%，PMLSM系統的位置跟蹤精度得到有效提升。

[1] 黃旭珍, 張成明, 梁進, 等. 考慮定位力及摩擦力的永磁同步直線電機系統預定位估計算法[J]. 中國電機工程學報, 2021, 41(4): 1496-1504.

[2] 趙牧天, 葛瓊璇, 朱進權, 等. 中速磁懸浮列車分段式長定子永磁直線同步電機牽引控制策略[J]. 電工技術學報, 2022, 37(10): 2491-2502.

[3] 賀玉曉, 王麗梅. 永磁直線同步電動機迭代超螺旋滑模控制[J]. 電氣技術, 2022, 23(6): 24-29.

[4] 武志濤, 楊兆寧. 永磁直線同步電機的雙閉環魯棒補償控制[J]. 電機與控制學報, 2022, 26(3): 101- 108.

[5] 金鴻雁, 趙希梅, 王天鶴. 基于擾動觀測器的永磁直線同步電動機自適應反推互補滑模控制[J]. 中國電機工程學報, 2022, 42(6): 2356-2365.

[6] HUI Yu, CHI Ronghu, HUANG Biao, et al. Extended state observer-based data-driven iterative learning control for permanent magnet linear motor with initial shifts and disturbances[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2021, 51(3): 1881-1891.

[7] 趙希梅, 馬志軍, 朱國昕. 永磁直線同步電機自適應PD型迭代學習控制[J]. 沈陽工業大學學報, 2016, 38(1): 7-12.

[8] FU Xuewei, YANG Xiaofeng, ZANCHETTA P, et al. Frequency-domain data-driven adaptive iterative learning control approach: with application to wafer stage[J]. IEEE Transactions on Industrial Electronics, 2020, 68(10): 9309-9318.

[9] LIU Weike, XU Yunlang, DING Runze, et al. Time- iteration-domain integrated learning control for robust trajectory tracking and disturbance rejection: with application to a PMLSM[J]. IET Control Theory & Applications, 2021, 15(18): 2344-2354.

[10] 張育增, 周睿智, 李帥. 永磁同步直線電機模糊滑模速度控制研究[J]. 電氣技術, 2020, 21(12): 23-29.

[11] 王麗梅, 孫璐, 初升. 基于經驗模態分解算法的永磁直線同步電機迭代學習控制[J]. 電工技術學報, 2017, 32(6): 164-171.

[12] 鄭近德, 應萬明, 潘海洋, 等. 基于改進全息希爾伯特譜分析的旋轉機械故障診斷方法[J]. 機械工程學報, 2023, 59(1): 162-174.

[13] ZHANG Xuejun, HUO Yan, WAN Dongsheng. Improved EMD based on piecewise cubic Hermite interpolation and mirror extension[J]. Chinese Journal of Electronics, 2020, 29(5): 899-905.

[14] 宿文才, 張樹團, 劉陵順. 基于改進極值波延拓的極點對稱模態分解端點效應抑制方法[J]. 電工技術學報, 2020, 35(增刊1): 294-301.

[15] 楊逸帆, 趙兵兵, 康迪, 等. 基于改進希爾伯特-黃變換的電力系統諧波檢測系統設計[J]. 電氣技術, 2022, 23(5): 9-17.

Iterative learning control of linear motor servo system based on modified empirical mode decomposition

LIU Sinuo WU Zhitao

(School of Electronics and Information Engineering, University of Science and Technology Liaoning, Anshan, Liaoning 114051)

In order to address the issue of low convergence speed and poor tracking performance caused by error accumulation effects in iterative learning control of linear motor servo systems, a method based on a modified empirical mode decomposition algorithm is proposed. Firstly, a self-adaptive iterative learning position controller is designed. Subsequently, an improved algorithm based on the extension of triangular extreme wave and complementary set empirical mode decomposition is proposed. This algorithm can decompose the tracking errors of each iteration, screen and eliminate the components that affect error convergence. Through simulation analysis and a comparison with traditional iterative learning control, the paper demonstrates that the proposed method exhibits faster convergence speed and can achieve high-precision tracking control of linear motors with fewer iterations.

permanent magnet linear synchronous motor (PMLSM); iterative learning; modified empirical mode decomposition; convergence speed

2023-12-22

2024-01-08

劉思諾（1999—），男，河北秦皇島人，碩士研究生，主要研究方向為永磁直線同步電機控制。

國家自然科學基金項目（51677122）