給定度序列的連通圖類的k階Sombor指數(shù)

王星雨,耿顯亞

(安徽理工大學 數(shù)學與大數(shù)據(jù)學院,安徽 淮南 232001)

0 引言

G是具有頂點集合V(G)和邊集合E(G)的圖.令d(u)=dG(u),N(u)=NG(u)〔頂點u∈V(G)的鄰域集〕.如果V(G)=(v1,v2,…,vn),di=d(vi),1≤i≤n,則π=(d1,d2,…,dn)被稱為G的度序列.通常假設(shè)d1≥d2≥…≥dn,定義Γ(π)為度序列π的連通圖類.有n個頂點和(n+c-1)個邊的連通圖被稱為c圈圖.

近期,Gutman提出了一個幾何方法來解釋基于度的圖不變量[1],通過這種方法,介紹了Sombor指數(shù),定義為:

后期,這種圖不變性引起了廣泛注意,在一系列研究中確定了它的數(shù)學性質(zhì).

對原始Sombor指數(shù)進行修改,使其變?yōu)楦话愕腟ombor指數(shù)[2-10],定義為:

其中α≠0是實數(shù).顯然SO0.5(G)=SO(G).

確定Γ(π)的元素和圖不變量是很重要的.一些這樣的研究已經(jīng)發(fā)表在相關(guān)文獻上[11-15].這些結(jié)果表明,在許多情況下,極值圖是BFS型的.

1 定理的證明

定義1[10]G是一個連通圖.G被稱為BFS圖,若V(G)中存在頂點v1v2…vn滿足:

(1)d(v1)≥d(v2)≥…≥d(vn)和h(v1)≤d(v2)≤…≤d(vn),h(vi)是vi到v1的距離.

(2) 令v∈N(u)N(w),z∈N(w)N(u)滿足h(v)=h(u)+1,h(z)=h(w)+1.如果uw,則vz.

定義2[14]對于一個給定的c圈度序列π=(d1,d2,…,dn),dn=1,n≥3,如果G是一個BFS圖滿足{v1,v2,v3}構(gòu)成一個三角形,當c≥1時,則G被稱為特殊極圖.

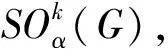
定義3[10]給定度序列π=(d1,d2,…,dn),dn=1,G被稱為連通圖類的k階精確極圖,如果G

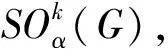
定理2任意圈度序列,有:

(1)TM(π)是c=0時的精確極圖;

(2)UM(π)是c=1時的精確極圖;

(3)BM(π)是c=2時的精確極圖.

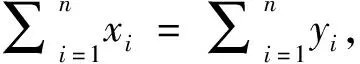
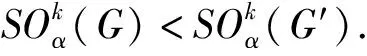
下面證明定理1、定理2.首先引入一個定義在正實數(shù)范圍內(nèi)的對稱二元函數(shù)f(x,y),稱f(x,y)是遞增的(或遞減的),如果滿足

f(x1,x2)+f(y1,y2)≥(≤)f(y1,x2)+f(x1,y2),任意x1≥y1>0,x2≥y2>0,當x1>y1,x2>y2時,上式嚴格不等.

Wang[15]給出了將連通圖和對稱二元函數(shù)f(x,y)聯(lián)系在一起的連接函數(shù)

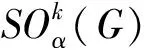
定理1和定理2的證明還需要引入兩個引理.

引理1[14]任意給定度序列π=(d1,d2,…,dn),dn=1,在連通圖類Γ(π)中,存在一個特殊極BFS圖G,使得當f(x,y)遞增時,Mf(G)是最大的,當f(x,y)遞減時,Mf(G)是最小的.

引理2[14]給定c圈度序列π……