基于EWT和NeuralProphet-MLP的蜂窩網(wǎng)絡(luò)流量長期預(yù)測方法

蔣東浩 趙洪華 王真

收稿日期：2023-08-28

DOI：10.19850/j.cnki.2096-4706.2024.06.012

摘? 要：蜂窩網(wǎng)絡(luò)流量長期預(yù)測對網(wǎng)絡(luò)擴展和優(yōu)化具有重要意義，針對長期預(yù)測中數(shù)據(jù)可用性低以及非線性等弊端所帶來的諸多挑戰(zhàn)，提出一種基于分解的分頻預(yù)測模型。分別采用NeuralProphet模型和多層感知機對分解出的低頻分量和中高頻分量進行預(yù)測，最后對各分量預(yù)測結(jié)果進行逆經(jīng)驗小波變換得到最終結(jié)果。在真實的蜂窩網(wǎng)絡(luò)流量數(shù)據(jù)集上進行驗證，結(jié)果表明所提方法相較于傳統(tǒng)預(yù)測模型在準確度上有較大提升，具有較好的應(yīng)用價值。

關(guān)鍵詞：蜂窩網(wǎng)絡(luò)流量預(yù)測；經(jīng)驗小波變換；NeuralProphet模型；多層感知機

中圖分類號：TN929.53；TP18 文獻標識碼：A 文章編號：2096-4706（2024）06-0052-06

Long-term Prediction Method for Cellular Network Traffic Based on EWT and NeuralProphet-MLP

JIANG Donghao， ZHAO Honghua， WANG Zhen

（College of Command and Control Engineering， Army Engineering University of PLA， Nanjing? 210007， China）

Abstract： Long term prediction of cellular network traffic is of great significance for network expansion and optimization. To address the many challenges brought by low data availability and nonlinearity in long-term prediction， a decomposition-based frequency division prediction model is proposed. The NeuroalProphet model and multilayer perceptron are used to predict the decomposed low-frequency components and mid-to-high frequency components， and the final results are obtained by applying inverse empirical wavelet transform to the predicted results of each component. Verification is carried on a real cellular network traffic dataset， the results show that the proposed method has a significant improvement in accuracy compared to traditional prediction models and has good application value.

Keywords： cellular network traffic prediction; empirical wavelet transform; NeuralProphet model; multilayer perceptron

0? 引? 言

提供穩(wěn)定可靠的高質(zhì)量通信服務(wù)是運營商的重要服務(wù)目標。為了實現(xiàn)這一目標，運營商需提前對各區(qū)域未來流量需求進行預(yù)測，及時對網(wǎng)絡(luò)進行管理，避免出現(xiàn)容量瓶頸，保障用戶獲得無處不在的高速網(wǎng)絡(luò)服務(wù)。現(xiàn)有研究中，針對蜂窩網(wǎng)絡(luò)的流量預(yù)測通常被定義為時間序列預(yù)測問題，根據(jù)預(yù)測周期的不同可具體分為短期預(yù)測（秒、分鐘、小時）和長期預(yù)測（天、周、月）。通過不同預(yù)測周期的流量預(yù)測，運營商可以執(zhí)行不同等級的網(wǎng)絡(luò)管理措施。對于短期預(yù)測而言，其預(yù)測結(jié)果可以反映網(wǎng)絡(luò)的臨時波動，進而指導(dǎo)運營商對基站進行一些臨時性調(diào)整（如基站功率設(shè)置、資源調(diào)度）。顯而易見地，臨時性調(diào)整只能應(yīng)對小規(guī)模、突發(fā)性的網(wǎng)絡(luò)波動，無法根本性地解決流量未來增長所導(dǎo)致的網(wǎng)絡(luò)容量不足問題。相比較而言，長期預(yù)測能夠得出未來較長一段時間的流量增長，進而可以預(yù)留更長的時間以進行更加多元的解決方案。

早期的工作中，差分整合移動平均自回歸模型（Autoregressive Integrated Moving Averagemodel， ARIMA）[1]、三次指數(shù)平滑模型（Holt-Winters model， HW）[2]等統(tǒng)計模型被廣泛應(yīng)用在蜂窩網(wǎng)絡(luò)流量預(yù)測問題中。近年來，對復(fù)雜模式具有良好學習能力以及自適應(yīng)性強的深度學習模型被廣泛應(yīng)用于時序預(yù)測問題中。在蜂窩網(wǎng)絡(luò)流量預(yù)測問題上，被廣泛使用的神經(jīng)網(wǎng)絡(luò)主要有長短期記憶網(wǎng)絡(luò)（long short-term memory， LSTM）[3]、門控循環(huán)單元（gated recurrent unit， GRU）[4]、卷積神經(jīng)網(wǎng)絡(luò)（Convolutional Neural Network， CNN）[5]。文獻[6]利用基站間空間合作關(guān)系，構(gòu)建基于LSTM和詞嵌入的流量預(yù)測模型，提高了流量預(yù)測的準確率。文獻[7]將注意力機制引入到CNN中，用于捕獲流量的長期依賴性，在提高精準度的同時縮減了訓(xùn)練時間。

除直接預(yù)測外，分解后預(yù)測也是蜂窩網(wǎng)絡(luò)流量預(yù)測的重要模式。對網(wǎng)絡(luò)流量先進行分解則可以將原始數(shù)據(jù)分解為若干個較為平穩(wěn)的序列，進而增強序列的可預(yù)測性。例如，文獻[8]提出了一種基于張量補全（Tensor Completion， TC）的蜂窩網(wǎng)絡(luò)個體流量預(yù)測方法，TC可以對原始流量數(shù)據(jù)進行缺失值填充的同時，將數(shù)據(jù)分解為兩個分量，然后對兩個分量分別進行預(yù)測。相似的，文獻[9]使用離散小波變換（Discrete Wavelet Transform， DWT）將單用戶流量數(shù)據(jù)進行分解，并對產(chǎn)生的高頻分量和低頻分量分別進行預(yù)測。文獻[10]通過傅里葉分析提取流量數(shù)據(jù)的主導(dǎo)周期成分，利用LSTM對剩余的隨機分量進行預(yù)測，并使用高斯過程回歸對殘差分量進行學習以提高預(yù)測精度。

但是，上述研究集中在對蜂窩網(wǎng)絡(luò)流量進行短期預(yù)測，在長期預(yù)測問題上尚有研究空間。與短期預(yù)測不同，長期預(yù)測依賴于短且有噪聲的時間序列，預(yù)測難度相對較大[11]，因此需要提出新的預(yù)測方法。

在此背景下，本文提出了一種基于EWT和NeuralProphet-MLP的蜂窩網(wǎng)絡(luò)流量長期預(yù)測方法。該方法首先采用經(jīng)驗小波變換（Empirical Wavelet Transform， EWT）對原始流量數(shù)據(jù)進行分解，生成若干個模式相似的多分辨率分析（Multiresolution Analysis， MRA）分量；對于分解出的低頻分量，使用一種多組件預(yù)測模型NeuralProphet進行預(yù)測，該模型具有良好的可解釋性和預(yù)測性能，能夠?qū)Π厔菪缘牡皖l分量實現(xiàn)準確預(yù)測；中高頻分量使用簡單的前饋神經(jīng)網(wǎng)絡(luò)多層感知機（Multilayer Perceptron， MLP）進行預(yù)測，可以在保證預(yù)測性能的前提下減少訓(xùn)練和預(yù)測時間，對中高頻分量的非線性模式進行良好的表征；最后，將預(yù)測所得分量經(jīng)過逆經(jīng)驗小波變換得到最終預(yù)測結(jié)果。本文的貢獻在于：針對蜂窩網(wǎng)絡(luò)流量的長期預(yù)測問題進行了研究，所提預(yù)測方法能夠為蜂窩網(wǎng)絡(luò)的規(guī)劃和優(yōu)化問題提供重要參考；設(shè)計了一種基于分解的蜂窩網(wǎng)絡(luò)流量分頻預(yù)測方法，在解決流量長期預(yù)測中數(shù)據(jù)非平穩(wěn)性問題的基礎(chǔ)上，考慮了不同頻率分量的特性并進行分頻預(yù)測，進一步提升了預(yù)測精度。

1? 問題描述

蜂窩網(wǎng)絡(luò)流量預(yù)測可形式化為時間序列預(yù)測模型，每個固定時間間隔的流量值表示為一個序列值。具體來說，每個區(qū)域的待預(yù)測流量值可由過去一段時間內(nèi)的歷史流量值預(yù)測得出，如式（1）所示：

（1）

其中，k為該模型的預(yù)測步長，n為所使用歷史流量值的總天數(shù)。

本文針對蜂窩網(wǎng)絡(luò)流量進行長期預(yù)測，所設(shè)定的預(yù)測步長為30天。該問題的挑戰(zhàn)在于時間粒度的增大導(dǎo)致可使用歷史數(shù)據(jù)的減少，進而加大了流量的預(yù)測難度。對原始數(shù)據(jù)進行轉(zhuǎn)換后，流量序列的長度相較于原始數(shù)據(jù)縮減24倍。數(shù)據(jù)量的減少增加了噪聲出現(xiàn)的概率，加大了噪聲對序列數(shù)據(jù)的影響。另一方面，隨著預(yù)測步長的增加，歷史數(shù)據(jù)的可用性也將進一步下降。這是由于在實際運營中，過長的時間間隔將導(dǎo)致異常事件的發(fā)生風險，以及網(wǎng)絡(luò)升級等發(fā)生的可能性。

2? 預(yù)測模型設(shè)計

本小結(jié)對設(shè)計的預(yù)測模型進行描述。經(jīng)過對轉(zhuǎn)換后流量數(shù)據(jù)的特性進行分析，發(fā)現(xiàn)其具有非線性、非平穩(wěn)性以及具有一定周期性和節(jié)假日特征。針對以上特點，設(shè)計了基于分解后分頻預(yù)測的模型架構(gòu)。由于低頻分量和中高頻分量分別對應(yīng)序列的趨勢成分和細節(jié)信息，因此采用不同模型進行預(yù)測。其中，低頻分量使用對趨勢成分具有良好擬合能力的NeuralProphet模型，中高頻分量使用對非線性特征表征能力較強的MLP模型。

2.1? 基于EWT的原始數(shù)據(jù)分解

經(jīng)驗小波變換（EWT）[12]是一種基于時域的信號分解方法，為非平穩(wěn)信號的處理提供了新的思路。該方法結(jié)合了經(jīng)驗?zāi)B(tài)分解（Empirical Mode Decomposition， EMD）的自適應(yīng)理念以及經(jīng)典小波變換（Wavelet Transform， WT）的緊框架理論，并具有優(yōu)于EMD方法的理論基礎(chǔ)。EWT方法的基本原理是依據(jù)信號的頻譜特征對其傅里葉譜進行劃分，然后構(gòu)建小波濾波器組，進而提取出信號的AM-FM分量。

給定蜂窩網(wǎng)絡(luò)流量訓(xùn)練集數(shù)據(jù){RT | t = 1，2，…，n}，其中t為序列所包含天數(shù)，R（t）為每日流量值，EWT的具體過程如下：

1）對序列RT進行傅里葉變換，得到支撐區(qū)間在[0，π]范圍內(nèi)的傅里葉頻譜R（ωt）。

2）將頻譜R（ωt）分解為M個頻帶，劃分邊界為ωm （m = 1，2，…，M + 1），每個頻帶為Λm = [ωm-1，ωm] （m = 1，2，…，M）。

3）在分割后的頻帶Λm上利用Littlewood-Paley和Meyer小波的構(gòu)造方法定義帶通濾波器組，確定經(jīng)驗尺度函數(shù)? 和經(jīng)驗小波函數(shù) 。

4）對信號RT進行重構(gòu)，其表達式如式（2）所示：

（2）

式中， 為經(jīng)驗小波逼近系數(shù)， 為經(jīng)驗小波細節(jié)系數(shù)，*為卷積運算。

經(jīng)過以上步驟，原流量序列RT被分解得到若干AF-FM分量Rk（t），頻率由低到高分別為：

（3）

（4）

2.2? 基于NeuralProphet模型的低頻分量預(yù)測

對于分解產(chǎn)生的低頻分量，通常對應(yīng)原始序列的趨勢性信息以及季節(jié)性信息，因此使用對趨勢性信息以及季節(jié)性信息具有良好建模能力的NeuralProphet模型進行預(yù)測。NeuralProphet [13]是一個可擴展、可解釋的時間序列預(yù)測模型，在Prophet [14]模型的基礎(chǔ)上引入了AR-Net用于建模時間序列的自相關(guān)特性。NeuralProphet模型支持不同模塊的組合，用于對不同預(yù)測場景的適應(yīng)性配置。所有模塊在生成相同步輸出的前提下，各模塊有單獨的輸入以及建模過程。NeuralProphet模型將時間序列分解為趨勢項、季節(jié)性項、節(jié)假日項、自回歸項、未來回歸項以及滯后回歸項。本文所使用的模型由式（5）定義為：

（5）

其中，T（t）和S（t）分別為輸入數(shù)據(jù)的趨勢項和季節(jié)項，H（t）為節(jié)假日或異常事件的效應(yīng)函數(shù)，A（t）為時間t的自回歸效應(yīng)。

趨勢項T（t）反映序列的總體變化，通過識別突變點將序列劃分為多個分段，進而擬合出序列的變化趨勢。季節(jié)項S（t）使用傅里葉項對序列的季節(jié)性進行建模，節(jié)假日項H（t）用于擬合節(jié)假日以及異常事件對流量的影響。A（t）為自回歸項，是將變量的未來值與過去值進行回歸的過程。對于低頻分量RLow（T），使用上述模型進行預(yù)測的結(jié)果可表示為：

（6）

2.3? 基于MLP模型的中高頻分量預(yù)測

在分解產(chǎn)生的高頻分量中，包含了流量序列的邊緣以及突變，反映其局部特征。高頻分量非線性特征強，且模式較為復(fù)雜，因此采用MLP對其進行預(yù)測。同時，針對網(wǎng)絡(luò)流量的長期預(yù)測所采用的數(shù)據(jù)量相對較少，復(fù)雜神經(jīng)網(wǎng)絡(luò)容易產(chǎn)生過擬合問題且對流量特征的捕捉能力較差。因此，采用MLP這一簡單人工神經(jīng)網(wǎng)絡(luò)更加適合本文工作場景，且預(yù)測效率相對較高。多層感知器（MLP）是一種前饋人工神經(jīng)網(wǎng)絡(luò)（Artificial Neural Network， ANN）模型，在時間序列預(yù)測問題上廣泛使用。MLP的訓(xùn)練采用反向傳播算法不斷優(yōu)化網(wǎng)絡(luò)權(quán)重，進而最小化預(yù)測誤差。它由多個網(wǎng)絡(luò)層組成，包括輸入層、隱含層和輸出層。其中，輸入層接收樣本數(shù)據(jù)為模型的輸入，隱藏層對輸入數(shù)據(jù)進行處理，其輸出作為下一層的輸入，最終輸出層根據(jù)所需任務(wù)對結(jié)果進行輸出。對于隱含層的神經(jīng)元，執(zhí)行如下運算：

（7）

其中，σ為激活函數(shù)，W（i）（i = 1，2）為全連接層權(quán)重矩陣，b（i）（i = 1，2）為偏置向量，x為輸入層的輸入向量，h（i）為隱含層的輸出。

本文設(shè)計一個雙隱含層的MLP模型用于對中高頻分量的預(yù)測，第一個隱含層神經(jīng)元數(shù)量為64，第二個隱含層神經(jīng)元數(shù)量為128。針對中高頻分量的非線性特性，選擇激活函數(shù)σ為ReLU函數(shù)，捕捉分量中的非線性模式以及特征。經(jīng)過上述MLP模型的預(yù)測，中高頻分量RMid-High（T）被預(yù)測為：

RMid-High（T + K） = σ2（W （2）σ1（W （1）·x + b（1）） + b（2）） （8）

2.4? 預(yù)測框架

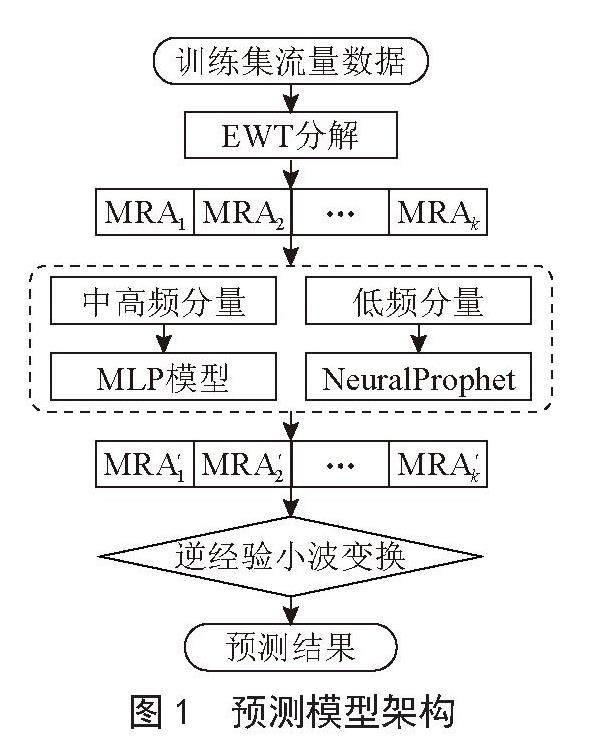
基于EWT和NeuralProphet-MLP的蜂窩網(wǎng)絡(luò)長期流量預(yù)測模型結(jié)構(gòu)如圖1所示。首先將原始流量數(shù)據(jù)劃分為訓(xùn)練集和測試集，將訓(xùn)練集數(shù)據(jù)進行EWT分解，生成k個MRA分量；計算每個分量的過零率，設(shè)置閾值對分量進行分類；對于分解出的低頻分量，使用NeuralProphet模型進行預(yù)測；對于分解出的中高頻分量，使用MLP模型進行預(yù)測；將預(yù)測模塊輸出的預(yù)測值組合成重構(gòu)模塊所需的數(shù)據(jù)格式，使用逆經(jīng)驗小波變換重構(gòu)成最終預(yù)測流量值。

圖1? 預(yù)測模型架構(gòu)

3? 實驗分析

為分析EWT-NeuralProphet-MLP的預(yù)測性能，在三個區(qū)域的真實蜂窩網(wǎng)絡(luò)流量值上進行了實驗驗證。在對比實驗之前，分析了EWT對原始流量數(shù)據(jù)的分解效果。將EWT-NeuralProphet-MLP模型與目前廣泛應(yīng)用的LSTM、SARIMA進行對比，并驗證使用MLP和NeuralProphet不同組合模型的有效性。

3.1? 數(shù)據(jù)集

本文采用的數(shù)據(jù)集來自AIIA杯人工智能巡回賽中國移動“家·網(wǎng)”賽站智能網(wǎng)絡(luò)決賽中的網(wǎng)絡(luò)流量預(yù)測賽題。該數(shù)據(jù)集以小時為粒度，記錄了自2017年1月1日0時至2018年11月15日23時的流量數(shù)據(jù)。其中共包含A、B、C三個區(qū)域，每個區(qū)域的流量數(shù)據(jù)為一個序列[15]。經(jīng)過對該數(shù)據(jù)集的分析，未發(fā)現(xiàn)缺失值，且序列中異常值數(shù)量不顯著。為使得數(shù)據(jù)匹配對未來30天的流量進行預(yù)測需求，需將原始數(shù)據(jù)轉(zhuǎn)換為以天為粒度的流量序列。經(jīng)過數(shù)據(jù)轉(zhuǎn)換，數(shù)據(jù)集由3個長度為683的流量序列組成。該數(shù)據(jù)集經(jīng)過以下方式得出：

1）將序列{RT | t = 1，2，…，n}轉(zhuǎn)換為i個子序列 ，其中i為原序列所包含的天數(shù)。

2）選取每個子序列? 中流量值最大的一個小時的流量Ri（t）。

3）將Ri（t）按序填充至新的序列 ，時間戳信息保留至日級別。

經(jīng)過轉(zhuǎn)換，原序列的每小時流量被轉(zhuǎn)換為每天的自忙時流量，更加符合網(wǎng)絡(luò)擴容工作的場景需要。

3.2? 實驗設(shè)置

將本文所設(shè)計的蜂窩網(wǎng)絡(luò)流量長期分頻預(yù)測模型在上述數(shù)據(jù)集上進行實驗評估。將2017年1月1日至2018年9月16日的流量用作訓(xùn)練集，2018年09月17日至2018年10月16日共計30天的流量數(shù)據(jù)作為測試集。首先，對訓(xùn)練集數(shù)據(jù)作標準化處理后進行EWT分解，分解后的分量通過測算過零率確定低頻與中高頻的邊界，邊界值設(shè)為0.015。然后，使用NeuralProphet模型對低頻分量進行預(yù)測，模型所激活模塊如前所述。對于中高頻分量，使用MLP模型對其進行預(yù)測，每次迭代使用30天歷史流量值，輸出未來7天預(yù)測流量值。經(jīng)過滑動窗口5次迭代預(yù)測，選取前30天網(wǎng)絡(luò)流量作為最終預(yù)測結(jié)果。

實驗評估主要從兩個方面展開：一是與廣泛采用的時間序列預(yù)測模型LSTM和SARIMA模型進行對比，評估本文所提方法的預(yù)測性能；二是將本文方法中所使用模型進行不同組合，驗證分解后預(yù)測以及分頻預(yù)測的有效性。

為對預(yù)測模型的性能進行評估，采用平均絕對百分比誤差（MAPE）和均方根誤差（RMSE）作為評價指標。這兩項指標越小，所表示的預(yù)測結(jié)果精準度越高。其定義如下：

（9）

（10）

式中，N為預(yù)測值個數(shù)，i為預(yù)測值編號，yi為真實值， 為預(yù)測值。

實驗基于硬件環(huán)境Intel Core i5-13500 CPU@3.50 GHz，12核，16 GB內(nèi)存；主要軟件環(huán)境Python 3.6.13，PyTorch 1.10.2，NeuralProphet 0.4.1。

3.3? EWT分解結(jié)果分析

將原流量數(shù)據(jù)進行預(yù)處理后，使用EWT對其進行分解。該分解方法基于小波分析進行構(gòu)造，其分解結(jié)果對分解層數(shù)敏感。因此，設(shè)置合理的分解層數(shù)，對于分解效果以及后續(xù)的預(yù)測效果具有重要影響。分解層數(shù)越大，分解后的形成的子頻帶數(shù)量越大，頻率分辨率越高，隨之時間分辨率降低。經(jīng)過實驗，將時間序列分解為4個模態(tài)分量，并使用locmaxmin方法（即使用傅里葉頻譜中兩個極大值之間的極小值所對應(yīng)的頻率）確定邊界頻率時獲得最佳效果。分解后的模態(tài)分量代表了原始序列不同的特征尺度，更加有利于理解原始序列的局部特征以及全局特征。原始流量數(shù)據(jù)如圖2所示，圖3是對A區(qū)域流量數(shù)據(jù)進行EWT分解后的結(jié)果。

圖2? A區(qū)域原始流量數(shù)據(jù)

圖3? A區(qū)域原始流量的EWT分解結(jié)果

由圖3可知，原始流量被分解為4個MRA分量，顯示了流量序列的不同尺度上的頻率分量。其中，MRA1頻率最小，且總體平緩，體現(xiàn)了該區(qū)域流量的趨勢變化。MRA2和MRA3頻率有所增大，并有一定的周期性特征。MRA4頻率顯著增加，且隨機性較強，預(yù)測難度相比較大。綜上，EWT分解取得了預(yù)期效果，較好地分解出了流量數(shù)據(jù)的趨勢性、周期性以及局部突發(fā)性。

3.4? 對比分析

3.4.1? 預(yù)測結(jié)果對比

SARIMA模型和LSTM模型是時間序列預(yù)測研究中經(jīng)典的預(yù)測模型，故本文采用這兩種模型作為對比模型。對于SARIMA模型，采用自適應(yīng)的方式確定參數(shù)，輸出步長為30。采用的LSTM模型包含3個LSTM層，使用Adam和均方誤差作為損失函數(shù)，觀測窗口長度為30，輸出步長為7。采用滾動預(yù)測的方式對網(wǎng)絡(luò)流量迭代預(yù)測5次，選取前30個預(yù)測值作為預(yù)測結(jié)果。

三種模型的預(yù)測性能對比如圖4和圖5所示。相較于LSTM和SARIMA模型，本文所提出方法的MAPE值和RMSE值相比均有不同程度的下降。此外，由圖6中的擬合曲線可知，LSTM模型和SARIMA模型的預(yù)測結(jié)果對真實流量的波動性擬合效果較差。因此，本文所提出模型的預(yù)測性能優(yōu)于對比模型。

3.4.2? 不同組合模型預(yù)測結(jié)果對比

為了驗證分頻預(yù)測方法的有效性，將各模型進行不同的組合預(yù)測網(wǎng)絡(luò)流量，并比較MAPE和RMSE評估本文方法的預(yù)測性能。對比結(jié)果如表1所示，EWT-NeuralProphet-MLP模型在對各區(qū)域進行預(yù)測時均獲得最佳效果。其中，各區(qū)域預(yù)測結(jié)果的MAPE和RMSE值最大的模型均為NeuralProphet。結(jié)合圖7中預(yù)測結(jié)果的擬合曲線，NeuralProphet模型對流量的走勢模擬效果最佳，但結(jié)果誤差相對較大。同時，預(yù)測結(jié)果表明，對流量序列的分解增強了各模型的預(yù)測性能，基于分解的預(yù)測模型均優(yōu)于原單一模型。EWT-NeuralProphet-MLP模型和EWT-NeuralProphet的對比表明分頻預(yù)測的思想有助于蜂窩網(wǎng)絡(luò)流量的長期預(yù)測，在誤差水平和擬合能力上均有明顯提升。

圖4? 不同預(yù)測方法的MAPE值對比圖

圖5? 不同預(yù)測方法的RMSE值對比圖

圖6? EWT-NeuralProphet-MLP模型與LSTM、SARIMA預(yù)測

結(jié)果對比

圖7? 不同組合模型預(yù)測結(jié)果對比

從不同區(qū)域的角度觀察，各模型在A區(qū)域的預(yù)測性能表現(xiàn)相對較差，在C區(qū)域的預(yù)測性能表現(xiàn)最佳。原始數(shù)據(jù)的模式存在一定關(guān)聯(lián)，A區(qū)域網(wǎng)絡(luò)流量值相對較大且平穩(wěn)性較差，C區(qū)域網(wǎng)絡(luò)流量值相對小且平穩(wěn)性較好，導(dǎo)致各區(qū)域的數(shù)據(jù)可預(yù)測性存在一定差別。

4? 結(jié)? 論

本文針對蜂窩網(wǎng)絡(luò)流量長期預(yù)測面臨的不確定性和復(fù)雜模式等挑戰(zhàn)，提出一種網(wǎng)絡(luò)流量時間序列分頻預(yù)測方法。該方法利用EWT分解模型將原始網(wǎng)絡(luò)流量序列分解為若干MRA分量后，分別使用NeuralProphet和MLP模型對低頻分量和中高頻分量進行預(yù)測。在此基礎(chǔ)上，加入動態(tài)參數(shù)調(diào)整模塊，進一步提升了預(yù)測精確度。通過多組對比實驗表明，本文所提出的方法具有優(yōu)于其他模型的預(yù)測性能，且各組件均對預(yù)測模型的性能有提升效果。

下一步的研究中，將探索使用多源數(shù)據(jù)融合對蜂窩網(wǎng)絡(luò)流量進行預(yù)測，以提升預(yù)測精確度。

參考文獻：

[1] SHU Y T，YU M F，LIU J K， et al. Wireless traffic modeling and prediction using seasonal ARIMA models [J].IEEE International Conference on Communications，2003，E88-B（10）：3992-3999.

[2] TIKUNOV D，NISHIMURA T. Traffic prediction for mobile network using Holt-Winter's exponential smoothing [C]//2007 15th International Conference on Software，Telecommunications and Computer Networks.Split：IEEE，2007：1-5.

[3] AZARI A，PAPAPETROU P，DENIC S，et al. Cellular Traffic Prediction and Classification： A Comparative Evaluation of LSTM and ARIMA [C]//International Conference on Discovery Science.[S.I.]：Springer， Cham，2019，11828：124-129.

[4] MAHDY B，ABBAS H，HASSANEIN H S，et al. A Clustering-Driven Approach to Predict the Traffic Load of Mobile Networks for the Analysis of Base Stations Deployment [J/OL].Journal of Sensor and Actuator Networks，2020，9（4）：53[2023-07-20].https：//doi.org/10.3390/jsan9040053.

[5] GAO Y，ZHANG M，CHEN J J，et al. Accurate Load Prediction Algorithms Assisted with Machine Learning for Network Traffic [C]//2021 International Wireless Communications and Mobile Computing （IWCMC）.Harbin City：IEEE，2021：1683-1688.

[6] 彭鐸，周建國，羿舒文，等.基于空間合作關(guān)系的基站流量預(yù)測模型 [J].計算機應(yīng)用，2019，39（1）：154-159.

[7] SHEN W X，ZHANG H X，GUO S S，et al. Time-Wise Attention Aided Convolutional Neural Network for Data-Driven Cellular Traffic Prediction [J].IEEE Wireless Communications Letters，2021，10（8）：1747-5171.

[8] LIU C，WU T，LI Z，et al. Individual Traffic Prediction in Cellular Networks Based on Tensor Completion [J/OL].International Journal of Communication Systems，2021，34（16）：e4952[2023-07-20].https：//doi.org/10.1002/dac.4952.

[9] LI Y，MA Z A，PAN Z W，et al. Prophet Model and Gaussian Process Regression Based User Traffic Prediction in Wireless Networks [J].Science China （Information Sciences），2020，63（4）：207-214.

[10] WANG W，ZHOU C H，HE H L，et al. Cellular Traffic Load Prediction with LSTM and Gaussian Process Regression [C]//ICC 2020-2020 IEEE International Conference on Communications （ICC）.Dublin：IEEE，2020：1-6.

[11] GIJóN C，TORIL M，LUNA-RAMíREZ S，et al. Long-Term Data Traffic Forecasting for Network Dimensioning in LTE with Short Time Series [J/OL].Electronics，2021，10（10）：1151[2023-07-26].https：//doi.org/10.3390/electronics10101151.

[12] GILLES J. Empirical Wavelet Transform [J].IEEE Transactions on Signal Processing，2013，61（16）：3999-4010.

[13] TRIEBE O，HEWAMALAGE H，PILYUGINA P，et al. NeuralProphet： Explainable Forecasting at Scale [J/OL].arXiv：2111.15397 [cs.LG].[2023-07-20].https：//doi.org/10.48550/arXiv.2111.15397.

[14] TAYLOR S J，LETHAM B. Forecasting at Scale [J].The American Statistician，2018，72（1）：37-45.

[15] GUO D，XIA X W，ZHU L，et al. Dynamic Modification Neural Network Model for Short-term Traffic Prediction [J].Procedia Computer Science，2021，187：134-139.

作者簡介：蔣東浩（1999—），男，漢族，山東濟寧人，碩士研究生，研究方向：網(wǎng)絡(luò)智能規(guī)劃；通訊作者：趙洪華（1979—），男，漢族，河北吳橋人，副教授，博士，研究方向：網(wǎng)絡(luò)管理、網(wǎng)絡(luò)智能規(guī)劃。