基于BSFLA-BiGRU-Attention短期電力負荷預測

華北電力大學控制與計算機工程學院 羅 毅 吳佳瑋

隨著“碳達峰”“碳中和”概念的提出，新能源裝機容量不斷提高，電力系統現有平衡機制受到挑戰，構建新型電力系統迫在眉睫[1]。為了深入了解各個地區用電需求，合理安排新能源裝機容量，以匹配發電與負荷雙向不確定因素，實現新形態下的電力系統平衡，負荷預測工作的準確度有必要進一步提升。

由于電力負荷受天氣、節假日等因素影響較大、隨機性較強，經典傳統方法如回歸分析法、時間序列法等已無法滿足預測精度要求，支持向量機法、神經網絡法[2]等智能算法逐漸成為當前負荷預測方法的主流。支持向量機法難以訓練大規模數據集，參數和核函數選擇復雜[3]。神經網絡算法有著較為良好的非線性映射能力、高度的自適應自學習能力、良好的泛化能力，以及容錯能力，被廣泛應用于負荷預測，但當數據較多時易出現“長期依賴”，影響預測效果，長短期記憶（Long Short Term Memory， LSTM）神經網絡可有效解決此問題[4]。改進后的門控循環單元（Gated Recurrent Unit， GRU）網絡在預測結果相近的情況下，擁有更為簡潔的結構與參數[5]。

為了解決GRU 網絡參數選擇過于主觀的問題，并最大化利用已有信息，提升預測精度，本文建立了一種新的負荷預測模型，針對智能優化算法中的混合蛙跳算法進行改進，以此優化神經網絡超參數，將當日天氣、是否為工作日等作為影響負荷的因素納入考慮，并用注意力機制對輸出進行處理，從而提高短期電力負荷預測準確度。

1 模型原理

1.1 混合蛙跳算法及其改進

粒子群算法（Particle Swarm Optimization，PSO）作為最早被提出的群智能優化算法，其理論不夠完善，在實際搜索過程中易陷入局部最優。混合蛙跳算法（Shuffled Frog Leaping Algorithm,SFLA）參數更少、全局搜索能力更強[6]。

在覓食過程中，青蛙總數為F，子群數為m，每個子群內青蛙個數為n，即三者滿足關系式F=m×n。記子群內最優個體為Pb，最差個體為Pw，全局最優個體為Pg，對應適應度分別為Fb、Fw、Fg，青蛙每次的更新步長為D。每個子群內青蛙個體更新公式見式（1）。

式中，r為[0,1]內的隨機數，更新步長D由隨機數r與子群內最優個體Pb及最差個體Pw之差決定。如果更新后的青蛙適應度比原有適應度好則保留，如并未得到改善則利用全局最優個體Pg通過式（2）再次進行更新。

如二次更新后適應度仍未得到改善，則隨機生成一個新的個體取代原有個體。詳細算法流程如下。

第一，初始化相關參數，確定各參數定義域、青蛙總數、子群數、更新步長、進化次數等。第二，初始化青蛙群，隨機生成F個個體并按適應度排序，依次分配到m個子群中，排名1～m的個體分別進入第1～m個子群，m+1～2m的個體同理，以此類推，直至所有個體分配完畢。第三，選出全局最優個體Pg，每個子群內最優個體Pb及最差個體Pw，根據公式對子群內的青蛙進行局部更新，重復此操作直至達到子群進化次數。第四，將更新后的子群混合，重新計算適應度，并重復第三步，直至達到全局最大循環次數，輸出Pg及Fg。

基礎的混合蛙跳算法由于每次只更新子群內最差青蛙的位置，導致算法收斂速度較慢，且容易陷入局部最優，基于此對混合蛙跳算法進行改進。與原有混合蛙跳算法相比，改進的混合蛙跳算法青蛙總數及子群劃分不變，原來的局部更新改進為除子群最優個體外全部更新，即對于非最優的個體進行批量更新，記為批處理混合蛙跳算法。BSFLA 更新后見式（3）。

式中，r為[0,1]內的隨機數，Pb為子群內最優個體，Pr為子群內其余個體，更新步長D由隨機數r與子群內最優個體Pb及其余個體Pr之差決定。如果更新后的青蛙適應度比原有適應度好則保留，如并未得到改善則利用全局最優通過式（4）再次進行更新。

如二次更新后仍未改善則隨機生成一個新的個體替代原個體。

為了更直觀地展示BSFLA 尋優效果，現采用Rastrigin 函數對兩種算法進行尋優能力測試。Rastrigin 函數公式見式（5）。

式中，d為變量維度，此處d=2，xi（i=1，2，…，d）表示多維變量。Rastrigin 函數全局最小值為0，具有多個局部極小值，極易陷入局部最優，可用作檢測算法跳出局部最優的能力。

BSFLA 及SFLA 在Rastrigin 函數中尋優結果如圖1所示。可以看出，BSFLA 的收斂速度較快，且多次跳出局部最優值，在約350次迭代時成功找到全局最小值0。

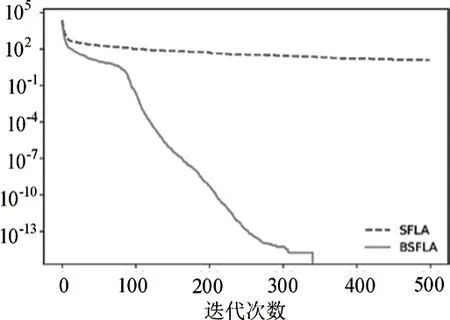
圖1 尋優能力對比

1.2 門控循環單元

LSTM 常用于處理序列信號，但參數多，計算所需內存較大，存在過擬合風險。GRU 將LSTM結構中的遺忘門和更新門合并為一個更新門，用以對上一個時刻和此時的輸入值進行選擇性保留。在最終預測結果相近的情況下，GRU 比LSTM 減少一個門，參數數量有所降低，降低了過擬合和“梯度爆炸”風險，極大地節約了計算時間。綜合上述因素，本篇選擇GRU 作為最終訓練網絡，其基本單元結構如圖2所示。圖中xt為輸入向量，ht-1為上一單元輸出，ht為當前單元輸出，σ、tanh 代表使用的激活函數Sigmoid 和tanh，圖中“＊”代表矩陣對應元素相乘。Γu、Γr為門控單元，二者取值范圍均為[0,1]；Γu越大，新信息的占比就越多。

圖2 GRU 基本單元

在模型訓練過程中，Γu會自動更新以尋找最優值，從而擺脫梯度消失現象。對應表達式見式（6）。

式中，Wu、Wr、Wh為對應權重，為模塊之間的記憶單元，“·”代表矩陣相乘。

雙向門控循環單元在GRU 的基礎上進行了一定改進，可視作兩個單向GRU 的組合。其輸出不僅與歷史信息有關，也受到未來信息的影響，這種雙向結構有助于神經網絡充分利用現有信息，進一步提升預測精度。其結構如圖3所示。

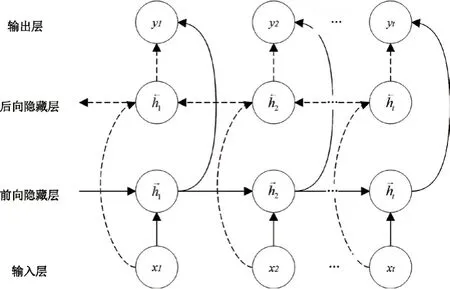
圖3 BiGRU 神經網絡結構

圖中xi（i=1，2，3，…，t）為輸入，（i=1，2，3，…，t）為前向傳播隱藏狀態，（i=1，2，3，…，t）為反向傳播隱藏狀態，yi（i=1，2，3，…，t）為對應輸出，其內部計算公式見式（7）。

式中，wt、vt分別表示t時刻、對應的權重，bt為t時刻yt對應偏置量。

1.3 Attention 機制原理

Attention 機制通過模擬人腦處理信息的方式，可有效提高訓練效果，實現信息資源的最優利用。負荷數據具有相似性，引入Attention 機制可以更好地對歷史數據信息進行學習。本文所用Attention 基本結構如圖4所示。圖中xi（i=1，2，3，…，t）為輸入，（i=1，2，3，…，t）為前向傳播隱藏狀態，（i=1，2，3，…，t）為反向傳播隱藏狀態，αi（i=1，2，3，…，t）為Attention 機制計算所得權重，y為對應輸出。

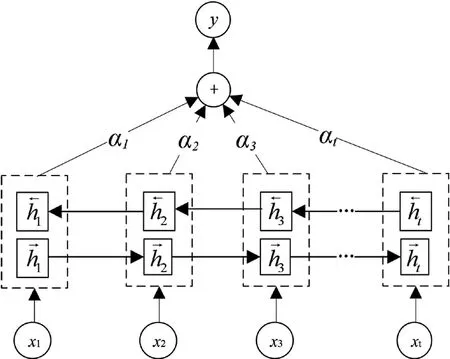
圖4 Attention 機制結構

Attention 機制內部計算公式見式（8）～式（10）。

式中，et為t時刻輸入和輸出的匹配度，u、w為權重系數，b為偏置量；αt為歸一化后的權值；yt為經加權后求得的輸出。

2 基于BSFLA-BiGRU-Attention 的負荷預測模型

2.1 預測模型敘述

在神經網絡算法中，超參數往往由網格法或經驗法確定，此種方法不僅難以找到最優解，也缺乏客觀性和嚴謹性。PSO 作為最經典的群智能優化算法，難以找到全局最優解。本文引入混合蛙跳算法，該算法參數更少，尋優能力更強，且在此基礎上對SFLA 進行改進，以達到更佳的尋優能力。

GRU 通過引入門控單元，有效解決了數據特征難以尋找的問題；在此基礎上，BiGRU 相比GRU增加了反向傳播過程，能更好地提取未來負荷中包含的關聯信息，提升預測精度。Attention 機制通過更改分配在各個隱藏狀態上的權重，合理利用歷史負荷數據，強化了關鍵數據對預測結果的影響。

2.2 預測模型結構

本文模型由輸入層、BiGRU 層、Attention 層、輸出層組成，其結構如圖5所示。歷史負荷數據作為輸入進入BiGRU 網絡進行學習，BiGRU 層對輸入數據進行特征提取，采用Adam 算法對其進行優化。BiGRU網絡隱藏層的最終狀態作為輸出進入Attention 層，Attention 機制根據上文公式自動分配權重，迭代選出最優權重矩陣，加權求和得到最終輸出。

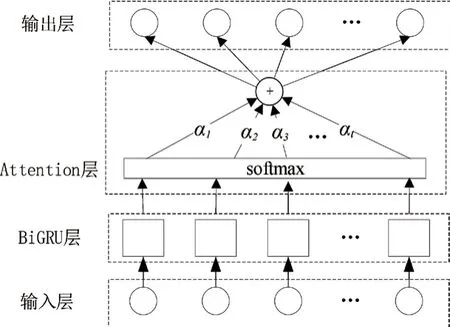
圖5 BSFLA-BiGRU-Attention 模型結構

2.3 預測模型敘述

影響GRU 訓練效果的參數主要有三個，即隱藏神經元個數、隱藏層數，以及訓練次數，將這三個變化量作為青蛙個體特征，選取部分數據集進行訓練，適應度函數定義為均方誤差（Mean Square Error, MSE），見式（11）。

訓練過程中相關參數設置見表1。

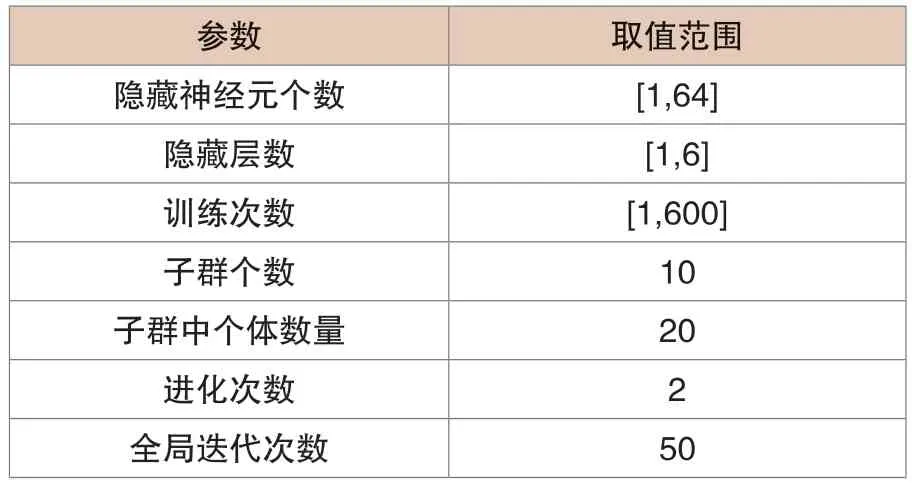
表1 參數設置

3 算例分析

本文選取第九屆“中國電機工程學會杯”全國大學生電工數學建模競賽A 題所提供的標準數據集中某地區2012年1月10日至2015年1月10日的電力負荷數據，采樣間隔為15分鐘，每日96個數據點，包含天氣因素（如日最高溫、日最低溫、日平均溫度、相對濕度等信息）及日期類型數據。

3.1 數據預處理

為了保證預測結果的準確性，首先需要對負荷數據進行預處理。根據電力負荷具有的連續性和日相似性及周相似性對數據分別做水平預處理及垂直預處理，波動過大的數據以前后時刻或前后天此刻的平均值參與訓練。

負荷數據受日期類型、當日氣溫等因素影響較大，因此將相關氣象因素納入考慮。另外，由于電力負荷與溫度、濕度等氣象因素不屬同一量級，如不加處理直接進行訓練，容易導致GRU 只注重負荷信號，而忽略了其他因素對預測結果的影響，因此需對負荷值及溫度進行歸一化處理；濕度數據本身即為相對濕度，取值范圍為[0,1]，無須處理。歸一化公式見式（12）。

鑒于工作日和節假日負荷呈現出較大區別，特對負荷所屬日期類型進行劃分，周一至周五記為0.1，周六記為0.5，周日及節假日記為1。

3.2 仿真分析

為驗證上述模型的科學性及有效性，選取該地區2014年11月20日至2015年1月10日的電力負荷數據作為數據集，其中11月20日至12月31日為訓練集，1月1日至1月3日為驗證集。為全面體現預測效果，將2015年1月4日至1月10日共一周的數據作為預測集對預測結果進行校驗。

模型誤差采用平均絕對百分比誤差yMAPE（Mean Absolute Percentage Error, MAPE）和準確率A進行評判。平均絕對百分比誤差計算方法見式（13）。

準確率計算方法見式（14）、式（15）。

本文所建立模型的七日預測結果如圖6所示。

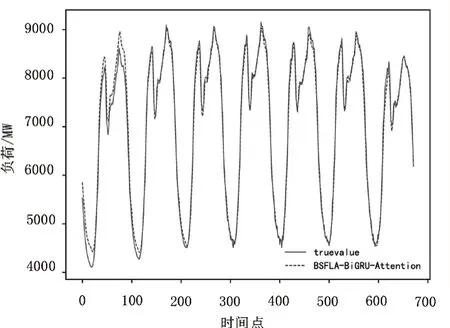
圖6 本文模型負荷預測曲線

為全面展示本文所提模型尋優效果，另加入PSO 算法和基于麻雀搜索算法（Sparrow Search Algorithm, SSA）的最小二乘支持向量機（Least Squares Support Vector Machine, LSSVM）模型[7]進行對比，分別用PSO、SFLA 和對GRU 參數進行尋優，將尋優結果代入模型進行計算，并與本文所建立模型進行對比。各模型評判結果見表2。

表2 各模型預測對比（%）

從預測結果平均值角度分析，本文所提出的模型擁有最低誤差1.705%和最高準確度97.57%。相比于其他模型，本文模型預測誤差分別降低了2.183%、1.574%和0.568%，且1月6日至1月10日本文模型誤差均在1.2%左右，可見本文模型與其他模型相比有顯著優勢。為更清晰表明該模型預測效果，表3給出了該算法1月10日部分時間點真實值與預測值對比，并用yMAPE和平均絕對誤差yMAE（Mean Absolute Error, MAE）對模型預測誤差進行評判。平均絕對誤差計算方法見式（16）。

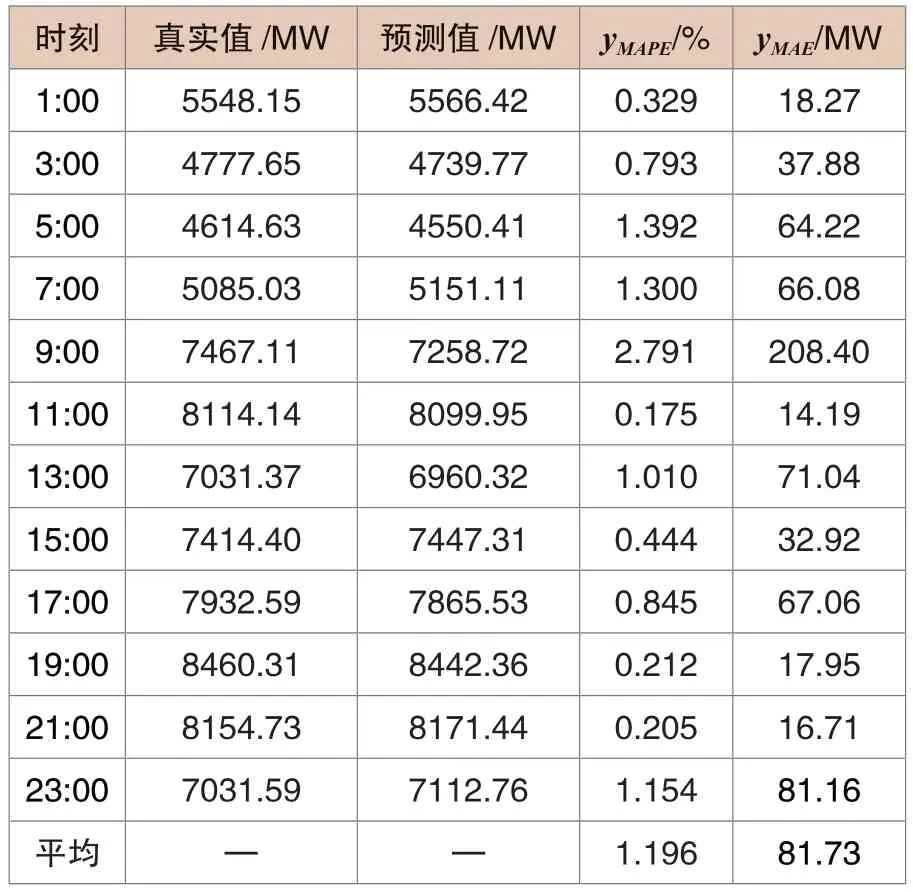
表3 1月10日預測誤差對比

為了更加直觀地展示本文模型的預測效果，給出各模型1月10日的負荷預測曲線，如圖7所示。從圖中可以看出，本文所提模型在幾種模型中具有最好的預測效果。

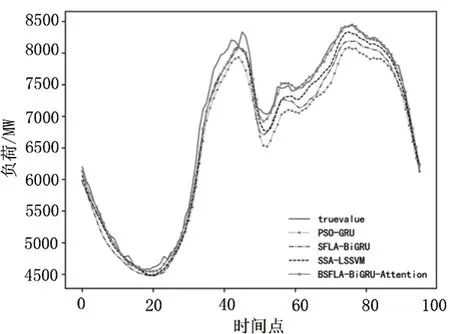
圖7 1月10日預測曲線結果對比

4 結語

本文針對15分鐘粒度的短期電力負荷預測，建立了一種基于注意力機制和BSFLA 算法的BiGRU 預測模型。該方法通過BSFLA 算法優化BiGRU 相關神經網絡參數，利用Attention 機制重新分配輸出權重，并將天氣及工作日等因素納入考慮，從而提高原有模型精度。與傳統SFLA 算法相比，BSFLA 算法的收斂速度更快，更易跳出局部最優點，尋優效果更佳。將該模型與基礎PSO-GRU 和SFLA-BiGRU、SSA-LSSVM 的預測結果進行多項誤差對比得出，改進后的BSFLA-BiGRU- Attention 模型在單日及平均預測結果上均可有效提高負荷預測準確度。

目前較多地區每日負荷仍呈現“雙峰”型，本文所提出的模型可作為參考協助新能源站和水電站提前安排次日、次周發電計劃，削峰填谷，平滑日負荷曲線，以較低的經濟損失實現能源的最大化利用。