螺紋牙環形受剪力學模型研究

摘 要：以材料力學、彈性力學理論為依據，以試驗結果為分析基礎，根據GB/T 3098.2—2015《緊固件機械性能 螺母》標準規定內螺紋高度（螺母厚度）H≥0.8D以及螺紋斷裂形貌特征，對螺紋懸臂梁假設進行探討。提出螺紋懸臂梁假設不符合材料力學、彈性力學懸臂梁結構定義，按懸臂梁假設采用材料力學的彎曲應力和剪切應力公式，不符合實驗結果。在此基礎上，提出螺紋環形受剪力學模型，認為螺紋主要受剪力，只校核切應力τ≤[τ]（[τ]為許用剪切應力）即可滿足螺紋設計要求。同時采用科學類比方法，發現內外螺紋（牙）受力等效于墊圈沖孔力學應力狀態，可以借用墊圈沖孔來進行對比分析。通過材料力學解析，分析推導了螺紋（牙）環形受剪力學公式，提出旋擰過載時螺紋剪斷還是螺桿斷裂判決不等式。依據受剪公式及判決不等式發明了一種基于強度理論的自鎖螺母，按國軍標GJB 715.3A—2002《緊固件試驗方法 振動》進行振動試驗，該螺母鎖緊性能超過了標準要求，從而證明了螺紋（牙）環形受剪力學模型的正確有效性。

關鍵詞：螺紋牙；懸臂梁；環形受剪；類比法

中圖分類號：TG51；TH131? ? 文獻標志碼：A? ? 文章編號：1671-0797（2024）10-0024-08

DOI：10.19514/j.cnki.cn32-1628/tm.2024.10.007

0? ? 引言

緊固件是用于把兩個或兩個以上的零件（構件）連接成一個整體的機械零件，發展到今天緊固件已形成包括螺栓、螺柱（樁）、螺釘、螺母、墊圈、鉚釘、銷、擋圈和嵌入件等在內的一系列產品。其中，螺紋連接構造簡單、成本較低、安裝方便，使用不受被連接材料限制，因而應用廣泛。

螺栓、螺母或內外螺紋構件，其連接設計要求（目標）主要根據被連接件的具體要求而定。選擇螺栓（外螺紋）、螺母（內螺紋）類型和結構時，要保證足夠的承載能力，要滿足裝拆的方便性或不拆卸的要求，以確保質量檢驗的便利性[1]。應按有關設計手冊計算，以保證足夠的承載能力，一旦選擇了螺栓（外螺紋）、螺母（內螺紋）和螺紋連接副，其各自的性能強度應符合GB/T 3098.1—2010《緊固件機械性能 螺栓、螺釘和螺柱》、GB/T 3098.2—2015《緊固件機械性能 螺母》規定的性能等級。螺栓（外螺紋）、螺母（內螺紋）連接副的性能等級搭配設計應符合GB/T 3098.2—2015“螺母性能等級與搭配使用的螺栓、螺釘或螺柱的最高性能等級”或HB 6443—2008《螺母通用規范》“螺母的強度等級等于與該螺母相配的最高性能等級的螺栓的抗拉強度”附錄A“螺母強度等級”規定，上述兩個螺母標準共同點是連接件搭配螺母的性能等級等于與螺母相配的最高性能等級的螺栓（外螺紋）件性能等級，這樣可以充分發揮螺栓的強度性能，并可提供一個最大的預緊力。對螺紋按標準選取，不用校對螺紋強度；若不按標準選取，需要校對螺紋強度。對螺紋連接的設計，通常希望在超擰的情況下，螺栓、螺母連接副中，螺桿斷裂是預期的失效形式（GB/T 3098.2—2015附錄A）。

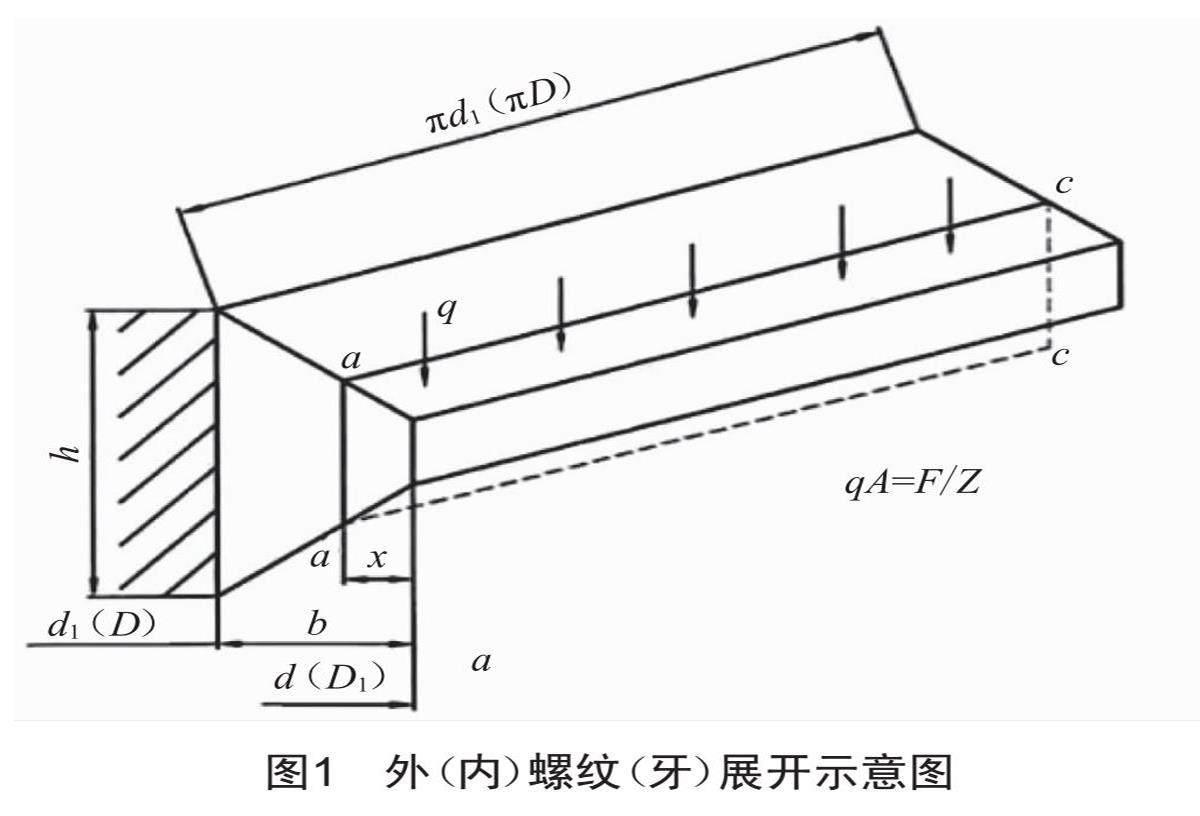
由于對精確度了解不夠，目前為保證零件連接可靠性，在設計時只得用降低許用應力或設定一個系數的方法來校核。而螺紋（牙）校核主要是采用Sopwith和Yamatoto提出的將螺紋展開看成懸臂梁（圖1）的理論[2-5]，按懸臂梁結構假設進行彎曲、剪切、擠壓，應力分別按材料力學解析法進行校核，不超過各自許用應力，即螺紋（牙）滿足安全強度條件。那么這種校核符合實際嗎？能發揮材料的潛力嗎？螺紋展開類似懸臂梁嗎？

本文以材料力學、彈性力學理論為依據，以試驗結果為分析基礎，根據GB/T 3098.2—2015標準規定內螺紋高度（螺母厚度）H≥0.8D、螺紋有效長度≥0.6D（D為內螺紋基本大徑）以及螺紋斷裂形貌特征，對螺紋懸臂梁假設進行探討，提出螺紋懸臂梁假設不符合材料力學、彈性力學定義懸臂梁的要素，采用材料力學的懸臂梁彎曲應力、剪切應力公式，不符合試驗結果。在此基礎上，筆者提出了螺紋環形受剪力學模型，認為螺紋（牙）主要受剪力，只校核切應力τ≤[τ]（[τ]為許用剪切應力）即可滿足螺紋設計要求。同時采用科學類比方法，發現內外螺紋受力等效于墊圈沖孔力學應力狀態，所以可以借用墊圈沖孔應力狀態來進行對比分析。

1? ? 材料力學定義懸臂梁結構要素

外螺紋、內螺紋強度校核都是延用Sopwith將螺紋展開看作懸臂梁結構進行的，即對彎曲正應力σω、剪應力τ、擠壓應力σP和修正系數k分別進行校核[1]：

σω

=≤[σω]，

τ=

≤[τ]，

σP=

≤[σP]，

k=0.55～0.75，

FS=

（1）

式中：FS為單個螺紋（牙）受力；F為螺紋副的軸向拉力；Z為旋合有效圈數；b為牙底圓周長（對于內螺紋，b=πD，D為內螺紋基本大徑；對于外螺紋，b=πd1）；k為考慮到各圈螺紋（牙）不均勻的系數；d1為外螺紋小徑；d2為外螺紋中徑；h為螺紋牙底厚度。

按材料力學[6]彎曲理論解析法得出，存在剪應力下的彎曲為橫力彎曲，橫力彎曲的剪應力為純剪應力的1.5倍，即：

τmax=? ? ? ? ? ? ? ? ? ? ? ?（2）

橫力彎曲是在純彎曲正應力計算的基礎上引入了兩個假設，一個是平面設計，另一個是認為縱向纖維面無應力。公式（1）（2）是針對梁截面高度（牙厚）遠小于跨度（牙高）的實際梁，這種梁才有可能滿足平面假設，才會與實際偏差非常小[7]。第二假設也是只有高度/跨度（牙厚/牙高）比值遠小于1，縱向正應力與彎曲正應力比值才非常小，才可以忽略不計縱向正應力[7]。

而螺紋（牙）恰恰相反，牙厚大于牙高，第二點假設懸臂梁是一端開口，一端固定，而真實的螺紋（牙）是環形閉合的，故公式（1）（2）與實際有出入。

用懸臂梁結構彎曲正應力和切應力假設計算得到的公式（1）（2）與實際有出入，所以用懸臂梁做假設校核強度是不精確的。為了滿足校核的要求，只有過大提高安全系數K來保證螺紋連接強度的安全性，這不利于挖掘螺紋工件材料、性能等潛能，也不能為螺紋失效分析提供可靠的理論依據。

2? ? 建立螺紋環形剪切力學模型

螺紋連接時外螺紋（牙）受到內螺紋（牙）壓力，可以假設壓力均勻分布在牙側面，均勻分布力為q，如圖2所示。FS（=qA）對外螺紋牙底圓周處會產生剪力和彎曲，剪力會引起切應力、彎曲會引起彎曲正應力，那螺紋斷裂是彎曲正應力σmax≥σb，還是τmax≥τb時引起的（σb為材料抗拉強度、τb為材料剪切強度）？下面來進行分析。

2.1? ? 螺紋斷口宏觀分析

試驗設計：螺栓在受拉力時，螺紋桿部受正應力，螺紋受彎曲正應力、切應力、擠壓應力。擠壓應力較小，一般不計[7]。

采用M6×20 GB/T 5783，HRC31～32，σb=1 070 MPa，性能滿足GB/T 3098.1—2010要求的螺栓來進行試驗。

為了讓螺栓桿部不斷裂，螺栓螺紋脫扣，螺母厚度設計小于0.6D，本次厚度H分別為1.5、2.0、2.5、3.0、3.5 mm，其余尺寸符合GB/T 6170—2015《1型六角螺母》標準要求，硬度為HRC23～26，機械性能滿足標準GB/T 3098.2—2015要求。

試驗方法：螺栓、螺母連接組合，模擬實際裝配受力方式，用扭矩安裝，如圖3所示。

試驗結果如表1所示。

在40倍投影儀上對斷裂件進行宏觀觀測，如圖4所示（螺母厚度H=3 mm），從斷口來看是剪斷的，若是彎曲過截斷裂的斷口，總體上來說特征與拉伸斷裂斷口相似，在彎曲斷口上可以觀察到明顯的放射線或人字花樣[8]。

當試樣受彎曲載荷作用時，凸面受拉應力分布與拉伸相似，斷裂部位存在塑性變形。斷口上一般可以看到三個特征區域：纖維區、放射區和剪唇。凹面受壓應力分布與單向壓縮近似，有中間腰鼓型，試樣中心應力為零。而實際螺紋（牙）斷口不是彎曲正應力造成的形貌，圖4未見放射線或人字花樣及三個特征區域，斷裂明顯是由切應力引起，斷面相對較為平滑，顏色較暗。

2.2? ? 剪切定義要素

由試驗中斷口分析得知，斷裂主要是剪斷的，剪切的特點如下：作用于構件某一截面兩側的力，大小相等，方向相反，且相互平行，使構件這一截面（剪切面）的兩部分發生相對錯動的變形。而連接件外螺紋小徑d1與內螺紋小徑D1理論值一樣，實際公差非常小，可以理解d1圓周處受大小相等、方向相反且相互平行的兩個力，如圖5所示，所以符合剪切定義要素。

3? ? 螺紋（牙）環形受剪力學模型切應力公式

3.1? ? 外螺紋受力形式類似于墊圈沖孔應力狀態

根據上面螺紋（牙）斷裂形態得出結論：螺紋（牙）是被剪斷的。根據試驗結果提出螺紋（牙）環形剪切力學模型假設。如圖5、圖6所示，螺母擰緊時，螺栓桿部受到均勻載荷q2，外螺紋受到均勻載荷q1，q1與q2方向相反。外螺紋與螺母內螺紋牙個數基本一一對應，每個螺栓螺紋（牙）都是環形結構，類似多個重疊圓形薄板，受力形式等效于墊圈沖孔力學狀態，如圖7所示。可用科學研究的類比法來分析：內螺紋（牙）類似多個凹模，螺栓桿部在螺母（或螺栓）旋擰時受拉，類似多個凸模，每個外螺紋桿部的類似凸模連續對應每個內螺紋凹模。由于內螺紋小徑D1與外螺紋小徑d1配合公差非常小，和沖孔原理一樣，都是圓周πd1處受彎受剪但主要受剪，最終是切應力τ造成金屬斷裂分離。

3.2? ? 螺紋小徑d1、D1與沖孔凹凸模單邊間隙比較

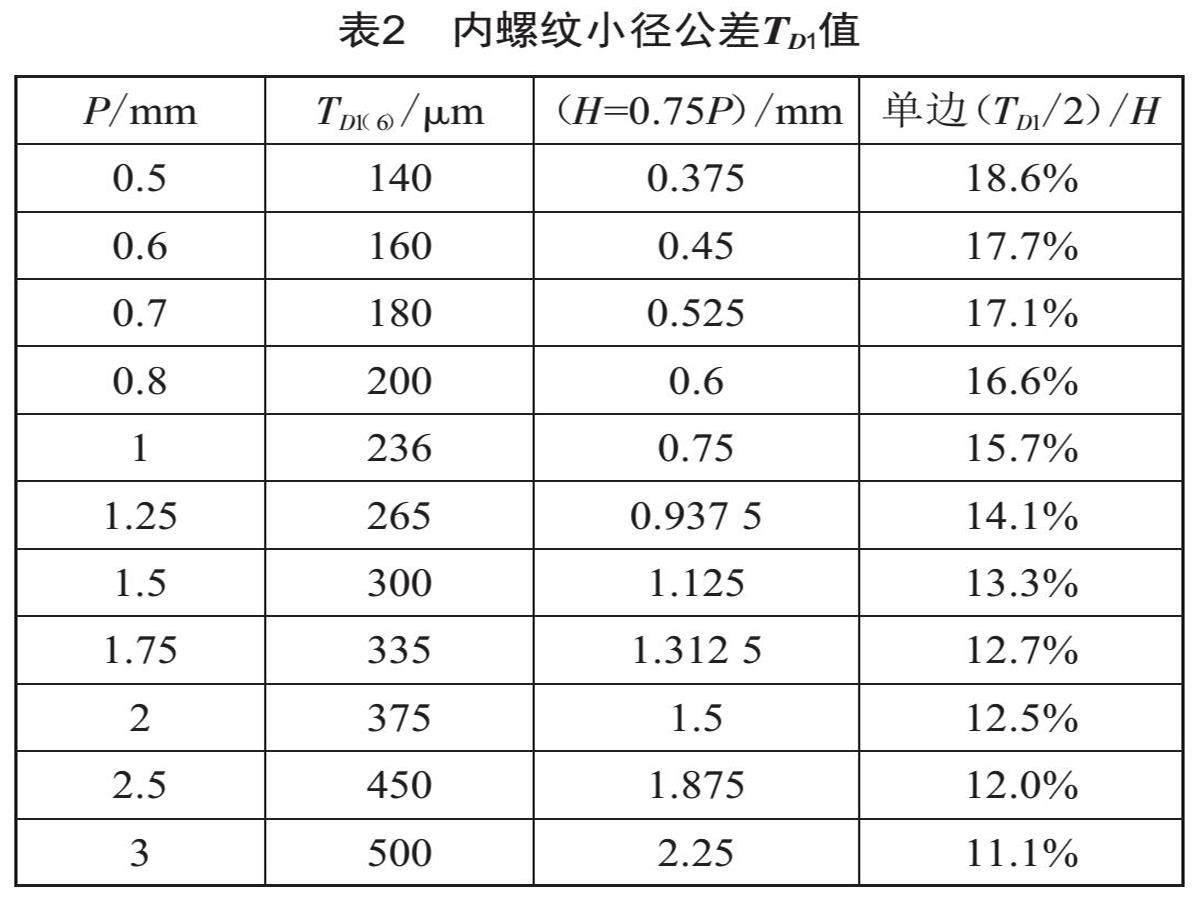
將外螺紋小徑d1與內螺紋小徑D1之間差值與墊圈沖孔凹凸模單邊間隙進行比較，內螺紋小徑D1按GB/T 197—2018《普通螺紋 公差》規定：當0.2 mm≤P≤0.8 mm時，TD1（6）=433P-190P1.22；當P≥1 mm時，TD1（6）=230P0.7。其中，（6）為6級精度，TD1的單位為微米，具體數據如表2所示。

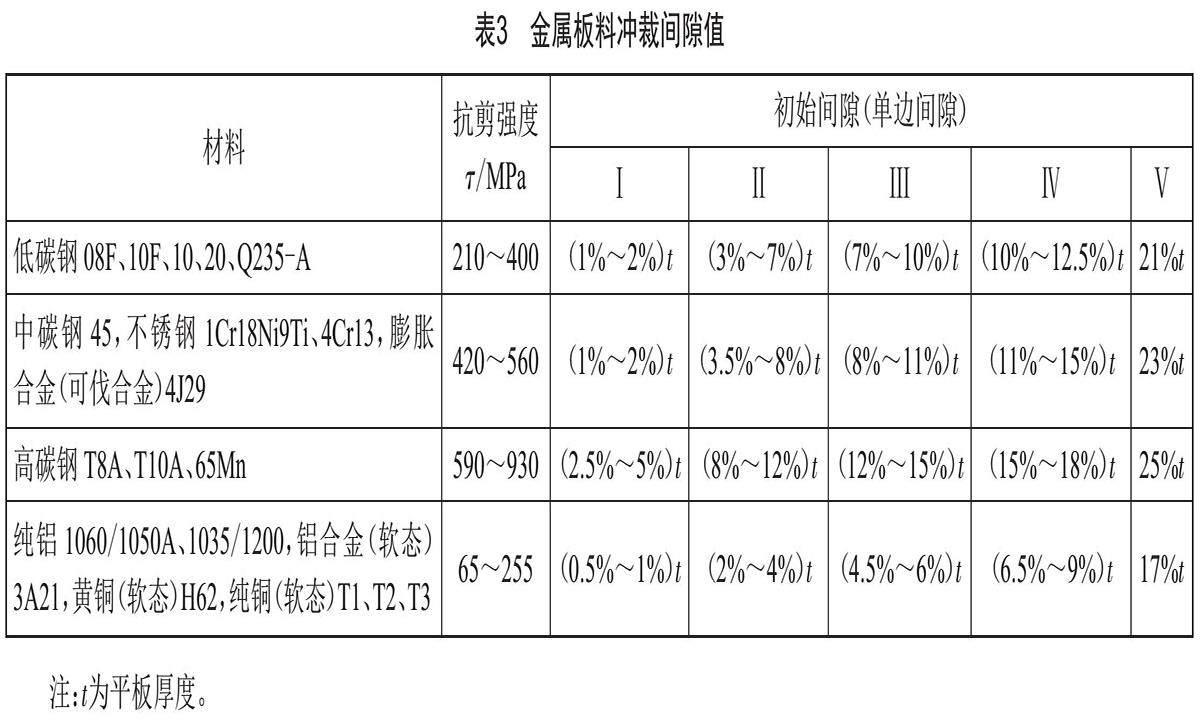
螺栓與螺母性能等級按GB/T 3098.2—2015搭配，螺母的性能級別與螺栓性能級別一樣，如8級螺母配8.8級螺栓，螺紋公差一般按GB197 6H/6h配合[9]。6H/6h公差間隙與根部厚度0.75P比值（表2）與GB/T 16743—2010《沖裁間隙》標準中金屬板料沖裁單邊間隙值（表3、圖7）進行比較，取墊圈τ在590～930 MPa這擋。

由表3可知，金屬板料沖裁單邊間隙值Ⅲ類（12%～15%）t、IV類（15%～18%）t。當P≤0.8 mm時內螺紋小徑D1與外螺紋小徑d1公差間隙處在Ⅳ類，當P≥1 mm處在Ⅲ類，都小于螺紋斷裂部位厚度h。外螺紋底部d1牙厚0.87P，即t=0.87P，完全與沖孔墊圈凹凸模單邊間隙一致。若板料要產生彎曲，凹凸模間隙必須滿足1.05t～1.15t[10]，而螺紋配合公差要求不滿足1.05τ～1.15τ條件，所以不可能彎曲斷裂。因此，科學類比法說明，配合安裝后螺栓與螺母受力狀態完全等效于沖孔墊圈受力狀態，可以借鑒沖孔墊圈受力狀態進行分析。

螺紋變形過程與沖孔墊圈受力過程一樣，由以下幾個過程組成：

1）彈性變形階段：變形區產生彈性壓縮、拉伸、彎曲等變形。

2）塑性變形階段：旋擰螺栓或螺母，螺栓桿部繼續受拉，螺紋（牙）切應力達到屈服極限，外螺紋在內螺紋作用下產生塑性剪切變形。

3）斷裂階段：螺栓桿部繼續受拉，外螺紋（牙）應力達到了剪切強度極限τb，在外螺紋根部d1圓周處產生微小裂紋。

在切應力作用下，裂紋不斷擴展，外螺紋（牙）從螺紋桿部分離，完成外螺紋被內螺紋剪切過程。

墊圈沖裁力計算公式[10-11]：

F=KAτb=1.3Ltτb? ? ? ? ? ? ? ? ? ? （3）

式中：F為沖裁力；K為系數，取1.3，主要考慮沖裁設備承載能力、材料性能的變化及設備沖裁速度快等因素；A為沖裁面積；τb為材料的抗剪切強度；L為沖裁斷面的周長；t為材料厚度（即沖裁件的厚度）。

而旋擰螺栓或螺母速度慢，K系數肯定小于1.3，具體多少？下面來推導。

3.3? ? 螺紋環形剪切力學模型K系數

假設剪切應力：

τmax=? ? ? ? ? ? ? ? （4）

式中：FS為單個螺紋等效集中力，與螺桿軸心平行；b為外螺紋小徑周長，b=πd1；h為外螺紋d1處牙高，h=0.87P。

根據材料力學第四強度理論，螺紋剪切應力與螺桿正應力滿足τmax≤[6]。螺母厚度遵循≥0.8D，螺紋有效長度遵循≥0.6D。

考慮到倒角及部分不全螺紋（牙）以及螺紋不均勻受力，螺紋有效長度取ZP=0.72D。

Z為螺栓與螺母嚙合圈數，希望當Z≥時，若過扭則螺桿應斷裂。根據上述已知條件，可以確定K值。現在來推導τ=、FS=、τ=及K值。

當K=？時，Z≥（D為內螺紋基本大徑，d為外螺紋基本大徑，數值相等，如圖2所示）的情況下才能在過扭時發生螺桿斷裂。

1）首先螺母內螺紋大徑剪切面積A母=Dπ×0.87P，而螺栓外螺紋根部小徑d1剪切面積A栓=d1π×0.87P，因為D>d1，所以A母>A栓，螺母與螺栓性能級別一樣，故只討論螺栓外螺紋受力情況。

2）切應力最大應滿足τ≤[6]=，

τ=；令τ=，=，=

；令A紋=（A紋為螺紋等效剪切應力面積），取Z=：

A紋==? ? ? ? ? ? ? （5）

從公式（5）可知：若A紋>A桿，首先螺桿受正應力產生塑性變形甚至斷裂；若A紋

3.4? ? 用數值逼近方法求出K值

因外螺紋、內螺母制造都存在公差，國家標準公差都應滿足A紋>A桿，按極限情況內螺紋小徑取最大值D1+TD1（TD1為內螺紋小徑公差值）、外螺紋取最小值d-Td（Td為外螺紋公差值）來推導K值。

按HB 6443—2008和GB/T 3098.1—2010得到d3=d1-=d-1.082 5P-0.144 3P=d-1.226 8P（H為螺紋原始三角形高度），且：

A桿=d32? ? ? ? ? ? ? ? ? ? （6）

式中：d3為GB/T 196—2003《普通螺紋 基本尺寸》中的螺栓最大小徑。

按GB/T 197—2018，外螺紋大徑6級公差為：

Td（6）=180P

-

μm? ? ? ? ?（7）

式中：P為螺距。

內螺紋小徑6級公差為：

TD1（6）=230P0.7 μm? ? ? ? ? ? ? ? ? （8）

當0.2 mm≤P≤0.8 mm時：

TD1（6）=（433P-190P1.22 ） μm? ? ? ? ? ? ? （9）

嚙合深度為：

X（極限情況）=? ? ? ? （10）

當內外螺紋公差處于極限時，公式（5）中b、h分別用bx=（d-2x）π、hx=0.125P+1.154 7X代入進行計算（圖2）。

若把式（7）（8）（9）Td、TD1代入式（10）計算X非常復雜，也沒有精確解。

現根據GB/T 197—2018具體數值求解。

選取1）d=6 mm，P=1 mm，d/P=6；2）d=12 mm，P=1.75 mm，d/P=6.857；3）d=20 mm，P=2.5 mm，d/P=

8；4）d=36 mm，P=4 mm，d/P=9。一般常用d/P都在6～9之間，這種選取具有普遍性。

根據上面分析，K取值范圍1.0～1.3。材料力學強度校核條件τmax≤[τ][6]（[τ]為材料許用切應力），只有K取最大值才能使切應力τ取最大值τmax。即τmax=，在b、h、Z、d符合螺紋標準的情況下，根據公式（5）（6），只有當Kmax取最大值時，A紋=。所以尋找最大K值，應使（A紋-A桿）/A桿為最小值，且同時滿足A紋-A桿≥0，才能滿足τmax≤要求。

根據公式（5）（6），A紋==d32=A桿，A紋=A桿，考慮到極限公差只有在K=1.2時A紋與A桿相對誤差最小，如表4所示。

螺母厚度≥0.8D、螺紋有效長度≥0.6D是國家標準規定的，且滿足實際要求，有大量數據支撐。通過表4知道只有K=1.2，A紋才最接近A桿；K=1.3，A紋-

A桿<0，不滿足A紋-A桿≥0要求，且相對誤差大，所以K取1.2滿足要求。

通過建立螺紋環形剪切力學模型最終確定力學模型公式：

τ==? ? ? ? ? ? ? ? （11）

其中，Z≥（外螺紋大徑d=內螺紋大徑D）。

4? ? 試驗驗證

具體采用不同的螺母厚度H進行試驗，當τ>τb==618 MPa，試驗數據如表1所示，螺紋剪斷如圖4所示（H=3 mm）。

A紋=≈16.9 mm2

A桿=d32=×4.772≈17.86 mm2

即A紋

當H=0.6D（有效螺紋長度約3.2 mm）時，A紋=

19.43 mm2。A紋>A桿，螺桿受拉應力斷裂，試驗結果證明公式（5）（11）是正確有效的。

假設內外螺紋間隙較大，未按6H/6h或6G/6h配合，則要求螺紋配合間隙應滿足：

≤hx? ? ? ? ? ? ? ? （12）

式中：D1實為內螺紋小徑實際值；hx為內螺紋D1實與外螺紋嚙合對應的外螺紋牙X的牙厚。

即：

0.541 25P-x≤hx=0.125P+1.154 7x? ? ? ?（13）

推導出應滿足x≥0.193P，即間隙≤hx滿足要求。

當FS一定時，D1（x）在x≥0.193P變動時，螺栓外螺紋與內螺紋在D1（x）嚙合圓圈處被剪切。進行試驗，結果如表5、圖8所示，從表5及圖8可知，外螺紋（牙）被剪斷而不是彎曲斷裂。

5? ? 螺紋（牙）環形受剪切力學模型理論的應用——自鎖螺母的發明

通過上面的分析及試驗驗證，有理由相信在螺紋連接圓周處是剪切危險截面，校核切應力τ≤[τ]就可以了，沒必要校核彎曲應力、擠壓應力，不能用彎曲應力基本公式σω=來進行校核。

通過上面分析知道，外螺紋剪切危險截面在d1圓周處，即：

τ==，Z≥? ? ? ?（14）

根據上面分析結果A紋=，K=1.2，A紋=，其中A紋為螺紋剪切等效應力面積。

當A紋>A桿（A桿=d32）時，螺桿斷裂；當A紋

6? ? 結論

1）把螺紋（牙）展開視為懸臂梁，按懸臂梁進行強度校核，缺乏嚴密的理論依據和試驗結果支撐。

2）以試驗結果為依據，同時采用科學類比法，以內螺紋小徑D1與外螺紋小徑d1之間的公差間隙，對比沖裁平墊圈凹凸模單邊間隙，由數據得出內螺紋與外螺紋配合連接受剪力狀態等效墊圈沖孔受剪狀態，即當A紋

3）通過試驗以及類比法，提出了螺紋（牙）環形受剪力學模型假設。依據假設推導出螺紋受剪切應力公式：τx=，若dx=d1，則hx=0.87P，τ=，用τ<[τ]進行剪切強度校核即可，不再進行彎曲強度、擠壓強度校核，不再提高K系數或降低[τ]許用應力來校核。這樣可以提高材料的潛能，并保證內外螺紋連接可靠性。

4）依據螺紋（牙）環形受剪力學模型假設，推導出當過擰時，是螺栓（螺釘、螺柱等）桿部斷裂還是外螺紋被剪斷判決不等式：A紋?A桿。一般希望在過扭時出現桿部斷裂而不是脫扣，因為桿部斷裂容易發現，而脫扣是緩慢的，不容易發現，會帶來安全隱患，不等式提供了理論設計依據。

5）依據不等式A紋?A桿，設計制造了內螺紋厚度H≤0.5D的自鎖螺母，其原理為：外螺紋（牙）被剪斷，其金屬填塞至內螺紋牙槽內，破壞了螺紋旋進或退出路徑，達到了不松動自鎖目的。

[參考文獻]

[1] 《緊固件連接設計手冊》編寫委員會.緊固件連接設計手冊[M].北京：國防工業出版社，1990.

[2] 陳巖，蘆旭，江鵬，等.影響螺紋副軸向力分布均勻性的關鍵因素分析[J].東北大學學報（自然科學版），2017，38（8）：1142-1147.

[3] 陳海平，曾攀，方剛，等.螺紋副承載的分布規律[J].機械工程學報，2010，46（9）：171-178.

[4] 左永強，樊春明，惠坤亮，等.螺紋牙強度校核有限元仿真方法探討[J].機械工程師，2019（7）：124-125.

[5] 李俊巖，包婷萍，侯鵬飛，等.基于有限元分析的螺紋連接強度設計技術研究[J].導彈與航天運載技術，2020（2）：78-82.

[6] 劉鴻文.材料力學Ⅰ[M].6版.北京：高等教育出版社，2017.

[7] 徐芝綸.彈性力學[M].5版.北京：高等教育出版社，2016.

[8] 王榮.失效機理分析與對策[M].北京：機械工業出版社，2020.

[9] 王三民.現代機械設計手冊：連接件與緊固件[M].北京：化學工業出版社，2020.

[10] 肖景容，姜奎華.沖壓工藝學[M].北京：機械工業出版社，2011.

[11] 田光輝.模具設計與制造[M].3版.北京：北京大學出版社，2021.

[12] 彭展里.一種基于強度關系的內螺紋小徑力學模型建立方法：CN116522528A[P].2023-08-01.

[13] 彭展里.一種螺母自鎖方法及其自鎖結構：CN116044883A[P].2023-05-02.

收稿日期：2024-01-17

作者簡介：彭展里（1957—），男，江西南昌人，研究員級高級工程師，從事螺紋連接件設計、工藝研究及故障分析工作。