基于國際平整度指數IRI的計算系統
趙杜元 許偉強


收稿日期:2024-04-01
作者簡介:趙杜元(1986—),男,本科,工程師,研究方向:公路檢測。
摘要 平整度作為公路交竣工驗收和路面技術狀況檢測的重要指標,深入認識其檢測原理和四分之一車模型理論是提高平整度檢測精度的重要舉措。文章從四分之一車模型出發,介紹了其振動微分方程和四個變量的遞歸方程,采用python語言開發了基于國際平整度指數IRI的計算系統,并與“多功能路況快速檢測系統(CiCS)”的IRI測值進行比對驗證,相關系數為0.93,相關性較高,驗證了該計算系統IRI計算值的高準確性和高相關性。
關鍵詞 國際平整度指數IRI;計算系統;四分之一車模型
中圖分類號 U416.2文獻標識碼 A文章編號 2096-8949(2024)11-0027-03
0 引言
車載式激光平整度儀以其檢測高效率和高精度的優點,已在新建公路交竣工驗收和在役公路路面技術狀況檢測中得到了大規模應用,并且其檢測對象已從過去的以國省干線公路為主,拓展到現在的大規模農村公路路況檢測中[1]。車載式激光平整度儀屬于縱斷面平整度測試系統,其通過測量路面縱向斷面高程值以直接計算出國際平整度指數IRI來表征路面平整度。
國際平整度指數IRI(International Roughness Index)是世界銀行推薦使用的標準的平整度測試指標。由于所關注的影響行車特性的路面波長范圍不同、平整度的計算方法不同,即使是同類型的平整度測試設備,各種平整度指標也難以進行橫向比較,所以美國、英國、巴西等國于1982年開始以在巴西進行的3年國際道路平整度試驗(IRRE)為基礎發布了46號報告,該報告中采用了1/4車模型發表了IRI標準計算程序,該46號報告旨在針對不同國家、不同平整度檢測設備、不同評價指標,建立其與國際平整度指數的相關關系。
IRI是一個斷面類的數學統計指標,具有時間穩定性,易于重現,對路面1.2~30.5 m范圍內的波長有較好的頻率響應特征,與大多數平整度測試結果有良好的相關性關系,以IRI為標準的平整度測試指標,使不同平整度測試系統的結果可以相互比較[2]。
1 IRI模型
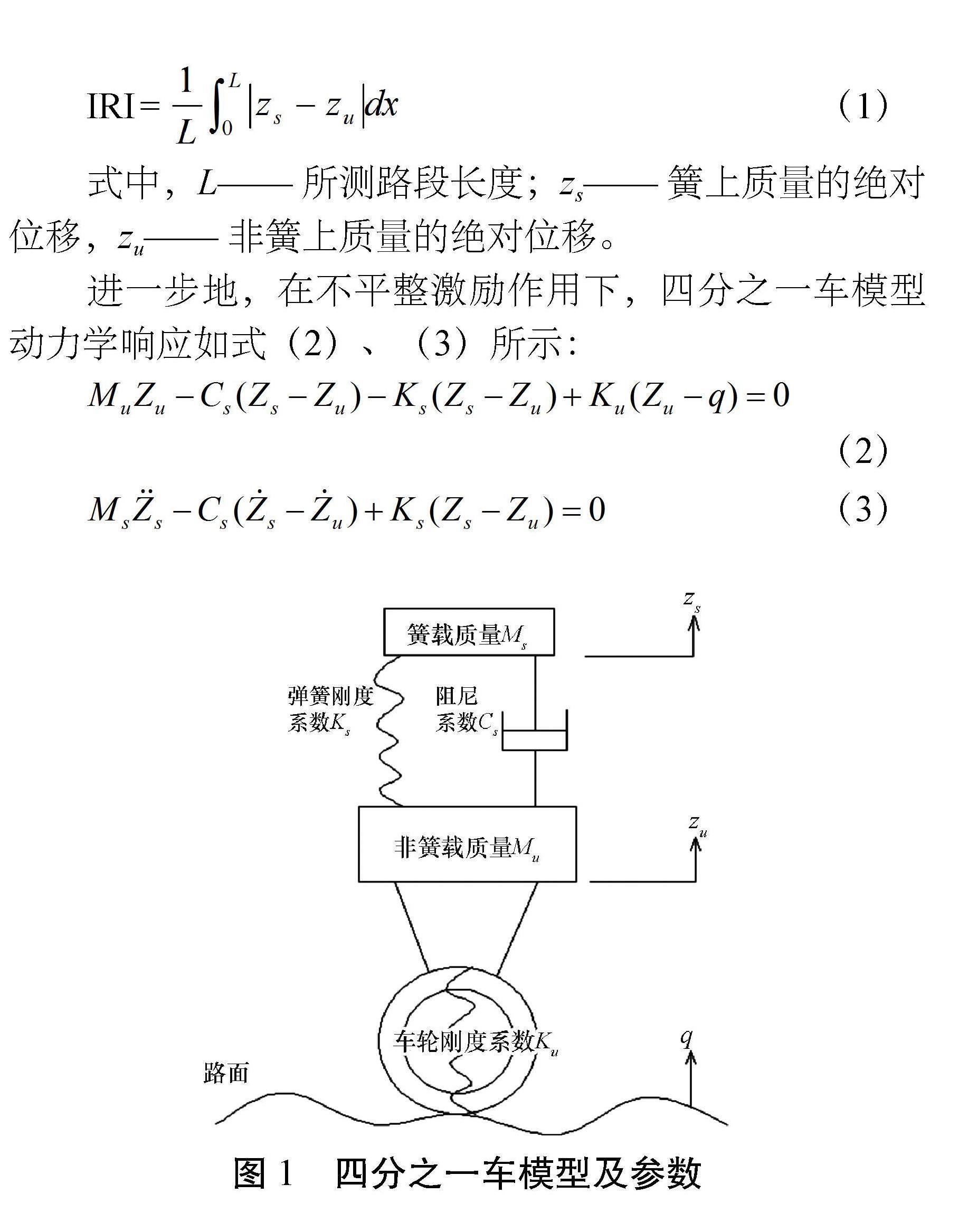
國際平整度指數IRI采用四分之一車模型[3],以80 km/h速度穩定行駛,通過斷面高程數據經過數學建模計算獲得,如圖1所示,非彈載質量代表了車輛減震器下部的底盤構件,彈載質量代表了減震器上部的車輛構件。
根據世界銀行定義,IRI值為單位距離內簧載質量和非簧載質量的相對位移累計值,由式(1)計算:
IRI (1)
式中,L——所測路段長度;zs——簧上質量的絕對位移,zu——非簧上質量的絕對位移。
進一步地,在不平整激勵作用下,四分之一車模型動力學響應如式(2)、(3)所示:
(2)
(3)
圖1 四分之一車模型及參數
振動微分方程(2)、(3)描述了標準車模型在不平整激勵下的動力學響應,在實際工作中通常采用數值迭代計算的方法求解IRI值,世界銀行即提出狀態轉移矩陣法計算。
令z1和z2分別代表簧載質量的速度和加速度,z3和z4分別代表非簧載質量的速度和加速度,在前一位置的4個變量z1'、z2'、z3'、z4'已知的情況下,且與下一位置間縱坡度y'計算求得的情況下,則下一位置處的4個變量z1、z2、z3、z4可以利用遞歸方程計算得到:
(4)
其中,當采樣間距為0.25 m時,式(4)的系數矩陣為:
當采樣間距為0.1 m時,式(4)的系數矩陣為:
轉移矩陣
4個變量z1'、z2'、z3'、z4'的初始值應用前11 m的平均坡度:
(5)
式中,y11——第11米處的高程值;y0——檢測起點處的高程值。
從第2點至第n點可以迭代求解遞歸方程(4),如計算4個變量z1、z2、z3、z4值,則由式(1),IRI計算公式變為。
由上述可知,因為四分之一車模型的標準條件是在大量現場試驗中將相關參數進行調整擬合,使得IRI與反應類設備的測值具有非常好的相關性,解決了各個不同的平整度測試設備間的一致性問題。同時,IRI考慮了絕大多數車輛的反應特性,可以描述引起車輛振動的縱斷面高程變化,且IRI只與斷面高程相關,采樣間隔的變化對計算結果的影響較小[4]。
2 系統開發及驗證
基于國際平整度指數IRI的計算系統是在Windows
10開發環境下,采用 python 語言,主要使用PyQT5.15.4、
Pycharm2023等工具進行開發,如圖2所示。
該軟件由登錄模塊、數據導入模塊、計算模塊、導出模塊組成。該軟件根據一定采樣頻率的路面相對高程數據,基于世界銀行46號文件實現路面國際平整度指數IRI的計算功能。
為了驗證該系統IRI計算值的準確性,采用目前國內主流的車載式激光平整度儀“多功能路況快速檢測系統(CiCS)”于成都市在建項目天邛高速公路進行路面平整度現場檢測,檢測位置為主車道K14+879~K18+889,CiCS系統沿公路縱向每間隔100 mm采集路面高程值,據此計算10 m長度范圍內的402個點的IRI中公高科值;該系統采用CiCS系統采集的路面高程值,并據此計算10 m長度范圍內的402個點的IRI四川華騰值,前20點的數據如表1所示。
如表2所示,IRI中公高科與IRI四川華騰計算數值在平均值、標準差、最小值、最大值四個維度上較為接近;如圖3所示,IRI中公高科與IRI四川華騰計算數值的相關性較好,相關系數為0.93。如圖4~5所示,IRI中公高科與IRI四川華騰計算數值按照檢測樁號的趨勢性分布較好,該計算系統取得了較高的測試精度。
圖2 基于國際平整度指數IRI的計算系統界面
表1 前20點的高程檢測及IRI計算數據表
測點
序號 CiCS高程檢測數據 IRI計算
脈沖 樁號/m 高程/
0.1 mm 車速/
(cm/s) 中公
高科 四川
華騰
1 20 702 18 889 136.17 323 1.18 1.15
2 30 376 18 879 141.36 310 0.63 0.61
3 40 050 18 869 144.23 409 1.12 1.02
4 49 724 18 859 129.34 451 1.19 1.21
5 59 398 18 849 140.8 431 0.99 0.9
6 69 072 18 839 156.97 409 0.62 0.78
7 78 746 18 829 158.44 456 0.64 0.68
8 88 420 18 819 162.93 483 0.60 0.6
9 98 094 18 809 137.76 495 0.84 0.85
10 107 768 18 799 138.74 501 0.63 0.6
11 117 442 18 789 155.07 504 1.18 1.14
12 127 116 18 779 144.99 504 0.56 0.68
13 136 790 18 769 160.81 501 0.52 0.49
14 146 464 18 759 166.3 495 1.70 1.53
15 156 138 18 749 149.35 489 0.68 0.87
16 165 812 18 739 159.5 483 0.55 0.52
17 175 486 18 729 148.01 483 0.81 0.73
18 185 160 18 719 158.36 511 1.26 1.35
19 194 834 18 709 134.03 489 0.68 0.71
20 204 508 18 699 147.2 466 0.63 0.58
表2 IRI計算信息對比表
IRI_10 m/(m/km) 點數 平均值 標準差 最小值 最大值
IRI四川華騰 402 0.71 0.29 0.27 3.39
IRI中公高科 402 0.72 0.28 0.28 3.32
3 結論
該文介紹了國際平整度指數IRI的四分之一車模型理論,然后采用 python 語言開發了基于國際平整度指數IRI的計算系統,采用主流的車載式激光平整度儀“多功能路況快速檢測系統(CiCS)”所采集路面高程值計算所得的IRI中公高科與IRI四川華騰進行比對,兩計算數值在平均值、標準差、最小值、最大值四個維度上較為接近,相關系數為0.93,相關性較好,且按照檢測樁號的趨勢性分布較好,驗證了該計算系統IRI計算值的高準確性和高相關性,對于大規模路況檢測起到了巨大的技術支撐作用。
參考文獻
[1]趙杜元, 許偉強, 趙泓博. 基于多功能路況快速檢測系統(CiCS)的彎道比對試驗[J]. 工程建設標準化, 2023
(8): 365-366.
[2]公路路基路面現場測試規程: JTG 3450—2019[S]. 北京:人民交通出版股份有限公司, 2019.
[3]車載式路面激光平整度儀: JT/T 676—2009[S]. 北京:人民交通出版社, 2009.
[4]常成利. 國際平整度指數量值溯源與傳遞技術研究[D]. 北京:北京工業大學, 2011.

