基于PH-GAT的精分患者分類預測模型研究

盛志林 陰桂梅 符永燦

收稿日期：2023-09-19

DOI：10.19850/j.cnki.2096-4706.2024.07.023

摘? 要：對目前基于腦網絡的分析進行研究，研究顯示，分析方法大致分為基于持續同調方法的分析和基于深度學習模型的分析。為了提高腦疾病診斷的預測能力，模型將持續同調集成到GAT模型中，使其具有“拓撲意識”。在模型的最后使用LSTM模型，目的是為了捕捉到所形成特征中的時序信息，從而提高分類預測的效果。在PH-GAT模型下，采用局部和全局的融合特征對Theta頻段數據分類，分類準確率高達0.930 9。如此不僅可以發現早期診斷精神分裂癥的客觀、有效的影像學標志物，還可以提高腦疾病診斷的預測能力。

關鍵詞：腦網絡；持續同調；圖注意力網絡；精神分裂癥

中圖分類號：TP391；TP183? 文獻標識碼：A? 文章編號：2096-4706（2024）07-0107-07

Research on a Classification Prediction Model for Schizophrenic Patients Based on PH-GAT

SHENG Zhilin， YIN Guimei， FU Yongcan

（College of Computer Science and Technology， Taiyuan Normal University， Jinzhong? 030619， China）

Abstract： This paper studies the current analysis based on cerebral network， the study shows that the analysis methods can be broadly categorized into two main approaches： analysis based on continuous homotopy methods and analysis based on Deep Learning models. In order to enhance the predictive capabilities of brain disease diagnosis， this model incorporates continuous homotopy into the GAT model， endowing it with a “topological awareness”. Towards the end of the model， the Long Short-Term Memory （LSTM） model is employed to capture temporal information embedded within the extracted features， thereby enhancing the effectiveness of classification prediction. Under the PH-GAT model， a fusion of local and global features is applied for classifying data in the Theta frequency range， achieving a high classification accuracy of 0.930 9. This approach not only enables the discovery of objective and effective imaging biomarkers for early schizophrenia diagnosis， but also enhances the predictive capabilities of brain disease diagnosis.

Keywords： cerebral network; continuous homotopy; Graph Attention Network; schizophrenia

0? 引? 言

腦信號數據作為一種重要的生物信號數據，對于理解大腦活動和認知過程具有關鍵意義。近年來，隨著神經科學和計算神經學領域的快速發展，圖神經網絡（Graph Neural Networks， GNN）[1]和循環神經網絡（Recurrent Neural Networks， RNN）[2]等深度學習模型在腦電信號數據處理中引起了廣泛的關注。在本論文中，我們將著重研究腦電信號數據分析中的關鍵方法，包括Graph Attention Network（GAT）、Graph Convolutional Network（GCN）、Long Short-Term Memory（LSTM）以及基于持續同調的拓撲數據分析[3]。我們將探索這些方法在腦電信號數據處理中的應用，并期望能夠為腦科學領域的研究和臨床實踐提供新的洞見和方法。

首先，GAT和GCN是兩種重要的圖神經網絡模型，它們被廣泛應用于圖數據建模。在我們的研究中，我們將利用GAT和GCN來構建腦電信號數據的圖結構，并通過自適應地學習節點之間的注意力權重和關系，更好地捕捉大腦區域之間的功能連接和信息傳遞。

其次，LSTM作為一種常用的循環神經網絡，其在序列數據建模中表現出色。在本論文中，我們將探索LSTM在腦電信號數據中的應用，特別是對于時間序列數據的特征提取和長期依賴關系建模。通過LSTM的應用，我們期望能夠更好地理解腦電信號數據中復雜的時間動態變化。

除了深度學習模型，我們還將研究基于持續同調的拓撲數據分析方法在腦電信號數據處理中的應用。拓撲數據分析是一種新興的數學工具，能夠捕捉數據的拓撲結構和形狀信息。我們將探索如何將這種方法應用于腦電信號數據，以揭示腦網絡的拓撲特征和拓撲動力學過程，從而更深入地理解腦的復雜活動。

綜上所述，本論文將綜合運用GAT、GCN、LSTM和基于持續同調的拓撲數據分析等多種方法，以探索腦電信號數據的深層特征和動態特性。通過這些研究工作，我們希望能夠為神經科學和腦科學領域提供新的分析手段和認知機制的理解，為相關疾病的診斷和治療提供有力的支持。

1? 基本原理

1.1? 圖注意力網絡

GAT [4]是一種基于圖神經網絡的模型，用于處理圖結構數據。GAT通過引入注意力機制，使得每個節點能夠自動學習不同節點之間的重要性，從而實現對圖數據的特征學習和節點分類任務。

GAT的核心創新點在于注意力權重的計算。對于每個節點，GAT使用可學習的參數矩陣和注意力權重向量來計算與其鄰居節點之間的注意力權重。注意力權重表示了節點之間的重要性，使得網絡能夠更關注對分類等任務更有貢獻的鄰居節點。注意力系數為：

（1）

為了計算注意力權重，GAT使用了LeakyReLU激活函數和Softmax歸一化：

（2）

通過對鄰居節點的特征加權求和，每個節點得到更新后的特征表示。GAT通常使用多頭注意力機制來增強模型表達能力，最后將多個頭的結果進行拼接或平均得到最終的節點表示。綜合式（1）和（2），整理到一起可得到完整的注意力機制：

（3）

GAT模型具有很強的表達能力，并在圖數據相關任務中具備出色的性能。它在社交網絡、蛋白質相互作用網絡以及腦電信號數據等領域都得到了廣泛的應用。

1.2? 圖卷積神經網絡

GCN [5]是一種圖神經網絡模型，用于處理圖結構數據。GCN通過卷積操作在圖數據上進行信息傳播和特征學習，使得每個節點能夠聚合其鄰居節點的信息，從而實現對圖數據的特征學習和節點分類等任務。

GCN的核心思想是基于圖卷積操作。對于一個包含N個節點的圖，GCN引入了可學習的參數矩陣來對節點的特征進行線性變換。通過對鄰居節點特征的加權求和，每個節點得到更新后的特征表示。GCN的圖卷積操作可以表示為以下算式：

（4）

其中 ，I是單位矩陣， 是? 的度矩陣（Degree Matrix），H是每一層的特征，σ是非線性激活函數。

通過多層的圖卷積操作，使得每個節點能夠聚合更廣泛的鄰居節點信息，從而實現對節點特征的層級化表示和復雜關系的學習，層特征傳播算式為：

（5）

最終，GCN可以通過節點特征向量進行節點分類、鏈接預測和圖表示學習等任務。但是GCN無法允許為鄰居中的不同節點指定不同的權重。

1.3? 長短期記憶網絡

長短期記憶網絡（LSTM）是一種特殊的循環神經網絡（RNN）[6]，專門用于處理具有時間依賴性的時序數據，如腦電信號等。LSTM具有優秀的記憶能力，能夠捕捉時序數據中的長期依賴關系，同時有效地解決傳統RNN中的梯度消失和梯度爆炸問題。

LSTM的基本單元是一個包含輸入門（Input Gate）、遺忘門（Forget Gate）、輸出門（Output Gate）和細胞狀態（Cell State）的結構。通過這些門控制機制，LSTM可以選擇性地記憶和遺忘過去的信息，并更新當前的狀態，其中遺忘門的形式方程為：

（6）

輸入門的形式方程為：

（7）

（8）

以及t時刻的Cell狀態（長時）方程為：

（9）

輸出門的形式方程為：

（10）

（11）

LSTM通過這種門控制機制，可以學習長期依賴的時序模式，對于處理時序腦電信號等數據具有良好的效果。

1.4? 持續同調

從原始數據中構建一個復形，復形是一種包含頂點、邊、三角形等元素的結構，用于近似表示原始數據的拓撲特征。從復形中生成對應的單純復形（Simplicial Complex）。單純復形是一種由單純形構成的拓撲結構，單純形是一種幾何元素，可以是點、線、三角形等的組合。這些單純形滿足一定的規則，比如邊必須連接兩個點，面必須由三條邊組成等，如圖1所示。

圖1? 不同維度單純復形示例

對于單純復形，我們可以計算持續同調（Persistent Homology， PH）。這一步的核心是計算不同維度的同調群（Homology Group）。同調群反映了復形中連通組件和空洞的性質。通過繪制持續同調圖（Persistence Diagram）或持續同調圖像（Persistence Image），我們可以直觀地展示數據中的拓撲特征在不同尺度上的持續性。PH的思想是，真正的拓撲結構在不同尺度下都會存在，而噪聲或隨機性的影響往往只在特定尺度范圍內出現，因此持續同調能夠幫助我們過濾掉噪聲，提取出數據中的穩定拓撲特征。

1.5? 構建鄰接矩陣

皮爾遜相關系數（Pearson Correlation Coefficient， PCC）[7]用于度量兩個信號之間的線性相關程度，PCC定義為兩變量之間的協方差和標準差的商，如式（12）所示：

（12）

2? 基于PH-GAT的精分患者分類預測模型

在本模型中，采用拓撲數據分析工具來提取隱藏在腦網絡復雜結構中的基本信息。持續同調（PH）[8]是拓撲數據分析中的一種數學工具，能夠提取穩定的拓撲特征。采用自適應腦網絡作為鄰接矩陣，選擇多個重要性特征進行拼接形成局部特征，再根據鄰接矩陣和其對應的局部特征進行圖卷積神經網絡特征學習，最后可以獲取到圖編碼特征全局表示。

將形成的基于圖論的腦網絡局部特征[9]、時頻域特征[10]拼接作為新的特征矩陣輸入到我們所搭建的GAT模塊中，利用GAT對局部特征進行多頭注意力分配節點權重值；再利用搭建的GCN模塊進行深度圖拓撲特征學習。隨后，將深度圖拓撲特征、圖編碼特征和高維拓撲特征[11]進行多尺度，多模態融合形成全局特征表示，最后將融合后的全局特征表示輸入時序模型LSTM對樣本進行分類預測。

在圖學習階段，提出了一個新的基于PH的圖注意力網絡模型PH-GAT，使用圖注意力層來學習節點表示，并使用一個可學習權重的注意力池層來獲得用于腦功能網絡分類的圖表示，所采用的池化方法使用可學習的參數，以單一的可學習標準從每個節點的表示中總結出圖的表示。使用LSTM模塊對所融合的時序信號特征進行分類預測，目的是為了捕捉到所形成特征中的時序信息，從而提高分類預測的效果。基于PH-GAT的精分患者分類預測模型如圖2所示。

2.1? 實驗數據

實驗采用北京回龍觀醫院103個首發精分病人和92個健康被試在閉眼靜息狀態下采集的59通道EEG數據。通過性別、年齡、受教育程度做匹配，兩組被試的人口統計學、PANNS分數等臨床數據統計信息如表1所示。

2.2? 實驗數據預處理

實驗使用Python的MNE工具包對EEG信號數據做預處理。將信號過濾為Delta（1～3 Hz）、Theta（4～7 Hz）、Alpha（8～12 Hz），Beta（13～

30 Hz）、Gamma（31～49 Hz）五個頻段。

每個樣本數據時間長均為230 s左右，利用滑動窗口[12]截取40～200 s的數據，每個樣本只截取160 s的數據信號長度。原因是在信號采集的開始或者結束時期，被試會由于注意力不集中導致信號數據出現偏差，對實驗結果略有影響。再針對160 s的信號數據，利用滑動窗口，使得一個被試的數據樣本被分為16個數據樣本，每個數據樣本的信號長度為10 s。

2.3? 構建腦網絡與VR復形

實驗使用Python中的Giotto-TDA拓撲機器學習工具箱構建腦網絡[13]和VR復形。模型中，VR過濾的最大閾值不設為固定值，通過動態判斷腦網絡的VR復形數不再發生變化結束構建腦網絡與VR過濾。使用PD對VR過濾得到拓撲特征進行可視化表示，如圖3為首發精分病人和健康被試在Beta頻段的PD。

2.4? 提取特征

對腦電信號數據提取相應的時域和頻域特征分別計算了平均絕對值、方差等時域特征[14]；對于每個樣本的腦電信號，可以使用快速傅里葉變換（FFT）將信號從時域轉換到頻域，可以得到頻譜信息，對于每個頻率分量，計算其功率譜密度，即信號在該頻率范圍內的能量或強度。這里提取平均功率譜密度等頻域特征。

提取腦網絡的局部特征作為EEG信號的節點特征，對于腦網絡的局部特征，計算度、介數、聚類系數和局部效率[15]，參照目前相關的研究成果，實驗選擇20%～40%的稀疏度范圍（步長為2%）[16]，計算了局部特征曲線下面積（Area Under the Curve， AUC），將局部特征值在稀疏度范圍內的AUC值作為每個節點的特征形成節點特征矩陣，提取節點特征并構成圖結構的過程如圖4所示。

對高維拓撲特征進行研究設計的過程中，由于VR濾流得到的持續圖PD并不能直接進入機器學習算法中進行分類，所以，基于拓撲數據分析的現有方法，我們將持續圖PD轉換為持續景觀圖PL，貝蒂曲線BE，熱核圖HE，這三種圖能從不同的維度觀察獲得的持續圖PD的特點。相對于直接從復雜的腦電時間數據中提取特征進行分類，從持續圖PD中提取拓撲特征具有極高的可解釋性與可視化性。為了高度概況獲得的三種拓撲特征圖，我們使用矩陣范數（1范數與2范數）對PL、BE、HE進行總結，在VR復形的每一維獲取一個矩陣范數，從而獲得可用于機器學習分類的特征數值，過程如圖5所示。

另外，VR濾流構造中的信息變化也是一個重要的拓撲特征表示方式，所以我們計算了拓撲圖的持續熵。然后對特征公式進行推理描述、并對特征表現形式與實現方式的問題進行研究討論并證明其有效性，表2為實驗所用拓撲特征及對應參數的選擇。

表2? 拓撲特征參數選擇

3? 實驗結果及分析

本文研究的實驗硬件環境為Intel Core i7 10870H CPU @ 2.20 GHz 2.21 GHz，內存為16 GB，軟件環境為64位windows 10，PyCharm Professional Edition 2021。

實驗分為兩個部分，第一部分是分別在五個頻段的數據下比較每個頻段的數據，單一的局部特征或是全局特征和融合后的特征在多個模型中分類準確率的表現。分別比較了GCN、GAT、LSTM、PH-GAT四個模型在局部特征、全局特征下的分類準確率，其中無論是在局部特征上的表現還是全局特征下的表現，都是PH-GAT模型效果最佳，分類效果如表3所示。

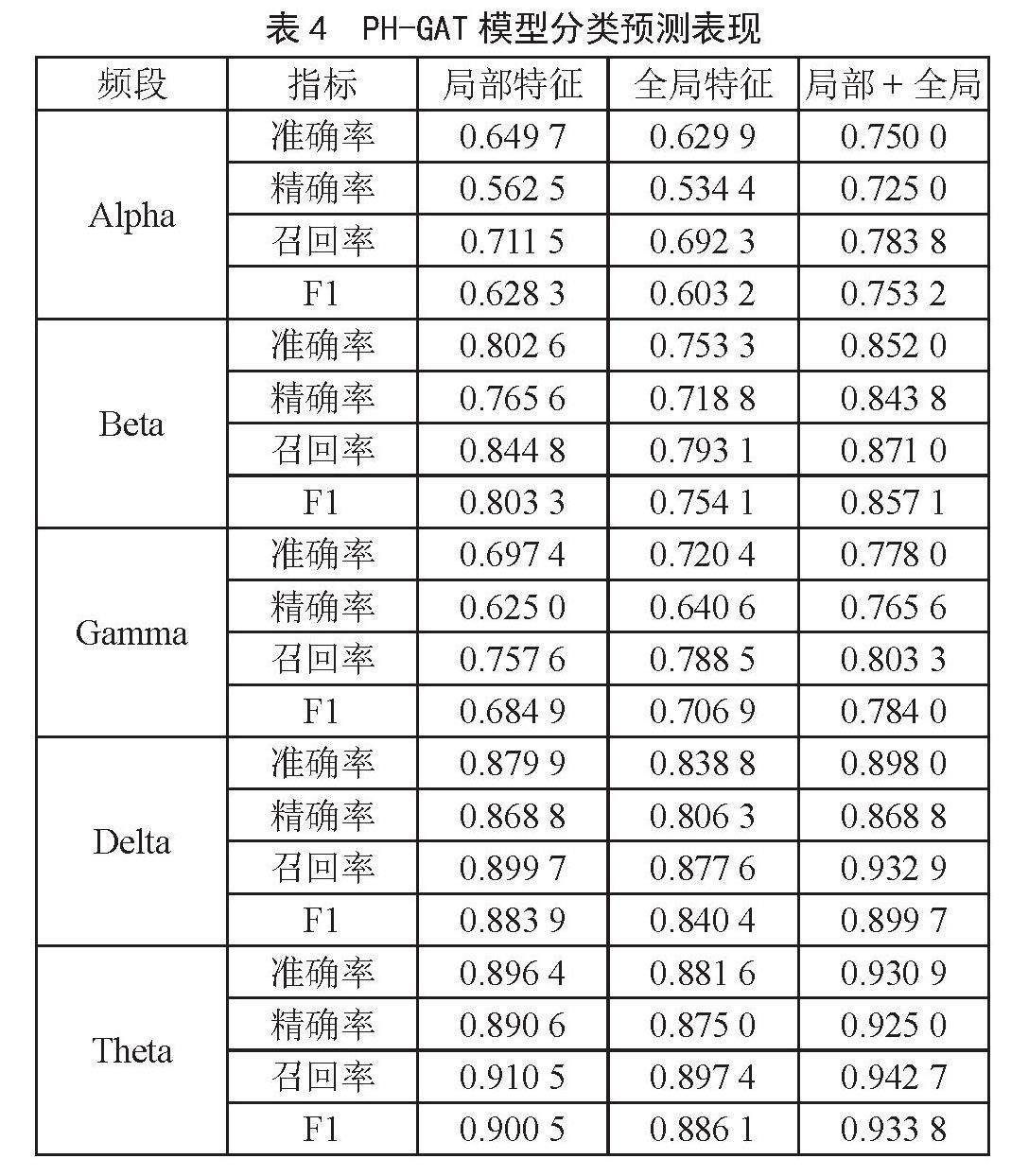
第二部分是比較了在PH-GAT模型下，分別提取局部特征、全局特征以及局部加全局的融合特征對五個頻段腦電數據的分類效果。通過比較精確率、準確率、召回率以及F1分數可以得知，在PH-GAT模型下利用局部加全局的融合特征對數據進行分類的效果最佳，具體的分類預測表現如表4所示。

4? 結? 論

綜上所述，在PH-GAT模型下，采用局部和全局的融合特征對數據的分類效果最佳，Theta頻段分類準確率高達0.930 9。這是由于采用了GAT和GCN等圖神經網絡模型，這些模型能夠捕獲腦電信號之間的復雜關系和拓撲結構，從而實現對多通道腦電數據的全局建模和特征學習。為了捕獲腦電信號數據的時空動態性，我們引入了長短期記憶網絡LSTM，該模型能夠有效地建模腦電信號數據的時序特征，從而更好地揭示大腦的動態過程。除此之外，還將持續同調方法應用于腦電信號數據處理中，通過構建腦電數據的持續同調圖，揭示了腦電數據的拓撲結構和拓撲特征，從而為大腦功能的拓撲學理解提供了新的視角。

本研究的綜合性方法可以為腦電信號數據處理領域的進一步研究和應用提供新的思路和方法。在未來，我們期待這些方法能夠被廣泛應用于腦機接口、神經科學、腦疾病的早期診斷以及腦功能的深入理解，為改善人類生活和健康貢獻一份力量。

參考文獻：

[1] 李路寶，陳田，任福繼，等.基于圖神經網絡和注意力的雙模態情感識別方法 [J].計算機應用，2023，43（3）：700-705.

[2] ROY S，KIRAL-KORNEK I，HARRER S. ChronoNet： A Deep Recurrent Neural Network for Abnormal EEG Identification [J/OL].arXiv：1802.00308 [eess.SP].（2018-01-30）.https：//arxiv.org/abs/1802.00308.

[3] STOLZ B J，EMERSON T，NAHKURI S，et al. Topological Data Analysis of Task-based fMRI Data from Experiments on Schizophrenia [J/OL].arXiv：1809.08504 [q-bio.QM].（2018-09-22）.https：//arxiv.org/abs/1809.08504.

[4] VELI?KOVI? P，CUCURULL G，CASANOVA A，et al. Graph Attention Networks [J/OL].arXiv：1710.10903 [stat.ML].（2017-10-30）.https：//arxiv.org/abs/1710.10903.

[5] WU F，ZHANG T Y，SOUZA A H D S，et al. Simplifying Graph Convolutional Networks [J/OL].arXiv：1902.07153 [cs.LG].（2019-02-19）.https：//arxiv.org/abs/1902.07153v2.

[6] LI S，LI W Q，COOK C，et al. Independently Recurrent Neural Network （IndRNN）： Building a Longer and Deeper RNN [J/OL].arXiv：1803.04831 [cs.CV].（2018-03-13）.https：//arxiv.org/abs/1803.04831.

[7] BENESTY J，CHEN J，HUANG Y，et al. Pearson Correlation Coefficient [M]//COHEN I，HUANG Y，CHEN J，et al. Noise Reduction in Speech Processing.Berlin：Springer，2009：1-4.

[8] WANG Y，OMBAO H，CHUNG M K. Statistical Persistent Homology of Brain Signals [C]//ICASSP 2019-2019 IEEE International Conference on Acoustics， Speech and Signal Processing （ICASSP）.Brighton：IEEE，2019：1125-1129.

[9] 曹敏娜，陳俊杰，郭浩.基于多尺度腦網絡局部特征的抑郁癥分類 [J].計算機工程與設計，2018，39（12）：3712-3716.

[10] 胡章芳，張力，黃麗嘉，等.基于時頻域的卷積神經網絡運動想象腦電信號識別方法 [J].計算機應用，2019，39（8）：2480-2483.

[11] CHAZAL F. High-dimensional Topological Data Analysis [M]//GOODMAN J E，O'ROURKE J，TOTH C D. Handbook of Discrete and Computational Geometry： Third Edition.Boca Raton：Chapman and Hall/CRC，2017.

[12] GAUR P，GUPTA H，CHOWDHURY A，et al. A Sliding Window Common Spatial Pattern for Enhancing Motor Imagery Classification in EEG-BCI [J].IEEE Transactions on Instrumentation and Measurement，2021，70：1-9.

[13] ALCHIHABI A，EKMEKCI O，KIVILCIM B B，et al. Analyzing Complex Problem Solving by Dynamic Brain Networks [J].Frontiers In Neuroinformatics，2021，15：1-23.

[14] 鄭長坤，王海賢，顧凌云，等.基于腦電和肌電信號的下肢運動意圖識別方法 [J].中國醫療設備，2021，36（5）：61-66.

[15] 羅志增，魯先舉，周瑩.基于腦功能網絡和樣本熵的腦電信號特征提取 [J].電子與信息學報，2021，43（2）：412-418.

[16] NAKAJIMA J，WEST M. Dynamics & Sparsity in Latent Threshold Factor Models： A Study in Multivariate EEG Signal Processing [J].Brazilian Journal of Probability and Statistics，2017，31（4）：701-731.

作者簡介：盛志林（1999—），男，漢族，江西新余人，碩士在讀，研究方向：智能數據分析與應用。