不同形狀石英砂三軸剪切失穩研究

劉鑫 徐新鈺 黃良 鐘源

摘?要：為探究砂土形狀對剪切失穩特性的影響，首先通過顯微圖像采集與處理技術，對相同粒徑和級配、不同形狀的石英砂進行了顆粒形狀分析；然后在應力控制條件下進行了不排水三軸剪切試驗，建立了基于應變速率增量（ΔSR）的石英砂失穩判據；最后通過PFC2D模擬了不同形狀顆粒柱的坍塌試驗并對失穩機理進行了探討。結果表明：ΔSR可作為一種新手段判別砂土是否發生失穩；形狀規則砂樣會出現“假失穩點”，且峰值點也是失穩點，而形狀不規則砂樣的峰值點滯后于失穩點；在應力控制條件下，形狀規則砂樣的應力路徑呈“鋸齒狀”發展、超靜孔隙水壓力和軸向應變呈“階梯式”發展，而形狀不規則砂樣的試驗曲線未出現突變；不同形狀砂樣在失穩時表現出的差異與顆粒間的能量轉換機制以及接觸運動形式有關。研究成果可為邊坡的穩定分析以及滑坡等地質災害的預防提供參考。

關鍵詞：砂；顆粒形狀；失穩；應力控制；三軸試驗

中圖分類號：TU 411

文獻標志碼：A

文章編號：1672-9315（2024）03-0532-11

DOI：10.13800/j.cnki.xakjdxxb.2024.0313開放科學（資源服務）標識碼（OSID）：

Study on triaxial shear instability of quartz sand

with different shapes

LIU Xin1，XU Xinyu1，HUANG Liang1，2，ZHONG Yuan3

（1.School of Geological Engineering and Geomatics，Changan University，Xian 710054，China；

2.School of Engineering，China University of Geosciences，Wuhan 430074，China；

3.China West Airport Group Co.，Ltd.，Xian 710075，China）

Abstract：In order to investigate the influence of particle shape on the shear instability characteristics of sand，

the particle shape analysis of quartz sand with the same gain size and gradation，but with different shape was firstly made by using the microscopic image acquisition and processing techniques.Then the undrained triaxial shear tests were conducted under stress controlled condition，with a instability criterion

established

based on the strain rate increment（ΔSR）.Finally，the collapse tests of granular columns with different particle shape were simulated by PFC2D and the mechanism of destabilization was examined.The results show that ΔSR can be used as a new means to determine whether the sand is instable or not.When the value of ΔSR is continuously shaken，the sample has a large cumulative deformation，and the sample becomes instable.The instability point is also the peak point in the sand samples with regular particle shape.And the samples exhibit a “false instability point”，which shows that the shear stress of the samples decreases and increases suddenly with the development of strain during the shear process.On the other hand，the peak point of the irregularly-shaped sand samples lagged behind the instability point.Under stress controlled condition，the stress path of the regular-shaped sand samples is in a “jagged” pattern，and the excess pore pressure and axial strain are in “stepped” patterns，but the test curves of the irregular sand samples do not show any sudden changes.The difference of instability of sand samples with different shapes is related to the energy conversion mechanism and contact motion formed between particles.The research results could provide a reference for slope stability analysis and

a guidance for

prevention of geological disasters such as landslides.

Key words：sand；particle shape；instability；stress control；triaxial test

0?引?言

影響砂土力學特性的因素包括密度、有效圍壓、粒徑級配和顆粒形狀等[1

-2]。其中，由于砂土的形狀分析需要借助圖像處理手段，在工程實踐中最容易被忽略。而越來越多的研究發現，不同形狀的砂土通過顆粒的排列方式及接觸形式改變其力學行為[3-8]，因此，亟需在砂土的強度和變形分析中考慮形狀差異所帶來的影響。 國內外學者圍繞砂土形狀如何定量描述和如何影響其力學特性進行了大量研究。1932年，WADELL首先提出了球度（S）和圓度（R）概念，分別用來描述顆粒與規則圓球的差異程度和棱角的銳利程度[9]；此后，上述形狀參數被廣泛應用于建立砂土形狀和強度參數的研究中[10-13]。其中，CHO等在分析形狀參數時，將S和R的平均值定義為規則度（ρ），發現砂土的不規則程度增大，試樣的最大、最小孔隙比（emax/emin）也增大，而其剪切剛度減小[10]。近年來，YANG等采用福建砂、玻璃珠和碎玻璃珠的混合樣進行了三軸剪切試驗，發現不規則形狀的顆粒通常有較高的抗液化強度，并且顆粒的形狀差異還會影響臨界狀態特性，表現為顆粒的形狀越不規則，其臨界狀態摩擦角越大[14-15]；此外，LIU和YANG還基于彎曲元試驗結果建立了波速和砂土形狀參數的函數關系[16]；黃良等以鈣質砂為研究對象，提出用偏離度（α）定量描述顆粒偏離圓球的不同趨勢，并通過三軸剪切試驗發現試樣的不排水剪切強度與偏離度有較好的相關性[17]。值得注意的是，研究砂土形狀和力學特性時一般在應變控制下施加靜荷載，試樣的軸變速率在加載中維持不變，換句話說，應變控制試驗不能真實地反映試樣的失穩特性[18-21]。因此，研究這一問題必然要采用應力控制試驗，這對于邊坡穩定分析、滑坡等地質災害的預防[22-24]具有參考意義，而目前對于砂土形狀如何影響其剪切失穩特性仍然不清楚。為此，首先選取不同形狀的石英砂開展了顆粒形狀量化分析；然后通過應力控制下不排水三軸試驗研究了形狀對其失穩特性的影響；最后通過離散元顆粒柱坍塌模擬試驗進一步對砂土形狀的影響進行了探討。

1?試驗材料及方法

1.1?試驗材料試驗采用2種礦物成分和級配相近、形狀差異明顯的石英砂，分別是顆粒形狀相對圓潤的渥太華砂（OS）和多棱角的白石英砂（WS）。同時，為了排除粒徑和級配等干擾因素，試驗前通過篩分配置相同級配的砂土。試驗材料的級配曲線和顯微鏡下的照片如圖1所示，基本物理參數見表1。

1.2?形狀參數測定試驗方法

1.2.1?顆粒圖像獲取和處理首先將篩分后的試樣洗凈、低溫烘干，以消除雜質對結果造成的誤差；然后分別選取渥太華砂和白石英砂顆粒各1 000個，使用顯微鏡（LEICA-MC190HD）采集圖像；最后采用Image-Pro Plus 6.0（IPP6.0）圖像處理軟件對獲取的圖像進行處理。選取縱橫比（AR）、球度（S）和圓度（R）3種形狀參數對顆粒形狀進行量化分析，不同形狀參數的示意圖與對應的計算公式[16]如圖2所示，顆粒形狀基本參數定義見表2。

1.2.2?顆粒形狀量化分析在統計學中，箱形圖常被用來描述數據的分布情況，其最大的優點是不受異常值的影響[25]。LI等[25]及WANG等[26]都采用了箱型圖來統計石灰巖等爆破碎片的平坦指數和鈣質砂的顆粒形狀參數，并對箱型圖進行了詳細介紹，其結構示意圖如圖3所示。

1.3?應力控制剪切及波速測試試驗方法

1.3.1?試驗裝置采用英國VJ Tech公司生產的全自動三軸儀，軸向加載由伺服電機控制，應力加載速率在 0.1～50 N/min之間任意可調，儀器還改造安裝了彎曲元波速測試系統，用來輔助分析土體的剪切失穩特性。彎曲元由兩片長度可伸縮的壓電陶瓷片和中間的金屬墊片粘合而成，并依次采用絕緣、防水材料進行外包，根據壓電陶瓷片接線方式的不同（如串聯或并聯），可分別實現剪切波信號的發射和接收[27]。完整的測試系統如圖4所示，包括彎曲元的一對發射器和接收器、信號處理器、電源、示波器以及控制激發信號的一套軟件系統。其中，彎曲元尺寸的寬度為11 mm，厚度為1.2 mm，完全插入土體時深度為2 mm，發射器和接收器分別內嵌于頂帽和底座的中心處。試驗中，輸入信號采用單脈沖正弦波，激振頻率為5 kHz，振幅大小為±7 V。

1.3.2?試樣制備與試驗方案采用濕法制備直徑D=50 mm，高度H=100 mm的圓柱體試樣，具體步驟為：①取適當質量砂土加入5%的無氣水混合均勻；②根據試樣的預設相對密實度，在制樣器內分5層逐層壓實；③安裝頂帽同時對試樣施加25 kPa的吸力使其固定，拆除制樣器并測量試樣的尺寸。該制樣方法的優點在于能夠制備非常松散的試樣，同時能有效保證試樣的均勻性[28]。另外，測試前需對試樣進行飽和，參照文獻對試樣依次通二氧化碳和無氣水淋濾處理，再設置分級反壓飽和至圍壓330 kPa、反壓300 kPa，直到孔壓系數滿足B≥0.95[29-32]，此時認為試樣完全飽和，然后對試樣進行固結。當試樣的排水穩定，則認為試樣固結完成，隨后進行應力控制三軸不排水剪切試驗，加載速率為0.5 N/min。在試樣的剪切過程中，采用LVDT記錄試樣的軸向變形，同時進行剪切波速測試。具體的試驗方案見表3。

1.3.3?變量定義說明依照《土工試驗方法標準》（GB/T50123—2019），試驗中的變量定義為

ε1=（hc-h）/hc

（1）

q=ΔF/As

（2）

As=Ac/（1-0.01ε1）

（3）

p′=（q+3×σ３′）/3

（4）

式中?ε1為軸向應變，%；hc為試樣的固結后高度，cm；h為試樣剪切過程中的高度，cm；q為剪應力，kPa；ΔF為試樣剪切過程中軸力的變化，kPa；As為剪切過程中的橫截面積，可通過試樣固結后的面積Ac和軸向應變ε1換算得到，cm2；p′為平均有效應力，kPa；σ3′為有效圍壓，kPa。

2?結果分析與討論

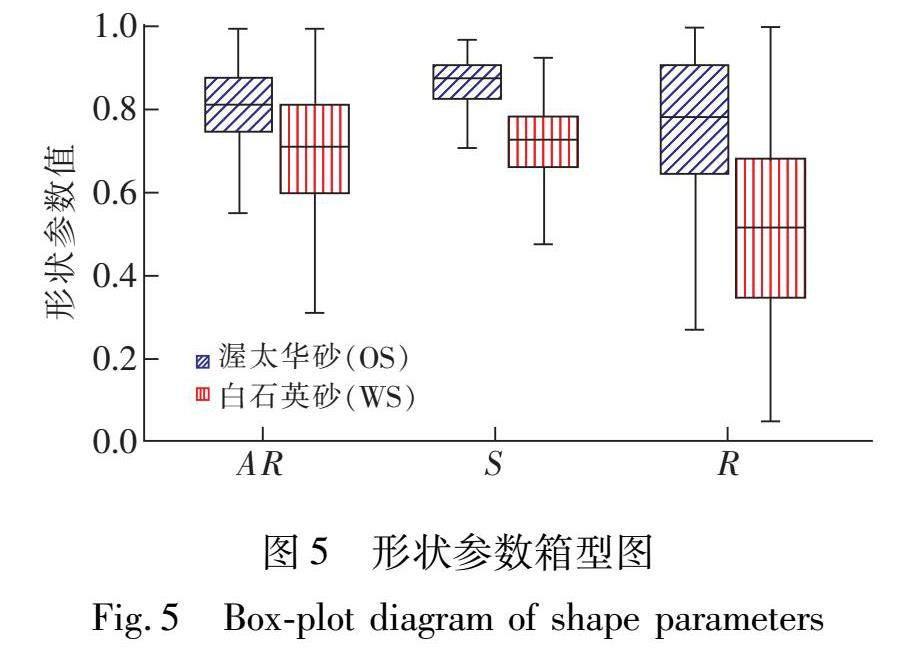
2.1?顆粒形狀量化分析結果圖5分別對比了2種砂土的形狀參數，包括縱橫比（AR）、球度（S）和圓度（R）。對于同一種砂，R的分布區間明顯大于

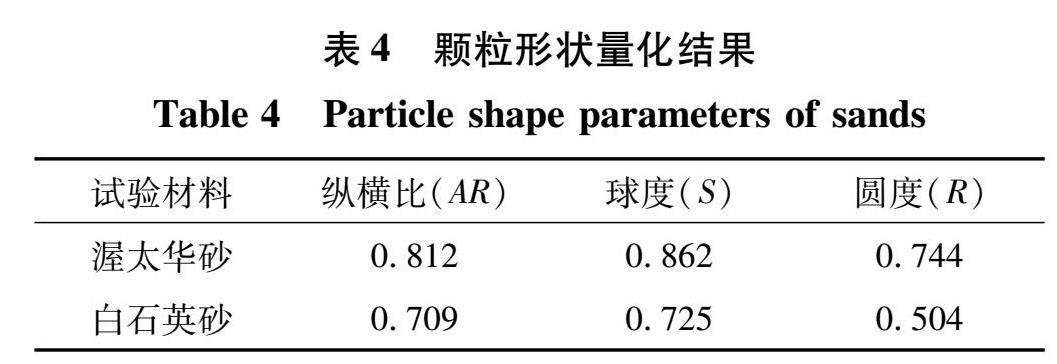
AR和S的分布區間，即R的差異更大，這說明2類砂土的不規則性主要受圓度控制；另一方面，白石英砂（WS）的箱體長度比渥太華砂（OS）大，說明白石英砂的形狀差異較大、形狀更不規則。圖5中各樣本的中位數見表4。

從圖1觀察顆粒的形狀與表4中形狀參數可知，與白石英砂相比，渥太華砂的各形狀參數接近于1，表現為形狀上更加圓潤。

2.2?砂土失穩點的判斷研究土體失穩通常以應變發展出現拐點為依據，而僅從應變和時間圖上來看這一拐點并不清楚（圖6（b）），這導致了在判斷試樣失穩時會出現偏差。此外，土體的失穩還可以基于二階功準則判斷，即土體的失穩條件為

d2w=dσ′∶dε≤0；‖dε‖≠0

（5）

式中?d2w為二階功；dσ′為有效應力增量；dε為相應的應變增量。由上式可知，在應變控制不排水三軸剪切試驗中，dε始終為正，因此有效應力增量會出現負值即失穩點，換句話說，剪應力的峰值點即失穩點。而工程實踐中較難獲取土體的有效應力增量dσ′，因此通過二階功進行失穩判斷的局限性很大。此外，土體受飽和度、密實度及應力狀態等多種因素影響，失穩點可能并非峰值強度點[18，20，33-35]。例如，CHU和 LEONG用飽和松砂進行三軸應力控制試驗，發現不同固結應力路徑下的試樣的失穩點在峰值點之后[18]。針對以上問題，首次提出了用應變速率增量（ΔSR）來判斷試樣是否發生失穩，可表述為

SRn=

ε1n-ε1（n-1）

tn-tn-1

（6）

ΔSR=SRn-SRn-1

（7）

式中?SRn為應變速率，%/min；ε1n為當前tn時刻的軸向應變，%；ε1（n-1）為前一時刻（t（n-1））的軸向應變，%。當ΔSR數值發生持續的劇烈抖動時，表明試樣有較大的累積變形，此時試樣發生失穩，其剛度模量明顯減小，導致無法維持穩定的軸力[36]。將2種不同形狀砂樣（OS-2、WS-2）的應變速率增量（ΔSR）、軸向應變和剪切波速隨時間變化的曲線繪制于圖6中。值得注意的是，剪切波速可以反映土體的剛度變化，被認為是滑坡先兆的判據之一[36-37]。形狀規則的砂樣（

OS-2）雖然在t=120 min和t=136 min（點b-1、b-2）時出現了劇烈抖動，但之后逐漸穩定，且點b-1、b-2應變無較大增長、波速變化較小，因此將點b-1、b-2稱為“假失穩點”。當t=168 min時（紅色圓點），ΔSR出現劇烈抖動，之后應變快速增長、剪切波速減小，認為此處是試樣真正的失穩點。另一方面，形狀不規則砂樣（WS-2）并未出現“假失穩”情況，而是直接發生失穩。

圖7為100 kPa有效圍壓下試樣的軸力變化曲線。采用上述方法對各組試樣的峰值點、失穩點分析選取并標記。從圖7可以看到，形狀規則砂樣（OS）出現了黏滑行為，而形狀不規則砂樣（WS）的軸向力在爬升階段基本平穩。崔德山等采用圓形的玻璃珠進行三軸試驗，發現試樣的剪應力會隨應變發展出現突然減小又突然增大的行為，認為該現象與顆粒間的摩擦形式有關[38]，這與觀察到的渥太華砂（OS）的黏滑現象類似，耿乃光和劉曉紅也有類似發現[39]。此外，試樣的軸力在達到失穩點后迅速降低，之后又出現爬升，但由于此時試樣破壞速度較快且已經發生較大的變形（最大到20%），不能代表土體實際的剪切特性（非穩定行為）[18]，因此在圖7～11中用虛線表示。圖8為100 kPa有效圍壓下各組試樣的應力路徑，不同形狀砂樣均呈軟化趨勢；對形狀規則砂樣（OS）而言，失穩點即峰值點，且應力路徑呈現“鋸齒狀”發展。而形狀不規則砂樣（WS）的峰值點略滯后于失穩點，且應力路徑相對平滑。

圖9所示為100 kPa有效圍壓下各組試樣的超靜孔隙水壓力變化曲線。從圖9可以看出，形狀規則砂樣（OS）的超靜孔隙水壓力隨時間先緩慢增長，之后出現“階梯式”突變，即超靜孔隙水壓力突然上升又繼續保持穩定，在第2次突變時發生失穩破壞，表現為孔壓幾乎垂直增加；而不規則砂樣（WS）的超靜孔隙水壓力隨時間平滑增長，以WS-1為例，在失穩點之前其孔壓增長速率較小，約為0.18 kPa/min，失穩點之后逐漸增大至1.06 kPa/min。而當超靜孔隙水壓力達到強度峰值點之后，其孔壓增長速率迅速增大（最大速率約為6.21 kPa/min）。圖10為100 kPa有效圍壓下各組試樣的軸向應變發展曲線。2種試樣均在較小應變（

ε1<1%）時承受了較大應力，之后試樣發生破壞，應變迅速發展；此外，應變發展與其超靜孔隙水壓力發展類似，形狀規則砂樣（OS）隨時間呈現“階梯狀”，而不規則砂樣（WS）隨時間平滑增長。這可能與渥太華砂（OS）較為圓潤、棱角少有關，即顆粒與顆粒之間的咬合力較小，因此造成軸變階梯式跳躍，從而造成孔壓的增長。上述猜想可從2.3節的數值模擬結果進行驗證。

此外，還研究了較大圍壓（σ3′=300 kPa）下試樣的剪切失穩行為。試驗曲線如圖11所示，從圖中可以看到高圍壓下不同形狀試樣表現出與低圍壓相類似的性質，即應力路徑呈“鋸齒狀”發展、超靜孔隙水壓力呈“階梯式”發展。這說明顆粒形狀導致的試樣差異失穩現象與圍壓大小無關。

2.3?基于顆粒柱坍塌的微觀機理探討與分析上述應力控制三軸剪切試驗的目的是為了研究斜坡的失穩過程，并最終解決斜坡在自重荷載作用下的穩定性問題，而顆粒柱坍塌試驗同樣為應力控制，且能更好地展示這一過程。因此，文中嘗試采用離散元軟件PFC2D建立坍塌柱數值模型來探究不同形狀影響下顆粒材料的失穩特性。模型通過抽離擋板實現顆粒柱的坍塌，模型中采用圓形和3個圓形顆粒連接形成的類三角形顆粒簇研究不同形狀顆粒的影響，其中圓形顆粒對應相對圓潤的渥太華砂，類三角形顆粒對應棱角多的白石英砂。模型示意如圖12所示，模型參數見表5。

圖13給出了2種不同形狀顆粒組成的顆粒柱，從崩塌開始到運動結束整個系統的歸一化重力勢能Ep/E0、歸一化動能Ek/E0、歸一化耗散能Ediss/E0 [40]隨坍塌時間的演變。從圖14可以看到，擋板抽離時（t=0），勢能逐漸轉化為動能和耗散能，動能1 s內達到峰值后快速下降，而耗散能持續增長；形狀不規則的顆粒試樣（類三角形顆粒）勢能減小的更少，因此達到穩定狀態耗散的能量也更少，這說明顆粒間的咬合力一定程度上使試樣整體更穩定。

顆粒形狀會影響其動能的本質可能是接觸方式的不同，因此引入滑動因子[13]這一概念，其定義如下

Sc=|fct|/（μfcn）

（8）

式中?fct和fcn分別為接觸c的切向接觸力和法向接觸力；μ為接觸摩擦系數，認為Sc>0.999 9時接觸發生滑動[13，41]。

在此基礎上定義接觸滑動率為發生滑動的接觸數除以總接觸數。圖14（a）為不同形狀組成

顆粒柱滑動接觸率隨時間的變化趨勢，可以看到不

同

形狀試樣變化趨勢基本一致，快速增加到峰值然后穩定；此外隨顆粒形狀的不規則性增加（圓形→類三角形），滑動接觸率有所增長。從圖14（b）中可以看出，相同初始狀態下，圓形顆粒柱發生轉動的顆粒數較多，旋轉角度較大，而類三角形顆粒轉動角度較小，發生轉動的顆粒較少。這說明，在坍塌試驗初期，類三角形顆粒由于存在棱角，其抗轉動能力強于圓形顆粒，迫使顆粒接觸發生滑動而非轉動以調整試樣的整體變形。整體來看，圓形顆粒旋轉角度大，能量耗散多；類三角形顆粒轉動角度小，能量耗散少。因此，能量變化也和顆粒轉動角度有關。

另外，圖15為2種不同形狀顆粒組成的顆粒柱在坍塌過程中的顆粒位移變化，從圖中可以看出圓形顆粒有更小的堆積高度和更大的跑出距離。當坍塌結束后，圓形顆粒表面輪廓與水平面形成的角度α約為20.8°，小于類三角形顆粒的33.1°。

由于坍塌柱試驗為應力控制，因此，其失穩機理與三軸應力控制剪切的失穩機理有相似之處。綜合分析圖13～15，推測在應力控制三軸試驗中，不同形狀砂土顆粒表現出的失穩差異可能與顆粒間的能量轉換機制和運動形式有關。規則顆粒

間的咬合力較小，在自重作用下更容易轉動，導致形狀規則砂樣應力路徑的“鋸齒狀”發展；而不規則顆粒間的互鎖作用強，抗轉動能力更強，從而形狀不規則砂樣的試驗曲線基本平穩發展，未出現突變。

3?結?論

1）首次提出了應變速率增量（ΔSR），用來判斷試樣是否發生失穩。剪切波速與軸向應變的發展表明ΔSR可較好地判斷試樣是否失穩，能作為一種新手段判斷土體是否發生失穩。2）形狀規則砂樣（渥太華砂）容易出現“假失穩點”，失穩點即峰值點，而形狀不規則砂樣（白石英砂）峰值點滯后于失穩點。

3）形狀規則砂樣應力路徑呈“鋸齒狀”發展，超靜孔隙水壓力和應變呈“階梯式”發展。而形狀不規則砂樣試驗曲線基本平穩發展，呈現平滑趨勢，未出現突變。

4）不同形狀砂樣表現出的失穩差異性可能與顆粒間的能量轉換機制和接觸運動形式有關。參考文獻（References）：

[1]?王貴榮，董晨，段釗，等．粗顆粒組分含量對中細砂抗剪強度的影響[J]．西安科技大學學報，2020，40（1）：24

-30．WANG Guirong，DONG Chen，DUAN Zhao，et al．Effect of coarse particle content on shear strength of medium sand[J]．Journal of Xian University of Science and Technology，2020，40（1）：24-30．

[2]姚超偉，王凱，王璐，等．平均粒徑和粗糙度對砂-玻纖網格布界面剪切特性[J]．西安科技大學學報，2023，43（5）：923-932．YAO Chaowei，WANG Kai，WANG Lu，et al．Shear properties of the interface between sand-fiber glass grid cloth with mean particle size and roughness[J]．Journal of Xian University of Science and Technology，2023，43（5）：923-932．

[3]劉清秉，項偉，LEHANE B M，等．顆粒形狀對砂土抗剪強度及樁端阻力影響機制試驗研究[J]．巖石力學與工程學報，2011，30（2）：400-410．LIU Qingbing，XIANG Wei，LEHANE B M，et al．Expe-rimental study of effect of particle shapes on shear strength of sand and tip resistance of driven piles[J]．Chinese Journal of Rock Mechanics and Engineering，2011，30（2）：400-410．

[4]劉清秉，項偉，BUDHU M，等．砂土顆粒形狀量化及其對力學指標的影響分析[J]．巖土力學，2011，32（S1）：190-197．LIU Qingbing，XIANG Wei，BUDHU M，et al．Study of particle shape quantification and effect on mechanical property of sand[J]．Rock and Soil Mechanics，2011，32（S1）：190-197．

[5]MISKIN M Z，JAEGER H M．Adapting granular materials through artificial evolution[J]．Nature Materials，2013，12（4）：326331．

[6]GAN J Q，YU A B．DEM simulation of the packing of cylindrical particles[J]．Granular Matter，2020，22（1）：1-19．

[7]吳楊，崔杰，李能，等．島礁吹填珊瑚砂力學行為與顆粒破碎特性試驗研究[J] ．巖土力學，2020，41（10）：3181-3191． WU Yang，CUI Jie，LI Neng，et al．Experimental study on the mechanical behavior and particle breakage cha-racteristics of hydraulic filled coral sand on a coral reef island in the South China Sea[J]．Rock and Soil Mechanics，2020，41（10）：3181-3191．

[8]李能，吳楊，周福霖，等．島礁吹填珊瑚砂不排水單調和循環剪切特性試驗[J] ．中國公路學報，2023，36（8）：152-161．LI Neng，WU Yang，ZHOU Fulin，et al．Experiment of undrained monotonic and cyclic shear characteristics of hydraulic filled coral sand from reef island[J]．China Journal of Highway and Transport，2023，36（8）：152-161．

[9]WADELL H．Volume，shape，and roundness of rock particles[J]．The Journal of Geology，1932，40（5）：443-451．

[10]CHO G C，DODDS J，SANTAMARINA J C．Particle shape effects on packing density，stiffness，and strength：Natural and crushed sands[J]．Journal of Geotechnical and Geoenvironmental Engineering，2006，132（5）：591-602．

[11]GUO P J，SU X B．Shear strength，interparticle locking，and dilatancy of granular materials[J]．Canadian Geotechnical Journal，2007，44（5）：579-591．

[12]楊貴，許建寶，孫欣，等．顆粒形狀對人工模擬堆石料強度和變形特性影響的試驗研究[J]．巖土力學，2017，38（11）：3113-3118，3153．YANG Gui，XU Jianbao，SUN Xin，et al．Experimental study of influence of particle shape on strength and deformation for artificial rockfill materials[J]．Rock and Soil Mechanics，2017，38（11）：3113-3118，3153．

[13]NIE Z H，ZHU Y G，WANG X，et al．Investigating the effects of Fourier-based particle shape on the shear behaviors of rockfill material via DEM[J]．Granular Ma-tter，2019，21（2）：1-15．

[14]YANG J，LUO X D．Exploring the relationship between critical state and particle shape for granular materials[J]．Journal of the Mechanics and Physics of Solids，2015，84：196-213．

[15]YANG J，LUO X D．The critical state friction angle of granular materials：Does it depend on grading？[J]．Acta Geotechnica，2018，13（3）：535-547．

[16]LIU X，YANG J．Shear wave velocity in sand：Effect of grain shape[J]．Géotechnique，2018，68（8）：742-748．

[17]黃良，劉鑫，蘭恒星．鈣質砂特征形狀分析及不排水剪切強度研究[J]．工程地質學報，2024，32（2）：378-386．HUANG Liang，LIU Xin，LAN Hengxing．Investigation on characteristic shape of calcareous sand and associated effect on undrained shear strength[J]．Journal of Engineering Geology，2024，32（2）：378-386．

[18]CHU J，LEONG W K．Pre-failure strain softening and pre-failure instability of sand：A comparative study[J]．Géotechnique，2001，51（4）：311-321．

[19]周秋娟，陳曉平，黃麗娟．應力控制式三軸儀的改裝及應用[J]．地下空間與工程學報，2011，7（3）：469-473，557．ZHOU Qiujuan，CHEN Xiaoping，HUANG Lijuan．Reconstruction and application of the stress control tri-axial apparatus[J]．Chinese Journal of Underground Space and Engineering，2011，7（3）：469-473，557．

[20]WANATOWSKI D，CHU J．Factors affecting pre-failure instability of sand under plane-strain conditions[J]．Géotechnique，2012，62（2）：121-135．

[21]馮大闊，張建民．應力幅值比對土-結構接觸面非共軸特性影響研究[J]．巖土力學，2022，43（11）：1-12．FENG Dakuo，ZHANG Jianmin．Role of stress amplitude ratio in the non-coaxial behavior of the interface between gravel and structure[J]．Rock and Soil Mechanics，2022，43（11）：1-12．

[22]陳練武．陜西省耀州區滑坡崩塌發育規律研究[J]．西安科技大學學報，2005，25（2）：164-167.CHEN Lianwu．Landslides and dilapidations in Yaozhou district[J]．Journal of Xian University of Science and Technology，2005，25（2）：164-167．

[23]劉冬，彭建兵，葉萬軍，等．秦嶺山區宜居鄉村的架構思考[J]．西安科技大學學報，2023，43（4）：743-751．LIU Dong，PENG Jianbing，YE Wanjun，et al．The systematic architecture of livable countryside in Qinling Mountains[J]．Journal of Xian University of Science and Technology，2023，43（4）：743-751．

[24]蘭恒星，彭建兵，祝艷波，等．黃河流域地質地表過程與重大災害效應研究與展望[J]．中國科學：地球科學，2022，52（2）：199-221．LAN Hengxing，PENG Jianbing，ZHU Yanbo，et al．Research on geological and surfacial processes and major disaster effects in the Yellow River Basin[J]．Science China Earth Sciences，2022，52（2）：199-221．

[25]LI R Z，LU W B，CHEN M，et al．Quantitative analysis of shapes and specific surface area of blasted fragments using image analysis and three-dimensional laser scanning[J]．International Journal of Rock Mechanics and Mining Sciences，2021，141：104710．

[26]WANG T Y，MA L J，WANG M Y，et al．Effects of particle shape on dynamic mechanical behaviours of coral sand under one-dimensional compression[J]．Engineering Geology，2022，304：106624．

[27]LIU X，WEI X，QIN H．Characterizing compressive strength of compacted saline loess subjected to freeze-thaw cycling with wave velocity[J]．Bulletin of Engineering Geology and the Environment，2022，81（4）：168．

[28]LADD R S．Preparing test specimens using under compaction[J]．Geotechnical Testing Journal，1978，1（1）：16-23．

[29]YANG J，LIU X．Shear wave velocity and stiffness of sand：The role of non-plastic fines[J]．Géotechnique，2016，66（6）：1-15．

[30]LIU X，WANG Y C，NAM B H．Characterizing un-drained shear behavior of loess subjected to K0 loading condition[J]．Engineering Geology，2022，302：106634．

[31]劉鑫，苗雪青，黃良，等．5種排水條件下飽和重塑黃土三軸剪切特性[J]．吉林大學學報（地球科學版），2023，53（5）：1499-1509．LIU Xin，MIAO Xueqing，HUANG Liang，et al．Triaxial shear behavior of saturated remolded loess subjected to five drainage conditions[J]．Journal of Jilin University（Earth Science Edition），2023，53（5）：1499-1509．

[32]LIU X，HUANG G J，QIN Z H，et al．Shear behaviour of loess under varied drainage conditions subjected to mo-notonic and cyclic loads[J]．Soil Dynamics and Earthquake Engineering，2024，177：108397．

[33]LADE P V．Static instability and liquefaction of loose fine sandy slopes[J]．Journal of Geotechnical and Geoenviromental Engineering，1992，118（1）：51-71．

[34]呂璽琳，賴海波，黃茂松．飽和土體靜態液化失穩理論預測[J]．巖土力學，2014，35（5）：1329-1333，1339．LYU Xilin，LAI Haibo，HUANG Maosong．Theoretically predicting instability of static liquefaction of saturated soils[J]．Rock and Soil Mechanics，2014，35（5）：1329-1333，1339．

[35]呂璽琳，錢建固，黃茂松．不排水加載條件下K0固結飽和砂土失穩預測[J]．巖土工程學報，2015，37（6）：1010-1015．LYU Xilin，QIAN Jiangu，HUANG Maosong．Prediction of instability of K0-consolidated saturated sands under undrained loading conditions[J]．Chinese Journal of Geotechnical Engineering，2015，37（6）：1010-1015．

[36]陳宇龍，內村太郎．降雨誘發土坡失穩過程中彈性波波速演化規律的模型試驗研究[J]．巖石力學與工程學報，2019，38（10）：2138-2150．CHEN Yulong，UCHIMURA Taro．Model tests of evaluation behaviors of the elastic wave velocity during the failure process of soil slopes due to rainfall[J]．Chinese Journal of Rock Mechanics and Engineering，2019，38（10）：2138-2150．

[37]秦輝，劉鑫，蘭恒星．用波速評價凍融循環作用下壓實黃土強度特性的試驗研究[J]．工程地質學報，2023，31（5）：1507-1515．QIN Hui，LIU Xin，LAN Hengxing．Evaluation of strength characteristics of compacted loess subjected to freeze-thaw cycling by wave velocity[J]．Journal of Engineering Geology，2023，31（5）：1507-1515．

[38]崔德山，項偉，陳瓊，等．顆粒材料黏滑運動特征與顆粒黏結試驗研究[J]．巖石力學與工程學報，2016，35（9）：1924-1935．CUI Deshan，XIANG Wei，CHEN Qiong，et al．Experimental study on stick-slip behaviour and sintering phenomenon of glass beads[J]．Chinese Journal of Rock Mechanics and Engineering，2016，35（9）：1924-1935．

[39]耿乃光，劉曉紅．四種巖石的摩擦滑動特征[J]．巖土工程學報，1987，9（3）：27-32．GENG Naiguang，LIU Xiaohong．The frictional characteristics of four kinds of rocks[J]．Chinese Journal of Geotechnical Engineering，1987，9（3）：27-32．

[40]崔溦，魏杰，王超，等．考慮顆粒級配和形態的顆粒柱坍塌特性離散元模擬[J]．巖土工程學報，2021，43（12）：2230-2239.CUI Wei，WEI Jie，WANG Chao，et al．Discrete element simulation of collapse characteristics of particle column considering gradation and shape[J]．Chinese Journal of Geotechnical Engineering，2021，43（12）：2230-2239．

[41]GONG J，LIU J．Effect of aspect ratio on triaxial compression of multi-sphere ellipsoid assemblies simulated using a discrete element method[J]．Particuology，2017，32：49-62．

（責任編輯：高佳）