基于數形結合的晶胞復習
賈同全
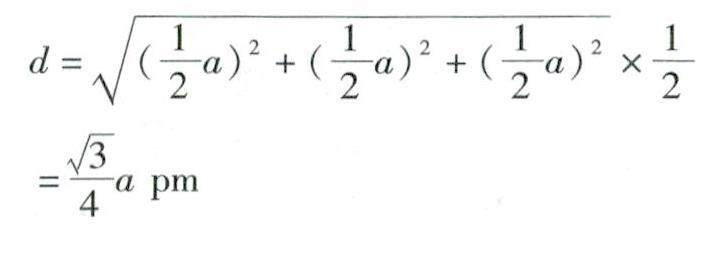
晶胞是描述晶體結構的基本單元,這個基本結構單元通常是一個平行六面體。晶體中晶胞的排列是無隙并置的,“無隙”指的是相鄰的晶胞之間共用頂角、共用棱、共用面。“并置”指的是從一個晶胞到另一個晶胞只需平移晶胞框架,無需任何轉動。
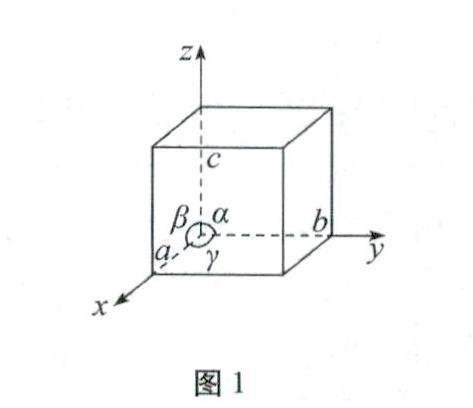
晶胞參數:3組棱長a、b、c;3組棱相互間的夾角α、β、γ(如圖1所示),中學化學常見晶胞如圖2所示。
立方晶胞:a=b=c,α=β=γ=90°(只有1個晶胞參數a是可變動的)。
四方晶胞:a=b≠c,α=β=γ=90°(有2個晶胞參數a和c)。
正交晶胞:a≠b≠c,α=β=γ=90°(有3個晶胞參數a、b和c)。
六方晶胞:a=b≠c,α=β90°,γ=120°(有2個晶胞參數a和c)。
一、準確描述晶胞質點空間位置的方法——原子分數坐標
1.定義:以晶胞參數為單位長度建立的坐標系來表示晶胞內部各原子的相對位置,稱為原子分數坐標。
2.原子分數坐標的確定方法:
①依據給出的坐標系取向和已知原子的坐標確定坐標原點。
②一般以坐標軸所在立體圖形的棱長為1個單位(長、寬、高可以不同,但都為1個單位)。
③從原子所在位置分別向x、y、z軸作垂線,所得坐標軸上的截距即為該原子的分數坐標(各點均在晶胞內,0≤x、y、z<1)。
二、晶胞中粒子的投影
1.定義:用一組光線將物體的形狀投射到一個平面上去,稱為投影。在該平面上得到的圖像,也稱為投影圖。
2.分類:
①正投影:投射線的中心線垂直于投影的平面。②斜投影:投射線的中心線不垂直于投影的平面。
目前大多數題目涉及到的都是正投影。
3.常見晶胞結構模型圖的坐標軸方向(俯視圖)和體對角線方向投影圖總結。
(1)體心立方晶胞(如圖3所示)
俯視圖:8個頂點投影在正方形4個頂點上,體心投影在正方形中心。
體對角線方向投影圖:6個頂點投影在正六邊形頂點上,另外2個頂點和體心重疊在正六邊形中心。
(2)面心立方晶胞(如圖4所示)
俯視圖:8個頂點投影在正方形4個頂點上,前后左右4個面心投影在正方形4個邊的中點,上下2個面心投影在正方形中心。
體對角線方向投影圖:6個頂點投影在大正六邊形頂點上,6個面心投影在小正六邊形頂點上,另外2個頂點重疊在正六邊形中心。
(3)金剛石晶胞(如圖5所示)
俯視圖:8個頂點投影在正方形4個頂點上,前后左右4個面心投影在正方形4個邊的中點,上下2個面心投影在正方形中心,左上右上左下右下四個小體心投影在4個小正方形中心。
體對角線方向投影圖:6個頂點投影在大正六邊形頂點上,3個面心和3個小體心(另3個面心在3個小體心背后遮擋)投影在小正六邊形頂點上,另外2個頂點和2個小體心重疊在正六邊形中心。
例題1 LiCl·3H2O屬于正交晶系(長方體形)。晶胞參數為0.75、1.0、0.56nm。如圖6所示為沿z軸投影的晶胞中所有氯原子的分布圖和原子分數坐標。
據此推斷該晶胞中氯原子數目為____。
解析可以根據投影圖將其轉化為立體圖(如圖7所示)。根據晶胞沿z軸的投影圖可知,該晶胞中氯原子①、②、③、④、A、B的位置,yz面上有2個氯原子①②,與yz平行的面上有2個氯原子③④,體內有2個氯原子A、B,所以1個晶胞中氯原子的數目為4×1/2+2=4。
三、晶胞中粒子間距的求算方法
要想求算晶胞中粒子間距,就必須了解清楚晶胞的結構。以金剛石為例,金剛石品胞(如圖8所示)中碳原子在什么位置相切?已知晶胞參數為apm,碳原子半徑與a之間有什么關系?
晶胞中的體對角線上(球①②③④⑤或球⑥⑦③⑧⑨)是球球相切(其中3,4,7號球為虛擬補充上去的),則有:8r=根號下3a。
例題2 普魯士藍晶體屬立方晶系,晶胞棱長為apm。鐵-氰骨架組成小立方體,Fe粒子在頂點,CN-在棱上,兩端均與Fe相連,立方體中心空隙可容納K+,如圖9所示(CN-在圖中省略)。
若所有鐵粒子為等徑小球,則K+與Fe2+之間最近距離為____pm;
解析鉀離子位于小立方體的體心,二價鐵位于小立方體的頂點,則
四、立方晶胞密度的計算模型
1.計算公式:ρ=m/V=n·M/NA·a3
2.思維流程:
①先確定一個晶胞中微粒個數n(均攤法)。
②再確定一個晶胞中微粒的總質量。
③根據晶胞參數a求晶胞的體積。
④最后代人密度公式求晶胞的密度。
3.單位換算:1pm=10-10cm;1nm=10-7cm。
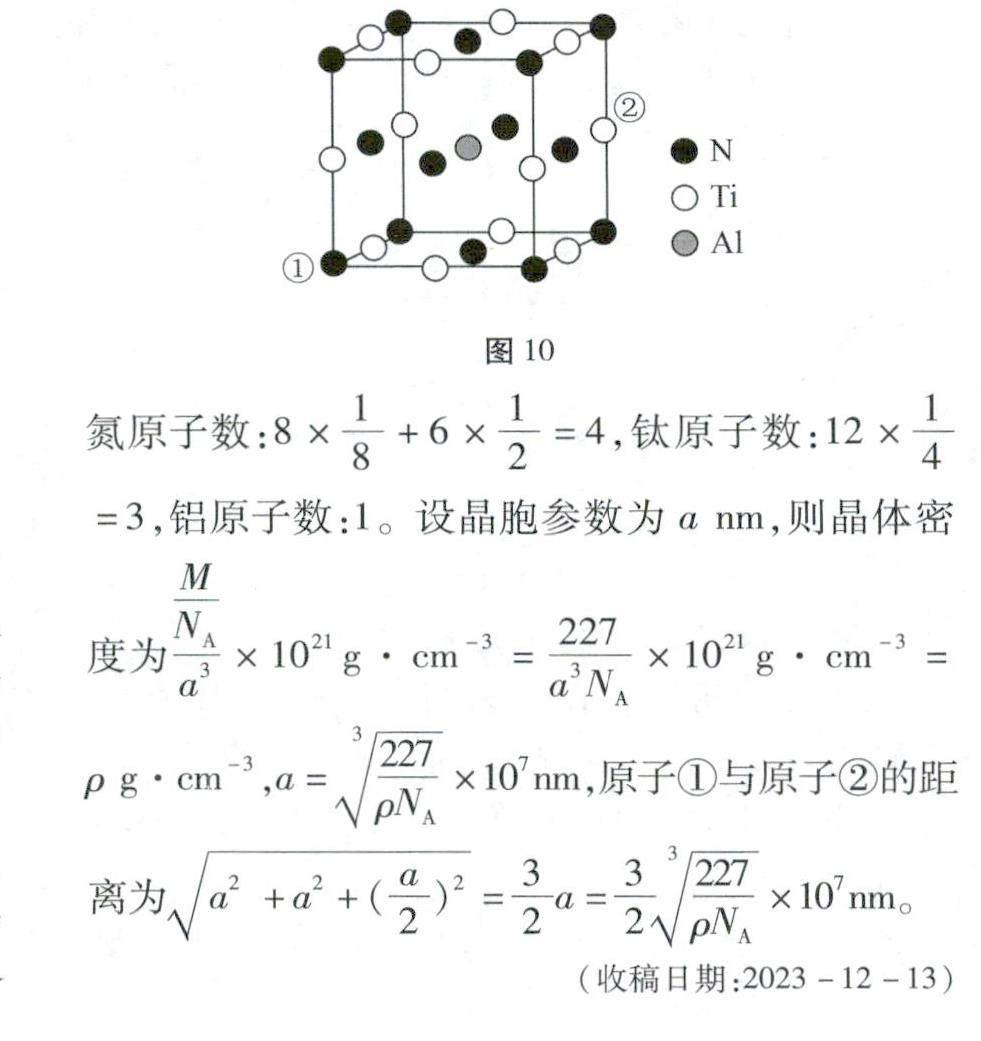
例題3 TiN晶胞中的少量Ti被Al代替后的立方晶胞結構如圖10所示。該晶胞中,距離Ti最近的Al有____個;原子①與原子②的距離為____nm(已知晶體密度為ρg·cm-3,阿伏加德羅常數的值為NA)。
解析 由圖可知,以右側棱心的鈦原子為例,晶胞內體心鋁原子與其最近,則周圍4個晶胞中距離Ti最近的Al有4個;據“均攤法”,晶胞中含氮原子數:

