微球殼在三維剪切流中的變形特性

張世昌 廖文博 陳鵬舉 沈冠東

DOI：10.20031/j.cnki.0254?6094.202403015

摘 要 利用雙向流固耦合的模擬方法，對三維剪切流中不同幾何參數的空心球殼和載液球殼的變形特性進行分析。研究發現，球殼在變形的同時伴隨著旋轉，且球殼上存在著交變應力，交變頻率取決于球殼旋轉速度。空心球殼相較于載液球殼變形更顯著，旋轉速度更快。

關鍵詞 微球殼 流固耦合 變形 旋轉 交變應力

中圖分類號 TQ050.3?? 文獻標志碼 A?? 文章編號 0254?6094（2024）03?0433?07

Deformation Characteristics of the Miniature Spherical Shell in

Three?dimensional Shear Flow

ZHANG Shi?chang1， LIAO Wen?bo1，CHEN Peng?ju1， SHEN Guan?dong1，2

（1. School of Mechanical and Power Engineering，Nanjing Tech University;

2. Graduate Students Division， Yancheng Teachers University）

Abstract? Making use of bidirectional fluid?structure coupling simulation to analyze? deformation characteristics of hollow spherical shells and liquid?loaded spherical shells with different geometric parameters in three?dimensional shear flow was implemented. The results show that， the rotation accompanies the deformation of the spherical shell and alternating stress exists on the spherical shell， and the alternating frequency depends on the rotation speed of the spherical shell. The hollow spherical shells deformation is more significant and the rotation speed is faster than that of the liquid?carrying spherical shell.

Key words?? miniature spherical shell， fluid?solid coupling， deformation， rotation， alternating stress

作者簡介：張世昌（1995-），碩士研究生，從事流固耦合的研究，mrzhangshichang@163.com。

引用本文：張世昌，廖文博，陳鵬舉，等.微球殼在三維剪切流中的變形特性[J].化工機械，2024，51（3）：433-439.

球殼結構具有良好的承載性能，能以較小的厚度承受較大的荷載，同時具有良好的穩定性。無論是大尺度球殼還是微尺度球殼，在工程中的應用都十分廣泛，常用作儲存容器、保護殼、建筑物或其他構件。例如，微膠囊作為一種微型球殼結構，在化工、儲能、傳熱及生物醫學等領域有著重要作用。無論是空心球殼亦或是載液球殼，受殼體自身幾何尺寸及所處流場環境的影響，可能會發生變形、旋轉，進而產生交變應力，引起殼體的疲勞失效。研究人員對球殼結構在流場中的研究主要集中于細胞、微膠囊[1，2]等微球形結構在流場中的變形特性。細胞和微膠囊都屬于微球殼結構，皆由球形外殼或膜與內部物質構成。因此，研究時通常將其視為彈性球殼[3，4]，以分析其在流場中的變化。總之，由于懸浮在流場中的固體球殼既無固定支撐，又存在運動和變形的耦合，理論和試驗研究的難度較大，因此對其相關研究較少。

對于空心球殼在剪切流場中的變形，BARTH?S?BIESEL D建立了單個球形空殼在簡單剪切流和平面雙曲流中的模型，使用初始預應力來評估球殼結構的機械性能[5];POZRIKIDIS C建立了球殼變形的數值計算方法，研究了剪切流中彎曲剛度對變形的影響[6];DE LOUBENS C等在線彈性條件下通過兩個交叉實驗分別獲取了剪切流場中彈性空殼的剪切模量及體積模量，揭示了球殼變形時的力學性能[7]。

對于載液球殼在剪切流中的變形，相關研究初始是將囊體視為由超彈性膜包裹的液滴，遵循SKALAK R定律[8]。在此基礎上，BARTH[?]S?BIESE L D和RALLISON J M根據黏性應力引起彈性膜隨時間變化的變形方程，研究了自由懸浮在線性剪切流中膠囊的變形[9];POZRIKIDIS C等研究了液體膠囊在剪切流作用下的瞬態變形，討論了變形時彈性膜的失效[10，11];RAMANUJAN S和POZRIKIDIS C通過將彈性膜簡化成彈性球殼進行研究，得到了彈性球殼變形隨剪切速率的變化規律[12];MA J等使用直接數值法研究了球形或扁球形無應力狀態的球殼動態變化，發現球殼變形后呈現相對穩定的外形，加深了人們對微球殼結構的認知[13]。

綜上，已有研究對球殼動力學行為進行了較為系統的分析，但是還缺乏對球殼變形的參數化表征。筆者采用雙向流固耦合方法[14]，綜合考慮幾何與操作參數影響，研究球殼變形規律，為工程應用提供理論參考。

1 三維剪切流中的球殼數值分析模型

1.1 幾何模型及邊界條件

如圖1所示，建立一個由球殼作為固相、流體作為液相的三維模型。球殼具有一定的厚度，懸浮在長方體流體域中心，其內部可以空心，也可以載液。流體域上下各有一塊平板，兩板平行，兩板間充滿有黏不可壓縮的牛頓流體，取流體域尺寸為x=20 mm，y=10 mm，z=10 mm。

流體域上側（y=5 mm）和下側（y=-5 mm）為無速度滑移邊界。當上、下兩平板以相同速度大小、相反的方向持續移動時，由于黏性作用，邊界處的流體與平板同速度流動。流體域前側（z=5 mm）和后側（z=-5 mm）設置為一對周期性邊界條件，左側（x=-10 mm）和右側（x=10 mm）亦設置為周期性邊界條件。當兩平行板以固定速度持續運動時，可產生穩定的三維剪切流場[15]。球殼內部無載液時，球殼外表面與接觸的流體設置為耦合面;若球殼內部有載液，球殼內外表面與接觸的流體均設置為耦合面。

1.2 基本假設及理論模型

模型中，球殼采用各向同性線彈性材料，在建立固體域方程時，作出以下5個基本假設，即連續性假設、均勻性假設、各向同性假設、完全彈性假設、小變形假設。

1.2.1 流體域方程

采用流體連續介質模型，流場的控制方程采用N?S方程，其控制方程可表示為：

+▽·（ρv2-τ）=f （1）

流體域質量守恒方程：

+▽·（ρv）=0?? （2）

式中 f——流體體積力矢量;

t——時間;

v——流體速度矢量;

ρ——流體密度。

τ表示流體剪切力張量，其表達式為：

τ=（-p+μ▽·v）I+2μe??? （3）

e=（▽v+▽vT）

式中 e——速度應力張量;

p——流體壓力;

μ——動力黏度。

本問題中，球殼雷諾數表達式為：

Re=??? （4）

式中 d——球殼的外徑;

U——特征速度，這里取未放置球殼時流場

的截面平均速度。

通過計算得到，雷諾數為1左右，由此可知，流體的慣性力遠小于流體的黏性力，可以忽略。

1.2.2 固體域方程

當球殼受到流體的剪切力時，其結構會發生微小的變形，由于球殼變形后仍保持為連續固體，通過固體幾何控制方程表達發生變形時的連續規律，得到如下方程：

ε

=，

γ

=

+

ε

= ，

γ

=

+

ε

=，

γ

=

+ （5）

式中 ε、γ——球殼上任一點的6個應變。

1.2.3 流固耦合控制方程

在流固耦合交界面處，還應滿足流體與球殼結構應力τ、位移d相等或守恒，即滿足如下2個方程：

τ

·n

=τ

·n

d

=d

（6）

式中 d——流體位移;

d——固體位移;

n——流體單位方向向量;

n——固體單位方向向量;

τ——固體剪切應力。

1.3 網格獨立性驗證

由于雙向流固耦合計算量大，計算周期長，為兼顧模擬效率和模擬精度，對模型進行網格獨立性驗證，結果如圖2所示。當流體域與固體域網格總數從407 534增加到778 526時，空心球殼旋轉速度基本不再變化。同時，在不同的網格數量下進行了質量檢測，證明當網格總數為407 534時，已滿足模擬計算的要求。同此將網格總數為407 534的模型用于后續的模擬。

2 數值模擬方案及結果

2.1 模型參數及評價指標

文中模型參數取值列于表1。

研究球殼變形特性的評價指標較多。研究發現，球殼變形過程中伴隨著球殼的旋轉，采用2個指標表征球殼的變形和旋轉，即時間相關的球殼變形系數和時間相關的球殼旋轉速度。

對于球殼總體變形程度，參照文獻[16]描述外部擾動對固體變形的影響，采用Taylor變形系數D描述其變形，即測量球殼變形最大平面上的最長軸L和最短軸B，其兩軸之差除以兩軸之和，其表達式為：

D=????? （7）

2.2 直徑對球殼變形及旋轉的影響

圖3a是剪切速度0.05 m/s、球殼厚度0.2 mm時，5個不同直徑球殼的變形系數隨時間變化的曲線。由圖3a可知，變形系數隨球殼直徑的增加而增加，1 200步后變形系數趨于穩定。這是因為在0～1 200步內，流場處于逐漸發展階段，變形隨流場剪切力的增加而增大，在1 200步時，流場充分發展，球殼在剪切力的作用下保持相對穩定的變形，變形系數不再改變。圖3b為不同直徑球殼的旋轉速度隨時間變化的曲線。可以發現，球殼直徑對旋轉速度的影響類似于對變形系數的影響，區別在于旋轉速度在1 000步后趨于穩定。

2.3 厚度對球殼變形及旋轉的影響

圖4a為剪切速度0.05 m/s、直徑2.8 mm時，5個不同厚度球殼的變形系數隨時間變化的曲線。從圖4a中可看出，球殼厚度的增加而導致變形系數的減小，變形系數從1 200步開始穩定。球殼厚度增加提高了球殼的強度與穩定性，而剪切力大小未發生變化，因此球殼厚度增加使其變形系數減小。圖4b給出了不同厚度球殼的旋轉速度隨時間的變化規律。由圖4b可以看出，旋轉速度隨球殼厚度的增加而減小，這是因為隨著球殼厚度的增加，球殼自身的轉動慣量增大，故旋轉速度減小。

2.4 剪切速度對球殼變形及旋轉的影響

圖5a是直徑2.4 mm，厚度0.2 mm的空心球殼，在5個不同剪切速度下球殼變形系數隨時間變化的曲線。剪切速度越大，球殼的變形系數越大，剪切速度越小，球殼的變形系數則越小。剪切速度的增加使球殼所在流場的剪切強度增大，導致變形系數隨之增大。不同剪切速度下球殼旋轉速度隨時間的變化曲線如圖5b所示，可見，剪切速度的增大使球殼外耦合面上流速增加，旋轉速度隨之增大。

2.5 載液黏度對球殼變形及旋轉的影響

圖6a是直徑2.4 mm、厚度0.2 mm的載液球殼，在5個不同載液黏度下球殼變形系數隨時間變化的曲線，其中虛線表示同幾何尺寸的空心球殼。由圖6a可知，空心球殼的變形系數高于載液球殼，且載液的黏度越小，變形系數逐漸增大。這是因為載液球殼中載液黏度越大，對球殼的變形抑制作用越強，使得載液球殼的變形系數小于同幾何尺寸的空心球殼。圖6b所示為不同載液黏度下旋轉速度隨時間的變化，顯然，空心球殼的旋轉速度也高于載液球殼。此外，雖然載液黏度的減小導致旋轉速度隨之增大，但增長幅度逐漸減小。三維剪切流中的載液球殼，在變形的同時會發生旋轉，變形后的形狀類似于橢球體，球殼的空間姿態不變，但球殼上的節點圍繞球心持續旋轉。

2.6 球殼中的應力分布

模擬試驗過程中，球殼設置為各向同性線彈性材料，僅發生彈性小變形，所以不考慮彈性失效，直接使用球殼的等效應力對球殼應力分布進行分析。

圖7a、b為球殼直徑2.4 mm、厚度0.2 mm、剪切速度0.05 m/s、空心球殼與載液球殼在流場中穩定時x?y截面的應力分布情況，載液球殼黏度為1.06 kg/（m·s）。從圖7中可知，有無載液的球殼應力分布規律基本一致，但數值不同。結合圖7c可以得出b、d、f、h區域為球殼等效應力最大的區域，而a、c、e、g區域為球殼等效應力最小的區域。

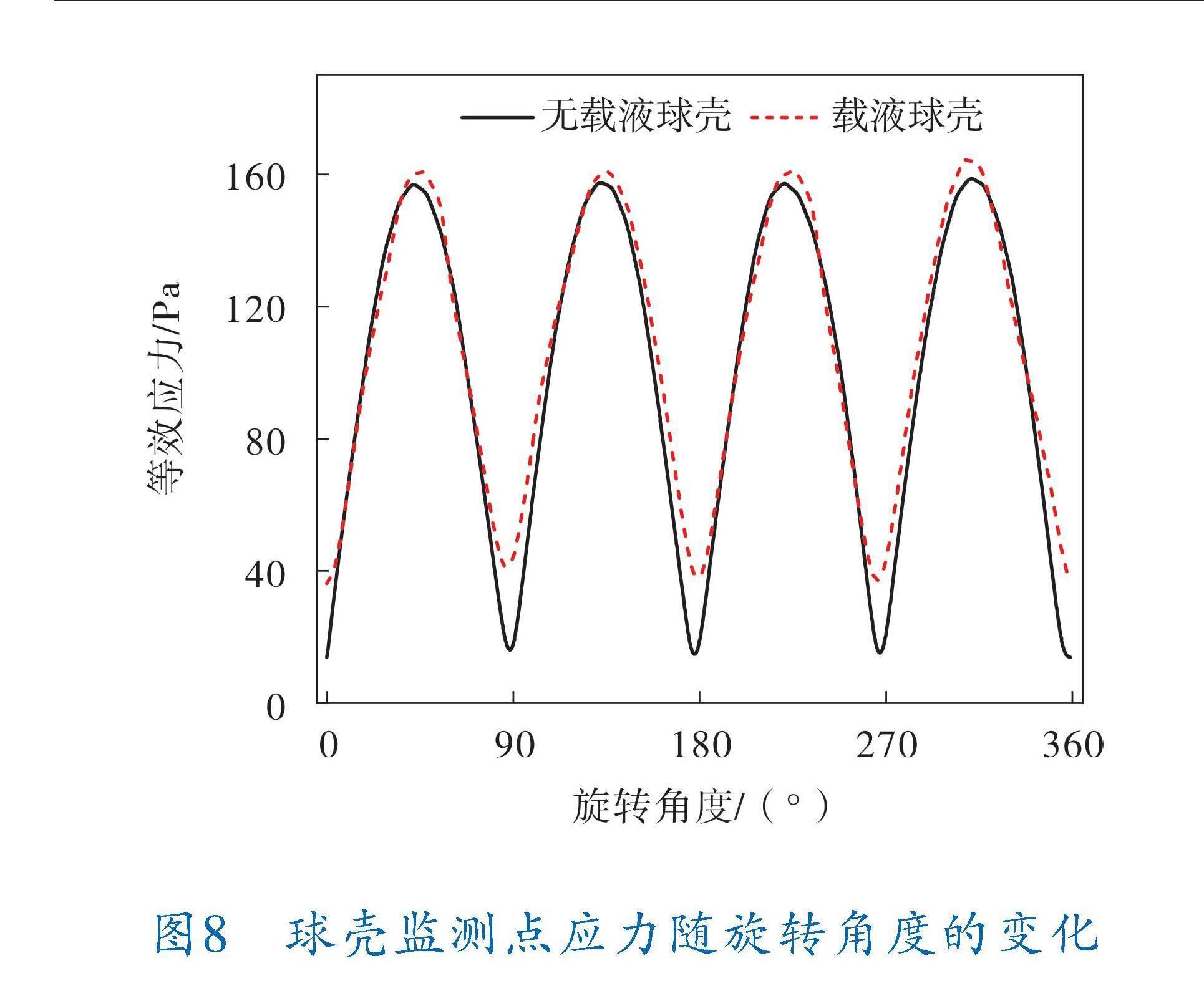
在球殼最上側（?區域）設置一監測點，記錄球殼在穩定流場中旋轉一周內監測點應力的變化，如圖8所示。

由圖8可知，監測點應力隨著球殼旋轉而交替變化，當監測點旋轉至45、135、225、315°時，球殼上應力值最大。空心球殼應力最大值為

159.28 Pa，最小值為12.91 Pa，平均值為100.46 Pa;載液球殼應力最大值為165.65 Pa，應力最小值為34.66 Pa，平均值為104.97 Pa。一個周期內，球殼監測點的應力上升、下降各4次。

材料力學中[17]交變應力的定義為：若構件內某點的應力隨時間發生交替變化，這種應力即為交變應力。由此可得，球殼在剪切流場中會產生交變應力，交變頻率取決于球殼旋轉速度。該工況下空心球殼旋轉速度為5.82 rad/s，即每秒0.93轉，載液球殼旋轉速度為4.91 rad/s，即每秒0.78轉。

綜上所述，空心球殼的交變頻率大于載液球殼，但載液球殼交變應力大于空心球殼，因此，在剪切流環境中使用微球殼時，要特別關注交變應力引起的疲勞[18]。

3 結論

3.1 剪切流場中，球殼的變形系數及旋轉速度會隨剪切速率的增大而增大，流場穩定后，球殼會保持恒定的變形系數和旋轉速度。

3.2 空心球殼的直徑越大，其變形系數及旋轉速度越大;球殼的厚度越大，變形系數及旋轉速度反而減小;剪切速度越大，球殼變形系數及旋轉速度越大。

3.3 同幾何尺寸的空心球殼及載液球殼在同一流場中，空心球殼變形系數及旋轉速度更大;對于載液球殼，載液黏度越大，球殼變形系數及旋轉速度越大，但小于同幾何尺寸的空心球殼;三維剪切流中的載液球殼，在變形的同時會發生旋轉，變形后的形狀類似于橢球體，球殼的空間姿態不變，而球殼上的節點圍繞球心旋轉。

3.4 空心球殼和載液球殼在剪切流場中均會產生交變應力，相較于空心球殼，載液球殼交變應力較大但交變頻率較小。因此，在微球殼結構制備和使用中要關注交變應力引起的疲勞。

參 考 文 獻

[1] GUO Z Y，LIN T，JING D L，et al.A method for real?time mechanical characterisation of mic?rocapsules[J].Biomechanics and Modeling inMechanobiology，2023，22：1209-1220.

[2] LEOP?RCIO B C，MICHELON M，CARVALHO M S.Deformation and rupture of microcapsules flowing through constricted capillary[J].Scientific Reports，2021，11（1）：7707.

[3] SCHMIDT W，F?RTSCH A，LAUMANN M，et al.Oscillating non?progressing flows induce directed cell motion[J].Physical Review Fluids，2022，7（3）：L032201.

[4] QUESADA C，VILLON P，SALSAC A V.Real?time prediction of the deformation of microcapsules using proper orthogonal decomposition[J].Journal of Fluids and Structures，2021，101：103193.

[5] BARTH?S?BIESEL D.Modeling the motion of capsules in flow[J].Current Opinion in Colloid & Interface Science，2011，16（1）：3-12.

[6] POZRIKIDIS C.Effect of membrane bending stiffness on the deformation of capsules in simple shear flow[J].Journal of Fluid Mechanics，2001，440：269-291.

[7] DE LOUBENS C，DESCHAMPS J，GEORGELIN M，et al.Mechanical characterization of cross?linked serum albumin microcapsules[J].Soft Matter，2014，10（25）：4561-4568.

[8] SKALAK R，TOZEREN A，ZARDA R P，et al.Strain en? ergy function of red blood cell membranes[J].Biophysical Journal，1973，13（3）：245-264.

[9] BARTH?S?BIESEL D，RALLISON J M.The time?depe? ndent deformation of a capsule freely suspended in a linear shear flow[J].Journal of Fluid Mechanics，1981， 113：251-267.

[10] POZRIKIDIS C.Finite deformation of liquid capsules enclosed by elastic membranes in simple shear flow[J].Journal of Fluid Mechanics，1995，297：123-152.

[11] ZHOU H，POZRIKIDIS C.Deformation of liquid capsules with incompressible interfaces in simple shear flow[J].Journal of Fluid Mechanics，1995，283：175-200.

[12] RAMANUJAN S，POZRIKIDIS C.Deformation of liquid capsules enclosed by elastic membranes in simple shear flow：large deformations and the effect of fluid viscosities[J].Journal of Fluid Mechanics，1998，361：117-143.

[13] MA J，WANG Z，YOUNG J，et al.An immersed bound ary?lattice Boltzmann method for fluid?structure interaction problems involving viscoelastic fluids and complex geometries[J].Journal of Computational Physics，2020，415：109487.

[14] 俞樹榮，王在剛，劉雪等.波流作用下海洋立管流固耦合動力特性分析[J].化工機械，2013，40（5）：653-657.

[15] 魏慶彩，倪玲英，郭長會，等.SPH方法在剪切流液滴運動規律研究中的應用[J].化工機械，2010，37（3）：308-311.

[16] BARTH?S?BIESEL D.Motion and deformation of elastic capsules and vesicles in flow[J].Annual Review of Fluid Mechanics，2016，48：25-52.

[17] 張濤然，晁曉潔，郭麗紅.材料力學[M].重慶：重慶大學電子音像出版社有限公司，2018：195-197.

[18] 李智慧，王偉華，宋利濱.淋洗塔應力分析與疲勞壽命預測[J].化工機械，2021，48（4）：571-575.

（收稿日期：2023-05-09，修回日期：2024-05-13）