汽車碰撞速度與年齡因素對下肢損傷影響

摘 要：本研究旨在探討年齡因素對行人下肢損傷的影響，以提高行人保護水平?；贑IDAS（China in-depth accident study）數據庫，篩選了2017-2022年的16起真實行人碰撞案例。利用PC-Crash軟件重建事故，獲取邊界條件，并將其導入車輛-行人下肢有限元碰撞模型進行損傷重建。通過邏輯回歸模型分析，得到不同碰撞速度下，各年齡段的損傷參數和下肢損傷風險預測模型。研究結果顯示，各年齡段的下肢長骨損傷閾值和耐受極限存在差異。本研究為行人保護法規及下肢損傷評估指標制定提供了重要數據支撐。

關鍵詞：汽車-行人 年齡-速度 事故重建 AIS3+重傷風險 邏輯回歸 有限元

世界衛生組織《2023年道路安全全球現狀報告》指出，盡管全球道路交通死亡人數每年下降5%，但行人和其他弱勢道路使用者的死亡風險正在上升[1]。據胡林等人研究[2]，下肢損傷在所有AIS2+損傷中占32.6%，在所有傷情中比例為32.8%。下肢損傷雖少致命，但給社會帶來巨大財產損失，因此加強行人下肢保護至關重要。

在行人-車輛碰撞事故中，行人下肢的損傷程度受多種因素影響。研究表明，撞擊時的速度以及行人的年齡是影響行人下肢損傷的最重要因素[3-4]。目前，Klinich等人[4-5]的研究圍繞事故中下肢受損因素對其Abbreviated Injury Scale （AIS）等級的影響，結果表明，隨著碰撞速度的增加、行人年齡的增長以及行人身高或車輛重心位置的上升，行人下肢受到AIS2級及以上損傷的風險也會增加。Kunitomi[6]則致力于模擬行人有限元碰撞仿真分析，探究了不同速度沖擊下的乘用車前端結構變化對行人下肢骨折的效應。行人年齡對下肢損傷有重要影響。隨著年齡增長，下肢承受應力應變減小，更易受損。楊濟匡等人[7]發現，隨著年齡的增長，腿部長骨對拉力和壓力的承受能力有差異，導致骨折的風險隨年齡遞增而上升。Klein等人[8]開發了包含年齡、性別、股骨結構和身體質量指數的股骨有限元模型，模擬行人和車輛碰撞，發現不同年齡段碰撞模型是下肢損傷存在差異。

盡管有很多學者對行人下肢損傷做過研究，但很少有研究考慮到速度、年齡對下肢損傷的綜合影響。本文基于CIDAS數據庫中的16個行人下肢損傷案例，運用PC-Crash事故重建技術，獲取了行人與汽車相撞時的相對速度以及行人相對汽車前部的姿態角度等關鍵邊界條件，將所述邊界條件整合進已構建的車-行人下肢碰撞有限元模型中模擬碰撞，進行損傷重建。通過分析行人下肢損傷參數（如股骨和脛腓骨的彎矩和剪切力），結合邏輯回歸模型，探討了行人年齡、長骨損傷參數與AIS3+重傷風險之間的相關性，并深入研究年齡因素對下肢損傷在不同碰撞速度下的影響[4]。

1 數據模型

在挑選的16起行人下肢損傷案例基礎上，利用PC-Crash事故重建技術獲取關鍵的邊界條件，進行車輛-行人有限元碰撞仿真，獲取行人下肢股骨和脛腓骨損傷參數，并開展行人年齡、長骨損傷參數與AIS3+重傷風險的相關性分析。

1.1 車輛與下肢碰撞模型的建立與驗證

1.1.1 具有年齡特征的行人下肢有限元模型

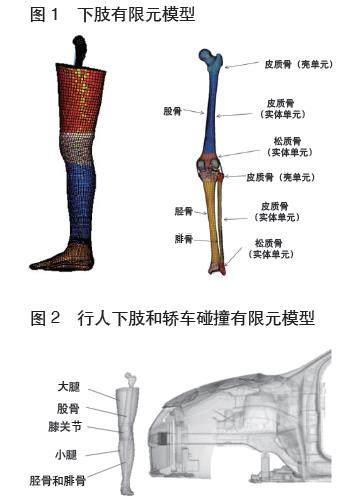
研究表明，年齡是影響行人下肢重傷和長骨骨折風險的關鍵因素[9]。隨著年齡增長，骨骼失效應力減小，耐受極限降低，骨折和重傷風險增加。這主要體現在下肢材料和骨骼結構上。本文采用龍永程[10]建立的下肢有限元模型進行研究。該模型包括皮膚、肌肉、膝關節韌帶和長骨（由股骨、脛骨和腓骨），如圖1。長骨骨干部位的皮層骨與端部的海綿骨在材質屬性上有顯著差異，這是引起長骨骨折的重要原因。本文可根據年齡對下肢有限元模型中膝關節力學性能和骨骼幾何結構的影響對材料參數進行調整[11]。

1.1.2 汽車-行人碰撞模型建立及驗證

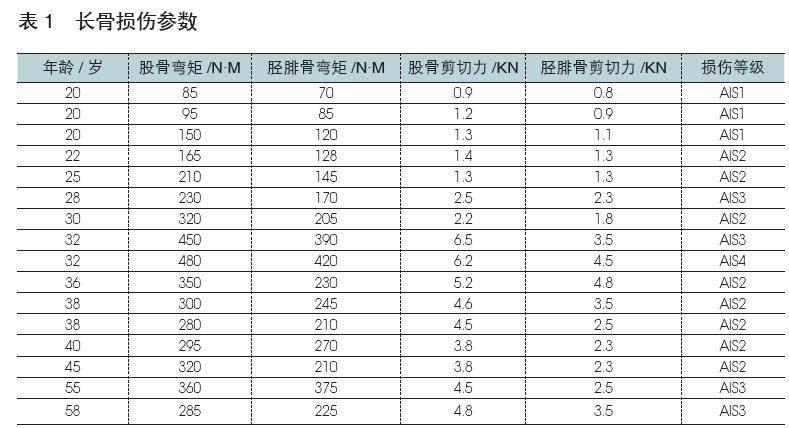
為進一步分析年齡，長骨彎矩和剪切力等損傷參數和AIS3+重傷風險的相關性，驗證有限元模型的有效性。本文將有限元模型中的保險杠距地高度等參數進行調整，車頭數據參照汽車對行人碰撞保護法規方法，將汽車前保險杠距離地面的高度設為540 mm，前保險杠垂直沖擊面的寬度定為120 mm。為降低模擬時間成本，用等效的質量塊代替了車輛A柱之后的區域，在不改變車輛整體重量及其重心位置的基礎上，在車尾部分加上了集中的重量塊，并與后端梁實現了剛性連接[10]，如圖2。

本文所有的真實事故案例均來自CIDAS數據庫，由于每起事故的行人參與方身高體重都不同，本文通過運用Hypermesh軟件內的Hypermorph功能，對行人下肢有限元網格進行調節以適應各個年齡段長骨的尺寸變化，模擬人體自身體重對股骨設置加載力，下肢與地面的摩擦因數為0.65。

選用公式（1）調整下肢模型的高度使之配合標準，以及利用公式（2）進行股骨頭受力的調整。實驗以成年人中位數尺寸為行人標準體型，該體型的標準身高與體重分別為1.75米和78公斤[10-11]。

（1）

式中：H是事故中受害行人的身高，是模型中下肢的實際長度；

H0標準人體模型的身高；是初始模型的下肢長度。

（2）

式中：F是事故中施加在股骨上的力模型，W是被撞行人的重量；

F0是原設定的股骨承受的力，取400N；W0是初始的人體重量。

針對具體案例特征，采用PC-Crash分析工具，對行人下肢與小轎車碰撞案例進行重建，獲取相對碰撞速度等關鍵邊界條件。隨后，將這些參數導入到轎車-行人有限元碰撞仿真模型，進行損傷重建。圖3展示了模型仿真的運動響應，行人下肢首先與轎車保險杠接觸，之后與發動機罩發生碰撞。圖4的對比顯示，模擬撞擊位置與現實汽車受損部位高度一致，證明了該有限元模型在模擬分析中的高仿真性和有效性。

1.2 統計方法

本文采用邏輯回歸的方法來解釋行人年齡、碰撞速度和下肢長骨損傷參數（長骨彎矩和剪切力）與下肢AIS3+重傷和骨折的關系，并且構建邏輯回歸模型：

（3）

其中P為發生概率，x為考察變量，系數α和β為模型中尚待評估的系數，并可以通過最大似然估計的方法來求解，本文根據設定的P值顯著性標準（0.05）來判斷變量間的相關性是否統計上顯著：P值小于0.05表明相關性顯著，否則不顯著[12]。

2 結果分析

2.1 年齡-長骨損傷參數-重傷風險的相關性分析

隨著行人年齡增長，下肢的骨折的極限應變和應力會逐步降低，骨折發生的可能性相應增加[7]。本文依據院門診記錄對行人下肢的損傷描述，利用AIS損傷等級對下肢損傷進行評判，分類為輕傷（AIS0-2級）與重傷（AIS3級及以上）[3-4]?；谡鎸嵃咐?，使用PC-Crash軟件重建關鍵邊界條件，導入車輛-行人下肢有限元碰撞模型進行損傷分析。通過仿真，得到股骨和脛腓骨的彎矩和剪切力等參數，并分析行人年齡-長骨損傷參數-AIS3+重傷風險的相關性。在16起事故案例中，仿真得到股骨和脛腓骨的彎矩和剪切力等損傷參數，如表1所示。

根據仿真導出的數據結果可知，樣本股骨和脛腓骨彎矩平均值分別為273 N·M和3218 N·M，剪切力平均值分別為3.4 KN和2.4 KN。根據樣本數據，利用公式（9）構建了年齡-長骨損傷參數-行人下肢嚴重損傷AIS3+的邏輯回歸方程，其中x為考察變量，系數α、β和為待估計參數，并可以通過最大似然估計的方法來求解，由表2和表3統計數據表明，P值小于0.05，即驗證了長骨（股骨和脛腓骨）損傷參數與下肢嚴重損傷之間存在顯著的相關性。

根據股骨和脛腓骨的彎矩邏輯回歸分析結果，構建了年齡-長骨彎矩-AIS3+重傷風險的三維可視圖，如圖5所示，可以預測在不同年齡和不同長骨彎矩值情況下對AIS3+重傷風險概率進行預測，由圖可見隨著年齡、股骨和脛腓骨彎矩值的變大，下肢重傷風險越來越大，通過圖5（a）和圖5（b）的對比發現在相同年齡條件下，脛腓骨彎矩和股骨彎矩對行人下肢重傷風險的影響存在差異。

當下肢重傷損傷風險概率為50%時，對應的長骨彎矩和年齡分布如圖6所示，隨著年齡變大，長骨彎矩值逐漸變小，當行人年齡為30歲，下肢發生重傷概率為50%時對應行人股骨彎矩值為396 N·M，脛腓骨彎矩值為315 N·M，當行人年齡為50歲，下肢發生重傷概率為50%時對應行人股骨彎矩值為300 N·M，脛腓骨彎矩值為244 N·M，在具有相同重傷風險概率下，股骨彎矩值始終要大于脛腓骨彎矩值。

根據股骨和脛腓骨的剪切力邏輯回歸分析結果，構建了行人年齡-長骨剪切力-AIS3+重傷風險的三維可視圖，如圖7可見隨著年齡、股骨和脛腓骨剪切力值的變大，下肢重傷風險越來越大，通過圖7（a）和圖7（b）的對比發現在相同年齡和剪切力值條件下，脛腓骨剪切力對行人下肢重傷風險的影響要大于股骨剪切力對下肢重傷風險的影響。

當行人下肢重傷風險概率為50%時，其長骨剪切力和年齡分布如圖8，隨著年齡變大，長骨剪切力值逐漸變小，當行人年齡為30歲，下肢發生重傷概率為50%時對應行人股骨剪切力值為5.45 KN，脛腓骨剪切力值為4.25 KN，當行人年齡為50歲，下肢發生重傷概率為50%時對應行人股骨剪切力值為4.2 KN，脛腓骨剪切力值為2.5 KN，在具有相同重傷風險概率時，股骨剪切力值始終要大于脛腓骨剪切力值。

以上數據與Kerrigan等的研究結果一致，他們測得30-50歲人群的股骨彎矩和脛骨彎矩分別為412±102 N·M和310±50 N·M，誤差為6%，誤差在正常范圍內[13]。同時，模擬的結果也與Martens等人[14]記錄的股骨彎曲耐受極限（373±84 N·M）持平。脛腓骨彎矩和剪切力值也符合Nyquist等人[15]試驗測量年齡段為30-50歲時彎矩（317±88 N·M）和剪切力（4.1±1.2） KN的范圍，與試驗測量的脛骨剪切力相比低了13.8%，在正常誤差范圍內。與Kress等人[16]測量出年齡為50歲時股骨彎矩數據（320 N·M）和剪切力數據（3-10 KN）吻合，但脛骨彎矩值與Mo Fuhao等人[17]對年齡為50歲的脛骨骨干測試數據339 N·M相比低了28%，這由于實驗加載位置不同，得出來的數據會有差距，脛骨中段對抗彎曲的能力要優于其近端或遠端1/3區域的能力，另外本研究模型簡化了膝蓋的韌帶復雜結構，這個做法也降低了模型的生物仿真性，并可能進一步影響到了實驗結果的信準度。針對這一點，未來的相關研究需提高對生物仿真性的要求[4]。

3 結語

本文以CIDAS數據庫記錄的16起案例為研究基礎，利用PC-Crash軟件和車輛-行人下肢有限元碰撞模型，建立行人年齡-長骨損傷參數-AIS3+重傷風險的三維可視圖，可得出結論：

由對應的長骨彎矩和剪切力與年齡分布圖可以發現，當下肢重傷損傷風險概率為50%時，行人年齡為30歲，對應行人股骨彎矩值為396 N·m，脛腓骨彎矩值為315 N·m，對應行人股骨剪切力值為5.45 KN，脛腓骨剪切力值為4.25 KN；行人年齡為50歲，對應行人股骨彎矩值為300 N·M，脛腓骨彎矩值為244 N·M，對應行人股骨剪切力值為4.2 KN，脛腓骨剪切力值為2.5 KN，不同年齡段脛腓骨和股骨的彎矩和剪切力值對行人下肢重傷風險的影響存在差異。

基金項目：湖南省教育廳資助科研項目（22C1083），工程車輛安全性設計與可靠性技術湖南省重點實驗室（長沙理工大學）開放基金資助項目（2020YB05）資助。

參考文獻：

[1] WHO. Global status report on road safety 2023[EB/OL].https：//www.who.int/teams/social-determinants-of-health/safety-and-mobility/global-status-report-on-road-safety-2023.

[2] Jing Huang， Yang Peng， Lin Hu. A multilayer stacking method base on RFE-SHAP feature selection strategy for recognition of drivers mental load and emotional state. Expert Systems with Applications， 2024， 238： 121729.

[3]陳凱.行人年齡和碰撞速度對行人下肢損傷的影響研究[D].長沙：長沙理工大學，2019.

CHEN K. Effects of Pedestrian Age and Collision Speed on Pedestrian Lower Limb Injury[D]. Changsha： Changsha University of Science & Technology， 2019.

[4]胡林，陳凱，黃晶，等.年齡因素對行人下肢損傷的影響研究[J].機械工程學報，2020，56（02）：106-120.

HU L， CHEN K， HUANG J， et al. Study on the Effect of Age on the Lower Extremity Injury of Pedestrians[J]. Journal of Mechanical Engineering， 2020，56（02）：106-120.

[5] K D Klinich，L W Schneider. Bio-mechanics of Pedestrian Injuries Related to Lower Extremity Injury Assessment Tools： A Review of the Literature and Analysis of Pedestrian Crash Database [D]. Michigan： University of Michigan Transportation Research Institute， 2003.

[6] Kunitomi S， Yamamoto Y， Kato R， et al. The Development of the Lower Extremity of a Human Fe Model and the Influence of Anatomical Detailed Modelling in Vehicle-to-pedestrian Impacts[J]// International Research Council on Biomechanics of Injury（IRCOBI）. Antwerp， Belgium：2017 IRCOBI Conference Proceedings， Oct 21 2017， 17-62.

[7] Yang J. Review of injury biomechanics in car-pedestrian collisions[J]. International journal of vehicle safety， 2005， 1（1）： 100-117.

[8] Klein K F， Hu J， Reed M P， et al. Validation of a Parametric Finite Element Human Femur Model[J]. Traffic Injury Prevention， 2017， 18（4）：420-426.

[9]王丙雨，聶進，DIETMAROTTE，等.碰撞速度和行人年齡對下肢嚴重損傷風險的影響[J].汽車安全與節能學報，2018，9（1）：25-31.

[10]龍永程.年齡因素對行人下肢有限元建模及損傷的影響研究[D].長沙：湖南大學，2016.

[11] Weaver A A， Schoell S L， Nguyen C M， et al. Morphometric Analysis of Variation in the Sternum with Sex and Age[J]. Journal of Morphology， 2014， 275（11）： 1284-1299.

[12] Kulas J T， Roji R G P P， Smith A M. IBM SPSS Essentials： Managing and Analyzing Social Sciences Data[M]. John Wiley & Sons， 2021.

[13] Kerrigan J R， Bhalla K S， Madeley N J， et al. Experiments for establishing pedestrian-impact lower limb injury criteria[C]. //SAE 2003 World Congress （SP-1740）. 2004.

[14] Martens M， Van A R， De M P， et al. Mechanical behaviour of femoral bones in bending loading[J]. Journal of Biomechanics， 1986， 19（6）： 443-454.

[15] Nyquist G W. Facial Impact Tolerance and Response[C]// Proc. of the， Stapp Car Crash Conference. 1986：3-11.

[16] Kress T A， Snider J N， Porta D J， et al. Human Femur Response to Impact Loading[C]//Proceedings of the International Research Council on the Biomechanics of Injury conference. International Research Council on Biomechanics of Injury， 1993， 21： 93-104.

[17] Mo F， Arnoux P J， Jure J J， et al. Injury tolerance of tibia for the car–pedestrian impact[J]. Accident Analysis & Prevention， 2012， 46： 18-25.