基于自適應蜣螂算法的無人機三維路徑規劃方法

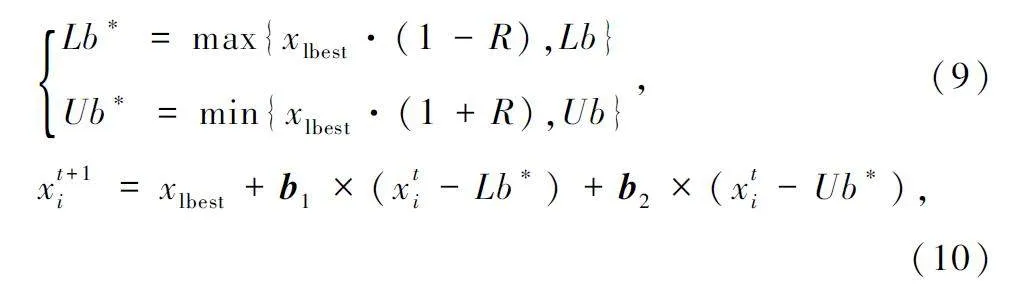
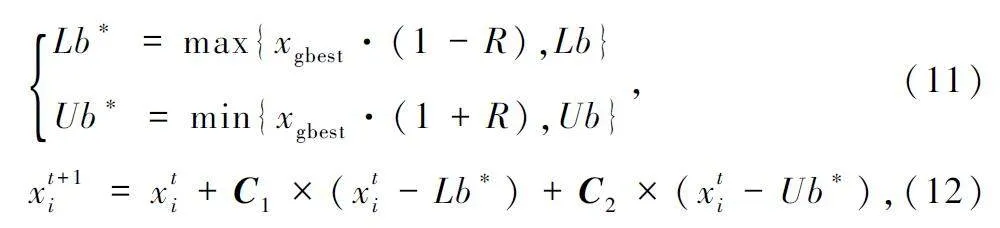
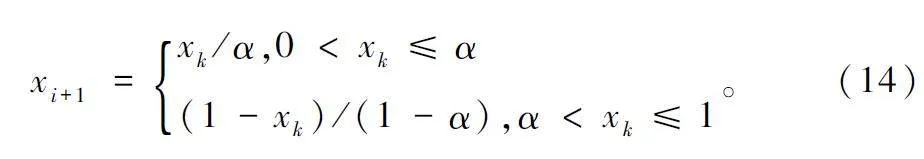
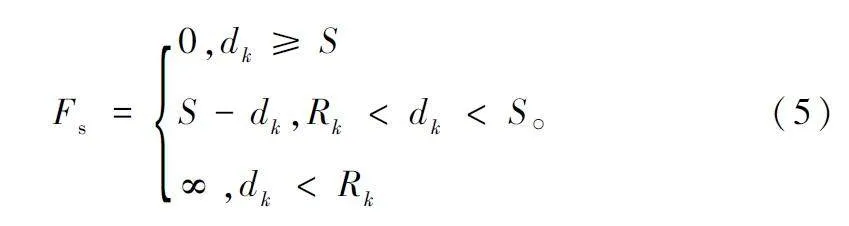
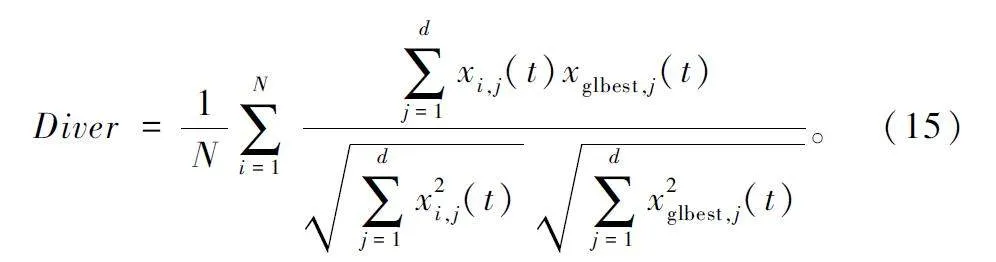
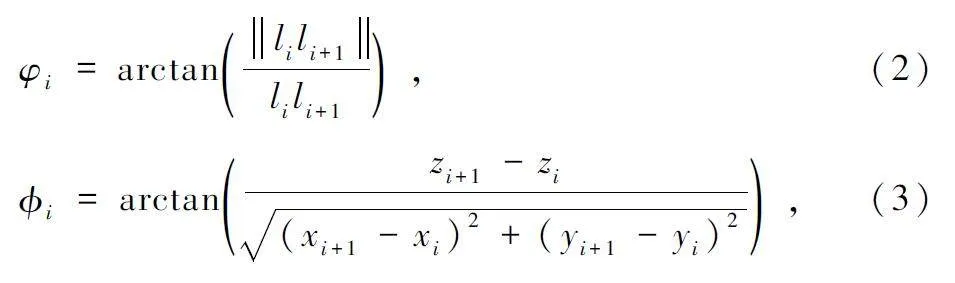
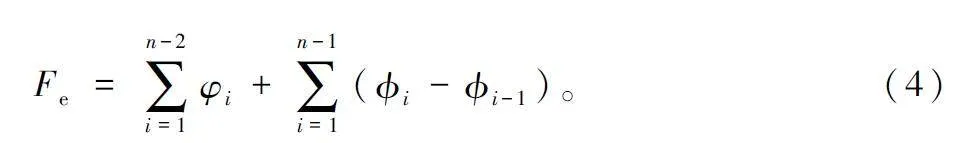
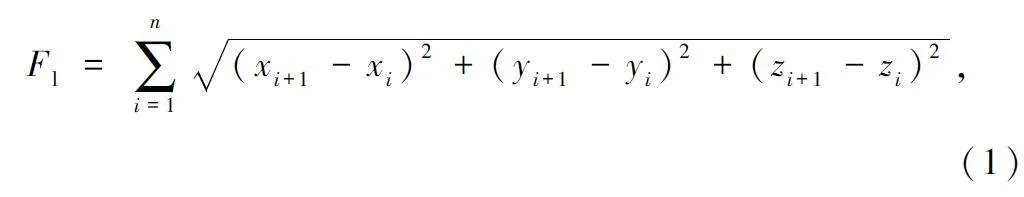
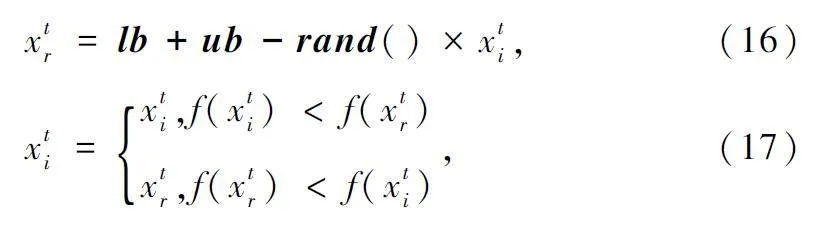
摘 要：山區地勢具有陡峭、溝深壑大的環境特點，導致基于啟發式算法的山區無人機路徑規劃速度慢、質量差，針對該問題提出了基于自適應動作策略蜣螂算法的路徑規劃方法。以路徑長度、飛行安全性以及路徑平滑度構建路徑規劃目標函數；在蜣螂算法中引入種群相似性動作變異策略和反向學習策略，平衡局部優化和全局優化能力；通過對比麻雀算法、蜣螂算法和灰狼算法在１２ 個基準函數上的算法性能，結果表明所提方法具有更快的收斂速度、不易陷入局部最優。山區路徑規劃仿真實驗表明，所提方法比蜣螂算法的路徑規劃質量提高了３７． ６６％ 。

關鍵詞：路徑規劃；蜣螂算法；反向學習；自適應動作策略

中圖分類號：ＴＰ２４２；ＴＰ１８ 文獻標志碼：Ａ 開放科學（資源服務）標識碼（ＯＳＩＤ）：

文章編號：１００３－３１０６（２０２４）０４－０９２８－０９

０ 引言

山區地形的復雜性、起伏高差較大和交通不便等特點常常導致部分區域難以通過傳統方式進行探測、巡視和物資配送等工作，而無人機憑借其機動靈活的優勢在山區得到廣泛應用，因此在山區復雜環境下，高質量、快速地規劃飛行路徑對提高無人機任務效率具有重要意義［１－２］。

面向無人機三維路徑規劃問題，許多學者基于啟發式算法展開了豐富的研究。藺文軒等［３］針對三維路徑規劃問題，在粒子群算法中引入分組優化策略，并在小組粒子優化時采取模擬退火操作，有效避免了陷入局部最優和收斂慢的缺點。蘇菲［４］在傳統蝙蝠算法中引入黃金正弦算法，對最優個體進行全維和單維搜索，提高了收斂速度。黃鶴等［５］在飛蛾撲火算法中引入交叉算子和高斯變異算子，增強了全局搜索能力并提高了算法尋優精度。巫茜等［６］提出了改進信息素更新規則的蟻群算法并引入航跡導航因子，一定程度上克服了山區影響，避免路徑陷入局部最優。郭啟程等［７］在鯨魚優化算法中加入萊維飛行進行隨機擾動，并引入信息交流機制平衡搜索能力，提高收斂精度和速度。Ｚｅｎｇ 等［８］基于距離動態鄰域設計粒子群算法速度更新機制并與差分進化算法進行融合以緩解過早收斂，增強搜索能力。段建民等［９］將遺傳算法和改進的人工勢場模型結合并行搜索，利用人工勢場法優化遺傳算法全局路徑，增強跳出局部最優的能力。許諾［１０］將粒子群算法與遺傳算法結合，設置動態慣性權重并引入步長因子平衡局部和全局搜索。

上述方法在一定程度上提升了規劃路徑的質量和算法的收斂速度，但是面向山區陡峭地勢的復雜環境，仍存在路徑規劃效果差的問題。因此，本文分析無人機運動約束條件和路徑規劃要求，構建了山區環境中三維路徑規劃問題模型；結合蜣螂算法位置更新策略多的優勢，引入反向學習策略和種群相似性變異策略，提出自適應變異蜣螂算法（ＡｄａｐｔｉｖｅＭｕｔａｔｉｏｎ Ｄｕｎｇ Ｂｅｅｔｌｅ Ａｌｇｏｒｉｔｈｍ，ＡＭＤＢＯ）使得在進行山區路徑規劃時蜣螂能自適應地選擇動作，從而有效跳出局部最優，獲得高質量路徑。

１ 無人機三維路徑規劃目標函數

無人機三維路徑規劃問題屬于優化問題，本文從路徑長度、路徑平滑度和飛行安全度方面構建路徑規劃目標函數。

① 路徑長度

路徑長度是判斷路徑質量的重要依據，路徑長度越短，越有利于無人機節省能耗［１１］。因此路徑長度為：

式中：ｎ 為航跡點數目，（ｘｉ，ｙｉ，ｚｉ）為第ｉ 個航跡點的位置。

② 路徑平滑度

規劃路徑應盡量減少大角度偏航和高度的突變，需要保持路徑平滑。由于山區陡峭、落差大的地形特點，無人機在山區飛行需要飛行路徑滿足自身最大爬升角和爬升率的要求［１２］。ｌｉ 表示２ 個航跡點之間的距離，式（２）和式（３）分別表示偏轉角φｉ 和俯仰角ｉ，路徑平滑度成本函數定義為式（４）。

③ 飛行安全性

路徑規劃中的路徑還必須要確保無人機的安全運行，因此引入飛行安全性能夠引導無人機躲避環境中的障礙物［１３］。如圖１ 所示，空域內存在中心坐標為Ｏｋ，半徑為Ｒｋ 的障礙物ｋ，無人機的飛行節點與障礙物的垂線距離ｄｋ 應該大于安全距離閾值Ｓ，即無人機必須限定在陰影之外的區域飛行，才能確保飛行的安全，飛行安全性的計算如下：

對上述各類成本函數進行加權綜合，構成多目標路徑規劃問題的目標函數Ｆ：

Ｆ ＝ ω１ Ｆｌ ＋ ω２ Ｆｅ ＋ ω３ Ｆｓ ， （６）

式中：Ｆｌ、Ｆｅ、Ｆｓ 依次為上述３ 種代價函數，ω１ 、ω２ 、ω３ 分別為路徑長度、航跡平滑度和飛行安全性的權重系數。目標函數值越小代表路徑質量就越好。

２ 蜣螂優化算法

２． １ 原始蜣螂算法

蜣螂優化算法（Ｄｕｎｇ Ｂｅｅｔｌｅ Ｏｐｔｉｍｉｚｅｒ Ａｌｇｏｒｉｔｈｍ，ＤＢＯ）是一種新穎的群體智能算法，通過模擬蜣螂的滾球、繁殖、覓食和偷竊４ 個動作行為進行位置更新和優化，每種策略側重的方向有所不同［１４］。蜣螂算法的多樣化位置更新策略可以更加全面地探索搜索空間，在實際應用中能夠有效地解決復雜的搜索和優化問題。

① 滾球行為

蜣螂滾球行為分為有障礙模式和無障礙模式。當無障礙時，光源的強度會影響蜣螂的位置，蜣螂在滾球行為過程中位置更新如式（７）所示；當遇到障礙物無法前進時，通過使用切線函數來模擬跳舞行為，位置更新如式（８）所示。

ｘｔ＋１ｉ ＝ ｘｔｉ＋ λ·ｋ·ｘｔ－１ｉ ＋ ｂ· ｘｔｉ－ ｘｗｏｒｓｔ ， （７）

ｘｔ＋１ｉ ＝ ｘｔｉ＋ ｔａｎ（θ） ｘｔｉ－ ｘｔ－１ｉ ， （８）

式中：ｘｔｉ為ｔ 次迭代時第ｉ 個個體的位置，λ 模擬自然因素隨機取－１ 或１，ｋ 為［０，１］的隨機偏轉系數，ｂ為隨機系數，ｘｗｏｒｓｔ 為最差個體位置。

② 繁殖行為

利用邊界選擇策略來模擬蜣螂產卵的安全區域，如式（９）所示；確定產卵區域后，雛球的位置隨產卵區域進行動態變化，如式（１０）所示。

式中：ｘｌｂｅｓｔ 為局部最優解，Ｒ ＝ １－ ｔ／ｔｍａｘ，ｔｍａｘ 為最大迭代次數，ｔ 為當前迭代次數；Ｌｂ 為下界，Ｕｂ 為上界，ｂ１ 、ｂ２ 為２ 個Ｄ 維獨立隨機向量。

③ 覓食行為

覓食區域同樣利用邊界選擇策略來動態模擬，如式（１１）所示。覓食蜣螂會在局部范圍內進行覓食行為，蜣螂的位置更新如式（１２）所示。

式中：ｘｇｂｅｓｔ 為全局最優解，Ｃ１ 為服從正態分布的Ｄ維隨機向量，Ｃ２ 為［０，１］的Ｄ 維隨機向量。

④ 偷竊行為

最佳食物來源則是最適合競爭食物的地方，偷竊蜣螂的位置更新如下：

ｘｔ＋１ｉ ＝ ｘｇｂｅｓｔ ＋ Ｓ × ｇ × （ ｘｔｉ－ ｘｇｂｅｓｔ ＋ ｘｔｉ－ ｘｌｂｅｓｔ ），（１３）

式中：Ｓ 為常數，ｇ 為服從正態分布的Ｄ 維隨機向量。

從４ 種個體行為的位置更新公式可知，只有滾球行為在算法各時期都具有較好的全局搜索能力；覓食行為在自身位置附近根據動態上下界范圍進行搜索，動態上下界會越來越小，使得覓食行為隨著迭代次數的增加從全局搜索變為局部搜索；繁殖行為和偷竊行為則是在最佳個體的附近根據動態上下界范圍進行局部搜索。

２． ２ 自適應蜣螂算法

２． ２． １ 混沌序列初始化種群

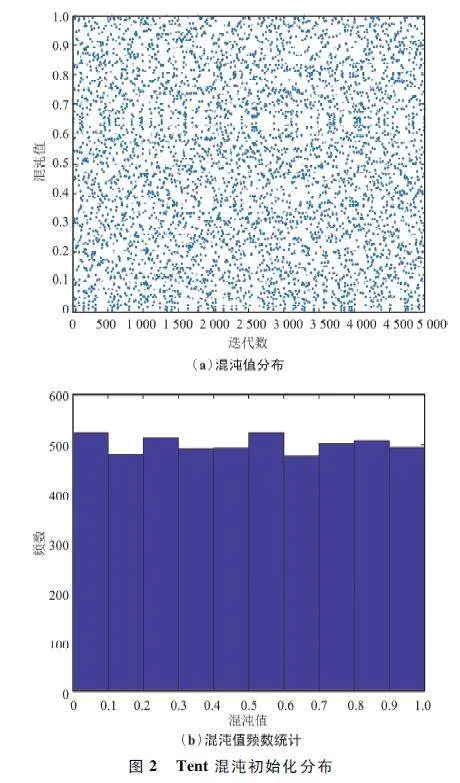
在處理復雜的優化問題時，原始蜣螂算法采用隨機生成種群的方法進行種群初始化，可能會導致種群多樣性低、種群分布不均勻和快速收斂到局部最優解等問題。Ｔｅｎｔ 混沌映射可以生成均勻遍布解空間和相關性較強的初始種群［１５］，因此本文引入Ｔｅｎｔ 混沌映射作為改善蜣螂算法初始化種群多樣性的方法，從而提高智能算法的求解精度和收斂速度。Ｔｅｎｔ 混沌映射公式如下所示：

對ｘ０ 賦初值，經過循環迭代，可以得到［０，１］的隨機序列，該序列具有良好的統計特性，通常用于生成算法的初解，以增加物種的多樣性。當控制參數α ＝０． ４５ 時，初始總體（一維）分布如圖２ 所示。

蜣螂種群初始化過程如下：先隨機生成一個［０，１］的Ｄ 維向量作為初始混沌序列；然后將Ｄ 維向量的每一維數值依次帶入式（１４）計算生成一個新的Ｄ 維向量作為第２ 個混沌序列，重復上述步驟，直到生成Ｎ 個混沌序列；最后將全部混沌序列映射到種群個體的取值范圍內，生成Ｔｅｎｔ 混沌初始化蜣螂種群。

２． ２． ２ 自適應的蜣螂行為變異策略

針對原始蜣螂算法４ 種動作行為的分配比例不均勻，且每個個體只能進行一種動作行為，可能會導致對解空間的搜索不充分或收斂速度慢的問題，本文提出了基于種群相似性的蜣螂動作變異策略和反向學習策略。

① 基于種群相似性的蜣螂動作變異策略

為了使每個蜣螂都能執行４ 種動作行為，本文用迭代次數模擬時間變化，每隔Ｍ 次迭代進行一次蜣螂的動作變異，將當前動作行為變異為下一種行為策略。本文利用余弦相似度來衡量種群相似性，種群多樣性表示如下：

當Ｄｉｖｅｒ 大于０． ５ 時，種群多樣性過低，可能會陷入局部最優，而滾球蜣螂和覓食蜣螂的數量決定了算法對解空間的探索能力和收斂速度。因此將執行繁殖和覓食行為的個體變異為執行滾球行為的個體，增強算法的全局搜索能力以增強物種多樣性，找到新的最佳個體或達到變異個體迭代閾值Ｔｍａｘ 后將變異個體重新恢復為原來的行為個體繼續搜索。

② 反向學習策略

由于繁殖和偷竊行為的全局搜索能力會隨著迭代次數的增加而下降，而反向學習策略［１６］的思想主要是通過生成當前可行解的反向解，并將反向解與原解進行適應度比較選出更好的解，本文利用反向學習策略增強繁殖和偷竊行為的全局搜索能力：

式中：ｘｔｒ 為反向解，ｌｂ 和ｕｂ 為Ｄ 維向量表示每一維的下界和上界，ｒａｎｄ（）為Ｄ 維隨機向量，ｘｔｉ為當前可行解。

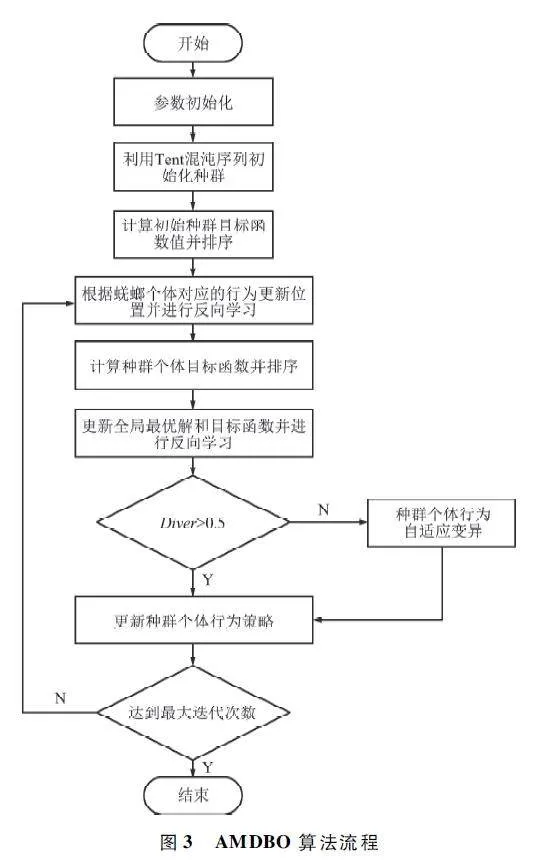
綜上所述，ＡＭＤＢＯ 算法流程如圖３ 所示。

３ 仿真實驗與分析

本文的仿真實驗分為兩部分：① 在ＣＥＣ２０１７中選擇具有不同特征的基準函數［１７］，對比不同算法最優解的搜索速度和搜索質量，驗證ＡＭＤＢＯ 算法的收斂性能、是否具備跳出局部最優的能力；② 構建山區路徑規劃環境，對比不同算法路徑搜索速度和路徑質量，驗證ＡＭＤＢＯ 算法在復雜山區環境是否仍具有較快的收斂速度和尋優能力。

３． １ 基于多樣性基準函數的算法性能分析

為了驗證ＡＭＤＢＯ 算法的尋優性能，本文選取ＤＢＯ、改進灰狼算法（Ｉｍｐｒｏｖｅｄ Ｇｒｅｙ Ｗｏｌｆ ＯｐｔｉｍｉｚｅｒＡｌｇｏｒｉｔｈｍ，ＩＧＷＯ）和麻雀搜索算法（Ｓｐａｒｒｏｗ ＳｅａｒｃｈＡｌｇｏｒｉｔｈｍ，ＳＳＡ）在ＣＥＣ２０１７ 中的１２ 個具有不同特征的基準函數上進行算法性能的對比分析。其中，選擇５ 個單峰基準函數（Ｆ１ ～ Ｆ５ ）分析各算法的單目標求解能力，選擇４ 個多峰基準函數（Ｆ６ ～ Ｆ９ ）和３ 個混合基準函數（Ｆ１０ ～ Ｆ１２ ）分析算法能否跳出局部最優。測試函數具體信息如表１ 所示。

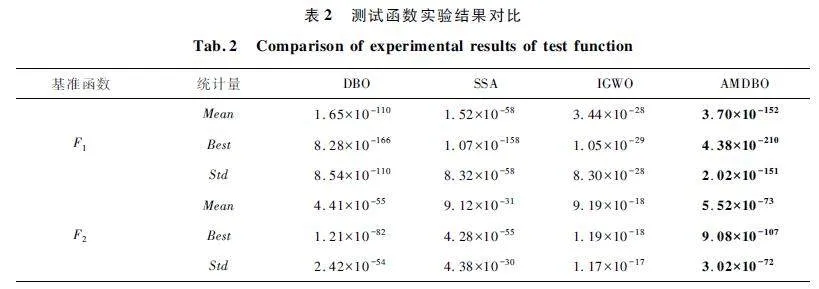
為了提高測試結果的可靠性，降低啟發式算法隨機性的影響，本文將所有算法的種群大小和迭代次數分別設置為３０ 和５００，對每個基準函數都運行３０ 次［１８］，得到３０ 次獨立運行下的最優值（該最優值指的是本次運行下取得的目標函數最優值），并統計出平均值（Ｍｅａｎ）、最佳值（Ｂｅｓｔ）和標準差（Ｓｔｄ），統計對象為３０ 次獨立運行下的最優值結果。平均值表現的是算法對該目標函數的平均的優化能力；最佳值表現的是３０ 次算法運行中對目標函數的最佳優化效果；標準差表現的是算法在該目標函數上優化能力的穩定性。４ 種優化算法對１２ 個基準函數的測試結果對比如表２ 所示。

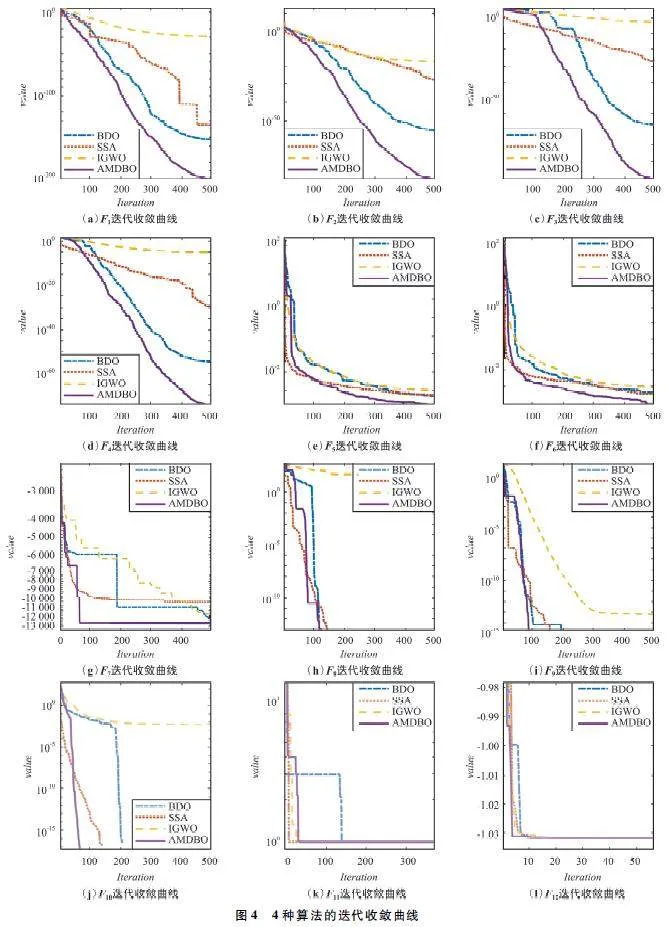
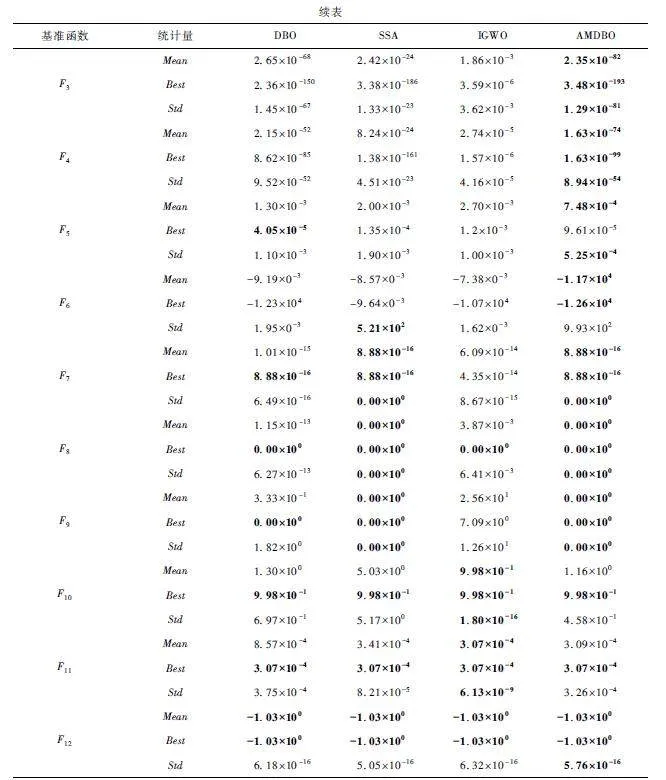
在５ 個單峰基準函數（Ｆ１ ～ Ｆ５ ）測試中，ＡＭＤＢＯ在Ｆ１ ～ Ｆ４ 基準函數上的Ｍｅａｎ、Ｓｔｄ 和Ｂｅｓｔ 均優于其他３ 種算法。對比Ｆ５ 基準函數下Ｍｅａｎ、Ｓｔｄ 和Ｂｅｓｔ的具體數值比較可知：ＤＢＯ 的Ｂｅｓｔ 比ＡＭＤＢＯ 的Ｂｅｓｔ僅高５７． ７６％ ，但是ＡＭＤＢＯ 的Ｍｅａｎ、Ｓｔｄ 分別比ＤＢＯ的值高了７３． ８０％ 和１０９． ５２％ 。綜合Ｆ１ ～ Ｆ５ 的整體表現，ＡＭＤＢＯ 的整體性能優于其他３ 種算法。

在４ 個多峰基準函數（Ｆ６ ～ Ｆ９ ）測試中，ＡＭＤＢＯ的Ｍｅａｎ 和Ｂｅｓｔ 均獲得了第一且精度高于ＤＢＯ 和ＩＧＷＯ；ＡＭＤＢＯ 的Ｓｔｄ 除了在Ｆ６ 上略低于ＳＳＡ，在其他多峰基準函數上都遠遠優于ＩＧＷＯ 和ＤＢＯ。

在３ 個混合基準函數（Ｆ１０ ～ Ｆ１２ ）的測試中，４ 種算法的Ｂｅｓｔ 均能取得理論最優解；ＡＭＤＢＯ 的Ｍｅａｎ和Ｓｔｄ 在Ｆ１０ 和Ｆ１１ 上略低于ＩＧＷＯ，但也都優于ＳＳＡ 和ＤＢＯ；在混合基準函數Ｆ１２ 上，４ 種算法都能得到理論最優的Ｍｅａｎ 和Ｂｅｓｔ，但ＡＭＤＢＯ 的Ｓｔｄ 優于其他３ 種算法。雖然其他算法的Ｍｅａｎ 和Ｂｅｓｔ 都能達到理論最優值，但是ＡＭＤＢＯ 的收斂速度更快、迭代次數更少。圖４（ｊ）～ 圖４（ｌ）為混合基準函數（Ｆ１０ ～ Ｆ１２ ）測試的收斂曲線，ＡＭＤＢＯ 的收斂速度僅次于ＳＳＡ，優于ＤＢＯ 和ＩＧＷＯ。

綜合上述測試，在３ 類基準函數上ＡＭＤＢＯ 的Ｍｅａｎ 和Ｂｅｓｔ 大部分優于其他３ 種算法；在收斂到相同精度的結果時，ＡＭＤＢＯ 所用的迭代次數也更低。ＤＢＯ 性能略差于ＡＭＤＢＯ，但是大部分測試結果相比ＳＳＡ 和ＩＧＷＯ 較優或齊平。

３． ２ 面向山區三維路徑規劃分析。

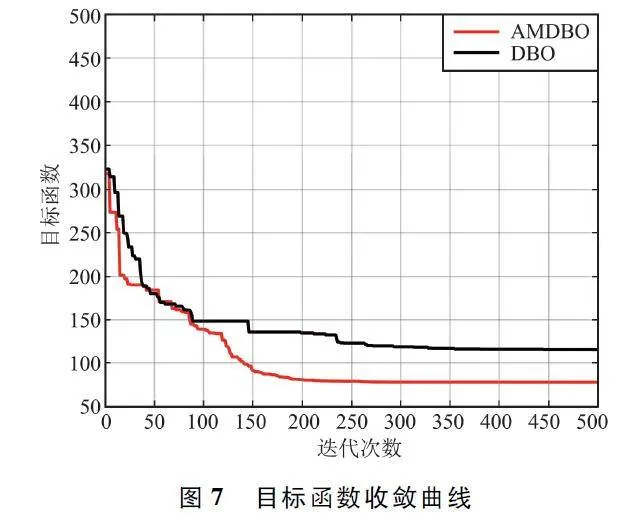
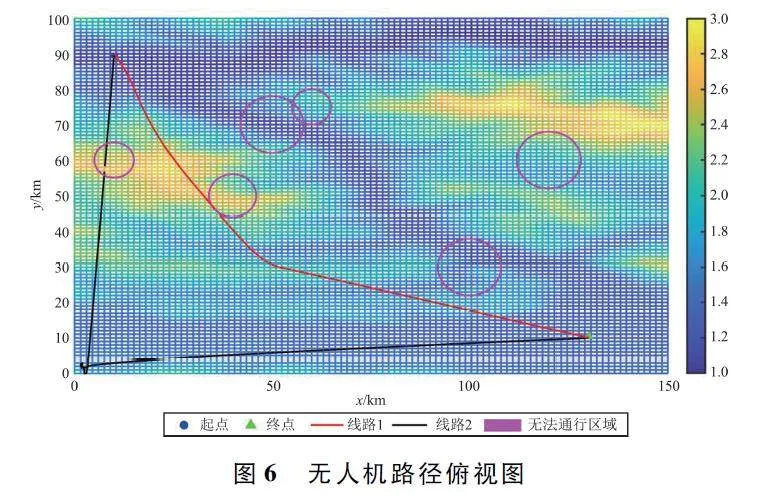
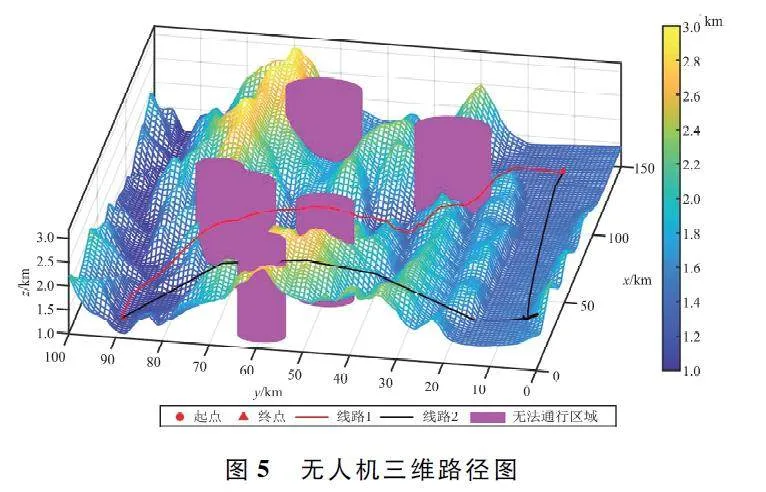
讀取某一山區環境的數字高程模型地圖，該地區最大高度落差超過２ ｋｍ，地勢起伏劇烈分布溝壑眾多，在該地形中隨機生成環境擾動如圖５ 所示（粉色圓柱）。設置無人機的起點和終點分別為（１０，９０，１． １１５）和（１３０，１０，１． ３６７），單位為ｋｍ。由３． １ 中的算法性能實驗可知ＤＢＯ 與ＳＳＡ、ＩＧＷＯ 相比，性能更優，因此路徑規劃實驗中選取ＤＢＯ 與ＡＭＤＢＯ 進行對比。算法中種群個體數量統一為３０，最大迭代次數為５００。基于ＡＭＤＢＯ 和ＤＢＯ 生成的路徑如圖５ 和圖６ 所示，圖中，線路１ 為ＡＭＤＢＯ 算法路徑規劃結果，線路２ 為ＤＢＯ 算法路徑規劃結果。

對比ＤＢＯ 和ＡＭＤＢＯ 的飛行路徑可以看出，原始ＤＢＯ 在進行迭代時陷入了局部最優，且飛行路徑長沒有規避環境擾動，飛行高度低沒有保障離地安全高度；而ＡＭＤＢＯ 算法的飛行路徑平滑，有效規避了環境擾動并且保障了與障礙物之間的距離和離地安全高度。

目標函數收斂曲線如圖７ 所示。可以看出，原始ＤＢＯ 的收斂較慢，在２５０ 次迭代之后逐漸開始收斂。本文算法在開始時能夠快速地持續搜索，在２００ 次迭代之后逐漸收斂，且收斂值低于ＤＢＯ，結果表明ＤＢＯ 在迭代次數達到９５ 和１５０ 時都陷入了局部最優，驗證了ＡＭＤＢＯ 具備跳出局部最優的能力。

綜合各類表現看，本文算法具有更快的收斂速度且能快速跳出局部最優解，能夠在山區復雜環境中規劃出較高質量的路徑。

４ 結束語

受山區環境影響，基于啟發式算法的路徑規劃易陷入局部最優且收斂速度慢，本文在蜣螂算法進行初始化時引入混沌初始化使得種群分布更均勻，有效提高了種群多樣性；構建了種群相似性動作變異策略和反向學習策略，平衡局部優化和全局優化能力。對基于多個基準函數的尋優能力進行對比分析，結果表明ＡＭＤＢＯ 相比ＤＢＯ、ＳＳＡ、ＩＧＷＯ 具有更好的求解速度和精度；山區環境中的路徑規劃結果表明ＡＭＤＢＯ 比ＤＢＯ 收斂更快，能較快地跳出局部最優，路徑質量更高。下一步研究將考慮如何提升山區多目標點的路徑規劃質量。

參考文獻

［１］ 路晶，史宇，張書暢，等． 無人機航跡規劃算法綜述［Ｊ］． 航空計算技術，２０２２，５２（４）：１３１－１３４．

［２］ 雷耀麟，丁文銳，李雅，等． 群體智能支撐的無人機群航路規劃應用綜述［Ｊ］． 無線電工程，２０２３，５３ （７）：１５０９－１５１９．

［３］ 藺文軒，謝文俊，張鵬，等． 基于分組優化改進粒子群算法的無人機三維路徑規劃［Ｊ］． 火力與指揮控制，２０２３，４８（１）：２０－２５．

［４］ 蘇菲． 基于改進蝙蝠算法的無人機三維路徑規劃［Ｊ］．無線電工程，２０２２，５２（１２）：２２２９－２２３６．

［５］ 黃鶴，吳琨，王會峰，等． 基于改進飛蛾撲火算法的無人機低空突防路徑規劃［Ｊ］． 中國慣性技術學報，２０２１，２９（２）：２５６－２６３．

［６］ 巫茜，黃浩，曾青，等． 改進ＡＣＯ 算法的ＵＡＶ 航跡規劃在山區物流配送中的應用研究［Ｊ］． 重慶理工大學學報（自然科學），２０２２，３６（１０）：１８５－１９１．

［７］ 郭啟程，杜曉玉，張延宇，等． 基于改進鯨魚算法的無人機三維路徑規劃［Ｊ］． 計算機科學，２０２１，４８ （１２）：３０４－３１１．

［８］ ＺＥＮＧ Ｎ Ｙ，ＷＡＮＧ Ｚ Ｄ，ＬＩＵ Ｗ Ｂ，ｅｔ ａｌ． Ａ Ｄｙｎａｍｉｃ Ｎｅｉｇｈｂｏｒｈｏｏｄｂａｓｅｄ Ｓｗｉｔｃｈｉｎｇ Ｐａｒｔｉｃｌｅ Ｓｗａｒｍ Ｏｐｔｉｍｉｚａｔｉｏｎ Ａｌｇｏｒｉｔｈｍ ［Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｃｙｂｅｒｎｅｔｉｃｓ，２０２２，５２（９）：９２９０－９３０１．

［９］ 段建民，陳強龍． 基于改進人工勢場－遺傳算法的路徑規劃算法研究［Ｊ］． 國外電子測量技術，２０１９，３８（３）：１９－２４．

［１０］ 許諾． 基于改進ＰＳＯ 算法的ＵＡＶ 三維路徑規劃研究［Ｊ］． 電子測量技術，２０２２，４５（２）：７８－８３．

［１１］ 陳明強，李奇峰，馮樹娟，等． 基于改進粒子群算法的無人機三維航跡規劃［Ｊ］． 無線電工程，２０２３，５３（２）：３９４－４００．

［１２］ 許樂，趙文龍． 基于新型灰狼優化算法的無人機航跡規劃［Ｊ］． 電子測量技術，２０２２，４５（５）：５５－６１．

［１３］ 趙棣宇，鄭賓，殷云華，等． 改進粒子群算法的ＵＡＶ 突防路徑規劃［Ｊ］． 電光與控制，２０２３，３０（４）：１２－１６．

［１４］ ＸＵＥ Ｊ Ｋ，ＳＨＥＮ Ｂ． Ｄｕｎｇ Ｂｅｅｔｌｅ Ｏｐｔｉｍｉｚｅｒ：Ａ Ｎｅｗ Ｍｅｔａ-ｈｅｕｒｉｓｔｉｃ Ａｌｇｏｒｉｔｈｍ ｆｏｒ Ｇｌｏｂａｌ Ｏｐｔｉｍｉｚａｔｉｏｎ［Ｊ］Ｓｕｐｅｒｃｏｍ-ｐｕｔ，２０２３，７９：７３０５－７３３６．

［１５］ 宋立業，胡朋舉． 改進ＳＳＡ 在三維路徑規劃中的應用［Ｊ］． 傳感器與微系統，２０２２，４１（３）：１５８－１６０．

［１６］ 馮增喜，何鑫，崔巍，等． 混合隨機反向學習和高斯變異的混沌松鼠搜索算法［Ｊ］． 計算機集成制造系統，２０２３，２９（２）：６０４－６１５．

［１７］ 舒聰． 面向無人機航跡規劃的改進麻雀搜索算法及應用［Ｄ］． 廣州：廣州大學，２０２２．

［１８］ 歐陽城添，唐風，朱東林． 融合禁忌搜索的ＳＳＡ 算法及其路徑規劃的應用［Ｊ］． 電子測量技術，２０２２，４５（２２）：３２－４０．

作者簡介

遠翔宇 男，（１９９９—），碩士研究生。主要研究方向：路徑規劃、目標分配。

楊風暴 男，（１９６８—），博士，教授。主要研究方向：信息融合、不確定信息推理。

楊童瑤 女，（１９９７—），博士研究生。主要研究方向：威脅評估、意圖估計與態勢預測。