帶電粒子在有界磁場中運動的臨界問題研究

【摘要】通過對帶電粒子在磁場中的受力情況和軌跡變化進行深入探討，可以揭示其在不同條件下的臨界運動狀態.在高考中，這一課題也是考生們需要重點關注和掌握的內容之一，通過深入探究可以幫助他們更好地理解物理學的基本原理和應用.本文對帶電粒子在有界磁場中運動的臨界問題進行研究，歸納總結其解題方法，并舉例進行詳細分析講解，以期幫助學生對這一知識點有更深的理解，提高解題能力.

【關鍵詞】有界磁場；帶電粒子；臨界問題

1 帶電粒子在磁場中運動的臨界問題

帶電粒子在磁場中運動臨界問題的解答，通常可以從題目中的關鍵詞中找突破口.大多數臨界問題，其題干中常會出現“至少”“最大”“恰好”“不脫離”“不相撞”等特定的字詞以表明可能會涉及的臨界狀態，解題時一定要抓住這些線索，然后根據電磁學以及運動學知識，找出臨界條件，并根據臨界條件對問題進行分析解答.解答策略如下：

（1）兩種思路

①=1＼*GB3＼*MERGEFORMAT先一般再特殊，先求出問題的一般解（一般規律），然后針對性分析處于臨界條件時的特殊解（特殊規律）；

②=2＼*GB3＼*MERGEFORMAT直接分析、討論臨界狀態，找出臨界條件，從而通過臨界條件求出臨界值.

（2）兩種方法

物理方法：①=1＼*GB3＼*MERGEFORMAT利用臨界條件求極值；②=2＼*GB3＼*MERGEFORMAT利用邊界條件求極值；③=3＼*GB3＼*MERGEFORMAT利用矢量圖求極值.

數學方法：①=1＼*GB3＼*MERGEFORMAT用三角函數求極值；②=2＼*GB3＼*MERGEFORMAT用二次方程的判別式求極值；③=3＼*GB3＼*MERGEFORMAT用不等式的性質求極值；④=4＼*GB3＼*MERGEFORMAT圖象法.

2 帶電粒子在磁場中運動的三種模型分析

2.1 動態放縮法

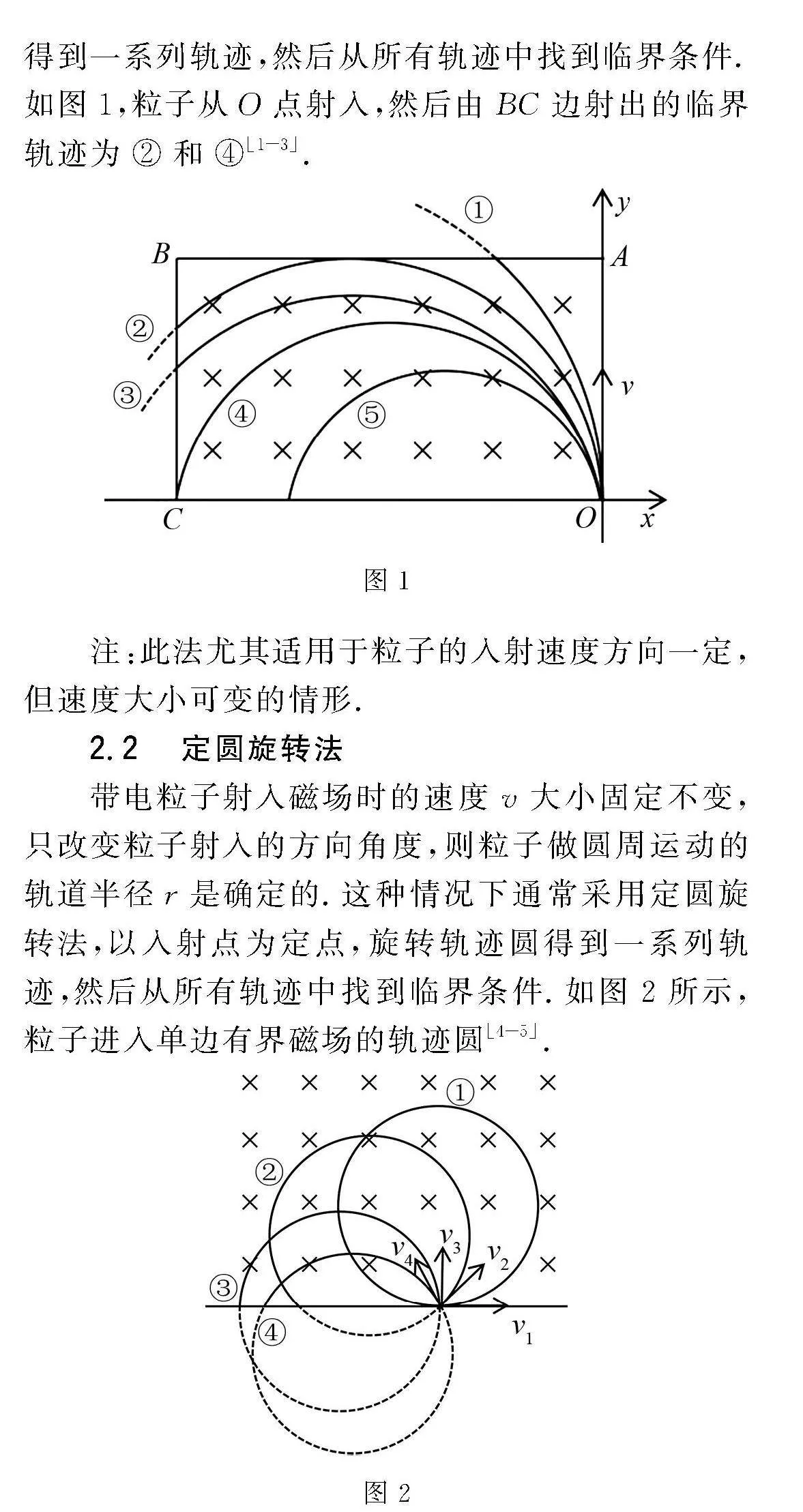
帶電粒子射入磁場的方向不變，但入射時的速度v或磁場的強弱B大小改變，粒子在磁場內做圓周運動的軌道半徑r也會隨之變化.這種情況下通常采用動態放縮法進行解答，對軌道半徑進行放縮，得到一系列軌跡，然后從所有軌跡中找到臨界條件.如圖1，粒子從O點射入，然后由BC邊射出的臨界軌跡為②和④=4＼*GB3＼*MERGEFORMAT［1-3］.

圖1

注：此法尤其適用于粒子的入射速度方向一定，但速度大小可變的情形.

2.2 定圓旋轉法

帶電粒子射入磁場時的速度v大小固定不變，只改變粒子射入的方向角度，則粒子做圓周運動的軌道半徑r是確定的.這種情況下通常采用定圓旋轉法，以入射點為定點，旋轉軌跡圓得到一系列軌跡，然后從所有軌跡中找到臨界條件.如圖2所示，粒子進入單邊有界磁場的軌跡圓［4-5］.

圖2

注：此法尤其適用于粒子的速度大小不變，而速度方向可變的情形.

2.3 定圓平移法

當速度大小和方向相同的一排相同粒子進入直線邊界，可以采用定圓平移法.各粒子的軌跡圓弧可以由其他粒子的軌跡圓弧沿著邊界平移得到，如圖3所示.

圖3

3 例題詳解

例 如圖4所示，矩形邊界ABCD內存在磁感應強度為B的勻強磁場，方向垂直于紙面向里，AB長為2L，AD長為L.從AD的中點E以不同速率發射粒子，速度方向與AD成30°角，粒子帶正電，電荷量為q，質量為m，不計粒子重力與粒子間的相互作用，下列判斷正確的是（ ）

（A）粒子可能從BC邊離開.

（B）經過AB邊的粒子最小速度為3qBL4m.

（C）經過AB邊的粒子最大速度為qBLm.

（D）AB邊上有粒子經過的區域長度為2L.

圖4

解 因為粒子帶正電，則粒子運動的軌跡如圖5所示，當粒子的軌跡恰好與CD邊相切時，根據幾何關系得R1（1－cos60°）=L2，可得此時粒子軌跡半徑R1=L，粒子將從AB邊上離A點的距離為AM=R1（1+cos30°）=1+32L的M點離開磁場區域，故粒子不可能從BC邊離開，故（A）項錯誤.

根據洛倫茲力提供向心力qvB=mv2R，可得R=mvqB，可知當粒子軌跡半徑為R1=L時，即粒子軌跡與CD邊相切時，此時粒子從AB邊射出的速度最大，vmax=qBLm，故（C）項正確.

設當粒子恰好從AB邊的N點射出時，粒子速度為v1，軌跡半徑為R2，根據幾何關系得R2（1+cos60°）=L2，可得粒子軌跡半徑R2=L3，此時粒子從AB邊射出的速度最小，vmin=qBL3m.根據幾何關系，射出點N離A點的距離AN=R2cos30°=36L，故AB邊上有粒子經過的區域長度為MN=AM－AN=33+1L，故（B）（D）兩項錯誤.

圖5

4 結語

高考中關于帶電粒子在磁場中運動的臨界問題一直備受關注.在物理學中，帶電粒子在磁場中的運動是一個復雜而重要的現象，涉及磁場力和洛倫茲力等力的相互作用.在考試中，學生需要理解帶電粒子在磁場中受力的方向和大小，以及如何計算其軌跡和速度.這是一個需要深入理解和掌握的知識點，對于解題和應用都具有重要意義.希望考生能夠通過深入學習和實踐，充分掌握這一關鍵問題，取得優異的成績.

參考文獻：

［1］史洪星.帶電粒子在有界勻強磁場中運動的臨界和極值問題——兼談“動態圓”模型的教學研究［J］.中學物理教學參考，2023，52（30）：48-51.

［2］馬順存.帶電粒子在有界磁場中運動的臨界問題解析——以2020年高考全國卷Ⅰ物理第18題為例［J］.物理通報，2021（03）：131-132+138.

［3］胡衛雄，余任遠.情境為載體方法作引領問題為導向——以帶電粒子在有界磁場中臨界與極值的數理分析為例［J］.教學考試，2021（04）：23-26.

［4］初樂香，楊艷.帶電粒子在有界勻強磁場中運動的臨界問題探討［J］.中學物理教學參考，2022，51（18）：54-57.

［5］胡衛雄.從幾道高考題談有界磁場的臨界與極值問題的數理方法［J］.數理化解題研究，2021（01）：88-90.