微積分建模與Origin軟件模擬在中學物理試題命制中的研究

摘" 要：本文通過微積分建模和Origin軟件模擬對中學物理試題情境的合理性進行了研究，包括判斷題干信息是否恰當以及探討理想化處理的前提條件。將以微積分建模與Origin軟件模擬為代表的數學物理方法運用在試題命制中，能夠提升試題的科學性、答案的引導性與情境的合理性。

關鍵詞：微積分；模型建立；Origin；計算機模擬；數學物理方法

基金項目：本文系南京市教育科學“十四五”規劃項目“AI技術用于初中物理實驗教學的實踐研究”（課題編號：L/2022/018）的階段性研究成果。

物理學習是一個由淺入深、由特殊到一般的攀登過程。由于中學生的知識儲備、理解能力、邏輯思維仍處在成長階段，教師在試題命制時就需要以學生的認知水平為依據。［1］在實際過程中，參數的不當設置會導致物理意義丟失，理想情境下得到的答案可能會和生活實際存在一定偏差……這些問題都會潛移默化地誤導學生的認知。［2］為解決該問題，教師應掌握相應的數學物理方法以還原真實情境。在本文中，筆者以未浸沒球體浮力的計算、空氣阻力對運動的影響兩個問題為例，運用微積分建模并輔以Origin軟件模擬展開討論。

1" 對一道浮力圖像題的分析與思考

1.1" 原題情境呈現

如圖甲所示，水平面上有個質量為2.5 kg、底面積為0.25 m2的正方體水槽，水槽內有一個實心球。逐漸往水槽內加水，球對水槽底部的壓力F與水深h的關系如圖乙所示，水深h＝7 cm時，球剛好有一半體積浸入水中（不考慮水槽厚度，水的密度ρ水＝1.0×103 kg/m3，g取10 N/kg）。

1.2" 題目分析

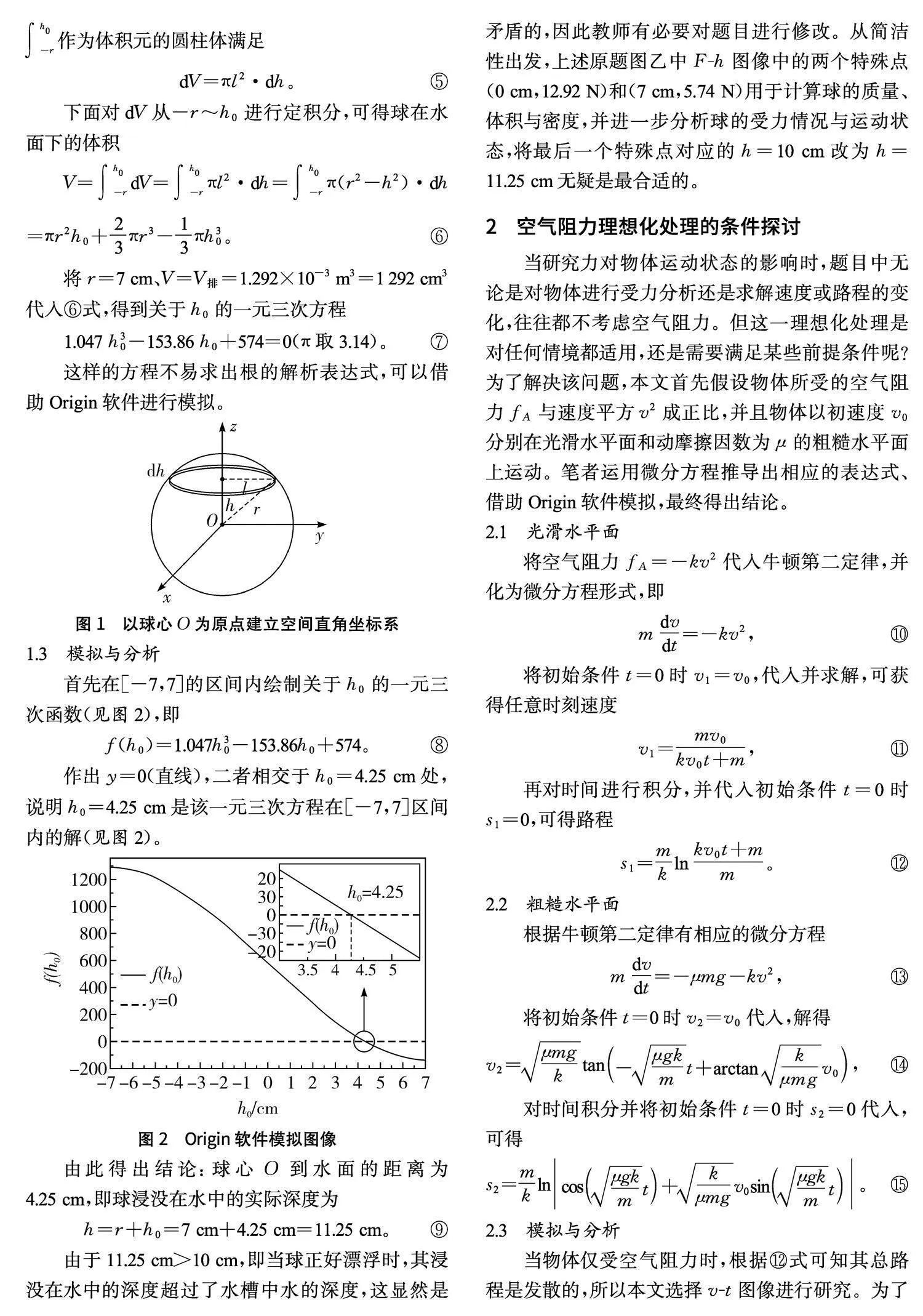
當水槽中水的深度h＝0cm時，球對水槽底部的壓力恰好等于球的重力，有F|h＝0＝G＝12.92 N，即球的質量m球＝1.292 kg。

根據題意，當水深h1＝7 cm時，球有一半體積浸入水中。由于球對水槽仍有壓力，說明此時球與容器底部直接接觸。由題可知球的半徑r＝7 cm，體積與密度分別為

V球＝43πr3≈1.437×10－3 m3；①

ρ球＝m球V球＝1.292 kg1.437×10－3 m3≈0.9×103 kg/m3。②

由ρ球＜ρ水可知，球最終會處于漂浮狀態。末狀態確定后，根據二力平衡F浮＝G，將數據代入，解得漂浮時排開水的體積為

V排＝1.292×10－3 m3。③

V排是實心球在水下的體積，它對應的深度h2又是多少？從圖乙可知，h2＝10 cm，但這是問題的真相嗎？筆者嘗試用微積分計算此時球浸沒在水中的實際深度。

以球心O為原點建立空間直角坐標系，在距球心h處作一半徑為l、厚度為dh的圓柱體（見圖1），其幾何關系滿足

h2＋l2＝r2（－r≤

h≤h0），④

其中r為球的半徑，h0為球心O到水面的距離。

∫h0－r

作為體積元的圓柱體滿足

dV＝πl2·dh。⑤

下面對dV從－r～h0進行定積分，可得球在水面下的體積

V＝∫h0－rdV＝∫h0－rπl2·dh＝∫h0－rπ（r2－h2）·dh＝πr2h0＋23πr3－13πh30。⑥

將r＝7 cm、V＝V排＝1.292×10－3 m3＝1292 cm3代入⑥式，得到關于h0的一元三次方程

1.047 h30－153.86 h0＋574＝0（π取3.14）。⑦

這樣的方程不易求出根的解析表達式，可以借助Origin軟件進行模擬。

1.3" 模擬與分析

首先在［－7，7］的區間內繪制關于h0的一元三次函數（見圖2），即

f（h0）＝1.047h30－153.86h0＋574。⑧

作出y＝0（直線），二者相交于h0＝4.25 cm處，說明h0＝4.25 cm是該一元三次方程在［－7，7］區間內的解（見圖2）。

由此得出結論：球心O到水面的距離為4.25 cm，即球浸沒在水中的實際深度為

h＝r＋h0＝7 cm＋4.25 cm＝11.25 cm。⑨

由于11.25 cm＞10 cm，即當球正好漂浮時，其浸沒在水中的深度超過了水槽中水的深度，這顯然是矛盾的，因此教師有必要對題目進行修改。從簡潔性出發，上述原題圖乙中F-h圖像中的兩個特殊點（0 cm，12.92 N）和（7 cm，5.74 N）用于計算球的質量、體積與密度，并進一步分析球的受力情況與運動狀態，將最后一個特殊點對應的h＝10 cm改為h＝11.25 cm無疑是最合適的。

2" 空氣阻力理想化處理的條件探討

當研究力對物體運動狀態的影響時，題目中無論是對物體進行受力分析還是求解速度或路程的變化，往往都不考慮空氣阻力。但這一理想化處理是對任何情境都適用，還是需要滿足某些前提條件呢？為了解決該問題，本文首先假設物體所受的空氣阻力fA與速度平方v2成正比，并且物體以初速度v0分別在光滑水平面和動摩擦因數為μ的粗糙水平面上運動。筆者運用微分方程推導出相應的表達式、借助Origin軟件模擬，最終得出結論。

2.1" 光滑水平面

將空氣阻力fA＝－kv2代入牛頓第二定律，并化為微分方程形式，即

mdvdt＝－kv2，B10

將初始條件t＝0時v1＝v0，代入并求解，可獲得任意時刻速度

v1＝mv0kv0t＋m，B11

再對時間進行積分，并代入初始條件t＝0時s1＝0，可得路程

s1＝mklnkv0t＋mm。B12

2.2" 粗糙水平面

根據牛頓第二定律有相應的微分方程

mdvdt＝－μmg－kv2，B13

將初始條件t＝0時v2＝v0代入，解得

v2＝μmgktan－μgkmt＋arctankμmgv0，B14

對時間積分并將初始條件t＝0時s2＝0代入，可得

s2＝mklncosμgkmt＋kμmgv0sinμgkmt。B15

2.3" 模擬與分析

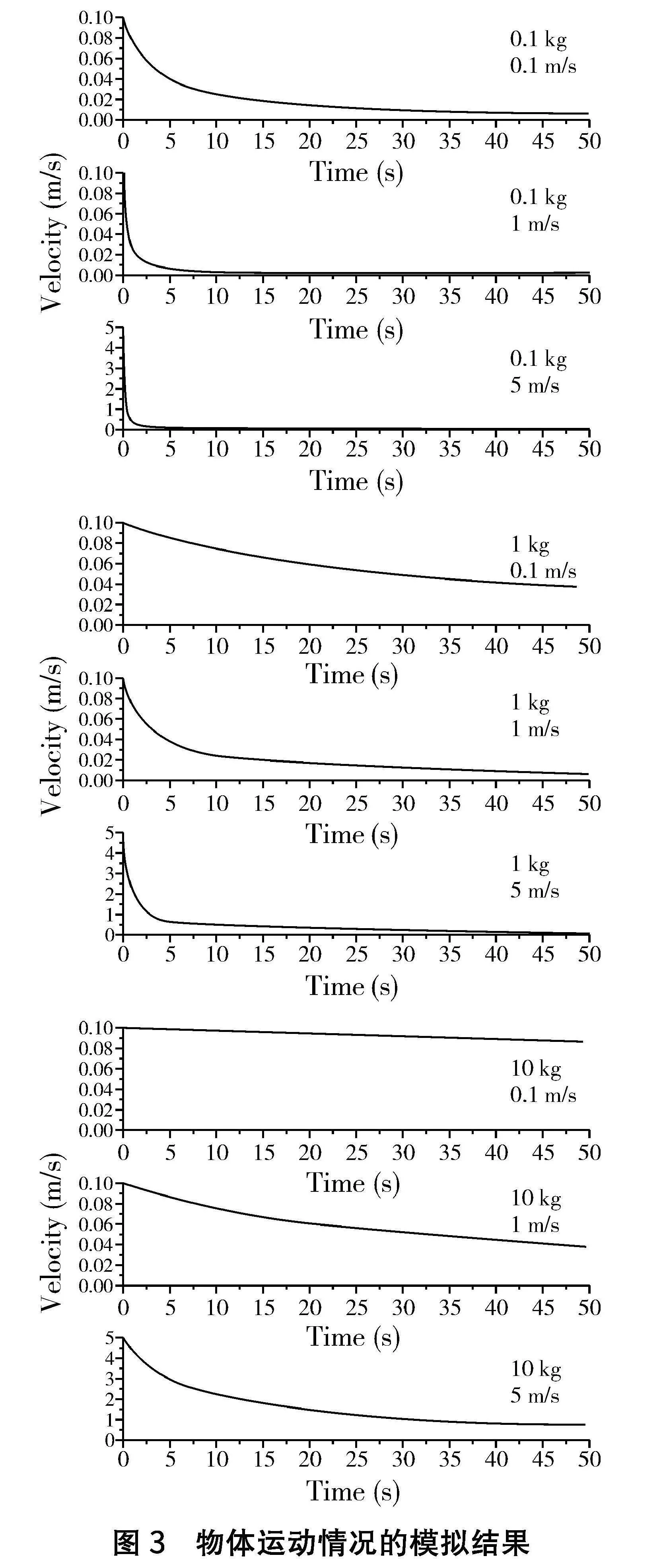
當物體僅受空氣阻力時，根據B12式可知其總路程是發散的，所以本文選擇v-t圖像進行研究。為了讓結果更具有實際意義，筆者分別模擬了空氣阻力系數k＝0.3的條件下，質量為0.1 kg、1 kg、10 kg且初速度分別為0.1 m/s、1 m/s、5 m/s的物體的運動情況，根據模擬結果（見圖3），可以得出如下結論：①對于質量相同的物體，初速度越大，速度的衰減越明顯；②對于初速度相同的物體，質量越小，速度的衰減也越明顯。

模擬的物理意義在于，無論是實驗室教學還是試題編寫，如果想將某一段運動近似看作勻速直線運動，可以讓質量較大的物體以較小的初速度運動，這樣可以使得在較短的時間內的結果更理想化；或者讓質量大的物體以較大的初速度運動，一段時間后也可近似為勻速直線運動。

當物體同時受摩擦力與空氣阻力時，可以直接研究其運動路程與初速度的關系。筆者依然選擇質量為0.1 kg、1 kg和10 kg的物體作為研究對象，動摩擦因數μ＝0.3，空氣阻力系數k＝0.3，重力加速度g取10 m/s2。本文分別模擬了不考慮空氣阻力和考慮空氣阻力時

運動路程s與初速度

v0的關系（見圖4）。

由圖可知：①當初速度小于2 m/s時，多條曲線重合度較高，說明此時物體的運動可近似視作只受摩擦力作用的勻變速直線運動；②當初速度大于5 m/s時，不考慮空氣阻力的曲線與其他三條曲線間出現明顯的差值，且物體質量越小、差值越大，說明此時空氣阻力對物體運動的影響不可忽略，且對質量較小物體的影響更明顯。［3］

模擬的物理意義在于，無論是“探究阻力對物體運動的影響”，還是對勻變速直線運動的研究，由于研究對象的質量不會很大，這就要求初速度一定要小，這樣才可以有效減小空氣阻力的影響，進而觀察到較為理想的現象。

3" 結語

研究物理問題時，教師除了要關注題目內部核心考點的滲透性與參考答案的引導性以外，還要關注題目本身情境設置的物理性與科學性。這就需要教師掌握以科學建模和軟件模擬為代表的一類數學物理方法，并將其運用到實際中，使試題變得更加嚴謹，從而在潛移默化中培養學生嚴謹務實的科學思維。

參考文獻

［1］胡道成.問渠那得清如許" 為有源頭活水來——談編寫物理原創試題的一些取材途徑及關鍵問題［J］.教學考試，2018（13）：71-74．

［2］任少鐸.2021年中考物理試題中的幾種典型錯誤分析［J］.物理通報，2022（11）：137-139，161．

［3］王振鑫，蘇文斌，時彥朋.探究空氣阻力對球體斜拋運動的影響［J］.科技風，2023（8）：163-165．