求解火箭噴氣極限速度的方法進階


摘 要:火箭噴出氣體后獲得的速度存在上限,該極限速度的求解過程涉及的思維方法較為復雜,學生可能難以一次性理解。因此,教師教學時需要采用小步子、多臺階的教學策略,引導學生逐步克服思維方法的難點。
關鍵詞:噴氣;極限速度;進階
1 引言
火箭噴氣問題屬于動量守恒應用中的反沖模型,由于它涉及相對速度、微元法、數列求和等知識和方法,因此學生只有處于關聯結構水平或拓展抽象水平,才能解決該問題。[1]此外,每個知識或方法單獨來看都構成難點,因此,在解決這類問題時,應采取小步子、多臺階的教學策略,逐步引導學生分步解決問題,確保每一步所涉及的知識與方法都落在學生的最近發(fā)展區(qū)內。
2 方法進階
2.1 第一臺階:氣體相對火箭以速度u一次噴出假定氣體相對火箭以速度u一次性全部噴出,噴出氣體的質量為m,火箭噴氣前的總質量(包括燃料質量)為M,噴氣前的速度為v0,求噴氣后火箭的速度v
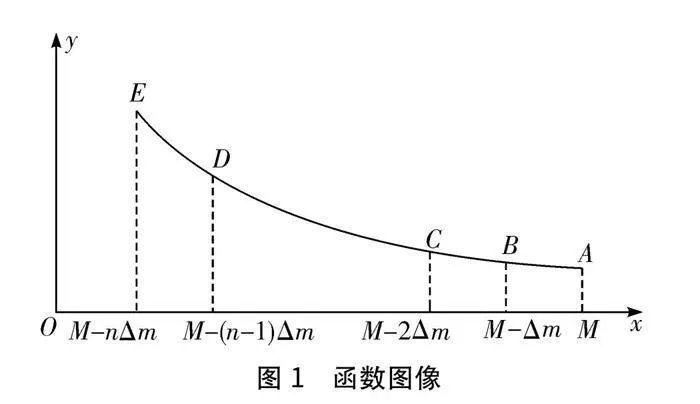
第三臺階相比第二臺階,不僅在解題思路上實現了質的飛躍,而且整個解題過程將應用數學知識解決物理問題的精髓展現得淋漓盡致。首先,采用微元法將氣體分成n等份,以體現微積分的核心思想;其次,運用方程的思想,列出了n個動量守恒的方程;再次,通過數列累加求和的方法,巧妙地消去了v1、v2等中間變量;最后,利用定積分完成了求和,完美收尾。這一過程充分展示了數學與物理的深度融合。
3 反思提升
3.1 教學中應分散難點
一個題目的最終問題可能包含多個難點,因此,教師需要設計一系列小步驟和多級臺階式的小問題,確保每個小問題的解決都落在學生的最近發(fā)展區(qū)內,使學生能夠通過自身努力逐步達到最終目標。在實際題目設計中,問題應以難度逐漸增加的序列呈現。無論是平時的練習題還是選拔性考試題,都應體現這種漸進性的設計原則,即前面的問題為后面的問題打下基礎,或者選項A、B、C為選項D做鋪墊,以此確保一道題目能夠均衡地覆蓋不同難度層次,進而全面考查學生的知識掌握情況和解題能力。
3.2 教學中應注重數理結合
數學是物理學習中不可或缺的工具,尤其是方程和函數的應用,在物理中發(fā)揮著不可替代的作用。物理概念構成了物理學習和思考的基礎單元;物理規(guī)律揭示了物質在運動變化過程中各個因素之間的本質聯系,展現了客觀事物本質屬性之間的內在聯系和必然性。物理學是以基本概念和基本規(guī)律為主干的完整體系,其中物理基本規(guī)律是這一體系的核心。[2]物理基本規(guī)律往往是定量的,如力學中的牛頓第二定律、牛頓第三定律及萬有引力定律,電磁學中的庫侖定律、法拉第電磁感應定律,以及熱學中的氣體狀態(tài)方程等,都是以方程的形式呈現。解決物理問題的過程通常是一個融合邏輯演繹和歸納綜合的復雜過程,伴隨著多個公式的聯立與推導。
3.3 教學中應以情境問題串啟發(fā)學生
《普通高中物理課程標準(2017年版2020年修訂)》在教學建議中明確指出教學設計和教學實施過程中重視情境的創(chuàng)設,通過問題解決促進學科核心素養(yǎng)的達成。[3]情境化的問題串的設計不僅提供了生動的情境,還設置了一系列深度和難度逐漸增加的問題。在解決問題的過程中,學生需要運用基本概念、基本規(guī)律以及相應的方法和策略。這一過程涉及物理觀念、科學思維、科學探究,并且在特定的情境中還包括科學態(tài)度和責任。
在上述案例中如果給字母賦予數值,令M=3m,速度極限增量為uln1.5,約為0.405u;令M=2m,速度極限增量為uln2,約為0.693u;令M=1.5m,速度極限增量為uln3,約為1.099u。可見增加燃料質量占飛船總質量比重的意義重大,而制約這一占比的關鍵因素就是材料強度。教師借此在學生心中埋下研究出強度大、密度小的材料的種子,引導學生樹立服務國家重大戰(zhàn)略的遠大理想。
參考文獻
[1]John B.Biggs, Kevin F. Collis. Evaluating the quality of learning:The SOLO taxonomy[M].New York:Academic Press,1982:24-25.
[2]喬際平,邢紅軍.物理教育心理學[M].南寧:廣西教育出版社,2002:63-75.
[3]廖伯琴.普通高中物理課程標準(2017年版2020年修訂)解讀[M].北京:高等教育出版社,2020:140.

