基于SARIMA-VMD-LSSVM的水產養殖溶解氧質量濃度預測

收稿日期：2023-05-25

基金項目：四川省科技成果轉移轉化示范項目（2020ZHCG0076）；工業控制技術國家重點實驗室開放課題（ICT2022B45）

作者簡介：唐 毅（1997-），男，四川江油人，碩士，主要研究方向為機器學習、智能水產養殖。（Tel）13320889755；（E-mail）tangyi970516@163.com

通訊作者：徐 全，（E-mail）quanxnjd@sina.com

摘要： 為了充分利用溶解氧質量濃度的數據特征，進一步提高水產養殖中溶解氧質量濃度預測的準確性，提出“線性與非線性”與“分解-預測-集成”相結合的溶解氧質量濃度預測模型。該模型首先由季節性差分自回歸滑動平均（SARIMA）模型對溶解氧質量濃度隨著時間變化而組成的數據序列（簡稱溶解氧質量濃度的時間序列）進行線性擬合，使用變分模態分解（VMD）對殘差序列進行分解，然后將各殘差分量代入經改進的灰狼算法（IGWO）優化的最小二乘支持向量機模型（LSSVM）中，得到非線性分量的預測結果。最后集成線性與非線性預測結果，得到最終的溶解氧質量濃度預測值。結果表明，與SARIMA、LSSVM、VMD-LSSVM模型相比，基于SARIMA-VMD-LSSVM模型對溶解氧質量濃度進行預測的精度顯著提高，預測的均方根誤差（RMSE）為0.078 7，平均相對誤差（MAPE）為0.022 6，說明該組合模型可有效提取溶解氧質量濃度的時間序列的多尺度特征，從而更精準地進行溶解氧質量濃度的預測。

關鍵詞： 水產養殖；溶解氧；變分模態分解；組合預測方法；改進的灰狼算法

中圖分類號： TP391；S912 文獻標識碼： A 文章編號： 1000-4440（2024）08-1473-10

PredictiMNP/kEgoEFb0DjfORnWYag==on of dissolved oxygen mass concentration in aquaculture based on SARIMA-VMD-LSSVM

TANG Yi， XU Quan， DU Bin， WANG Lei， YUAN Ruihao， YUAN Yu

（School of Mechanical Engineering， Xihua University， Chengdu 610039， China）

Abstract： In order to make full use of the data characteristics of dissolved oxygen mass concentration and further improve the accuracy of dissolved oxygen mass concentration prediction in aquaculture， a dissolved oxygen mass concentration prediction model combining "linear and nonlinear" and "decomposition-prediction-integration" was proposed. Firstly， the seasonal auto regressive integrated moving average （SARIMA） model was used to linearly fit the dissolved oxygen mass concentration time series， and the residual sequence was decomposed using variational mode decomposition （VMD）. Then， each residual component was substituted into the least square support vector machine （LSSVM） model optimized by the improved gray wolf algorithm （IGWO） to obtain the prediction results of the nonlinear component. Finally， the linear and nonlinear prediction results were integrated to obtain the final dissolved oxygen mass concentration prediction value. Experimental results showed that compared with SARIMA， LSSVM， and VMD-LSSVM models， the prediction accuracy of SARIMA-VMD-LSSVM model was significantly improved. The root mean square error （RMSE） was 0.078 7， and the mean absolute percentage error （MAPE） was 0.022 6， indicating that the combined model could effectively extract the multi-scale features of the time series of dissolved oxygen mass concentration， and achieve more accurate prediction.

Key words： aquaculture；dissolved oxygen;variational mode decomposition;combinatorial forecasting methods;improved gray wolf algorithm

在水產養殖中，溶解氧含量是養殖戶關心的重要參數之一，其含量過高或不足，都會嚴重影響水生生物的生長與健康，直接決定著養殖對象的產量和品質。目前，調節溶解氧含量常用的方法有實時或定時調節，然而由于數據傳輸及增氧機的啟動與停止都存在滯后性，僅依據現有數據進行溶解氧含量的調節，不僅難以改善水質，還可能引起水質指標的波動，不利于水生生物的健康[1]。因此，溶解氧含量的預測，能夠幫助養殖戶及時調控水質、優化養殖管理，最大限度地發揮水生生物的生產潛力，提高生產效益。

目前，統計預測、機器學習預測及組合模型預測等方法是對溶解氧含量進行預測的主要方法。其中，差分自回歸滑動平均（ARIMA）模型是統計預測中最常使用的模型，如Park等[2]使用ARIMA模型對洛東江口水質進行預測。隨著機器學習技術的不斷發展，其在數據預測領域的應用也越來越廣泛，在對水質的預測中也取得了不錯的效果，例如，張夢迪等[3]用反向傳播（BP）神經網絡模型實現了對多水質參數的預測；龔懷瑾等[4]使用變尺度混沌搜索優化的最小二乘支持向量機（LSSVM）模型，實現了對溶解氧含量的預測。然而，單一模型難以全面有效地表征溶解氧質量濃度隨著時間變化而組成的數據序列（簡稱溶解氧質量濃度的時間序列）的特征。因此，針對溶解氧含量的非線性與非平穩特征，“分解-預測-集成”的組合預測模型被廣泛應用于水質預測中。劉晨等[5]為了降低溶解氧質量濃度時間序列的復雜性，使用集合經驗模態分解（EEMD），再結合SVM實現了最終的預測。白雯睿等[6]將變分模態分解方法（VMD）與CNN-LSTM模型相結合，提升了溶解氧含量的預測精度。然而，上述方法未考慮溶解氧含量的數據特征，且在模型的選擇上未考慮預測的時效性。

為了彌補上述單一模型與組合模型在水質預測中的不足，本研究提出1種基于季節性差分自回歸滑動平均（SARIMA）-VMD-LSSVM的短時溶解氧質量濃度組合預測模型。SARIMA模型能夠識別具有周期性與非平穩時間序列的線性規律，且結構簡單，使用少量數據便可進行預測。VMD分解算法可用于充分削弱序列的非線性特征，同時能起到降噪的作用。LSSVM模型的訓練速度快，適用于非線性回歸問題，且對少量數據建模具有一定的優勢。因此，本研究擬通過將3種算法進行串聯組合用于水產養殖中溶解氧質量濃度的預測，并引入改進的灰狼算法優化LSSVM模型，以期避免LSSVM參數選擇的盲目性，進一步提升預測精度。

1 基本理論與模型的構建

1.1 SARIMA模型

SARIMA模型是由Jenkins與Box提出的一種時間序列預測模型，由自回歸模型（AR）與移動平均模型（MA）逐步發展而來，這類模型融合了時間序列分析和回歸分析的優點，并在此基礎上進一步發展，適用于存在周期性與非平穩性的序列，其一般形式如下：

1.4.2 改進的灰狼優化算法 GWO作為一種元啟發式優化算法，可以用來優化LSSVM的懲罰參數γ、σ。然而，GWO算法與大多數智能算法一樣，存在后期收斂速度慢、易陷入局部最優解等問題。因此，本研究引入非線性收斂因子，并結合麻雀算法中的探索者以提升算法跳出局部最優的能力與收斂速度。

（1）非線性收斂因子。在GWO算法中，收斂因子a從2到0線性遞減，無法對全局與局部搜索能力進行平衡。非線性收斂因子呈拋物線狀遞減，有利于提升全局搜索能力，在迭代后期快速遞減，有利于提升局部搜索能力。

a=2-2sinttmaxsin1μ（18）

式中，μ為調節系數，μ=0.5。

（2）麻雀算法優化。本研究將麻雀算法中探索者的大范圍搜索能力引入灰狼算法[10]，用于進一步提升GWO算法的搜索范圍與收斂能力。具體步驟如下：

步驟1：根據比例系數（ζ），將狼群劃分為探索者狼群與跟隨者狼群。

ζ=PNN-PN（19）

式中，N為灰狼總數；PN表示位置較好的探索者灰狼數量。

步驟2：探索者灰狼位置更新。

X（t+1）=X（t）e-tζ·tmax（20）

式中，ζ為[0，1]范圍內的隨機值。

步驟3：其他灰狼仍按照原灰狼優化算法進行位置更新。

1.4.3 改進的灰狼算法（IGWO）優化LSSVM 采用IGWO優化LSSVM的懲罰參數（γ）和徑向基寬度（σ），并以LSSVM最小均方差函數（MSE）作為目標函數，其表達式見公式（21）。

minf（γ，σ）=1m∑mi=1（xi-x^i）2（21）

式（21）中，xi表示真實值；x^i表示預測值。

使用IGWO優化LSSVM模型的具體步驟如下：

步驟1：初始化參數。生成20只灰狼，每只灰狼對應1組LSSVM的γ、σ，設置其取值范圍為（0.01～1 000.00），設置最大迭代次數為100。

步驟2：尋找最佳獵物。從第1只灰狼開始，根據公式（21）計算適應度，并按照適應度高低劃分灰狼等級，適應度較佳的前3匹狼分別表示為α狼、β狼、δ狼，剩下的狼則全為ω狼。

步驟3：位置更新。根據公式（20）對探索者灰狼進行位置更新，根據公式（17）對其他灰狼進行位置更新。

步驟4：判斷是否達到最大迭代次數，若達到，則輸出最優參數組合。

1.5 SARIMA-VMD-LSSVM模型的構建

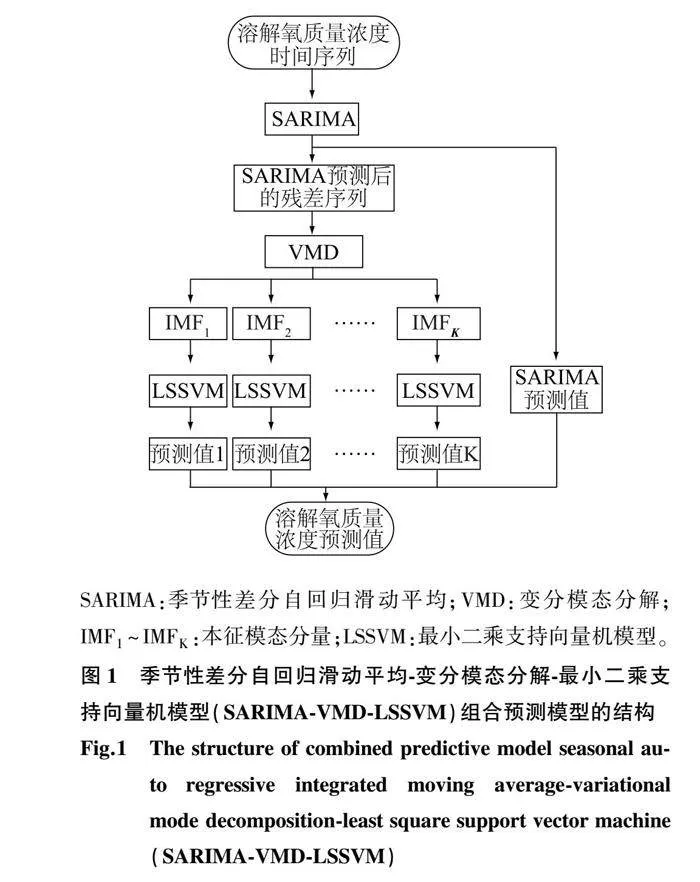
溶解氧質量濃度時序數據具有線性與非線性特征[11]，同時也存在周期性與非平穩性特征。由于單一模型無法適應所有特征結構的數據，因此擬合結果不佳。為了兼顧溶解氧質量濃度的所有數據特征，本研究提出基于SARIMA-VMD-LSSVM模型的水產養殖溶解氧質量濃度組合預測模型。其中，SARIMA模型能夠較好地體現時間序列的線性與周期性特征，且結構簡單；LSSVM模型訓練速度快，適用于非線性回歸問題。因此，本研究將SARIMA模型與LSSVM模型進行串聯結合，以充分發揮各模型的能力。然而，SARIMA模型擬合后的殘差序列匯聚了溶解氧質量濃度時間序列的非線性特征，且整體呈現出白噪聲特性，因此在進行LSSVM模型訓練之前，本研究引入VMD分解算法對殘差序列進行進一步的特征提取，以降低其非線性帶來的影響，增強可預測性。SARIMA-VMD-LSSVM組合模型的結構如圖1所示。

SARIMA-VMD-LSSVM模型的預測步驟具體如下：

步驟1：SARIMA建模及預測。根據SARIMA模型建模步驟，確定SARIMA模型參數，并對溶解氧質量濃度的時間序列（xt）進行擬合與預測，得到擬合序列{lt}與預測值（l^），借助公式（22）得到殘差序列{et}：

et=xt-lt（22）

步驟2：VMD分解。對{et}進行VMD分解，得到K個殘差分量{IMF1}、{IMF2}、… 、{IMFK}。

步驟3：LSSVM建模及預測。以{IMF1}、{IMF2}、… 、{IMFK}作為樣本集，對LSSVM進行訓練和預測，得到各殘差分量的預測值{IMF^1}、{IMF^2}、… 、{IMF^K}。

步驟4：結合SARIMA預測值和各殘差分量LSSVM預測值，得到最終預測值（Y^），即Y^=l^+IMF^1+IMF^2+…+IMF^K。

1.6 評價指標

對在本研究中模型的預測精度與誤差使用平均絕對百分比誤差（MAPE）、均方根誤差（RMSE）進行評估，其值越小，表明模型的性能越好。

MAPE=1m∑mi=1xi-x^ixi（23）

RMSE=1m∑mi=1（xi-x^i）2（24）

2 實例分析

2.1 數據來源

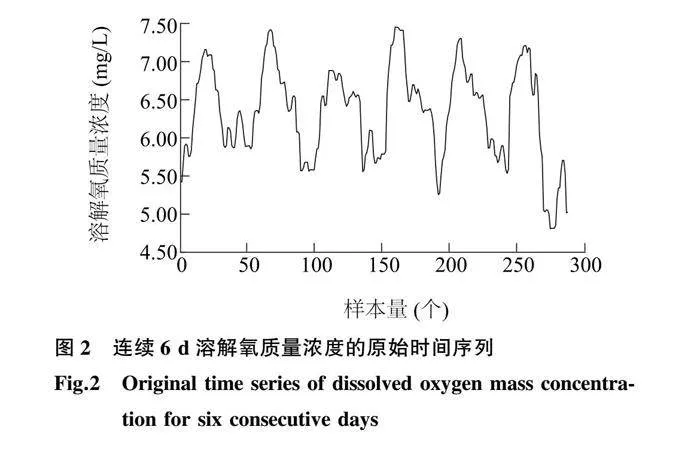
本研究采用的數據集來自文獻[12]中報道的海南省陵水黎族自治縣水產養殖基地收集的真實溶解氧質量濃度數據，并對溶解氧質量濃度數據集進行下采樣處理，每隔30 min采集1次，試驗數據共計2 985條。其中連續6 d的溶解氧質量濃度的時間序列如圖2所示。劃分訓練集與測試集的比例為8∶2，其中測試集用于進一步驗證經訓練集訓練后的溶解氧質量濃度預測模型的性能。

需要說明的是，本研究采用的預測方式是單步預測，即通過歷史時刻對下個時刻的預測值進行預測。由于樣本點過多，為了更好地展示溶解氧質量濃度序列的處理過程，下文中每個窗口僅展示其中連續的500個樣本點。同時，為了更好地對比最終預測結果與實測值之間的差異，預測結果的圖窗僅展示200個連續樣本點，但仍然使用全部測試集作為模型最終的評價標準。

仿真平臺具體參數：Window 10操作系統，4核1.80 GHz CPU，MatlabR 2022b。

2.2 SARIMA線性預測

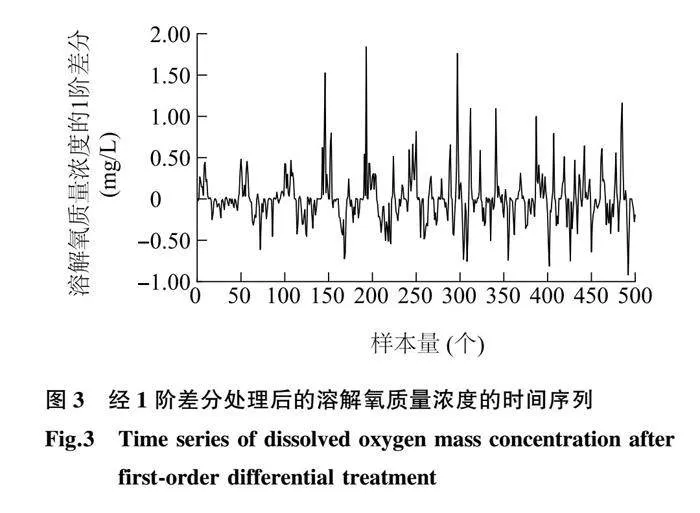
2.2.1 平穩化處理 首先通過MATLAB中的adftest函數對溶解氧質量濃度的時間序列進行單位根檢測（ADF），此時P=0.054 0（P>0.05），可知此時原溶解氧質量濃度的時間序列為非平穩序列。對溶解氧質量濃度的時間序列進行1階差分處理后，P=0.001 0（P<0.05），此時溶解氧質量濃度的時間序列整體表現平穩。如圖3所示，1階差分處理后的溶解氧質量濃度的時間序列仍存在周期性變化，因此還需對其進行1階季節性差分處理，結果如圖4所示。

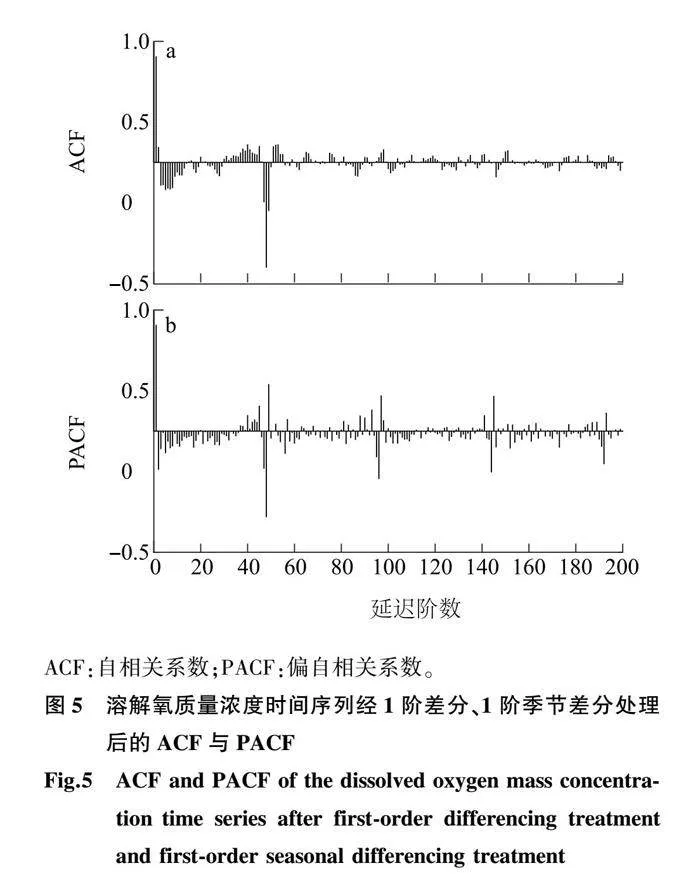
2.2.2 SARIMA模型參數定階 對溶解氧質量濃度時間序列進行1階差分與1階季節性差分處理，則d=0或1，D=0或1。溶解氧質量濃度采樣頻率為1次間隔0.5 h，則s=48。由圖5a可以看出，在延遲階數為1階、48階時溶解氧質量濃度的時間序列數據與歷史數據具有較強的相關性，即q=0或1，Q=0或1。由圖5b可以看出，在延遲階數為1階、2階時具有較強相關性，即p=0～2，在48階、96階、144階時溶解氧質量濃度的時間序列數據與歷史數據具有較強相關性，即P的取值范圍為0～3。

根據參數p、d、q、P、D、Q的初步定階結果，用SPSS中的正態貝葉斯信息量準則（BIC）確定最佳取值。正態BIC同時考慮模型擬合度與模型復雜度，其數值越小，表明模型越佳。最小正態BIC為-3.408，此時對應的最佳擬合度的模型為SARIMA（2，1，0）（1，1，1）48。

2.2.3 SARIMA對溶解氧質量濃度的預測 用SARIMA（2，1，0）（1，1，1）48對溶解氧質量濃度的時間序列進行預測，結果如圖6所示。同時得到預測后剩余的殘差序列，整體呈現白噪聲特征（圖7）。

2.3 VMD分解

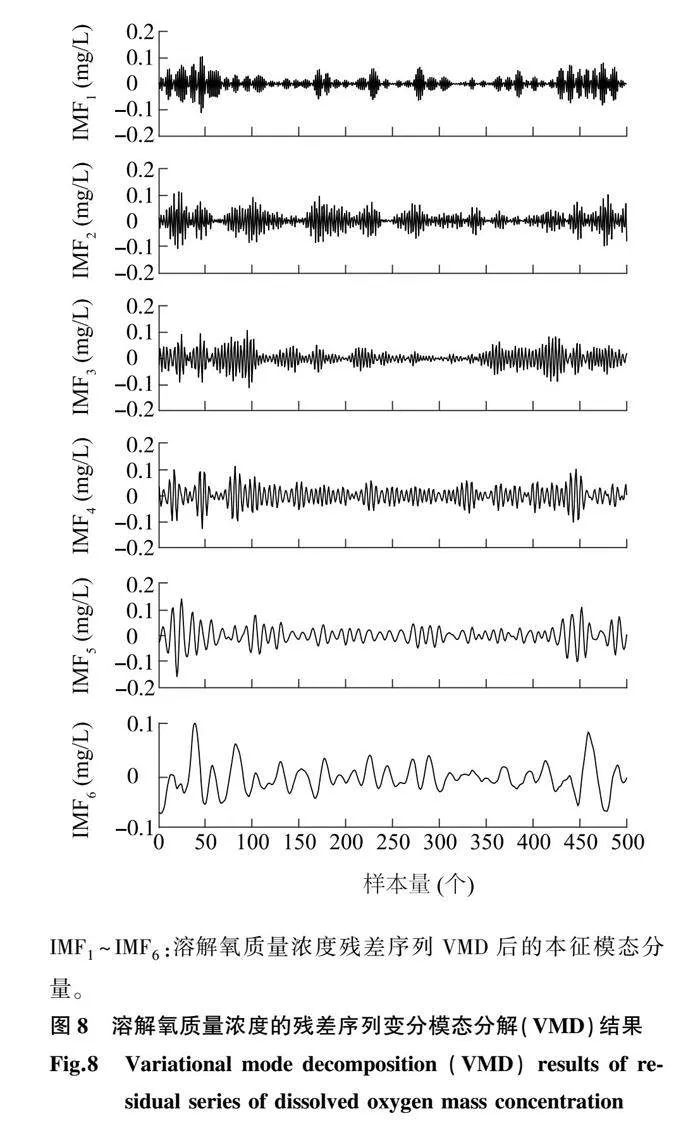
本研究依據最小峭度準則[13]，得到溶解氧質量濃度殘差序列的最佳分解層數為6。由圖8可以看出，各分量數據雖依舊保持較高頻率，但VMD分解依舊能夠分解出不同頻率的信號，且更具有規律性，由此提升了殘差數據的可預測性。

2.4 IGWO-LSSVM殘差預測

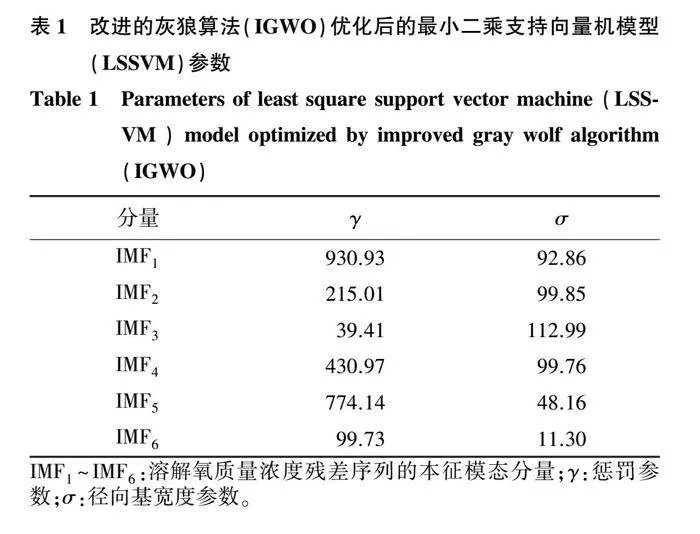
為了避免數據冗余帶來的影響，本研究用偏自相關系數（PACF）確定各分量的最佳嵌入維數。如圖9所示，前3個延遲（Lag）的偏自相關系數絕對值都大于0.6，說明IMF1時間序列在任意時刻的值都與其前3個歷史時刻的值密切相關，因此取最佳嵌入維數（m）=3。同理，得到IMF2～IMF6的最佳嵌入維數，分別為4、4、4、4、3。

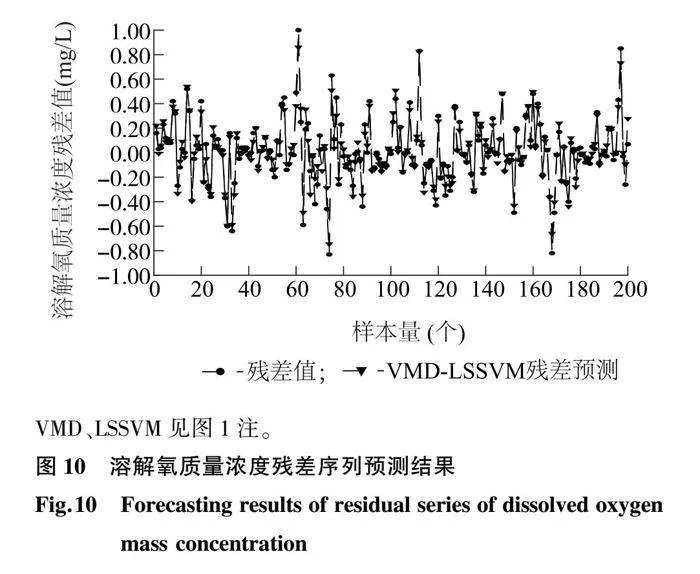
通過IGWO確定各殘差分量的最佳LSSVM模型參數，詳見表1。對各殘差分量進行LSSVM建模預測，并將各分量的預測結果疊加，得到最終殘差序列的預測結果，如圖10所示。

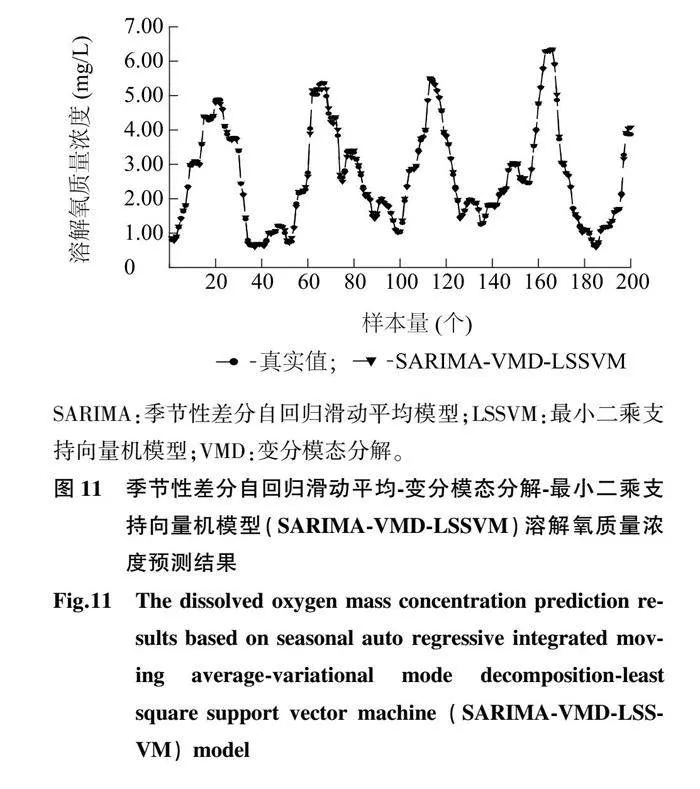
基于上述SARIMA模型，得到線性預測結果，其中通過LSSVM模型預測得到非線性結果，只需將2個分量進行集成，便可得到最終溶解氧質量濃度的預測值，結果見圖11。

2.5 模型對比分析

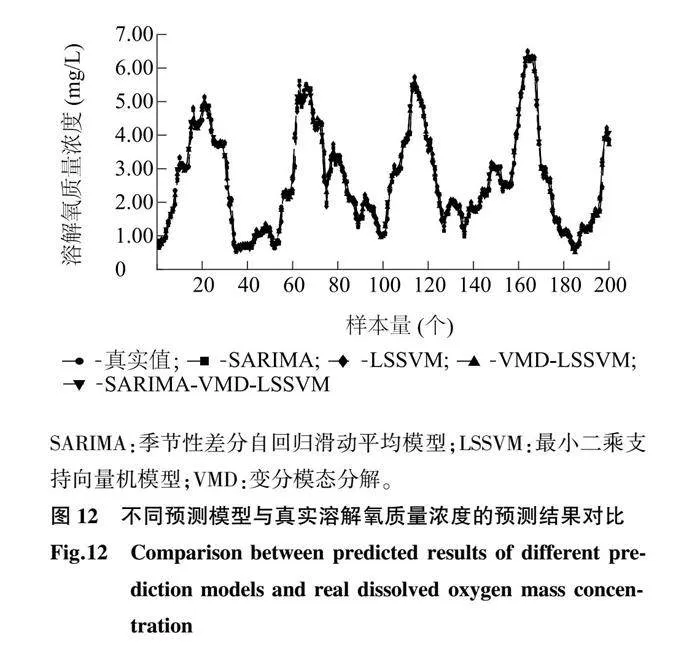
2.5.1 不同模型的對比分析 為了驗證本研究所提模型的預測性能，將SARIMA-VMD-LSSVM模型與單一模型SARIMA、LSSVM及組合模型VMD-LSSVM進行對比分析。如圖12所示，4種模型都能較好地預測溶解氧質量濃度的變化趨勢，但是也能明顯看出，SARIMA與LSSVM模型在轉折點的精度較差，這是由于單一模型難以學習到轉折點的信息。此外還可以看出，VMD-LSSVM與SARIMA-VMD-LSSVM的擬合程度較好。

進一步計算出4種模型的平均相對誤差（MAPE）、均方根誤差（RMSE）并記錄某一時刻所需的運行時間。如表2所示，與SARIMA、LSSVM模型相比，VMD-LSSVM、SARIMA-VMD-LSSVM組合模型的MAPE、RMSE明顯降低，其中SARIMA-VMD-LSSVM模型相較于VMD-LSSVM模型有更好的預測精度，說明本研究提出的模型能更加充分地挖掘溶解氧質量濃度的數據特征。由表2還可以看出，SARIMA-VMD-LSSVM組合模型整體預測時間僅有12.957 2 s，可見該組合模型適用于溶解氧質量濃度的短時間預測。

2.5.2 不同優化算法的對比 為了驗證改進灰狼算法的有效性，本研究選用粒子群優化算法（PSO）、蟻群優化算法（ALO）、灰狼優化算法（GWO）、改進灰狼優化算法（IGWO）分別對LSSVM懲罰參數和徑向基寬度參數進行尋優，并用優化后的LSSVM模型對SARIMA擬合后的溶解氧質量濃度殘差序列進行預測。由于殘差序列中存在值為0的情況，因此僅采用RMSE作為評價指標。在本研究中，設立種群數量為20個，最大迭代次數為100次。

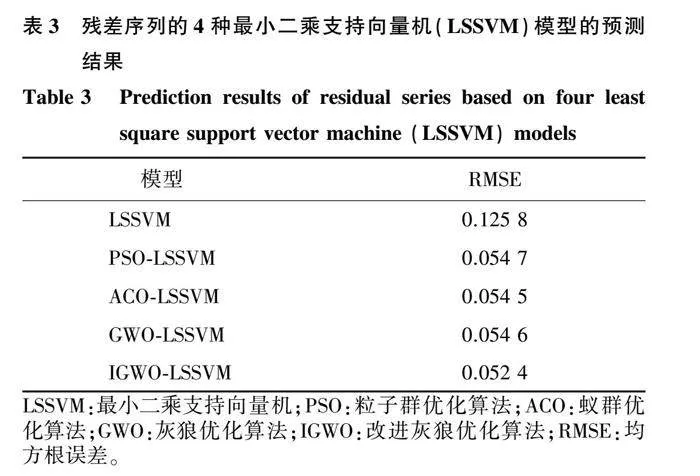
對用4種優化方法預測溶解氧質量濃度殘差序列的結果與真實殘差值（表3）進行比較發現，使用固定超參數的LSSVM模型的RMSE明顯較大，擬合程度不高，說明不同殘差分量所需的LSSVM模型各不相同。加入優化算法后，RMSE減小，整體預測效果提升。由于LSSVM超參數較少，僅為二維，因此優化后的LSSVM模型預測效果相近，但仍然能看出IGWO-LSSVM模型的RMSE低于其他模型，其原因是對于其他模型而言，某些殘差分量難以找到最優LSSVM模型，從而陷入局部最優。

為了進一步驗證IGWO的有效性，選取Sphere單峰函數、Ackely多峰函數和Griewank多峰函數進行測試[14]，并將測試結果與PSO、ALO、GWO算法所得結果進行比較，設各算法的種群規模為50個，最大迭代次數為100次。由表4可以看出，IGWO在不同測試函數中整體上有相對較好的尋優結果，其在不同維度下的Sphere函數的尋優精度較PSO、ALO和GWO算法高1～14個數量級。在不同維度下，Ackely函數IGWO算法的尋優精度比PSO、ALO和GWO算法高1～17個數量級。在Griewank函數中，IGWO算法在10～100維范圍均獲得理論最優值0；在300維，其理論最優值相較于PSO、ALO、GWO至少提升了7個數量級。由此可見，IGWO具有更好的全局搜索能力與收斂速度。

3 結論

為了充分利用溶解氧質量濃度的數據特征，進一步提升溶解氧質量濃度的預測精度，本研究將SARIMA模型、VMD模型與LSSVM模型相結合，同時引入改進的灰狼優化算法（IGWO），構建了用于預測水產養殖中溶解氧質量濃度的模型，得出以下結論：（1）通過改進GWO的收斂因子，并結合麻雀優化算法，有效提升了灰狼優化算法的尋優能力。避免了LSSVM參數設定的盲目性，減少了人工選擇參數的主觀影響。（2）將SARIMA模型、VMD模型與LSSVM模型3種模型結合，有效地表征了溶解氧質量濃度時間序列的周期性、線性、非線性與非平穩性特征。結果顯示，SARIMA-VMD-LSSVM模型的評價指標優于其單一模型與VMD-LSSVM模型，表明該組合模型更能有效挖掘溶解氧質量濃度的數據特征。（3）本研究中組合模型的主要預測原理為SARIMA、LSSVM，兩者都有較快的計算速度。試驗結果表明，組合模型總用時為12.957 2 s，適合用于溶解氧質量濃度的短時預測。本研究主要針對溶解氧質量濃度單因子進行研究，未來將嘗試將其與其他水質因子結合，以進一步提升預測精度。此外，還可以結合嵌入式、網絡通信和自動控制等技術，實現溶解氧質量濃度的在線預測與管控。

參考文獻：

[1] 謝雨茜， 李 路， 朱 明，等. 基于EMD與K-means的ILSTM模型在池塘溶解氧預測中的應用[J]. 華中農業大學學報（自然科學版），2022，41（3）：200-210.

[2] PARK K D， KANG D H， SO Y， et al. Water quality prediction using the ARIMA time series analysis model in the Nakdong River estuary[C]. San Francisco： AGU Fall Meeting Abstracts，2019.

[3] 張夢迪，徐 慶，劉振鴻，等. 基于動態滑動窗口BP神經網絡的水質時間序列預測[J]. 環境工程技術學報，2022，12（3）：809-815.

[4] 龔懷瑾，毛 力，楊 弘. 基于變尺度混沌QPSO-LSSVM的水質溶氧預測建模[J]. 計算機與應用化學， 2013，30（3）：315-318.

[5] 劉 晨，李 莎，叢孫麗，等. 基于EEMD和螢火蟲算法優化SVM的溶解氧預測[J]. 計算機仿真， 2021，38（1）：359-365.

[6] 白雯睿，楊毅強，郭 輝，等. 基于VMD-CNN-LSTM的珠江流域水質多步預測模型研究[J]. 四川輕化工大學學報（自然科學版），2022，35（4）：66-74.

[7] DRAGOMIRETSKIY K， ZOSSO D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing，2014，62（3）：531-544.

[8] LUO H， PAAL S G. Metaheuristic least squares support vector machine-based lateral strength modelling of reinforced concrete columns subjected to earthquake loads[J]. Structures，2021，33：748-758.

[9] MIRJALILI S， MIRJALILI S M， LEWIS A. Grey wolf optimizer[J]. Advances in Engineering Software，2014，69（3）：46-61.

[10]高 兵，鄭 雅，秦 靜， 等. 基于麻雀搜索算法和改進粒子群優化算法的網絡入侵檢測算法[J]. 計算機應用，2022，42（4）：1201-1206.

[11]胡衍坤，王 寧，劉 樞，等. 時間序列模型和LSTM模型在水質預測中的應用研究[J]. 小型微型計算機系統，2021，42（8）：1589-1573.

[12]LIU J T， YU C， HU Z H， et al. Accurate prediction scheme of water quality in smart mariculture with deep Bi-S-SRU learning network[J]. Ieee Access，2020，8（99）：24784-24798.

[13]鄭 圓，胡建中，賈民平，等. 一種基于參數優化變分模態分解的滾動軸承故障特征提取方法[J]. 振動與沖擊，2020，39（21）：195-202.

[14]崔東文，袁樹堂. 基于WPD-AHA-ELM模型的水質時間序列多步預測[J]. 三峽大學學報（自然科學版），2023，45（1）：6-13.

（責任編輯：徐 艷）