例析水平面內圓周運動的臨界問題

物體在水平面內的圓周運動的向心力可以是某一個力，也可以是幾個力的合力．當物體的角速度或者線速度變化時，會引起物體受力的變化，受力的變化也會導致角速度或者線速度發生變化．物理量變化過程一般會涉及臨界問題，該類問題考查的知識內容點多面廣，能力要求較高，學科素養導向明顯，備受命題者青睞．

１ 支持力臨界

如果繩連接物體在圓錐體表面做圓周運動的向心力是繩的拉力，當物體的運動狀態變化時，會引起圓錐體表面的支持力的變化，當支持為０時，往往物體的變化規律發生突變，抓住支持力為０時的物體的受力和運動特點，是解決問題的關鍵．

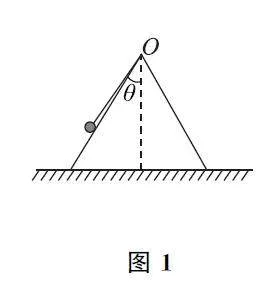
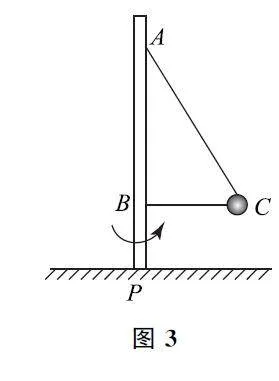
例１ 如圖１所示，一個光滑的圓錐體固定在水平桌面上，其軸線豎直，母線與軸線之間夾角為θ，一條長度為l 的輕繩，一端固定在圓錐體的頂點O 處，另一端拴著一個質量為m 的小球（可看作質點），小球以角速度ω 繞圓錐體的軸線做勻速圓周運動，細線拉力F 隨ω２ 變化關系如圖２ 所示．重力加速度g 取１０m·s－２，由圖２可知（ ）．

A．小球的角速度為２.５rad·s－１時，剛離開錐面

B．母線與軸線之間夾角θ＝３０°

C．小球質量為０.６kg

D．繩長為l＝２m

解析 根據圖２可知，當小球的角速度滿足ω２ ＝２５＇４rad２·s－２時，小球恰好要離開錐面，此時角速度為ω＝５／２rad·s－１，故選項A 正確．

當小球將要離開錐面時，繩子拉力與小球重力的合力提供向心力，有Fsinθ＝mω２lsinθ，即F＝mω２l．當小球離開錐面后，設繩子與豎直方向的夾角為α，繩子拉力與小球重力的合力提供向心力，有Fsinα＝mω２lsinα，即F＝mω２l，則根據圖２，結合所得繩子拉力F 與ω２ 的函數關系可知，當小球離開錐面后ml＝１kgm．當小球未離開錐面時，分析小球受力情況，水平方向根據牛頓第二定律有Fsinθ－FNcosθ＝mω２lsinθ，豎直方向根據平衡條件有Fcosθ＋FNsinθ＝mg，聯立可得F ＝mlsin２θω２＋mgcosθ，根據圖２，結合所得函數關系可得mlsin２θ＝ ９／２５kg·m，mgcosθ＝４N，聯立解得θ＝３７°，l＝２m，m ＝０.５kg．故選項D正確，選項B、C錯誤．

點評 細繩的拉力發生變化時，圓錐體對小球的彈力也發生變化，圓錐體與小球間彈力為０是此類問題的臨界狀態．

２ 細繩拉力臨界

當細繩的拉力提供圓周運動的向心力時，細繩的拉力往往隨物體的運動狀態的變化而變化，涉及兩條細繩時，哪條細繩先達到臨界狀態是分析的重點．

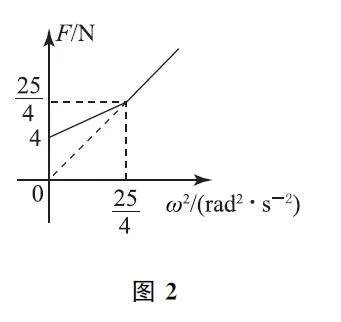
例２ 如圖３所示，AP 為豎直轉軸，P 端放在地面上，細繩AC 和BC 的結點C 系一質量為m 的小球，兩繩能承擔的最大拉力均為２.２５mg，當AC 和BC 均拉直時∠ABC ＝９０°，∠ACB ＝５３°，細繩AC 長度為L＝２ m，ABC 能繞豎直軸AP勻速轉動，因而小球在水平面內做勻速圓周運動，當小球的轉速增大時，兩繩均會被拉斷，g 取１０m·s－２，sin５３°＝0.８，cos５３°＝０.６．