晶體結構與性質考點歸類分析

晶體結構與性質的相關題目往往以新科技、新能源等社會關注的熱點問題為出發點,考查學生的抽象思維和邏輯推理能力,是高考的必考點之一.本文介紹了晶體結構與性質的常見題型,以提高學生對該部分內容的理解能力.
1 考查晶胞化學式
晶胞化學式的書寫,考查的是晶胞中微粒的個數,核心思想在于“均攤”.當用均攤法進行計算時,首先觀察晶胞的結構,確定微粒的位置,然后運用均攤法進行計算,得出某個微粒的個數,最后寫出正確的化學式.。
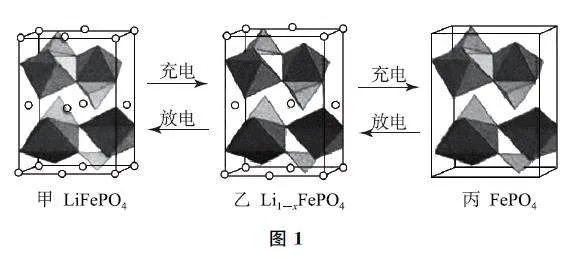
例1 LiFePO4 的晶胞結構示意圖如圖1G甲所示,其中O 圍繞Fe和P分別形成正八面體和正四面體,它們通過共頂點、共棱形成空間鏈結構,每個晶胞中含有LiFePO4 的單元數有____個.。
電池充電時,LiFePO4 脫出部分Li+ ,形成Li1-xFePO4,結構示意圖如圖1G乙所示,則x =____,n(Fe2+ )∶n(Fe3+ )=____.。
分析 本題將電化學知識和電極材料的晶體結構進行了結合,具有一定的創新性.學生解決該題的第一個思維障礙點在于如何理解LiFePO4 晶胞結構的示意圖.常規題型會對示意圖中的微粒進行說明,明確微粒的具體成分,但該題并未對該部分作出闡釋,僅僅給出了充放電過程中不同物質的晶胞結構示意圖,需要學生對示意圖中的微粒進行自主分析判斷,對學生的觀察理解能力有更高的要求.可以從兩個方面進行思考.一是通過觀察圖像發現,只有“小圓球”發生了變化,其余均保持不變,且物質由LiFePO4變化為Li1-xFePO4 再變化為FePO4,說明小圓球代表Li+ .二是根據題干信息“O 圍繞Fe和P分別形成正八面體和正四面體”容易推知小圓球代表Li+ .第二個思維障礙點在于計算晶胞中“含有LiFePO4 的單元數”.常見題型中,無論計算哪種微粒在晶胞中的個數,都能夠計算出單元數.但該題只能從“Li+ ”的微粒數進行分析,其他微粒的計算則相對較困難.根據圖1G甲可知,頂點上Li+ 數目為8×1/8=1,面上Li+ 數目為4×1/2=2,棱上Li+ 數目為4×1/4=1,1個晶胞中含有Li+ 的數目為1+2+1=4,故每個晶胞中含有LiFePO4 的單元數為4.據圖1G乙可知,頂點上Li+ 數目為8×1/8=1,面上Li+ 數目為3×1/2=1.5,棱上Li+ 數目為3×1/4=0.75,共有Li+ 數目為3.25,根據圖1G甲、圖1G乙中含有Li+ 數列等式有1/1-x = 4/3.25,計算可得x = 3/16.圖1G乙所代表物質的化學式為Li13Fe16(PO4)16,則根據化合物中正、負化合價的代數和為0可知,n(Fe2+ )∶n(Fe3+ )=13∶3.
2 考查晶體密度
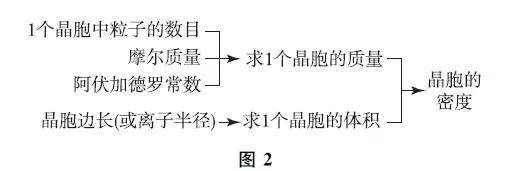
晶體密度是高考常見的考點之一.可以按照圖2所示步驟展開計算.
第1步:計算1mol晶胞的質量(均攤思想).
1mol晶胞的質量可以寫作XM ,其中X 為1個晶胞中包含化學式的個數;M 是化學式對應的摩爾質量.
第2步:計算1mol晶胞的體積.
第3步:根據公式ρ=m/V 算出晶體密度.
在進行晶體密度計算時,需要注意單位的換算.
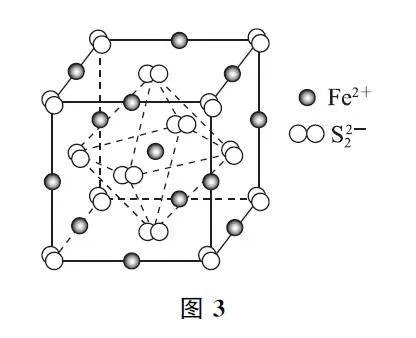
例2 FeS2 晶體的晶胞如圖3所示,晶胞邊長為a nm、FeS2 相對分子質量為M 、阿伏加德羅常數的值為N A,其晶體密度的計算表達式為____g·cm-3.
分析 第1步:計算1mol晶胞的質量.對晶胞的結構進行分析,可以發現頂點和面心位置被S22- 占據;棱邊和體心位置被Fe2+ 占據.則在該晶胞中,S22-的個數為6×1/2+8×1/8=4;Fe2+ 的個數為12×1/4+1=4,因此,1個晶胞中含有的FeS2 單元數為4;FeS2的摩爾質量是M ,故1mol晶胞(含4molFeS2)的質量為4M .
第2步:計算1mol晶胞的體積.由于是立方晶胞,且FeS2 晶胞的邊長為a nm,1個晶胞的體積為(a×10-7)3cm3,則1mol晶胞的體積為N A ×a3×0-21cm3.
第3步:根據公式計算晶體密度ρ=m/V = 4M/N Aa3×10-21 g·cm-3.
3 考查微粒分數坐標參數
在高中化學教學過程中,涉及書寫微粒分數坐標參數的試題可能不會頻繁出現在學生的課本和習題中,但近年高考試卷中經常出現該類題型.通常情況下,這類試題的出題方式是先給出一些相關的微粒(如離子、原子等)的分數坐標信息,接著要求學生利用微粒分數坐標參數對特定的其他微粒進行準確的位置描述.這樣的題目設計旨在考查兩個方面的能力:首先,考查學生是否能夠有效地從題目中提取關鍵信息,并且理解這些信息在三維空間坐標系中的具體含義,即是否具備建立三維坐標的能力;其次,考查學生是否能夠將化學知識與數學知識相結合,通過數學工具來解決化學領域中的具體問題,這反映了學生跨學科知識整合的能力.解答微粒分數坐標參數相關試題時,可以按照如下步驟進行:
第1步:根據已知微粒的坐標確定坐標系原點.
第2步:根據已知微粒坐標,確定坐標系的走向,建立三維坐標系,一般以坐標軸所在正方體的棱長為1個單位.
第3步:從微粒所在位置分別向x、y、z 軸作投影,所得坐標軸上的截距即為該原子的分數坐標.
例3 S與Zn所形成化合物晶體的晶胞如圖4所示.原子坐標參數可表示晶胞內部各原子的相對位置.如圖4晶胞中,原子坐標參數a 為(0,0,0);b 為(1/2,0,1/2);c 為(1/2,1/2,0),則d 的坐標參數為____.
分析 第1步:根據已知原子的坐標確定坐標系原點.a 的坐標為(0,0,0),此為坐標原點.
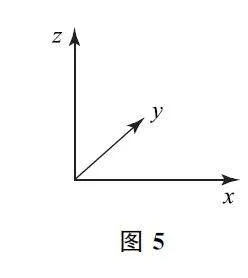
第2步:建立三維坐標系.根據已知信息,可以確定三維坐標系模型如圖5所示.
第3步:從原子所在位置分別向x、y、z 軸作投影,所得坐標軸上的截距即為該原子的分數坐標.根據d 的位置,可知其坐標參數為(1,1/2,1/2).
4 考查晶胞空間利用率
對于空間利用率的求解過程,解題思路如下:
第1步:根據“均攤法”確定晶胞中的微粒個數.
第2步:根據原子半徑計算所有微粒的體積.
首先要知道每個微粒(如原子或分子)的半徑.將每個微粒視為球形(對于原子而言),我們可以利用公式4πr2/3 來計算單個微粒的體積(r 代表微粒的半徑),將單個微粒的體積乘以晶胞中的微粒個數,就可以得到晶胞中所有微粒所占據的總體積.
第3步:根據晶胞參數或晶胞密度計算晶胞體積.
第4 步:根據公式計算.(空間利用率=晶胞占有的微粒體積/晶胞體積×100%)
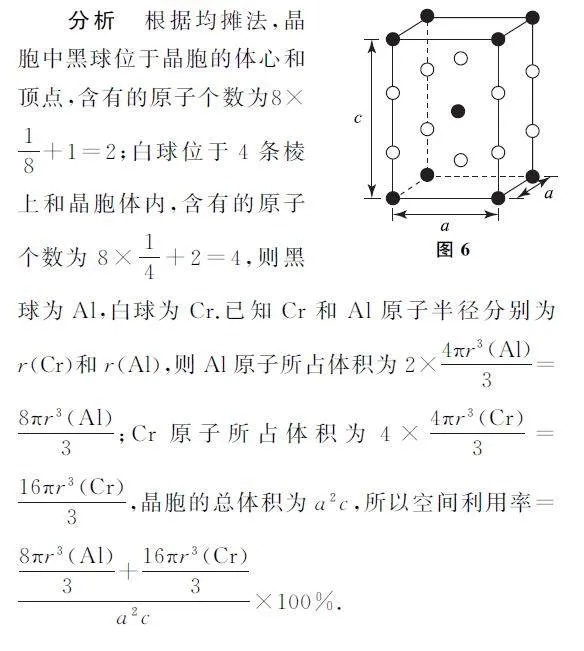
例4 AlCr2 具有體心四方結構,如圖6所示,設Cr和Al原子半徑分別為r(Cr)和r(Al),則金屬原子空間占有率為%___(列出計算表達式).
5 考查晶胞結構的投影圖
原子的投影問題是最近幾年試題中較新的考點,近5年高考中都有相應的考查.由于需要一定的空間想象能力和推斷能力,所以也提升了晶體結構知識考查的難度.此類題有“升維”和“降維”兩種考法.“降維”是以晶胞圖為基礎,通過觀察三維圖像,在三維坐標內進行投影.考查的知識點類似于數學中的“三視圖”,是數學中的立體幾何知識滲透化學知識的具體呈現形式.“升維”是以投影圖為基礎,利用投影圖去分析晶胞的三維結構,通過原子在某個平面上的投影,確定原子在空間的位置.
晶體結構與性質的考點,可歸結為兩大類,一是數目問題,如微粒的個數、化學式、晶體的密度以及空間利用率計算等;二是結構問題,如配位數問題、分數坐標、晶胞投影、晶胞空隙等.數目問題主要考查的是晶體結構中微粒的個數和分布,以及如何根據這些信息推導出晶體的化學式和密度.對于這類問題,通常需要使用“均攤法”,即將晶胞中的微粒按照其在晶胞中的分布情況均攤到每個晶胞中,從而得到每個晶胞的微粒數目,進而計算出晶體的化學式和密度.結構問題則主要考查的是晶體結構的形狀和構造,需要對晶體結構有深入的理解和分析能力,從結構入手,厘清常見晶體的結構,建立晶胞相關計算的思維模型,才能輕松應對考題.
(完)

