提升橫向磁通感應加熱均勻性的參數設計方法研究

摘要：金屬板材及復雜幾何鋼結構零件熱處理工藝的開發時間和成本與良好的仿真預測緊密相關，精準的參數設計可以提升熱處理的工藝水平。基于對磁導率的特性分析，提出了一種將復合磁導率視為材料物理特性的參數設計方法，實現了橫向磁通感應加熱均勻性精度的提高，依據重制擴散方程系統的算法，建立了功率等效模型，對復雜非線性復合磁導率進行了求解，通過設置仿真對比模型，驗證理論分析的正確性和可行性。

關鍵詞：電磁場;橫向磁通感應加熱;復合磁導率;功率等效模型;均勻性

中圖分類號：TM924.01 文獻標志碼：A 文章編號：1671-0797（2024）18-0080-05

DOI：10.19514/j.cnki.cn32-1628/tm.2024.18.020

0 引言

金屬材料的熱處理已經成為感應加熱技術的重要應用，在金屬薄板熱處理中，橫向磁通感應加熱技術具有比縱向磁通感應加熱技術加熱頻率更低、無功功率更小、效率更高等優點[1]。在金屬熱處理的應用中，衡量橫向磁通感應加熱效果優劣的最重要指標是加熱器出口處溫度分布的均勻性，但現有的傳統橫向磁通感應加熱技術普遍存在加熱器出口處溫度分布不均勻的缺陷，嚴重影響熱處理效果[2]。

目前對提高均勻性的研究分為兩大類：第一類是對感應加熱裝置進行研究，如改變加熱器結構和加熱線圈結構;第二類是對感應加熱數值分析技術進行研究，如采用磁熱耦合技術和靈敏度分析。其中感應加熱數值分析技術方面受到了國內外學者的廣泛關注，文獻[3]提出在使用三維仿真代碼進行數值模擬的同時應外加自動優化技術，即將遺傳算法與橫向磁通感應加熱系統的三維電磁與熱分析結合，提高系統的運行效率;文獻[4]提出對相同加熱器結構在ANSYS中開發多種數值模型結構，建立不同問題導向模型的實例，采用三維視角考慮對流和輻射對工件表面熱損失的影響，提出了新的加熱器參數計算方法并進行了熱力學分析;文獻[5]提出基于改進粒子群算法對電磁感應線圈進行多目標優化，提升了收斂速度，縮短了仿真時間，同時避免了優化過程陷入局部最優。這些方法可以用簡單的數值軟件進行模型解析，但是系統仿真的準確度嚴重依賴有限元模型（FEM）。因此，在金屬板材熱處理的工藝中選擇良好的仿真預測技術和正確的材料屬性對提升熱處理工藝水平至關重要[6]。

金屬板材作為一種鐵磁性材料，其磁感應強度-磁場強度曲線（B-H曲線）是高度非線性和磁滯的。此外，在時諧電磁場范疇，對金屬板材進行熱處理通常外加遠遠超過材料飽和程度的磁場振幅的激勵，這就導致了磁導率μ這種材料屬性難以確定。因此，研究金屬熱處理過程中的磁導率有十分重要的意義[7]。本文通過建立功率等效模型，采用重制擴散方程系統算法對復雜非線性復合磁導率進行求解;此外，通過參數設計、建立仿真模型對磁導率特性進行仿真分析，仿真結果表明，該方法能夠實現橫向磁通感應加熱均勻性精度的提升。

1 磁導率特性分析

時諧電磁場中磁感應強度、磁場強度只包括精確的單次諧波，在金屬板材熱處理過程中，如果達到溫度飽和點，材料的激勵信號、磁響應中的任何失真都不能很好地近似，這便導致了頻率截斷和間接耦合，不可避免地導致局部磁導率恒定。所以，只要獲得金屬板材在某非線性瞬變局部的功率分布，便可推導出磁導率與磁感應強度和磁場強度的關系。

采用特定的磁感應強度和磁場強度特性建立的磁導率磁阻模型雖然可以近似非線性無滯回材料和特定情況下的滯回材料，但由于一個周期內磁感應強度和磁場強度的振幅和平均值是給定的，且不直接成比例，不適用于局部功率損耗的計算。所以，為了減小磁導率的誤差，應以熱處理過程中的功率等效為基礎，最常用方法是采用經典的磁共能等效模型分析熱處理過程中的功率損耗[8]。

1.1 磁共能等效模型比較

磁共能不是一個實際存在的物理量，是一個具有能量量綱的非物理量。起始磁化線與主磁滯回線在磁場振幅較低的情況下差別很大，但是在金屬板材熱處理過程中，由于外加激勵產生的磁場振幅遠高于材料的磁飽和度，所以二者差別不大[9]。

平均磁導率與磁共能之間的關系可表示為：

μeq（H）= （1）

式中：μeq（H）為平均磁導率函數;（H）為復合角頻率函數;H為磁場強度。

磁共能等效模型可分為磁通密度共能等效模型、磁共能模型、增強磁共能模型，因增強磁共能模型損耗的磁共能是磁通密度共能等效模型與磁共能模型之和的平均值且兼具二者優勢，故采用增強磁共能模型作為對比模型。

1.2 磁導率數學模型

在橫向磁通感應加熱系統對金屬板材進行熱處理時，由圓環效應可知，加熱器出口處溫度分布在金屬板材的表面。在對磁導率進行功率等效時，因為在透熱深度一定的情況下，幾何效應和熱退磁效應對金屬板材表面上磁場擴散的影響可忽略不計，即在時域電磁場中，單位時間內金屬板材上的功率損耗完全由磁感應強度和磁場強度曲線決定，所以平均功率損耗的值為非線性磁滯的B-H曲線對應點瞬態值的疊加[10-11]。

在時域電磁場中，以非線性磁滯的B-H曲線作為基準，磁場強度為自變量，磁感應強度為因變量并給定足夠大的周期，采用有限元算法，構建平均功率密度并將其作為參考損耗，如式（2）所示：

ρ

+jω

（H）

（x，t）=0，x∈[0，t]，

H（0，t）=H0，

=0 （2）

式中：ρ為瞬態電阻率;H（x，t）為磁場強度函數;ω為角頻率;（H）為復合磁導率函數;（x，t）為復合磁場強度函數;H（0，t）為因變量為0時的磁場強度函數;H0為初始磁場強度。

由坡印廷定理可知，所有幾何物體在電磁場的作用下，其閉合曲面的坡印廷矢量的外法向分量的曲面積分值為曲面體積內含有的電場能與同體積磁場能轉化為熱能耗散的差值。在時域電場中，功率密度可表示為：

P（x，t）=-[E（x，t）×H（x，t）] （3）

式中：P為功率密度;為梯度算子;E為電場強度。

為了得到金屬板材熱處理表面的局部功率密度，利用安培定律和法拉第電磁感應定律，將電場轉化為磁場，式（3）進行改寫后取功率密度，并在整個周期內取平均值，可表示為：

P（x）=ρ

+H（x，t）

dt （4）

式中：T為周期;B（x，t）為磁感應強度函數。

由式（4）可以看出，非線性和磁滯材料的功率等效磁導率模型功率密度由兩部分組成：渦流損耗和磁滯損耗，但二者并未完全分離。磁感應強度B與磁場強度H相等時，第二項的積分為零。

因為電場和磁場同時存在，其角頻率ω可改寫為向量形式：

H（x，t）=（x）ejωt （5）

式中：（x）為磁場強度的幅值函數。

將式（3）與（5）聯立，式（4）可進一步改寫：

P（x）=

2+<E：＼2024＼機電信息202418＼機電信息202418＼2024-9機電正文＼趙佳成.jpg>

*（x） （6）

式中：<E：＼2024＼機電信息202418＼機電信息202418＼2024-9機電正文＼趙佳成.jpg>為函數實部;*（x）為磁場強度幅值函數的導數。

將式（6）改寫為關于自變量x的函數，其中<E：＼2024＼機電信息202418＼機電信息202418＼2024-9機電正文＼趙佳成.jpg>為實部，<E：＼2024＼機電信息202418＼機電信息202418＼2024-9機電正文＼趙佳成-1.jpg>為虛部。引入局部恒定復合磁導率的復數形式：

（x）=<E：＼2024＼機電信息202418＼機電信息202418＼2024-9機電正文＼趙佳成.jpg>

（x）+<E：＼2024＼機電信息202418＼機電信息202418＼2024-9機電正文＼趙佳成-1.jpg>

（x） （7）

ρ+jω（x）（x）=0 （8）

將式（7）與（8）聯立，平均功率密度為：

P（x）=

2-<E：＼2024＼機電信息202418＼機電信息202418＼2024-9機電正文＼趙佳成-1.jpg>（μ（x））|（x）|2 （9）

式（9）與式（4）相比，可以看出，兩式形式相似，平均功率密度也有兩個部分，由虛部可以看出，平均功率密度中的磁滯損耗與磁導率有關，即來自于磁場強度和磁感應強度相位差的磁導率引入，將平均功率損耗徹底分解成了渦流損耗和磁滯損耗兩個部分。金屬板材作為一種鐵磁性材料，在對其進行熱處理過程中金屬表面平均功率損耗由渦流損耗和磁滯損耗兩個部分組成，其中Peddy為渦流損耗，Physt為磁滯損耗，分別可表示為：

Peddy（x）=

2 （10）

Physt（x）=-<E：＼2024＼機電信息202418＼機電信息202418＼2024-9機電正文＼趙佳成-1.jpg>（μ（x））|（x）|2 （11）

由式（10）（11）可以看出，磁場強度向量決定渦流損耗大小，磁場強度向量和磁導率決定渦流損耗大小。磁導率由式（7）的實部、虛部表示，解耦后方程可表示為：

Peddy（x）=

2+H2

2 （12）

式中：?為相位。

Physt（x）=-<E：＼2024＼機電信息202418＼機電信息202418＼2024-9機電正文＼趙佳成-1.jpg>（μ）H2 （13）

此時，平均功率損耗可改寫為：

P=

+

2 （14）

該方程可以利用式（2）的邊界條件用有限元法求解。將式（12）（13）聯立，磁導率實部、虛部的表達式為：

<E：＼2024＼機電信息202418＼機電信息202418＼2024-9機電正文＼趙佳成.jpg>

（x）=

+

（15）

-

2 （16）

可以得到，磁導率中只有一個未知數H（x），即磁場強度H的大小。由于求解出來的常微分方程是非線性的，對其進行迭代計算需要迭代法和初始設定值H0（x）。通過牛頓迭代法，同樣以式（2）為邊界條件，在迭代過程中第δ次求解修正的磁場強度H將具有齊次邊界條件性質，使磁場強度H的初始值在定義域迭代時處處單調收斂，使磁場Hi（x）隨迭代次數的增加而更加準確，即在進行第i次迭代后，下一個磁場振幅的值為Hi+1（x）=H（x）+δH（x）。

1.3 磁導率分析

由上述推導可知，利用功率等效模型求解的磁導率是個復數，其實部和虛部具有對偶性，下文稱之為復合磁導率，表達式為：

（x）=

+

+

j

-

2 （17）

由式（17）可以看出，在金屬板材熱處理過程中，在激勵相位一定時，隨著外加的磁場振幅的增大，磁導率也會增大，但增大的趨勢不可得知。因為金屬板材在熱處理過程中其表面的等效功率損耗由渦流損耗和磁滯損耗兩個部分組成，在對功率等效求解的過程中引入了非線性復合磁導率，通過反解推導得之，所以在功率等效模型下磁導率的唯一邊界條件是橫向磁通感應加熱系統的外加磁場。

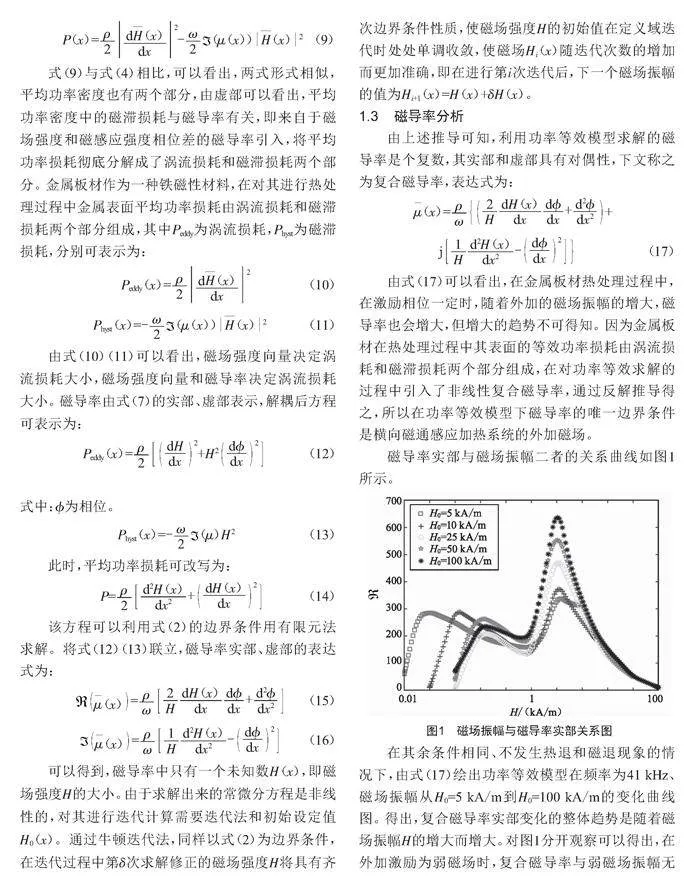
磁導率實部與磁場振幅二者的關系曲線如圖1所示。

在其余條件相同、不發生熱退和磁退現象的情況下，由式（17）繪出功率等效模型在頻率為41 kHz、磁場振幅從H0=5 kA/m到H0=100 kA/m的變化曲線圖。得出，復合磁導率實部變化的整體趨勢是隨著磁場振幅H的增大而增大。對圖1分開觀察可以得出，在外加激勵為弱磁場時，復合磁導率與弱磁場振幅無規律可循，原因是在熱處理過程中，弱磁場激勵對金屬板材磁導率的變化影響并不明顯。在外加激勵為中等強度磁場時，復合磁導率與磁場振幅呈現出正相關的趨勢。在外加激勵為較強磁場時，復合磁導率隨著磁場振幅的增大變化逐漸變小呈收斂趨勢，即一旦金屬板材達到飽和狀態，便會發生退磁現象，復合磁導率變化不明顯。

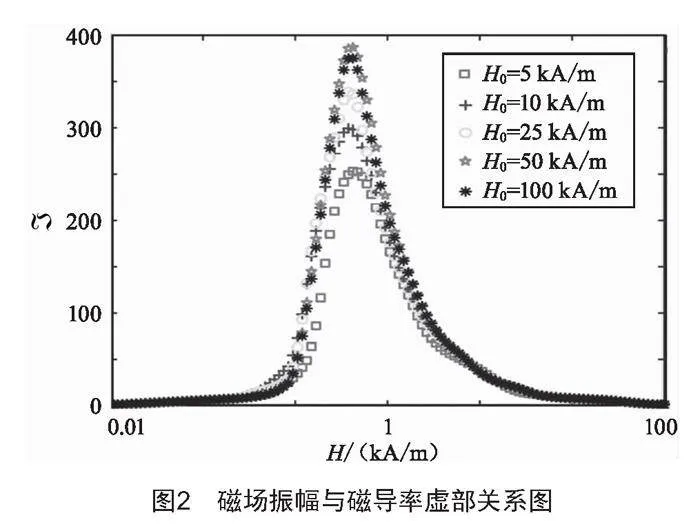
磁導率虛部與磁場振幅二者的關系曲線如圖2所示。

通過整體觀察圖2可得，復合磁導率虛部變化的整體趨勢是隨著磁場振幅H的增大而增大，但增大的趨勢并沒有實部明顯。圖2中通過觀察每條曲線可得，在外加激勵為弱磁場和強磁場時，變化關系同實部一樣，金屬板材磁導率的變化并不明顯。在外加激勵為中等強度磁場時，復合磁導率與磁場振幅呈現出正相關的趨勢。結論和磁場振幅與復合磁導率實部關系一致。

綜上所述，復合磁導率隨著磁場振幅H的增大而增大，飽和后復合磁導率的變化與磁場振幅H的增大關系不明顯，即在金屬板材熱處理過程中，板材飽和前復合磁導率為非線性，飽和后可認定為常數。將復合磁導率作為材料物理參數代入仿真器中，可以減小仿真與實際的誤差。

2 仿真驗證

2.1 仿真模型建立

為驗證將復合磁導率作為金屬板材的物理參數對金屬板材熱處理的仿真精度有所提升，本文設置增強磁共能和功率等效兩種仿真模型。其中功率等效模型設置兩組對比模型，一組將金屬板材的磁導率設置為常用的200 H/m，其他參數不變，由式（17）計算得另一組設置為191 H/m。將增強磁共能模型作為對照組，分別與兩組不同磁導率的功率等效模型的磁仿真結果進行對比。

在ANSYS Maxwell中建立雙正六邊形線圈的結構進行橫向磁通感應加熱器的模擬，正六邊形線圈下方設置為被加熱的金屬板材，尺寸為200 mm×400 mm×100 mm;設定感應加熱的發射線圈在外部，正六邊形發射線圈邊長為100 mm，是繞線匝數為27匝的螺旋線圈;中繼線圈在內部，正六邊形的中繼線圈邊長為78 mm，是繞線匝數為16匝的螺旋線圈。

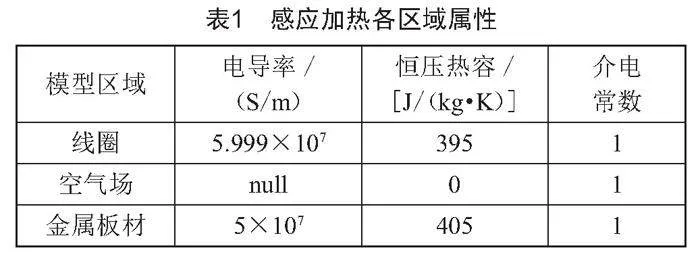
感應加熱各區域的單元類型和材料屬性具體參數如表1所示。

在ANSYS Maxwell中建立雙正六邊形線圈結構橫向磁通感應加熱器的仿真模型，如圖3所示。

將金屬板材常用的磁導率200 H/m設置為基準，對兩種磁導率模型進行磁場仿真并相互比較，用以驗證將計算出的復合磁導率視為材料物理特性有助于提升橫向磁通感應加熱均勻性精度的理論推導。

2.2 仿真結果分析

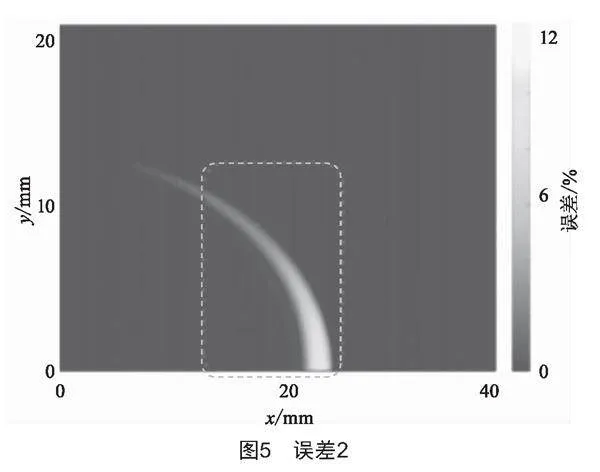
以增強磁共能等效模型作為基準，分別對磁導率為200 H/m的功率等效模型和磁導率為191 H/m的功率等效模型做誤差分析，分別稱為誤差1和誤差2，如圖4、圖5所示。

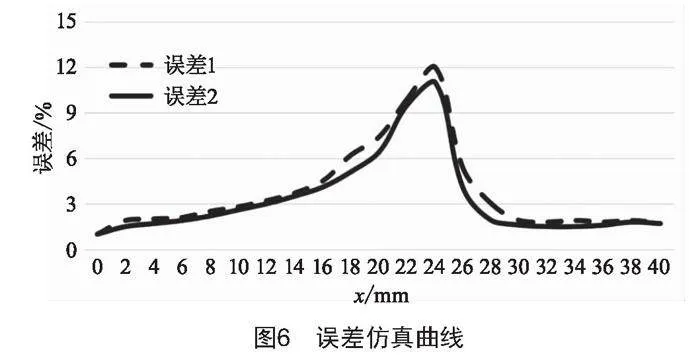
將圖4、圖5的誤差導出，繪制為曲線圖，如圖6所示。

由圖6得，誤差1的整體誤差值大于誤差2，前者最大誤差為12%，誤差平均值約為3.7%;后者最大誤差為11%，誤差平均值約為3.2%。

本文將磁通密度分布云圖作為衡量熱處理效果的依據，采用誤差分析、繪出誤差曲線的分析方法，得出后者更適合作為金屬板材熱處理仿真模型，驗證了將復合磁導率視為材料物理特性有助于提升橫向磁通感應加熱均勻性精度的結論。

3 結論

本文基于橫向磁通感應加熱在金屬板材熱處理中工藝水平精度不高的問題，提出了一種將復合磁導率視為材料物理特性的參數設計方法，并依據重制擴散方程系統的算法，建立功率等效模型，對復雜非線性復合磁導率進行了求解。最后通過參數設計進行了仿真模型建立和仿真分析，對理論分析進行了驗證，實現了熱處理過程中工藝水平精度的提高，驗證了理論的正確性和可行性。

[參考文獻]

[1] 盧華，胡金剛，畢闖，等.基于中心抽頭變壓器的倍頻感應加熱電源[J].電工技術學報，2016，31（24）：188-194.

[2] ALOTTO P，SPAGNOLO A，PAYA B.Particle swarm optimi-zation of a multi-coil transverse flux induction heating system[J].IEEE Transactions on Magnetics，2011，47（5）：1270-1273.

[3] MANNANOV E，GALUNIN S，BLINOV K.Numerical optimi-zation of transverse flux induction heating systems[C]// 2015 IEEE NW Russia Young Researchers in Electrical and Electronic Engineering Conference（EIConRusNW），2015：241-244.

[4] BLINOV K，GALUNIN S，NIKANOROV A，et al.Dynamics of electrothermal processes for cut or welded strips in tWnouWKcHEkFM4nu0tR+sUw==he induction through-heaters[C]// 2016 IEEE NW Russia Young Researchers in Electrical and Electronic Engineering Conference （EIConRusNW），2016：508-512.

[5] 房紫璐.電磁感應加熱線圈的多目標優化研究[D].杭州：浙江大學，2021.

[6] WANG J，LIN H Y，FANG S H，et al.Linear representa-tion of saturation characteristics associated with eddy currents in ferromagnetic materials[J].IEEE Transactions on Magnetics，2014，50（2）： 121-124.

[7] CHEN Q，XU B A，YI Y，et al.Secular simulation for dynamics of charged particles in the vortex electromagnetic wave beam[C]// 2016 IEEE MTT-S International Conference on Numerical Electromag-netic and Multiphysics Modeling and Optimization（NEMO），Beijing，China，2016：1-2.

[8] 許京荊.ANSYS 13.0 Workbench數值模擬技術[M].北京：中國水利水電出版社，2012.

[9] CHENG Y H，SHU Y M.A new analytical calculation of the mutual inductance of the coaxial spiral rectangular coils[J].IEEE Transactions on Magnetics，2014，50（4）：1-6.

[10] RAJU S，WU R X，CHAN M S，et al.Modeling of mutual coupling between planar inductors in wireless power applications[J].IEEE Transactions on Power Electronics，2014，29（1）：481-490.

[11] TANG Y，WANG Y，HONG S，et al.Research on electro-magnetic simulation of the electromagnetic heating roller[C]// Electronic and Automation Control Conference（ITNEC），2023：243-248.

收稿日期：2024-05-20

作者簡介：趙佳成（1998—），男，江蘇徐州人，助教，研究方向：感應加熱電源技術。

基金項目：西安鐵路職業技術學院2024年度立項課題“基于橫向磁通感應加熱技術的鋼軌正火均勻性精度研究”（XTZY24K08）