AGCFN:基于圖神經網絡多層網絡社團檢測模型

摘 要：基于圖神經網絡的多層網絡社團檢測方法面臨以下兩個挑戰。一是如何有效利用多層網絡的節點內容信息，二是如何有效利用多層網絡的層間關系。因此，提出多層網絡社團檢測模型AGCFN（autoencoder-enhanced graph convolutional fusion network）。首先通過自編碼器獨立提取每個網絡層的節點內容信息，通過傳遞算子將提取到的節點內容信息傳遞給圖自編碼器進行當前網絡層節點內容信息與拓撲結構信息的融合，從而得到當前網絡層每個節點的表示，這種方法充分利用了網絡的節點內容信息與拓撲結構信息。對于得到的節點表示，通過模塊度最大化模塊和圖解碼器對其進行優化。其次，通過多層信息融合模塊將每個網絡層提取到的節點表示進行融合，得到每個節點的綜合表示。最后，通過自訓練機制訓練模型并得到社團檢測結果。與6個模型在三個數據集上進行對比，ACC與NMI評價指標有所提升，驗證了AGCFN的有效性。

關鍵詞：多層網絡；社團檢測；圖神經網絡；自編碼器；自監督學習

中圖分類號：TP301.6 文獻標志碼：A 文章編號：1001-3695（2024）10-007-2926-06

doi：10.19734/j.issn.1001-3695.2024.03.0056

AGCFN： multiplex network community detection model based on graph neural network

Chen Long1a， Zhang Zhenyu1b， Li Xiaoming2， Bai Hongpeng3

（1. a.College of Software， b.College of Information Science & Engineering， Xinjiang University， rümqi 830000， China; 2.College of International Business， Zhejiang Yuexiu University， Shaoxing Zhejiang 312000， China; 3.College of Intelligence & Computing， Tianjin University， Tianjin 300000， China）

Abstract：Multiplex network community detection methods based on graph neural network face two main challenges. Firstly， how to effectively utilize the node content information of multiplex network; and secondly， how to effectively utilize the interlayer relationships in multiplex networks. Therefore， this paper proposed the multiplex network community detection model AGCFN. Firstly， the autoencoder independently extracted the node content information of each network layer and passed the extracted node content information to the graph autoencoder for fusing the node content information of the current network layer with the topology information through the transfer operator to obtain the representation of each node of the current network layer， which made full use of the node content information of the network and the topology information of the network. The modularity maximization module and graph decoder optimized the obtained node representation. Secondly， the multilayer information fusion module fused the node representations extracted from each network layer to obtain a comprehensive representation of each node. Finally， the model under went training， and it achieved community detection results through a self-training mechanism. Comparison with six models on three datasets demonstrate improvements in both ACC and NMI evaluation metrics， thereby va-lidating the effectiveness of AGCFN.

Key words：multiplex network; community detection; graph neural network; autoencoder; self-supervised learning

0 引言

現實生活中許多復雜的系統都可以抽象成一個網絡，如社交網絡［1］、學術合作網絡［2］、商品推薦網絡［3］等。網絡的一個顯著特征就是它們的社團結構。社團檢測研究目標是將網絡劃分成為不同的社團結構，同一個社團中的節點具有相似的特征或功能。當前有許多社團檢測方法被提出，但它們大多數僅適用于單層網絡［4，5］。然而實際上，很多網絡通常由多個層次組成，每一個層次都反映了網絡中不同類型的關系［6］。比如，在引文網絡中，兩篇論文的連接可以是不同類型的，如兩篇論文因為同一個作者而連接，或兩篇論文因為引用關系而連接［2］。在電影網絡中，兩個電影可以因為有共同的演員相連，也可以因為是共同的導演相連。這兩個網絡都可以分成兩個層次，在兩個層次中，節點是相同的，而節點之間的邊是不同的。

許多文獻提出了不同的社團檢測方法，如文獻［7，8］，這些方法通過將多層網絡合并為一個單層網絡，然后使用單層網絡社團檢測方法來發現社團結構。然而這類方法忽略了多層網絡的層間關系。比如在引文網絡的引用層中，僅知道論文的引用關系不能很好地將它們進行社團劃分，但是如果這些論文在另一個層次中有通過作者相連接，則確定這些論文的主題就會變得容易，因為作者的研究方向通常是確定的。因此，為了克服這個問題，文獻［10～12］進行了新的研究，將多層網絡層間關系進行提取，然而這類方法沒有利用網絡中豐富的節點內容信息。以引文網絡為例，如果利用論文中的關鍵詞，則對它們進行社團劃分也會變得容易［2］。文獻［2，12］利用了節點內容信息來進行多層網絡社團檢測，并取得了一定的成果。然而，受到圖卷積網絡層數的限制，這些方法在提取節點內容信息并將其與網絡拓撲結構信息融合方面存在一些不足之處。換言之，這些方法未能充分發揮網絡節點內容信息和拓撲結構信息的潛在優勢。因此，本文提出了一種能夠同時考慮多層網絡層間信息和節點內容信息的無監督多層網絡社團檢測模型AGCFN（autoencoder-enhanced graph convolutional fusion network）。

1 相關研究

目前主流多層網絡社團檢測方法集中于基于展平的方法、直接方法和基于聚合的方法［13］。

基于展平的方法的核心思想是采用基于權重的方式將多層網絡轉換為單層網絡的形式，然后在上面使用基于單層網絡的社團檢測方法來發現社團結構。文獻［7］將多層網絡展平為一個單層網絡，然后利用標簽傳播算法進行社團檢測，具體來說，它們使用一種新的目標函數和基于約束標簽傳播的優化策略來自動識別社團。文獻［8］提出了一種改進的粒子競爭模型，通過引入本地化度量，使模型可以正確確定社團數量。同時，該模型通過構建一個擴展鄰接矩陣來表示多層網絡，能夠很好地進行社團檢測工作。基于展平的方法簡單直觀，易于理解和實現，常常能夠使用單層網絡社團檢測方法的成果。然而這種方法忽略了不同層次的信息差異，可能導致對多層網絡中復雜關系的損失，不適用于包含豐富層次信息的網絡。

基于聚合的方法從多層網絡的每一個單一的層中提取信息，然后將其聚合成綜合的節點特征，以此來進行多層網絡的社團檢測工作。這類方法的核心思想是將多個網絡層上的信息進行整合，從而獲得更優的社團結構［9，10，12］。如文獻［9］提出一種用于多層網絡社團檢測的圖卷積融合模型GCFM，通過設計一個多尺度融合網絡，融合節點在不同層和不同尺度上的編碼來學習節點嵌入表示。文獻［12］提出了一種基于圖神經網絡的多層網絡社團檢測模型 MGCAE，首先引入互信息來對不同層的節點進行局部表示和全局表示，以此探索不同網絡層之間的關系。其次通過結合伯努利-泊松損失和模塊化最大化損失來共同優化原始鄰接矩陣的重建，最終得到更好的節點嵌入表示。

直接方法指的是直接在多層網絡上進行社團檢測的方法，這種方法同時對每個網絡層進行特征提取，從而檢測出社團結構。如文獻［14］將模塊度指標進行擴展，提出了新的模塊度指標QM，用于代替原本的模塊度最大化指標，使其可以適應多層網絡社團檢測。

上述方法對于多層網絡社團檢測都有推動作用，然而也存在著一些問題，如利用多層網絡的節點內容信息不充分、不能充分融合多層網絡層間信息等。

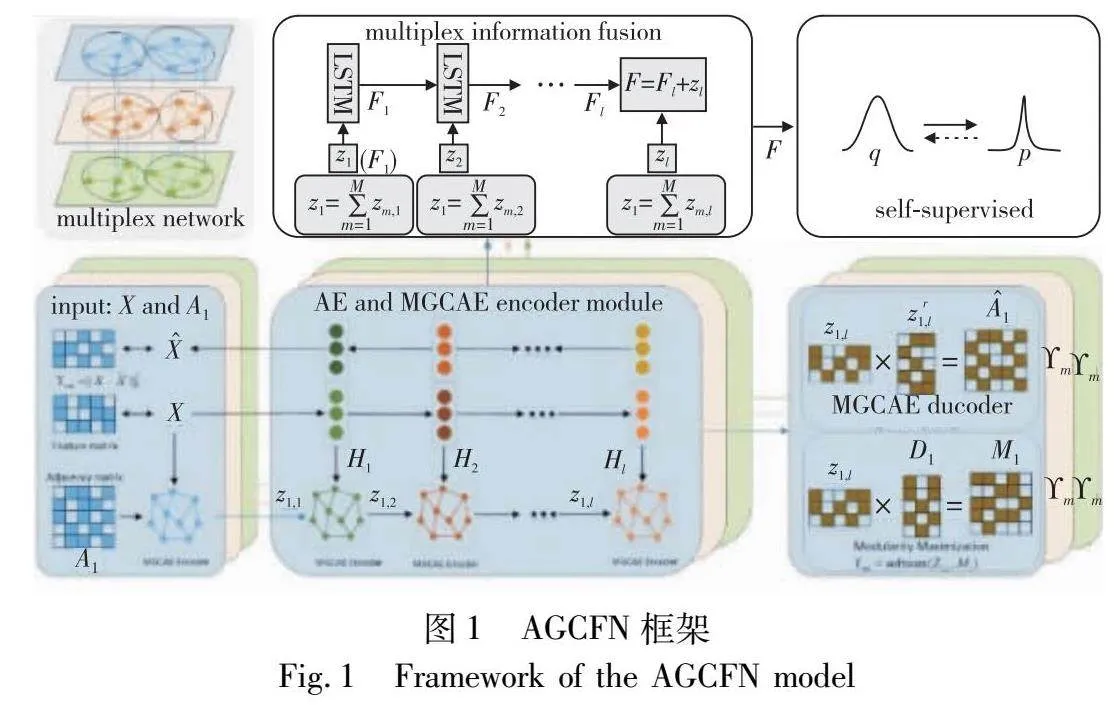
通過分析上述方法，本文提出了AGCFN模型。首先通過在多層網絡的每一層構建深度自編碼器模塊與圖自編碼器模塊MGCAE，獲得網絡中每個節點在每個網絡層的表示，使模型有效學習網絡的節點內容信息與拓撲結構信息；其次，通過模塊度最大化模塊對每個節點的表示進行優化，同時，MGCAE解碼器部分對提取到的節點表示進行重構，使其恢復到每個網絡層的鄰接矩陣的形式，對于獲取的每個網絡層的節點的表示，通過多層信息融合模塊MIF進行融合，得到每個節點的綜合表示；最后，通過自監督模塊將各個模塊統一在一個框架中，完成無須標簽信息的多層網絡社團檢測任務。

2 基于圖神經網絡的多層網絡社團檢測模型

2.1 問題定義

假定一個多層網絡G={G1，G2，…，GM}，其中Gm=（V，Em，X）。V={vi}i=1，…，N為具有N個節點的網絡的節點集合。Em={（vi，vj）|1≤i，j≤N，i≠j}為多層網絡第m個網絡層的邊集。X=［x1，x2，…，xN］為G的屬性，其中xi為vi的屬性。A={A1，A2，…，AM}為網絡鄰接矩陣的集合，Am=Euclid ExtraaBpN×N表示網絡第m層的鄰接矩陣。其中Amij=1表示節點vi與vj之間存在邊，否則Amij=0。

2.2 模型框架

本文模型AGCFN的框架如圖1所示。模型主要包含自編碼器模塊、多層圖卷積自編碼器模塊、模塊度最大化模塊、多層信息融合模塊和自監督模塊。

2.2.1 多層自編碼器模塊

雖然普通的圖卷積網絡可以自動融合節點內容信息與拓撲結構信息，但是這種融合僅僅將節點內容信息直接輸入到圖卷積網絡中與拓撲結構進行卷積，可能會使模型忽略節點內容信息中的細節部分，并且會使得圖卷積層數不能加深，容易出現過擬合問題。換言之，其對節點內容信息與拓撲結構信息利用不夠充分。為了充分利用節點內容信息，使用自編碼器對每個網絡層的節點內容信息進行提取。為了降低算法的復雜性，本文使用線性結構的自編碼器［15］。

在多層網絡中，節點的內容信息是一致的，而每一層的拓撲結構信息不同，因此對于每一個網絡層，本文都設置了自編碼器模塊用來提取內容信息，而后通過傳遞算子傳遞給對應的MGCAE層進行卷積操作。

假設多層網絡具有M個網絡層，每一個網絡層具有L個層次結構的自編碼器，則對于第m個網絡層的第l層自編碼器提取到的內容信息，可由下式得到：

H（）m=（W（）m，eH（－1）m+b（）m，e）（1）

其中：表示激活函數；W（）m，e和b（）m，e分別表示編碼器部分第層的權重矩陣和偏置。特別地，對于原始輸入，使用網絡的節點內容信息X。與編碼器對應的是解碼部分，公式如下：

H（）m=（W（）m，dH（－1）m+b（）m，d）（2）

其中：W（）m，d和b（）m，d分別表示解碼器部分第層的權重矩陣和偏置。第m個網絡層解碼器部分的輸出H（L）m=X^是對原始節點內容信息的重構，因此可以得到如下目標函數：

m，res=‖X－X^‖2F（3）

其中：‖·‖F表示矩陣的弗羅貝尼烏斯范數。因為多層網絡共有M個層，因此，關于節點內容信息重構的總損失為

res=∑Mm=1m，res（4）

通過優化該目標函數，可以使算法學習到更加優質的節點內容信息。

2.2.2 多層圖卷積自編碼器模塊

自編碼器能夠有效學習多層網絡的節點內容信息，但是卻不能利用網絡的拓撲結構信息。經典的圖卷積網絡在利用兩種信息上具有優勢，然而為了緩解圖卷積層不能加深導致模型提取不到更好的節點表示的問題，本節提出多層圖卷積自編碼器模塊MGCAE，通過傳遞算子將不同尺度自編碼器提取到的節點內容信息傳遞給對應的圖自編碼器層，以完成對多層網絡每個網絡層的節點內容信息與拓撲結構信息的聚合操作，使得模型可以捕捉到更加豐富的全局信息。

對于多層網絡第m個網絡層，MGCAE的編碼器第l層學習到的表示Z（）m可以通過下式得到：

Z（）m=（D－12mAmD－12mZ（－1）mW（－1）m）（5）

其中：表示激活函數；D－12mAmD－12m表示關于第m個網絡層的鄰接矩陣的規范化拉普拉斯矩陣；Am=Am+I表示第m個網絡層的鄰接矩陣加單位矩陣。為了將自編碼器學習到的對應層的節點內容信息也考慮進來，從而增強MGCAE的學習能力，使用傳遞算子將Z（－1）m和H（－1）m結合在一起。結合后的新的表示為

Z（－1）m=（1－ε）Z（－1）m+εH（－1）m（6）

其中：ε為平衡參數，其值設置為0.5。通過這種傳遞方法，將自編碼器與MGCAE逐層連接在一起。本文使用Z（－1）m作為第m個網絡層的MGCAE編碼器的第層的輸入，生成的表示Z（）m如下：

Z（）m=（D－12mAmD－12mZ（－1）mW（－1）m）（7）

特別地，對于每個網絡層的MGCAE的第一層的輸入，使用節點內容信息和當前網絡層的鄰接矩陣。

在MGCAE的解碼器部分，使用如下公式對得到的中間表示Z（）m進行重構，使其恢復成鄰接矩陣的形式：

A^m=sigmod（Z（L）m（Z（L）m）T）（8）

其中：A^m表示重構的第m層的鄰接矩陣。對于每個網絡層的重構損失，使用交叉熵損失函數：

m，adj=－1N∑Ni=1 ∑Nj=1［Am（ij）log（A^m（ij））+

（1－Am（ij））log（1－A^m（ij））］（9）

根據式（9），每個網絡層的MGCAE關于鄰接矩陣重構總損失為

adj=∑Mm=1m，adj（10）

2.2.3 多層信息融合模塊

對于多層網絡的每個網絡層，本文設計了自編碼器模塊與圖自編碼器模塊進行網絡節點內容信息與拓撲結構信息的融合，進而得到節點表示，并且自編碼器與圖自編碼器都是多尺度的，這樣就會得到每個節點在每個網絡層不同尺度的表示。又因為每個網絡層的鄰接矩陣都代表了不同的連接類型，所以每個網絡層得到的不同尺度的節點中間表示都是非常重要的。

為了將這些不同層不同尺度的中間表示進行融合，本文提出了一個多層信息融合模塊MIF。具體來說，對于一個具有M個網絡層的多層網絡，因為沒有先驗信息決定每個網絡層的重要程度，本文認為每個網絡層提取到的信息同等重要，所以每個網絡層的MGCAE的第層提取到的信息使用如下公式將它們進行融合：

Z（）=∑Mm=1Z（）m（11）

受到LSTM網絡的啟發，在得到了當前尺度的Z（）后，可以使用LSTM單元來整合不同尺度的F（），這樣做的好處是可以全面學習不同尺度的中間表示。此外，只有一個單元的LSTM結構還具有簡單高效的優勢。首先，將第一層的LSTM輸入設置為

F（1）=Z（1）（12）

其中：Z（1）為初始維度的表示。接下來，對于第l個維度的節點表示，將多尺度節點表示Z（－1）和F（－1）結合起來。使用如下公式進行計算：

F（）=LSTMCell（F（－1）+Z（－1））（13）

其中：LSTMCell表示的是LSTM單元。算法通過 LSTM 單元可以學到不同尺度特征之間的復雜關系，進而更好地融合這些信息。門控機制有助于模型選擇性地關注和保留重要的多尺度信息，避免梯度消失或爆炸的問題，同時提供更強大的建模能力。

對于MIF最后一層的計算，直接將Z（）和F（）進行加和操作。

F=F（）+Z（）（14）

2.2.4 模塊度最大化模塊

在多層網絡社團檢測模型中，模塊度是衡量社團結構的一個關鍵指標［16］，它衡量了網絡中節點的社團歸屬度與隨機網絡的差異程度。模塊度的最大化意味著將節點分配到不同的社團中，使得網絡的內部連接密集，社團之間的連接稀疏，從而達到社團結構的優化目標。

為了優化模型學習到的網絡節點嵌入表示，本文設計了一個多層模塊度最大化模塊，即為每個網絡層都使用模塊度最大化方法以確保節點嵌入保留了網絡的社團結構。具體而言，在每個網絡層都對圖解碼器部分重構的鄰接矩陣計算模塊度，以達到優化節點表示的目的。模塊度定義如下：

Q=14m∑ni， j（Aij－didj2m）（HiHTj）（15）

其中：di和dj表示節點vi和vj的度。通過定義模塊度矩陣B=［Bij］n×n，令Bij=Aij－didj2m，則有

Q=14m∑ni，j（Bij）（HiHTj）（16）

進一步化簡可以得到

m，Mod=Tr（HTmBmHm）（17）

其中：Tr（·）表示矩陣的跡且Tr（HTH）=N。H表示節點的社團歸屬度矩陣，它的每一行都可以看做是節點對應的嵌入表示。接下來將H進行歸一化，這樣的好處是可以在保留網絡社團結構的情況下得到更好的節點嵌入表示［17］。

由于與節點數量相比，社團的數量是非常少的，這種情況下如果以實際社團的個數作為嵌入維度，那么不足以學習到豐富的節點表示。因此，設計一個可學習的全連接層［4］。多層網絡第m個網絡層的模塊度最大化模塊損失可以表示為

m，Mod=Tr（HTmBmHm）（18）

其中：Hm=softmax（Z（）mC（）m）。最終關于模塊度最大化模塊總損失為

Mod=∑Mm=1Tr（HTmBmHm）（19）

2.2.5 自監督模塊

通過多層信息融合模塊，可以得到關于多層網絡中每個節點的最終表示，這個表示融合了每個網絡層的層內信息、層間信息和節點的內容信息。為了適應無標簽的任務，使用自監督模塊來進一步處理節點表示，并使用KL散度計算損失，用以指導算法自動更新。

首先，使用K-means算法尋找社團中心。確定社團中心后，對于第i個樣本和第j個社團，本文使用Student’S-T［18］分布來計算函數分布，公式如下：

qij=（1+‖fi－μj‖2/α）－α+12∑j′（1+‖fi－μj‖2）－α+12（20）

其中： fi表示節點最終表示F（L）的第i行；μj表示由自編碼器通過K-means方法得到的社團中心；α表示的是帶寬參數，本文設置α的值為1。為了提高檢測出社團的內聚性，使得最終表F在空間中的相似性更接近其所屬的社團中心，將Q進一步計算，得到分布P。計算公式如下：

pij=q2ij/kj∑j′q2ij′/kj′（21）

其中：kj=∑iqij。得到分布P后，使用KL散度來衡量P與Q之間的差距：

KL=KL（P‖Q）=∑i ∑jpijlogpijqij（22）

進一步將計算的所有損失進行統一，得到了算法的損失函數：

=res+adj－λMod+ηKL（23）

其中：λ和η為超參數。本文最終以分布Q來進行社團檢測，因為它包含了多層網絡的綜合信息。對于樣本i，分配給社團j的計算公式為

gi=arg maxj qij（24）

其中：qij由式（20）得到。

2.2.6 復雜度分析

AGCFN模型的復雜度主要取決于多層網絡的層數和MGCAE的層數。假設多層網絡的層數為M，MGCAE模塊深度為L，輸入數據的維度為d，網絡節點個數為N。自編碼器模塊的時間復雜度為O（Nd1d2…dL－1dLdLdL－1…d2d1），即O（Nd21d22…d2L）。MGCAE模塊編碼器的時間復雜度與鄰接矩陣的邊數|ε|呈線性關系，為O（|ε|d1d2…dL），解碼器的時間復雜度取決于網絡中節點的數量，為O（N）。模塊度最大化模塊的時間復雜度為O（N2）。對于多層信息融合模塊，使用的LSTM單元的時間復雜度也為O（Nd21d22…d2L）。自監督機制的時間復雜度為O（NM+Nlog N）。綜上所述，AGCFN的總時間復雜度為O（2Nd21d22…d2L+|ε|d1d2…dL+N2+NM+Nlog N）。

3 實驗結果與分析

3.1 數據集

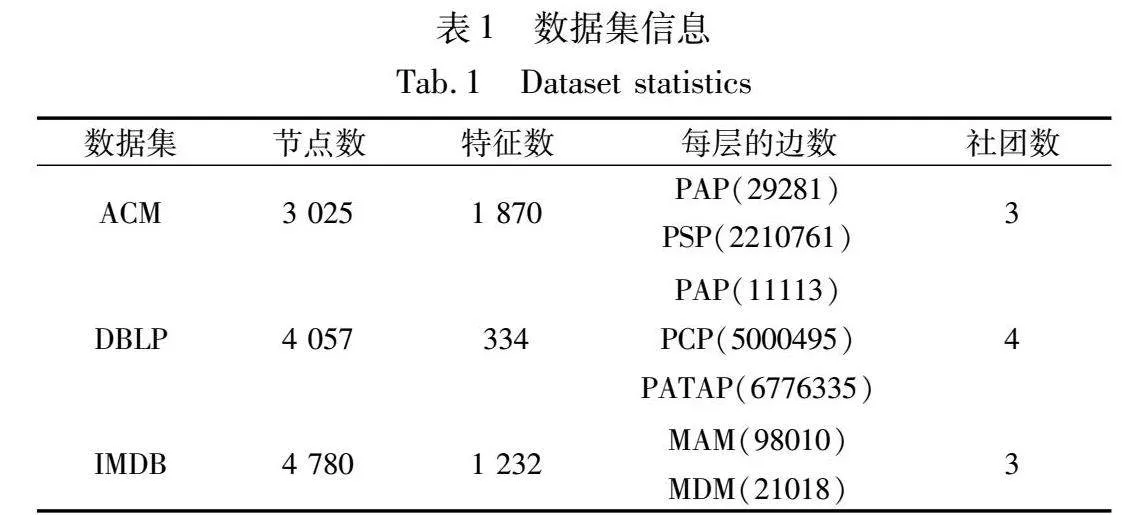
本文選取ACM、DBLP、IMDP三個數據集進行實驗。數據集的具體細節如表1所示。

ACM和DBLP數據集是引文網絡數據集，ACM數據集具有兩個層次，第一層中節點的連接關系為同一作者，第二層的連接關系為相同主題。它的目標是將論文分為數據庫、無線通信和數據挖掘三個社團。DBLP數據集的網絡有三個層次，在三層網絡中，節點之間的連接關系分別為同一作者、同一會議和作者所屬團隊。它的目標是將論文分為DM、AI、CV和NLP四個社團。IMDB數據集是一個關于電影網絡的數據集，它具有兩個層次，分別是通過相同導演相連接和通過相同演員連接。它的任務是將電影分為動作、喜劇和戲劇三個社團。

3.2 對比模型與評估指標

為了驗證AGCFN的性能，實驗將AGCFN與其他6個先進算法進行比較。GCFM［9］通過使用圖卷積網絡提取節點表示，而后將節點表示融合進行社團檢測。MGCAE［12］通過對多層網絡的節點拓撲結構信息進行增強，使用基于互信息的方式提取特征進行社團檢測。GEAM［10］通過構建層對比學習模塊，從每個網絡層的局部和全局圖視圖對節點和圖嵌入進行編碼，并提出一種自關注自適應融合機制，通過多層融合學習節點表示的綜合版本。GAE-avg［19］為GAE模型在多層網絡社團檢測的擴展。以上幾種方法為基于聚合的方法。PMNE［20］是直接方法，在每個網絡層上直接進行社團檢測。PwMC［21］為展平方法，是一種參數加權的多層網絡社團檢測方法。

對于社團檢測結果的評價指標，使用準確性度量（ACC）、歸一化互信息（NMI）這兩個廣泛使用的指標。ACC是衡量模型在社團檢測任務中預測結果與真實結果之間匹配程度的指標。它的高低直接反映了算法在檢測社團結構時的準確性和可靠性。NMI是衡量兩個分布之間相似度的指標，用于評估模型劃分的社團結構與真實社團結構之間的一致性程度。其取值為0～1，其結果越大表示檢測出的社團越貼近真實情況。

3.3 參數設置

本實驗配置為Windows 10操作系統，CPU型號為AMD EPYC 7542 32-Core Processor，內存204.8 GB，GPU類型為3090-24G。實驗使用Python 3.8開發環境。

實驗設置AGCFN的迭代次數為50輪，學習率為0000 1。對于AGCFN的自編碼器部分，進行20輪的預訓練。自編碼器模塊的維度設置為d－500－500－2000－30，MGCAE模塊的維度與自編碼器維度相同并將權重參數設置為0.5。

3.4 結果分析

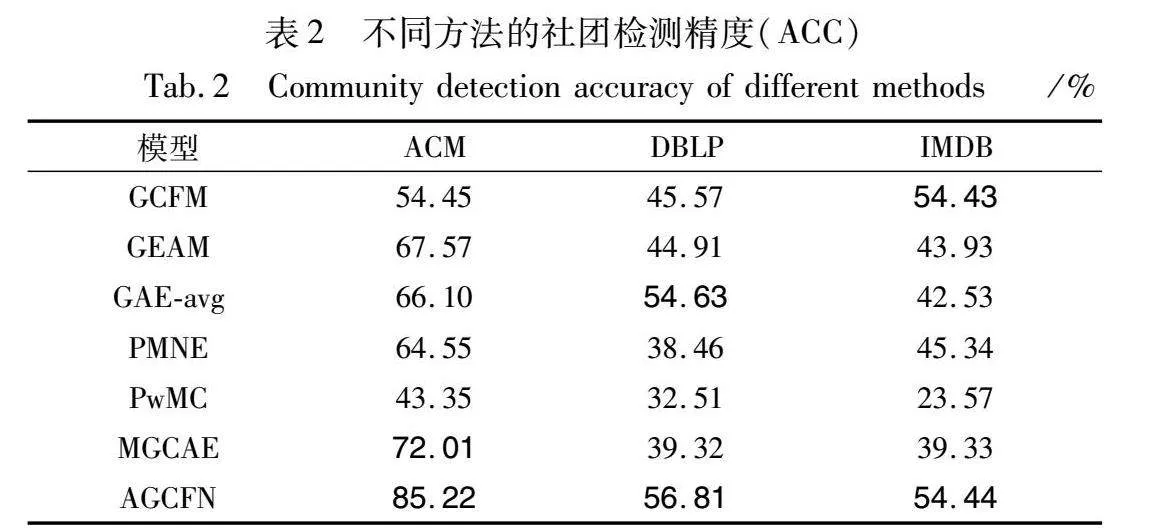
因為部分方法用到了K-means方法，所以會有實驗誤差，為了防止極端情況發生，將這些方法運行10次，取10次結果的平均值作為最終結果進行評價。表2和3展示了結果，其中最佳結果的前兩名使用加粗字體標識。

從表2可以得出結論：在三個數據集的實驗結果上，對于ACC評價指標，AGCFN優于所有其他方法；AGCFN具有很好的聚類性能，進行社團檢測時準確度很高；自編碼器學習到的節點內容信息成功傳遞給MGCAE模塊進行兩種信息的融合，并且多層信息融合模塊也得到了更優的節點綜合表示。自監督模塊成功地進行了反向傳播，使得模型表現出優勢。

通過表3可以得出：對于NMI評價指標，相較于除MGCAE方法外的最好方法，分別提高了12.27%，1.90%，041%。但是AGCFN表現次于MGCAE，這是因為AGCFN的各個模塊注重學習網絡中節點的嵌入表示并將其進行整合，這個過程會提高節點嵌入的準確性，但在計算社團檢測結果與真實社團匹配一致性程度上，MGCAE通過引入超圖的計算，選取每個網絡層的前k個最大連通子圖對拓撲結構信息進行了加強，所以其NMI指標高于AGCFN。本文算法沒有引入超圖的原因是計算超圖會使時間復雜度很高，影響算法的效率。

此外，值得注意的是，在IMDB數據集上，所有的方法在NMI指標上表現都不是很好。這是因為IMDB網絡中的節點之間的關聯信息比較分散，不具有很高的置信度。但是AGCFN依然能夠取得第二名的效果，說明聚合層間關系和考慮節點內容信息有助于社團檢測工作。

3.5 消融分析

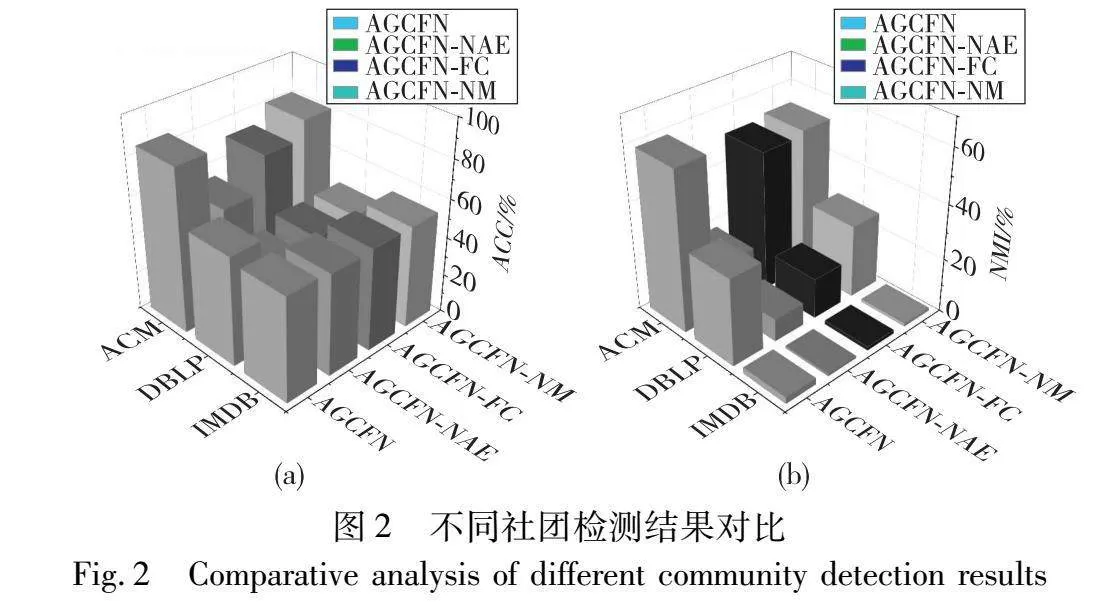
為了探究AGCFN模型中各個模塊的有效性，本節設計了消融實驗。具體來說，本次實驗設計了三個變體，分別為AGCFN-NAE 、AGCFN-FC 和AGCFN-NM 。AGCFN-NAE在AGCFN的基礎上，將AE自編碼器去除，不使用其獨立提取節點內容信息，用來探究節點內容信息對多層網絡社團檢測的影響。AGCFN-FC是為了探究多層網絡融合模塊的作用，本變體將其進行替換，不使用LSTM單元，只使用普通的全連接網絡［9］。AGCFN-NM則是將模塊度最大化模塊去除，用來探究模塊度最大化模塊對模型的影響。

對于每種變體，同樣使用ACC和NMI作為評價指標，使用三個數據集進行實驗，實驗結果如圖2所示。

圖2中，圖（a）表示不同變體社團檢測的精度，圖（b）為不同變體社團檢測的歸一化互信息，從中可以看出：在幾種變體中，AGCFN-NAE表現與其他幾種變體以及AGCFN相比性能最差。這說明了自編碼器模塊對模型的貢獻很大。自編碼器能夠有效學習多層網絡的節點內容信息，并通過傳遞算子傳遞給MGCAE模塊，這樣可以使模型有效學習多層網絡每一層的節點表示。AGCFN-FC的表現說明了本研究提出的多層融合模塊的重要性。將多層網絡每一個網絡層學習到的節點表示整合出來，并使用LSTM單元進行傳播與學習，能夠成功融合不同尺度的節點表示，最終得到一個優質的節點綜合表示。AGCFN-NM變體則體現出了模塊度最大化模塊的作用，表明模塊度最大化模塊有利于模型進行社團檢測工作。

3.6 運行時間與收斂性分析

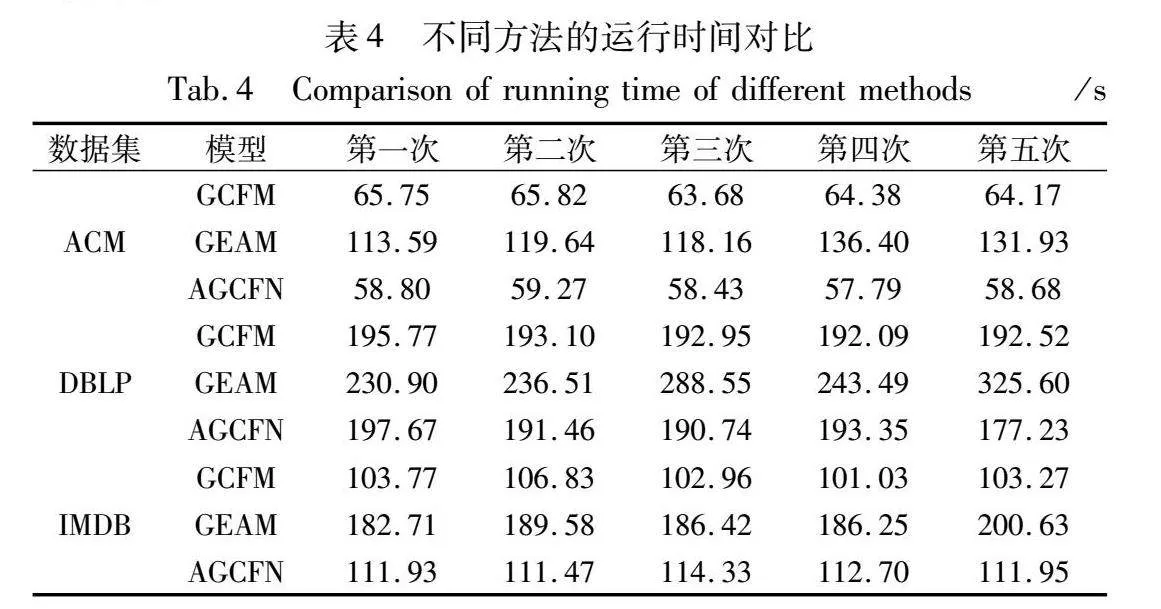
本節通過在三個數據集上進行實驗來對AGCFN算法的運行時間以及收斂性進行分析。因為實驗結果具有隨機性，本文在每個數據集上進行5次實驗。對于模型的運行時間，選擇GCFM、GEAM兩個模型與AGCFN進行對比，其對比結果如表4所示。

如表4所示，在ACM數據集上，GCFM、GEAM與AGCFN模型5次的運行平均時間分別為64.76 s、123.94 s、58.59 s；在DBLP數據集上分別為193.28 s、265.01 s、190.09 s；在IMDB數據集上分別為103.57 s、189.11 s、112.47 s。可以看出，AGCFN的運行時間與GCFM運行時間相近，說明AGCFN在具有較高精度的情況下，沒有付出過多的時間代價。而GEAM的運行時間較長是因為它的自關注與自適應融合機制需要進行大量計算。此外，可以看出，多層網絡的網絡層數與節點數量會影響模型的運行時間，這也從實驗角度驗證了本文的時間復雜度分析。

對于模型的收斂性，實驗結果如圖3所示，因為在實驗中模型收斂性差距很小，并且在IMDB數據集上的表現情況與ACM和DBLP數據集上的表現情況相近，所以為了避免冗余，圖3展示在ACM和DBLP數據集中進行兩次實驗的結果。

圖3中，每個子圖的橫坐標代表迭代次數，本節將最大迭代次數設置為50。縱坐標代表損失值。其中圖（a）和（b）為在ACM數據集上的實驗結果圖（c）和（d）表示在DBLP數據集上的實驗結果。從圖中可以看出，在兩個數據集上，隨著迭代次數的增加，損失函數逐漸減小并趨于穩定，雖然圖（c）具有一定波動性，但是在迭代20輪以后也可以很快趨近于固定值。因此可以從實驗角度得出，AGCFN模型是可以隨著訓練次數增加而快速收斂的。

3.7 超參數分析

為了探究超參數取值對模型的影響，本節設計了超參數實驗。對于式（23）提到的兩個用來度量KL散度損失和模塊度最大化模塊損失的超參數λ和η，對其敏感性進行分析。對于超參數λ，實驗設計它的取值為λ={0.1，0.3，0.5，0.7，09，10}。對于超參數η，設計它的取值為η={001，003，005，007，0.09，0.10}。實驗使用ACM數據集進行實驗，實驗結果如圖4所示。

從圖4中可以看出，AGCFN對自訓練模塊的KL損失的敏感度大于對模塊度最大化模塊的損失。但總的來說，AGCFN模型對超參數不敏感。實際中選擇兩個超參數λ和η的值分別為0.1和0.01。

4 實例分析

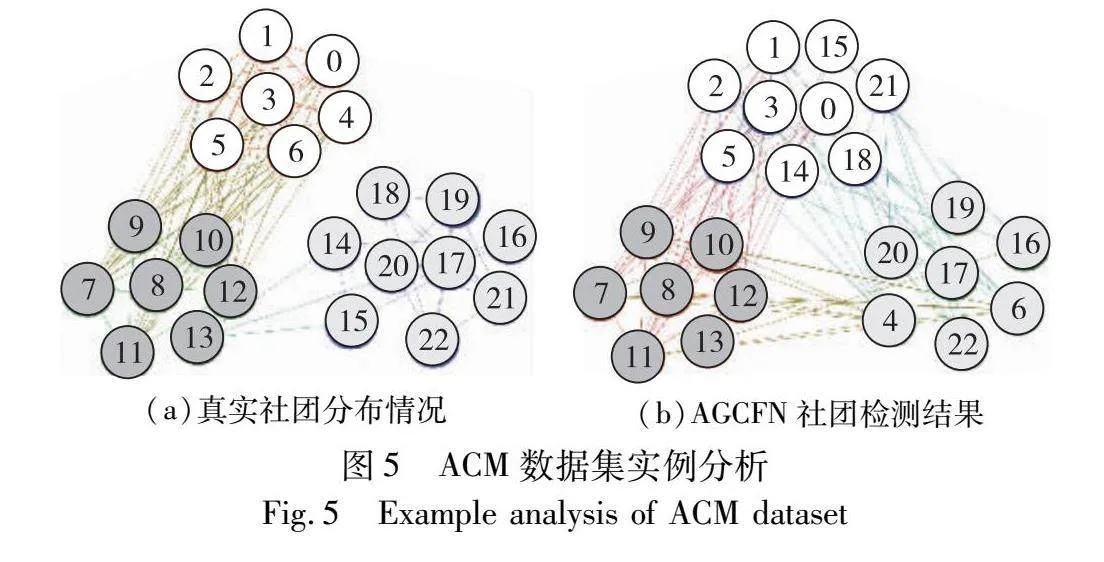
本章通過在ACM數據集上進行實例分析以展現AGCFN模型的有效性。具體而言，使用Gephi工具對AGCFN的社團檢測結果進行直觀展示，因為ACM數據集節點數量較多，為了更清晰地展現AGCFN的效果，從其三個社團分別隨機選取若干節點進行可視化。隨機抽取的節點編號分別為499，511，562，622，829，858，1023，1078，1143，1194，1382，1792，1803，1944，2230，2522，2540，2703，2754，2790，2897，2987，3014。為了直觀地展示與分析，將其進行重新編號，形成0～22號節點。社團檢測結果如圖5所示，其中（a）為真實社團情況，（b）為AGCFN社團檢測結果。依此驗證AGCFN模型的有效性。

5 結束語

本文提出了一個新的社團檢測模型AGCFN。通過構建自編碼器模塊、MGCAE模塊、多層信息融合模塊、模塊度最大化模塊和自監督模塊，使得模型能夠同時考慮多層網絡節點內容信息和層間信息。自編碼器模塊與MGCAE模塊配合進行每個網絡層的兩種信息提取；隨后多層信息融合模塊將其進行融合，得到每個節點的綜合表示；自監督模塊與模塊度最大化模塊用來進行損失度量，進而得到完整的損失函數，以完成模型的自訓練與收斂。最后通過實驗驗證了AGCFN模型及所提各個模塊的有效性。當前模型僅在中等規模數據集上進行了實驗，然而現實中存在節點規模龐大的數據集，未來工作將進一步研究分析，使模型適用于大規模節點的網絡。

參考文獻：

［1］宗傳玉， 李箬竹， 夏秀峰. 基于位置社交網絡的用戶社區和屬性位置簇搜索 ［J］. 計算機應用研究， 2023， 40（9）： 2657-2662. （Zong Chuanyu， Li Ruozhu， Xia Xiufeng. User community and attribute location cluster search in location-based social networks ［J］. Application Research of Computers， 2023， 40（9）： 2657-2662.）

［2］Park C， Kim D， Han J，et al. Unsupervised attributed multiplex network embedding ［C］// Proc of AAAI Conference on Artificial Intelligence. Palo Alto，CA：AAAI Press，2020： 5371-5378.

［3］馮興杰， 生曉宇. 基于圖神經網絡與深度學習的商品推薦算法 ［J］. 計算機應用研究， 2021， 38（12）： 3617-3622. （Feng Xingjie， Sheng Xiaoyu. Item recommendation algorithm based on GNN and deep learning ［J］. Application Research of Compu-ters， 2021， 38（12）： 3617-3622.）

［4］Zhou Xinchuan， Su Lingtao， Li Xiangju，et al. Community detection based on unsupervised attributed network embedding［J］. Expert Systems with Applications， 2023， 213： 118937.

［5］Berahmand K， Mohammadi M， Saberi-Movahed F，et al. Graph regularized nonnegative matrix factorization for community detection in attributed networks［J］. IEEE Trans on Network Science and Engineering， 2022， 10（1）： 372-385.

［6］Huang Xinyu， Chen Dongming， Ren Tao，et al. A survey of community detection methods in multilayer networks［J］. Data Mining and Knowledge Discovery， 2021， 35： 1-45.

［7］Boutemine O， Bouguessa M. Mining community structures in multidimensional networks［J］. ACM Trans on Knowledge Discovery from Data， 2017， 11（4）： 1-36.

［8］Gao Xubo， Zheng Qiusheng， Verri F A N，et al. Particle competition for multilayer network community detection ［C］// Proc of the 11th International Conference on Machine Learning and Computing. New York： ACM Press， 2019： 75-80.

［9］Cai Xiang， Wang Bang. A graph convolutional fusion model for community detection in multiplex networks［J］. Data Mining and Knowledge Discovery， 2023， 37（4）： 1518-1547.

［10］Wang Bang， Cai Xiang， Xu Minghua，et al. A graph-enhanced attention model for community detection in multiplex networks［J］. Expert Systems with Applications， 2023， 230： 120552.

［11］Li Chunying， Guo Xiaojiao， Lin Weijie，et al. Multiplex network community detection algorithm based on motif awareness［J］. Know-ledge-Based Systems， 2023， 260： 110136.

［12］Liu Xingyu， Cheng Junwei， Cheng Hao，et al. Self-supervised community detection in multiplex networks with graph convolutional autoencoder ［C］// Proc of the 26th International Conference on Computer Supported Cooperative Work in Design. Piscataway，NJ：IEEE Press， 2023： 1378-1383.

［13］Magnani M， Hanteer O， Interdonato R，et al. Community detection in multiplex networks［J］. ACM Computing Surveys， 2021， 54（3）： 1-35.

［14］Pramanik S， Tackx R， Navelkar A，et al. Discovering community structure in multilayer networks ［C］// Proc of IEEE International Conference on Data Science and Advanced Analytics. Piscataway，NJ：IEEE Press， 2017： 611-620.

［15］Shao Minglai， Lin Yujie， Peng Qiyao，et al. Learning graph deep autoencoder for anomaly detection in multi-attributed networks［J］. Knowledge-Based Systems， 2023， 260： 110084.

［16］Newman M E J. Fast algorithm for detecting community structure in networks［J］. Physical Review E， 2004， 69（6）： 066133.

［17］He Chaobo， Zheng Yulong， Cheng Junwei，et al. Semi-supervised overlapping community detection in attributed graph with graph convolutional autoencoder［J］. Information Sciences， 2022， 608： 1464-1479.

［18］Bo Deyu， Wang Xiao， Shi Chuan，et al. Structural deep clustering network ［C］// Proc of Web Conference. New York： ACM Press， 2020： 1400-1410.

［19］Fan Shaohua， Wang Xiao， Shi Chuan，et al. One2multi graph autoencoder for multi-view graph clustering ［C］// Proc of Web Conference. New York： ACM Press， 2020： 3070-3076.

［20］Liu Weiyi， Chen P Y， Yeung S，et al. Principled multilayer network embedding ［C］// Proc of IEEE International Conference on Data Mining Workshops. Piscataway，NJ：IEEE Press， 2017： 134-141.

［21］Nie Feiping， Li Jing， Li Xuelong. Self-weighted multiview clustering with multiple graphs［C］//Proc of IJCAI. San Francisco： Morgan Kaufmann Publishers， 2017： 2564-2570.