強(qiáng)化學(xué)習(xí)下淺充淺放充電策略AGV調(diào)度研究

摘 要：針對(duì)自動(dòng)化集裝箱碼頭自動(dòng)導(dǎo)引車(chē)（AGV）調(diào)度中的充電問(wèn)題，考慮淺充淺放充電策略構(gòu)建了混合整數(shù)優(yōu)化模型。該模型以最小化AGV最終完工時(shí)間為目標(biāo)，在考慮AGV電池電量變化以及AGV不同狀態(tài)耗電差異的約束下，利用AGV空閑時(shí)間和一個(gè)作業(yè)循環(huán)結(jié)束時(shí)間補(bǔ)電，減少AGV充電次數(shù)，進(jìn)而減少總完成時(shí)間。模型采用Wolf-PHC強(qiáng)化學(xué)習(xí)進(jìn)行求解，并分別與GAMS求解器、Q-learning算法及遺傳算法（genetic algorithm，GA）求解結(jié)果進(jìn)行比較，以驗(yàn)證模型的有效性和算法的優(yōu)越性。算例分析表明在淺充淺放充電策略下AGV利用效率較高，且Wolf-PHC與GA的結(jié)合對(duì)模型求解效果更佳。

關(guān)鍵詞：自動(dòng)化集裝箱碼頭；自動(dòng)導(dǎo)引車(chē)；淺充淺放充電策略；強(qiáng)化學(xué)習(xí)；遺傳算法

中圖分類號(hào)：U691.3 文獻(xiàn)標(biāo)志碼：A 文章編號(hào)：1001-3695（2024）10-022-3038-06

doi：10.19734/j.issn.1001-3695.2024.03.0057

Research on AGV scheduling of shallow charging and shallow discharging charging strategy under reinforcement learning

Zhao Rui，Liang Chengji

（Institute of Logistics Science and Engineering，Shanghai Maritime University，Shanghai 201306，China）

Abstract：For charging problem in AGV scheduling in automated container terminals，this paper constructed a mixed integer optimization model considering the shallow charging and shallow discharging charging strategy.The model aimed to minimize the final completion time of the AGV.Under the constraints of considering the change of AGV battery power and the difference in power consumption in different states of the AGV，the model used the AGV idle time and the end time of a work cycle to make up power，reducing the number of AGV charging times，and thus reducing the total completion time.The model was solved by Wolf-PHC reinforcement learning，and the results were compared with GAMS solver，Q-learning algorithm and genetic algorithm（GA）respectively to verify the effectiveness of the model and superiority of the algorithm.The example analysis shows that AGV utilization efficiency is higher under the shallow charging and shallow discharging charging strategy，and the combination of Wolf-PHC and GA is better for the model solution.

Key words：automated container terminal;automatic guided vehicle（AGV）;shallow charge and shallow discharge charging strategy;reinforcement learning;genetic algorithm

0 引言

自動(dòng)化集裝箱碼頭始于20世紀(jì)90年代初，AGV是自動(dòng)化集裝箱碼頭的關(guān)鍵組成，承擔(dān)著水平運(yùn)輸任務(wù)。在實(shí)際作業(yè)中，AGV需要及時(shí)充電，否則將影響整個(gè)自動(dòng)化集裝箱碼頭正常作業(yè)。因此，在自動(dòng)化集裝箱碼頭運(yùn)行過(guò)程中AGV充電是一重要環(huán)節(jié)。為提高自動(dòng)化集裝箱碼頭AGV的作業(yè)效率，使AGV能安全可靠地投入到作業(yè)中，自動(dòng)化集裝箱碼頭AGV調(diào)度問(wèn)題成為了國(guó)內(nèi)外學(xué)者的研究熱點(diǎn)。Liu等人［1］基于海鐵聯(lián)運(yùn)集裝箱碼頭新建的U型堆場(chǎng)布局，重點(diǎn)研究了水平運(yùn)輸設(shè)備和裝卸設(shè)備的綜合調(diào)度，以及AGV的路徑規(guī)劃。Wang等人［2］研究了如何在正常生產(chǎn)和突發(fā)故障兩種情況下，以總成本最小化為目標(biāo)，將任務(wù)分配給多個(gè)AGV。李靜等人［3］設(shè)計(jì)了兩階段的算法，在考慮AGV負(fù)載以及沖突情況下，以最小化AGV能量消耗為目標(biāo)對(duì)模型進(jìn)行求解。梁承姬等人［4］采用多學(xué)科變量耦合優(yōu)化設(shè)計(jì)的方法對(duì)自動(dòng)化碼頭AGV調(diào)度與AGV配置問(wèn)題進(jìn)行研究，并設(shè)計(jì)遺傳算法、粒子群算法和蟻群算法分別進(jìn)行求解。王鼎新［5］將人工神經(jīng)網(wǎng)絡(luò)引入Q-learning算法使AGV可以通過(guò)自主學(xué)習(xí)進(jìn)行全局優(yōu)化。初良勇等人［6］提出一種基于DQN的可變調(diào)度策略的調(diào)度算法，以有效提升AGV利用率。上述文獻(xiàn)只是通過(guò)不同的模型和算法單獨(dú)對(duì)AGV調(diào)度進(jìn)行研究，沒(méi)有考慮到AGV為電力驅(qū)動(dòng)，存在電池續(xù)航與充電問(wèn)題，對(duì)AGV調(diào)度存在一定影響。

在生產(chǎn)實(shí)踐中發(fā)現(xiàn)AGV的充電過(guò)程一定程度上影響著自動(dòng)化集裝箱碼頭作業(yè)效率，AGV充電問(wèn)題引發(fā)部分學(xué)者的關(guān)注。Gao等人［7］考慮動(dòng)態(tài)環(huán)境對(duì)AGV運(yùn)行效率的影響，使用編程模型和Q-learning算法生成考慮電池充電的AGV調(diào)度計(jì)劃。Zhan等人［8］提出AGV雙極電池充電策略，制定了兩階段的啟發(fā)式算法，第一階段AGV根據(jù)最近充電站和最小延遲充電站選擇，第二階段考慮到鋰離子充電特性，減少了每次充電的持續(xù)時(shí)間。Nitish等人［9］針對(duì)AGV調(diào)度問(wèn)題，考慮AGV電量臨界值建立混合整數(shù)線性規(guī)劃模型，提出一種利用自適應(yīng)大領(lǐng)域搜索算法和線性程序求解的新數(shù)學(xué)方法。Nitish等人［10］討論了如何在電池有限的情況下對(duì)AGV進(jìn)行實(shí)時(shí)調(diào)度，以最大限度降低成本。趙濤等人［11］分析了AGV換電過(guò)程對(duì)調(diào)度的影響，考慮換電站數(shù)量和換電等待時(shí)間建立雙層耦合模型，以減少AGV換電時(shí)間，提升AGV利用率。石楠路等人［12］構(gòu)建了考慮換電過(guò)程的AGV作業(yè)調(diào)度混合整數(shù)優(yōu)化模型并通過(guò)遺傳算法求解。楊其飛等人［13］對(duì)AGV充電策略進(jìn)行優(yōu)劣性對(duì)比，通過(guò)遺傳算法對(duì)分析各充電策略對(duì)作業(yè)時(shí)間的影響，并得出應(yīng)用機(jī)會(huì)充電時(shí)最佳充電區(qū)間。吳洪明等人［14］考慮AGV電池電量約束，在機(jī)會(huì)充電模式的前提下研究AGV充電過(guò)程對(duì)作業(yè)效率的影響，進(jìn)而確定AGV最佳充電區(qū)間。Xie等人［15］提出一種以離線充電為主在線充電為輔的充電策略，并通過(guò)大量仿真實(shí)驗(yàn)證明該充電策略的有效性。Ma等人［16］提出了分散式、集中式兩種充電站布局及保守充電、漸進(jìn)充電兩種充電策略，并進(jìn)行了廣泛的仿真實(shí)驗(yàn)，分析了參數(shù)對(duì)系統(tǒng)性能的影響。誤偉民［17］以廈門(mén)自動(dòng)化碼頭為研究對(duì)象，研究得出充電站的布局、充電管理系統(tǒng)的開(kāi)發(fā)和實(shí)施對(duì)提高AGV充電過(guò)程的安全和效率有極大影響，并提出相關(guān)措施和建議。郄佩琦等人［18］為解決因充電樁布局不合理導(dǎo)致充電樁利用率低的問(wèn)題，考慮區(qū)域繁忙度，提出了AGV充電樁選址模型，從而有效提升系統(tǒng)整體效率。朱林等人［19］對(duì)AGV換電模式進(jìn)行創(chuàng)新，設(shè)計(jì)了AGV分布式淺充淺放循環(huán)充電系統(tǒng)，取消了換電環(huán)節(jié)，提高AGV利用率。唐立輝等人［20］針對(duì)我國(guó)投產(chǎn)應(yīng)用的三種AGV換電方式分別從建設(shè)成本、作業(yè)效率、安全性能及港口建設(shè)方面進(jìn)行了對(duì)比研究。

綜上所述，針對(duì)自動(dòng)化集裝箱碼頭AGV研究中，大部分文獻(xiàn)側(cè)重于AGV調(diào)度，忽略了AGV電量約束與充電對(duì)調(diào)度過(guò)程的影響。對(duì)于考慮AGV充電的文獻(xiàn)中，多數(shù)以換電池方式與機(jī)會(huì)充電方式為背景，且求解方法局限于單一的啟發(fā)式算法。本文結(jié)合自動(dòng)化碼頭AGV實(shí)際作業(yè)情況，針對(duì)自動(dòng)化碼頭淺充淺放充電策略，建立AGV調(diào)度模型，AGV通過(guò)空閑時(shí)間和每個(gè)作業(yè)循環(huán)與堆場(chǎng)交互時(shí)間補(bǔ)電，減少AGV因電量低于充電閾值去充電站的次數(shù)從而提高AGV作業(yè)效率。模型采用Wolf-PHC強(qiáng)化學(xué)習(xí)進(jìn)行求解，并分別與GAMS求解器和GA求解結(jié)果進(jìn)行比較，以驗(yàn)證模型的有效性和算法的優(yōu)越性。

1 問(wèn)題描述

1.1 自動(dòng)化碼頭AGV充電

自動(dòng)化集裝箱碼頭純電動(dòng)AGV的充電方式可分為換電池方式、樁式充電和非接觸式充電［17］。換電池方式要建設(shè)換電站并且配備一定數(shù)量的備用電池，不僅費(fèi)用昂貴還要占用碼頭專用場(chǎng)地。另外，AGV換電池方式采用滿充滿放式策略，嚴(yán)重縮短了電池壽命。且AGV換電池操作也占用了作用時(shí)間，若出現(xiàn)電池?cái)?shù)量不足或換電站故障則會(huì)導(dǎo)致碼頭停產(chǎn)。樁式充電只需要建設(shè)一定數(shù)量的充電樁，但AGV需要進(jìn)行較長(zhǎng)時(shí)間的充電，在作業(yè)高峰期導(dǎo)致AGV供應(yīng)不足，導(dǎo)致AGV利用效率大大降低。非接觸式充電可以在車(chē)輛行走路線上安裝非接觸式充電裝置，可實(shí)現(xiàn)車(chē)輛不需停車(chē)即可充電。淺充淺放充電策略不需要配備備用電池，而是利用非接觸式充電裝置，可利用AGV與堆場(chǎng)交互時(shí)間進(jìn)行不停車(chē)補(bǔ)電，且淺充淺放充電策略較滿充滿方式策略一定程度地延緩電池壽命的減少。綜上，淺充淺放充電策略解決了傳統(tǒng)AGV換電成本高、電池壽命短、具有一定風(fēng)險(xiǎn)隱患等問(wèn)題，并且可以實(shí)現(xiàn)生產(chǎn)與充電同步進(jìn)行，可達(dá)到提升AGV作業(yè)效率、有效提高自動(dòng)化碼頭整體作業(yè)效率、降低碼頭投資成本的目的。自動(dòng)化碼頭布局如圖1所示，主要分為泊位、AGV-岸橋交互區(qū)、AGV等待區(qū)、AGV-堆場(chǎng)交互區(qū)。

1.2 AGV淺充淺放充電策略

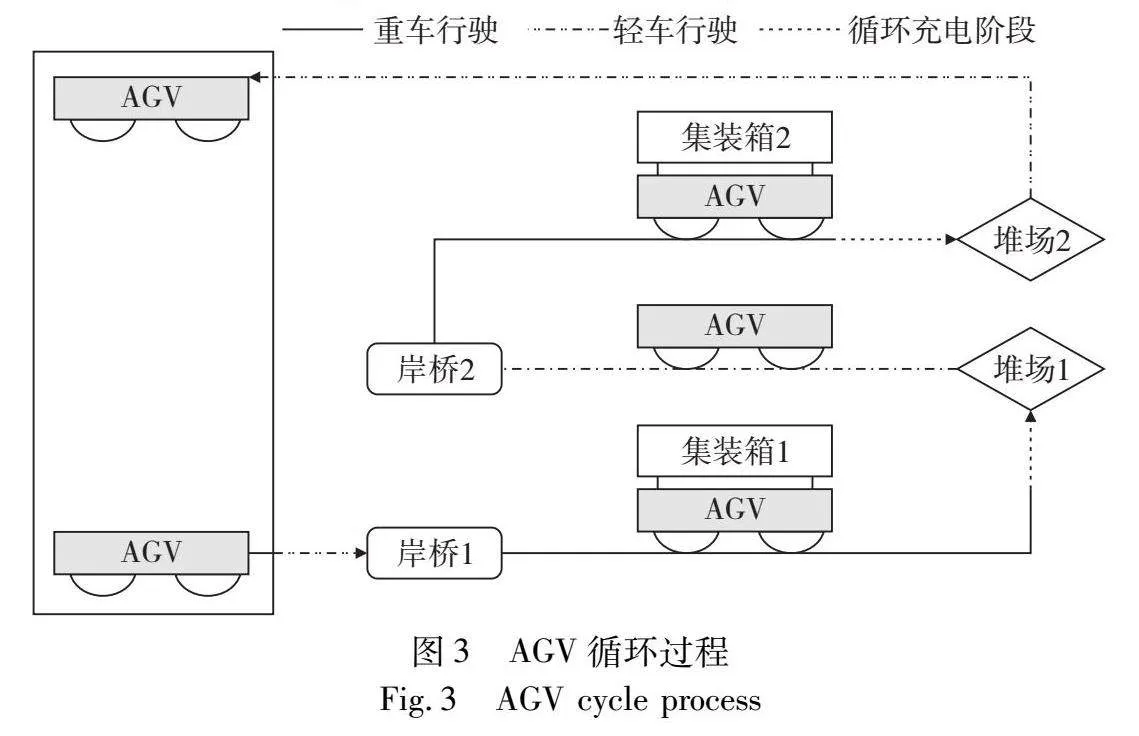
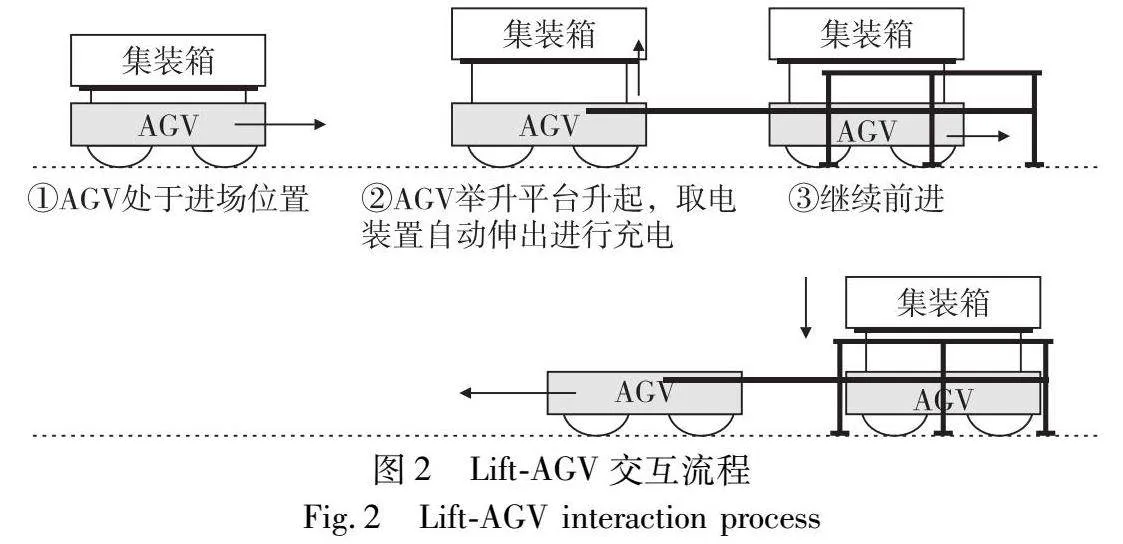
淺充淺放充電策略中，創(chuàng)新AGV交互流程，采用新型Lift-AGV［21］。Lift-AGV裝有舉升平臺(tái)如圖2所示，AGV作業(yè)循環(huán)末行駛至堆場(chǎng)交互區(qū)利用固定支架完成與軌道吊的交互，全程僅需要一分鐘同時(shí)進(jìn)行補(bǔ)電。當(dāng)AGV剩余極少電量時(shí)，行駛至充電樁進(jìn)行充電至滿電。但任務(wù)量大時(shí)AGV循環(huán)放電大于循環(huán)充電，易出現(xiàn)電量不足情況，而且AGV電量減少到一定程度一次補(bǔ)電至滿時(shí)間過(guò)長(zhǎng)，易造成AGV額外等待時(shí)間。本文針對(duì)上述狀況，考慮AGV有足夠的空閑時(shí)間到充電樁進(jìn)行補(bǔ)電的情況，減少AGV電量低于充電閾值補(bǔ)電的次數(shù)，充分發(fā)揮淺充淺放充電策略的優(yōu)勢(shì)，提高AGV作業(yè)效率。上文所提“空閑時(shí)間”也就是AGV等待所分配任務(wù)到達(dá)時(shí)間，若AGV空閑時(shí)間大于其從上一任務(wù)卸箱位置到充電樁的時(shí)間與充電樁到先任務(wù)接箱位置的時(shí)間之和，則稱AGV有“足夠的空閑時(shí)間”。如圖3所示為AGV循環(huán)過(guò)程。AGV從岸橋1運(yùn)輸任務(wù)1至堆場(chǎng)1，此過(guò)程經(jīng)歷循環(huán)充電階段。完成任務(wù)1后，判斷AGV剩余電量是否低于充電閾值和AGV是否有足夠空閑時(shí)間。若AGV剩余電量大于充電閾值且沒(méi)有足夠空閑時(shí)間，則AGV被指派到岸橋2將集裝箱任務(wù)2運(yùn)輸至堆場(chǎng)2。完成集裝箱任務(wù)2后再次進(jìn)行上述判斷，若AGV剩余電量低于充電閾值或有足夠空閑時(shí)間則去充電站充電，至此一個(gè)循環(huán)結(jié)束。由于AGV電量不同且空車(chē)行駛與重車(chē)行駛耗電率差異較大，需要區(qū)分考慮。

2 模型建立

2.1 模型假設(shè)

對(duì)所建AGV調(diào)度模型需作出如下假設(shè)：a）AGV初始電量均為100%；b）不考慮設(shè)備故障及碰撞；c）任務(wù)到達(dá)時(shí)間已知；d）不考慮岸橋操作時(shí)間；e）不考慮充電排隊(duì)等待時(shí)間。

2.2 符號(hào)說(shuō)明

本文所使用符號(hào)及說(shuō)明如表1、2所示。

2.3 AGV調(diào)度數(shù)學(xué)模型

式（1）為目標(biāo)函數(shù)，表示最小化AGV最大完工時(shí)間。

Min T（1）

式（2）為最終任務(wù)完成時(shí)間不小于任意任務(wù)的完成時(shí)間。

s.t. T≥Zki，k∈K;i∈V（2）

式（3）和（4）表示每臺(tái)AGV必須完成虛擬開(kāi)始任務(wù)與虛擬結(jié)束任務(wù)。

∑i∈V0xkij=1 j∈V;k∈K（3）

∑i∈V′0xkij=1 j∈V;k∈K（4）

式（5）和（6）表示每個(gè)任務(wù)僅有一個(gè)緊前和后續(xù)任務(wù)。

∑k∈K∑i∈Vtxkij=1 j∈V（5）

∑k∈K∑j∈Vtxkij=1 i∈V（6）

式（7）表示中間任務(wù)必須運(yùn)輸平衡，即輸入等于輸出。

∑i∈Vxkih-∑j∈Vxkhj=0 k∈K;h∈Vb∪Vt（7）

式（8）～（10）為等待時(shí)間，虛擬任務(wù)等待時(shí)間為0，換電任務(wù)的等待時(shí)間由完成上一任務(wù)剩余電量和充電樁充電速率決定，普通裝卸任務(wù)等待時(shí)間由到達(dá)發(fā)箱位置的時(shí)間和最早允許作業(yè)時(shí)間決定。

wki=0k∈K，i∈V0∪V0′WWkik∈K，i∈Vk（8）

WWki=（100-bbkj）/v3+（1-xjik）M k∈K，i∈Vk，j∈V（9）

wkj≥qej-zki-edkj/s1+（xkij-1）M k∈K;j∈Vt;i∈V（10）

式（11）（12）為普通裝卸任務(wù)與換電任務(wù)的完成時(shí)間。

zkj≥zki+（1-Ckj）wkj+（1-Ckj）edkj/s1+Ckjbdkj/s1+Ckjcdkj/s1+（1-Ckj）akj+fdkj/s2+（1-xkij）M k∈K;j∈Vt;i∈V（11）

zkj≥zki+wkj+bdkj/s4+cdkj/s4+fdkj/s2+wwkj+（1-xkij）Mk∈K;j∈Vk;i∈V（12）

式（13）為AGV有足夠空閑時(shí)間充電所用時(shí)間。

aki=wki-bdki/s1-cdki/s1 k∈K;i∈Vt（13）

式（14）分別為接受普通裝卸任務(wù)AGV剩余電量。

bkj≤bbki+M（1-xkij）+Ckj（akjs3-r1bdkj/s1）k∈K;i∈V;j∈Vt（14）

式（15）為接受換電任務(wù)時(shí)AGV剩余電量不大于充電閾值。

bkj≤MB k∈K;j∈Vb（15）

式（16）（17）為AGV完成正常裝卸任務(wù)與換電任務(wù)時(shí)的剩余電量，與式（14）共同描述了AGV利用充淺放充電策略在有足夠空閑時(shí)間補(bǔ)電前后的電量和利用與堆場(chǎng)交互的時(shí)間充電后的電量。

bbki=bki-r1edki/s1-r2fdi/s2+MA k∈K;i∈Vt（16）

bbki=100-r1cdki/s1-r2fdi/s2+MA k∈K;i∈Vb∪V0（17）

式（18）為一臺(tái)AGV充電次數(shù)之和不允許超多最多充電次數(shù)n。

∑i∈Vxkij≤n k∈K;j∈Vk（18）

式（19）（20）為變量的約束條件。

xkij∈{0，1}，cki∈{0，1} k∈K;i，j∈V（19）

zki>0，f>0，100≥bbki>0，wki≥0，edki≥0cdki≥0，bdki≥0 k∈K;i∈V（20）

3 基于Wolf-PHC的強(qiáng)化學(xué)習(xí)算法

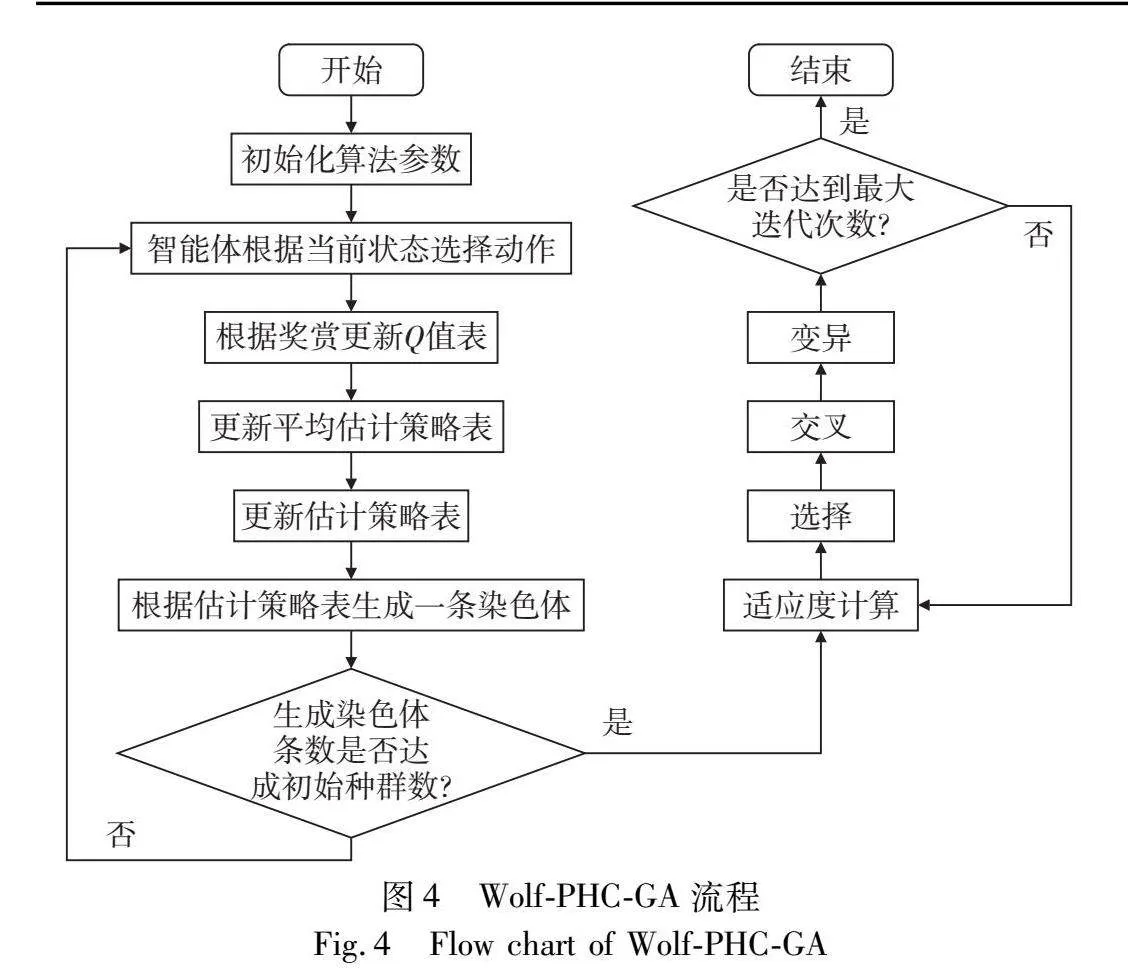
強(qiáng)化學(xué)習(xí)是一種運(yùn)用智能體與環(huán)境進(jìn)行“試錯(cuò)”交互，通過(guò)實(shí)時(shí)獎(jiǎng)懲值獲得反饋，尋找最大累計(jì)獎(jiǎng)賞值策略的機(jī)器學(xué)習(xí)方法［22］。Wolf-PHC是強(qiáng)化學(xué)習(xí)中的一種，是win or learn fast規(guī)則與policy hill-climbing算法的結(jié)合，Wolf指的是當(dāng)智能體獎(jiǎng)賞值較好時(shí)緩慢調(diào)參，反之加快調(diào)參，PHC算法的核心就是通常強(qiáng)化學(xué)習(xí)思想。強(qiáng)化學(xué)習(xí)中的很多方法都需要在學(xué)習(xí)過(guò)程中維護(hù)Q函數(shù)，Wolf-PHC每個(gè)智能體只用保存自己的動(dòng)作來(lái)完成學(xué)習(xí)任務(wù)較其他強(qiáng)化學(xué)習(xí)算法在需存儲(chǔ)空間方面有較大的優(yōu)勢(shì)。Wolf-PHC具有優(yōu)秀的自學(xué)習(xí)和優(yōu)化能力，可通過(guò)不斷試錯(cuò)和學(xué)習(xí)，找到AGV最優(yōu)的充電時(shí)機(jī)，使AGV在運(yùn)行過(guò)程中實(shí)現(xiàn)能源的高效利用和自主決策。具體而言，Wolf-PHC可以根據(jù)AGV的實(shí)時(shí)狀態(tài)、任務(wù)需求以及充電站距離等情況，動(dòng)態(tài)調(diào)整充電調(diào)度策略。例如，Wolf-PHC可以有效指導(dǎo)AGV利用空閑時(shí)間前往最近的充電樁補(bǔ)電；而當(dāng)AGV電量低于充電閾值時(shí)，Wolf-PHC則可以優(yōu)化其任務(wù)分配，指導(dǎo)AGV到充電樁進(jìn)行充電至滿。綜上可知Wolf-PHC與AGV充電調(diào)度模型具有較高的關(guān)聯(lián)度，該結(jié)合可以實(shí)現(xiàn)AGV充電過(guò)程的智能調(diào)度和優(yōu)化，進(jìn)而為自動(dòng)化集裝箱碼頭系統(tǒng)的高效運(yùn)行提供有力支持。因GA［23］在求解復(fù)雜優(yōu)化問(wèn)題中應(yīng)用廣泛，且有較好的魯棒性。本文將Wolf-PHC與GA進(jìn)行結(jié)合，利用Wolf-PHC生成初始種群帶入GA，具體流程如圖4所示。

本文將AGV定義為agent，定義動(dòng)作為集裝箱任務(wù)編號(hào)，狀態(tài)為不同電量區(qū)間AGV行駛的速度。agent之間通過(guò)競(jìng)爭(zhēng)選擇集裝箱任務(wù)后，合作共同尋找到使完成任務(wù)總時(shí)間最少的策略。淺充淺放循環(huán)充電策略中AGV會(huì)利用與堆場(chǎng)交互時(shí)進(jìn)行短時(shí)間的補(bǔ)電，因此設(shè)置AGV去充電樁補(bǔ)電的閾值會(huì)很低，也會(huì)導(dǎo)致AGV因低于閾值補(bǔ)電的時(shí)間會(huì)很長(zhǎng)。本文考慮淺充淺放循環(huán)充電策略的規(guī)則，根據(jù)最小化完成任務(wù)時(shí)間構(gòu)造獎(jiǎng)勵(lì)函數(shù)。但Wolf-PHC的目標(biāo)是累計(jì)獎(jiǎng)勵(lì)值最大化，因此獎(jiǎng)勵(lì)函數(shù)與完成任務(wù)所需時(shí)間呈負(fù)相關(guān)，用式（21）表示。

r（s，a）=-zki（21）

操作步驟如下：

a）輸入集裝箱任務(wù)屬性，充電樁-堆場(chǎng)-岸橋距離。初始化種群大小popsize，動(dòng)作選擇概率egreedy，探索迭代次數(shù)episode，狀態(tài)s出現(xiàn)次數(shù)C（s），策略效果較差學(xué)習(xí)率δl，策略效果較好學(xué)習(xí)率δw，Q值表，πk值表，πk值表。

πk（s，ak）=1/|Ak|，πk（s，ak）=1/|Ak| δl>δw（22）

b）智能體k根據(jù)當(dāng)前的狀態(tài)s采用ε-貪心策略得到動(dòng)作ac并執(zhí)行。

c）觀測(cè)下一個(gè)獎(jiǎng)賞值rk和下一個(gè)狀態(tài)s′更新Qk（s，ac），本文設(shè)置獎(jiǎng)賞值為AGV執(zhí)行集裝箱任務(wù)所用時(shí)間。

Qk（s，ac）=Qk（s，ac）+α［rk+γmaxQk（s′，a′）-Qk（s，ac）］（23）

d）對(duì)于每個(gè)ak∈Ak，更新平均估計(jì)策略πk（s，ak）。

C（s）=C（s）+1（24）

πk（s，ak）=πk（s，ak）+1/C（s）［πk（s，ak）-πk（s，ak）］（25）

e）根據(jù)Qk（s，ac），對(duì)每個(gè)ak∈Ak更新πk（s，ak）。

πk（s，ak）=πk（s，ak）+Δsa（26）

Δsak=-δsakak≠argmaxa′Q（s，a′）∑a′≠akδsakothers（27）

δsa=min（πk（s，ak），δ/|Ak|-1）（28）

δ=δw∑ak∈Akπk（s，ak）Qk（s，ak）>∑ak∈Akπk（s，ak）Qk（s，ak）δlothers（29）

f）根據(jù)πi值表選出每個(gè)任務(wù)完成時(shí)間最短的AGV得出染色體，染色體編碼如圖5所示。染色體長(zhǎng)度由任務(wù)數(shù)量決定，第i個(gè)位置的編碼k表示第i個(gè)任務(wù)由AGVk完成。

g）判斷是否達(dá)到初始種群數(shù)，如果是則輸出初始種群，否則執(zhí)行步驟b）。

h）輸入Wolf-PHC生成的初始種群，最大迭代次數(shù)generation，交叉概率Pc，變異概率Pm。

i）取調(diào)度模型目標(biāo)函數(shù)即在淺充淺放充電策略下最小化AGV最大完工時(shí)間的倒數(shù)作為適應(yīng)度函數(shù)值，1/T。

j）選擇，本文采用輪盤(pán)賭選擇方法。

k）交叉，本文采用兩點(diǎn)交叉法。

l）變異，本文交換變異方法。

m）判斷是否到最大迭代次數(shù)，如果是則結(jié)束迭代，否則執(zhí)行步驟i）。

4 算例分析

4.1 算例參數(shù)設(shè)置

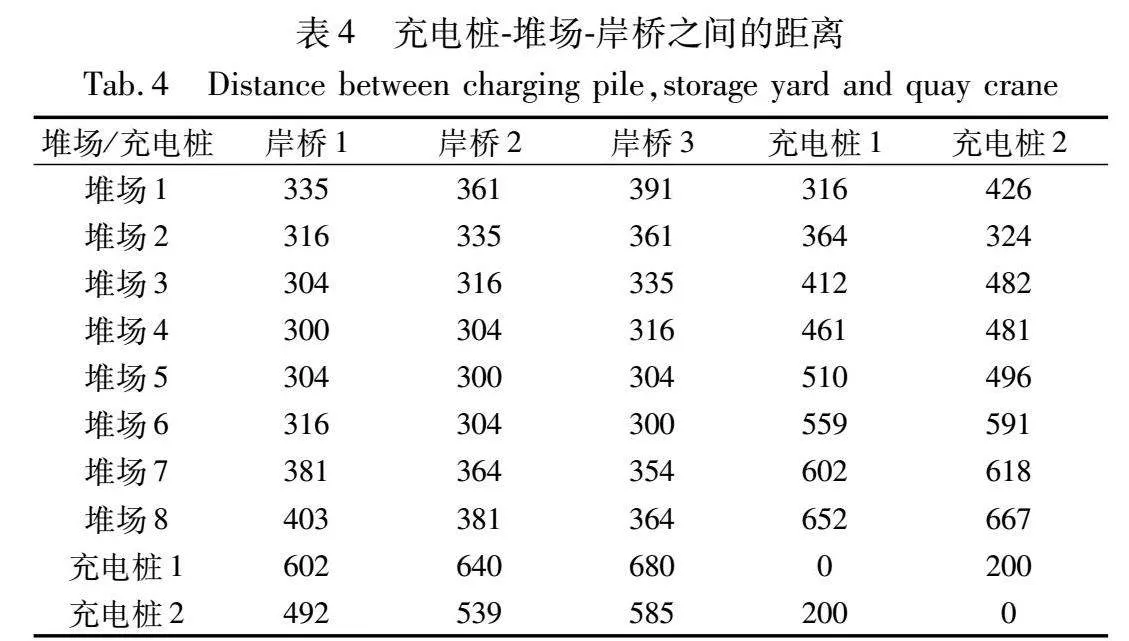
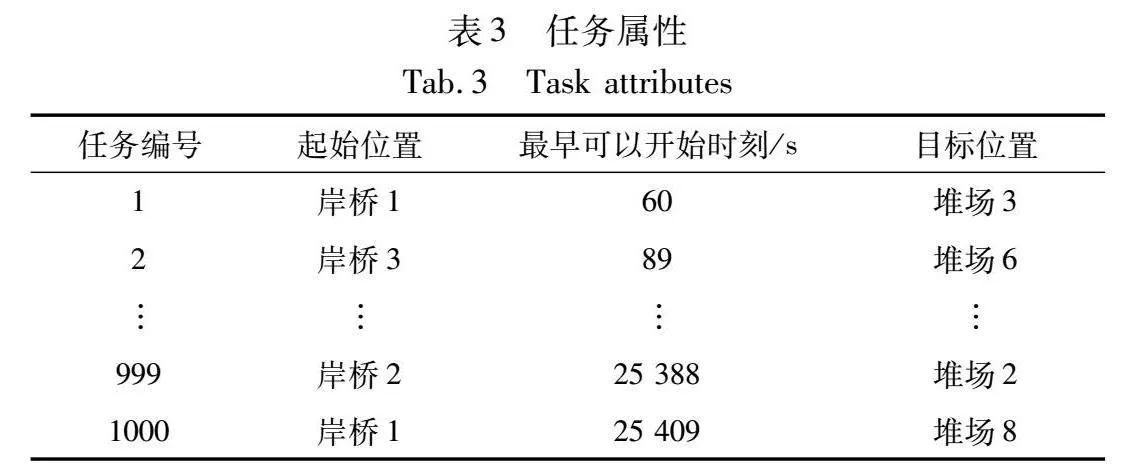
為評(píng)估所建立模型的準(zhǔn)確性，通過(guò)GAMS求解器［24］求解得出模型在具體環(huán)境下的精確解，并與Wolf-PHC-GA、強(qiáng)化學(xué)習(xí)算法中較有代表性的Q-leaning算法［25］及GA所求得最優(yōu)解進(jìn)行對(duì)比分析，以突出Wolf-PHC與GA結(jié)合的有效性及優(yōu)越性。其中Wolf-PHC-GA、GA、Q-learning均運(yùn)行10次取平均值作為最終結(jié)果。產(chǎn)生1 000個(gè)集裝箱任務(wù)樣本，其屬性如表3所示。設(shè)置初始種群大小popsize=200，動(dòng)作選擇概率egreedy=0.9，探索迭代次數(shù)episode=20，策略效果較差學(xué)習(xí)率δl=0.8，策略效果較好學(xué)習(xí)率δw=0.4，最大迭代次數(shù)generation=200，交叉概率Pc=0.7，變異概率Pm=0.05。充電樁-堆場(chǎng)-岸橋之間的距離如表4所示。令充電閾值（MB）為20%，AGV電量高于充電閾值時(shí)空車(chē)、重車(chē)行駛速度分別為4 m/s、3 m/s，AGV電量低于充電閾值時(shí)空車(chē)、重車(chē)行駛速度分別為2 m/s、1 m/s，AGV空車(chē)、重車(chē)行駛狀態(tài)下每米耗電率分別為0.01%、0.02%，設(shè)置兩個(gè)充電樁。

4.2 不同AGV數(shù)量下小規(guī)模任務(wù)結(jié)果分析

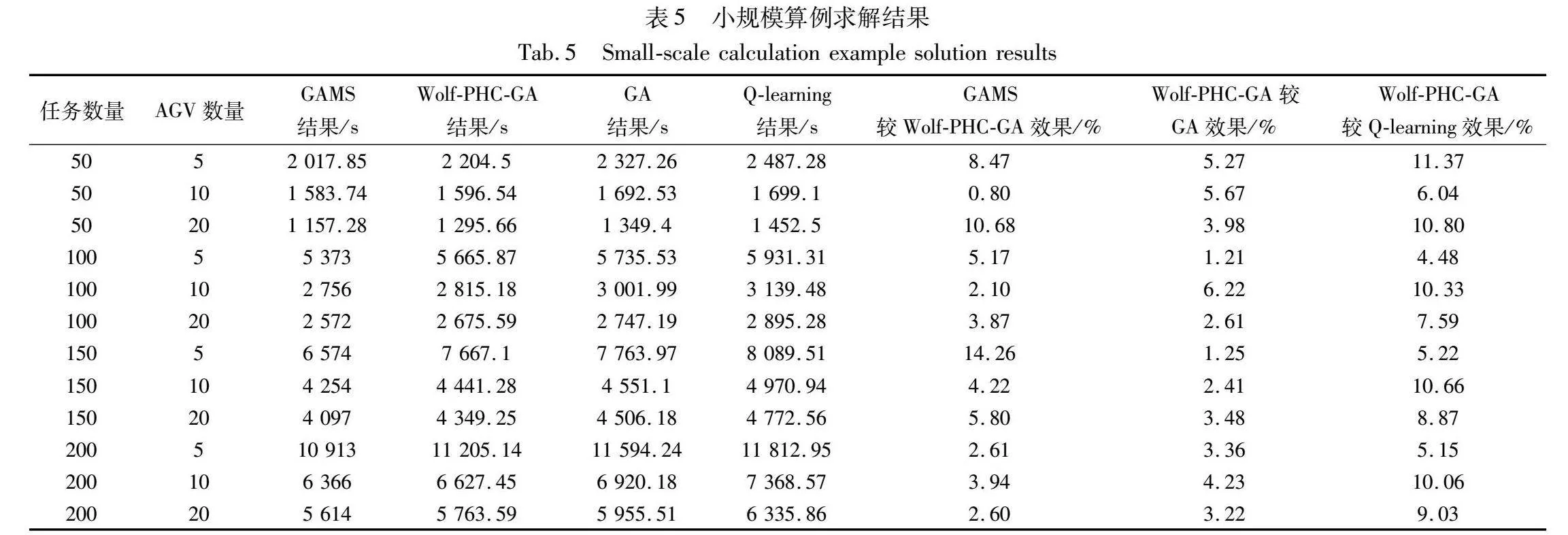
基于以上參數(shù)，求解小規(guī)模集裝箱任務(wù)規(guī)模及不同AGV數(shù)量的完工時(shí)間，如表5所示。從表5可以看出，小規(guī)模任務(wù)下Wolf-PHC-GA結(jié)果與GA結(jié)果的效果值多數(shù)在3%～8%，與Q-learning算法結(jié)果的效果值多數(shù)在5%～10%，而GAMS求得的精確解結(jié)果與Wolf-PHC-GA結(jié)果的效果值多數(shù)在8%以內(nèi)。有效說(shuō)明了Wolf-PHC-GA所求得最優(yōu)解不僅近似于精確解，還更優(yōu)于對(duì)比算法。

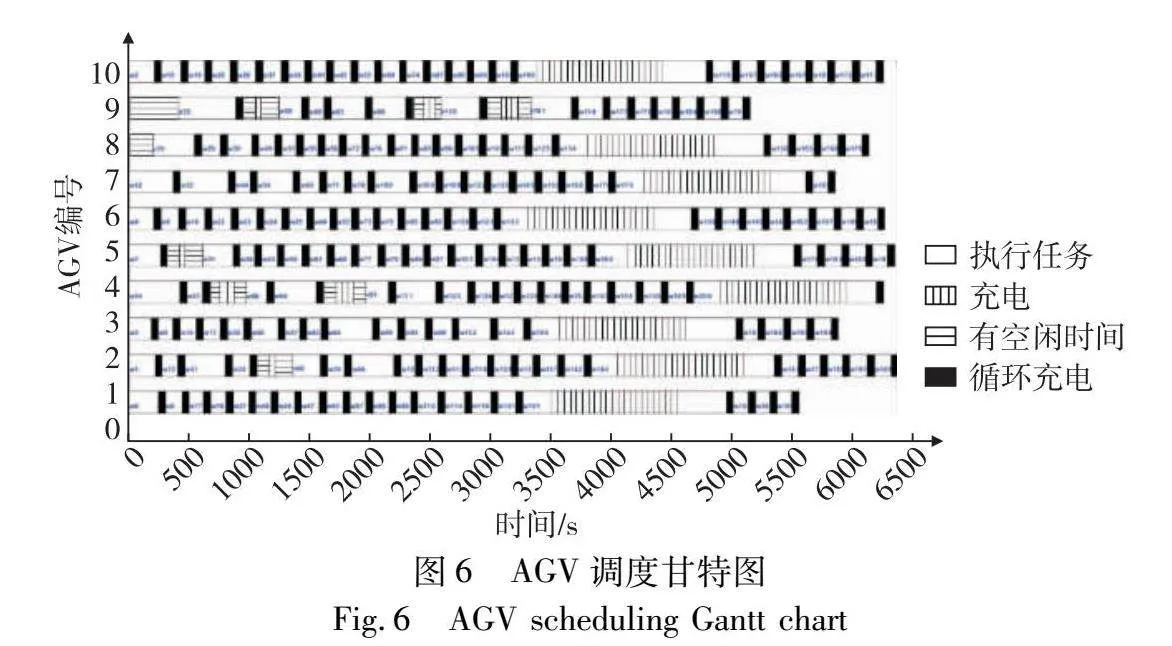
圖6為200個(gè)集裝箱任務(wù)10輛AGV調(diào)度甘特圖。可以看出，在淺充淺放充電策略下AGV可有效利用每個(gè)作業(yè)循環(huán)與堆場(chǎng)交互時(shí)間進(jìn)行補(bǔ)電與在AGV有足夠空閑時(shí)間進(jìn)行補(bǔ)電，很大程度上減少了AGV在充電樁補(bǔ)電的次數(shù)，從而減少作業(yè)時(shí)間。

4.3 不同AGV數(shù)量下大規(guī)模任務(wù)結(jié)果分析

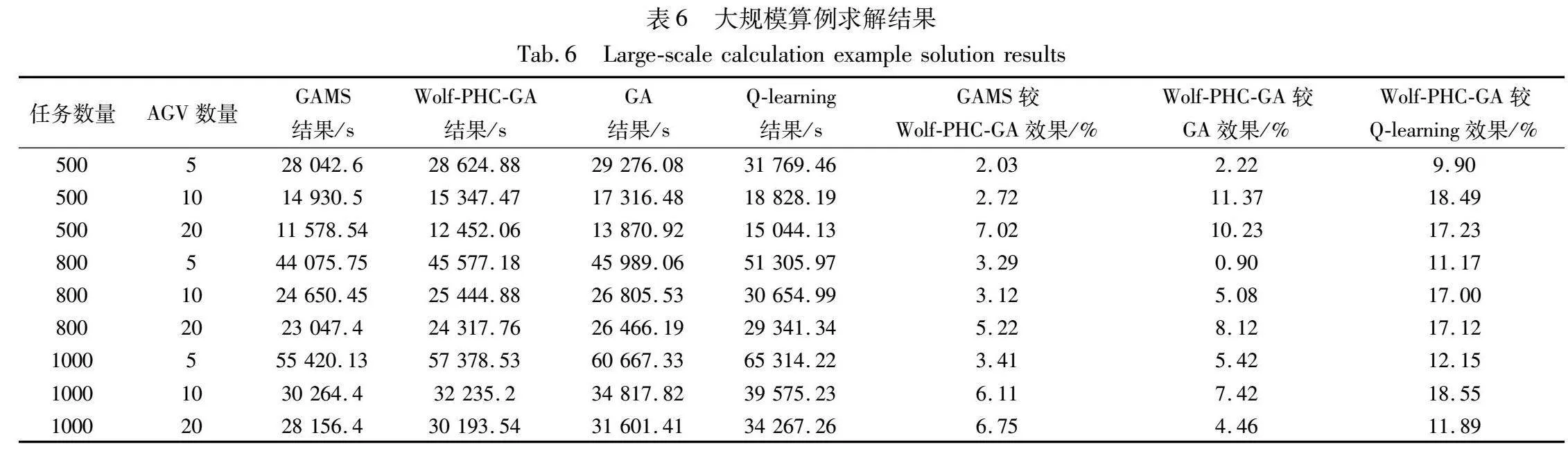
大規(guī)模集裝箱任務(wù)下，不同AGV數(shù)量的結(jié)果對(duì)比如表6所示。總體來(lái)看，大規(guī)模任務(wù)量?jī)?yōu)化效果比小規(guī)模任務(wù)量略勝一籌：Wolf-PHC-GA與GA的效果值多數(shù)在5%～10%，與Q-learning算法的效果值多數(shù)在10%～17%，而GAMS與Wolf-PHC-GA的效果值多數(shù)在6%以內(nèi)。說(shuō)明Wolf-PHC-GA求解大規(guī)模任務(wù)效果更佳，更適用于自動(dòng)化集裝箱碼頭實(shí)際運(yùn)作場(chǎng)景。

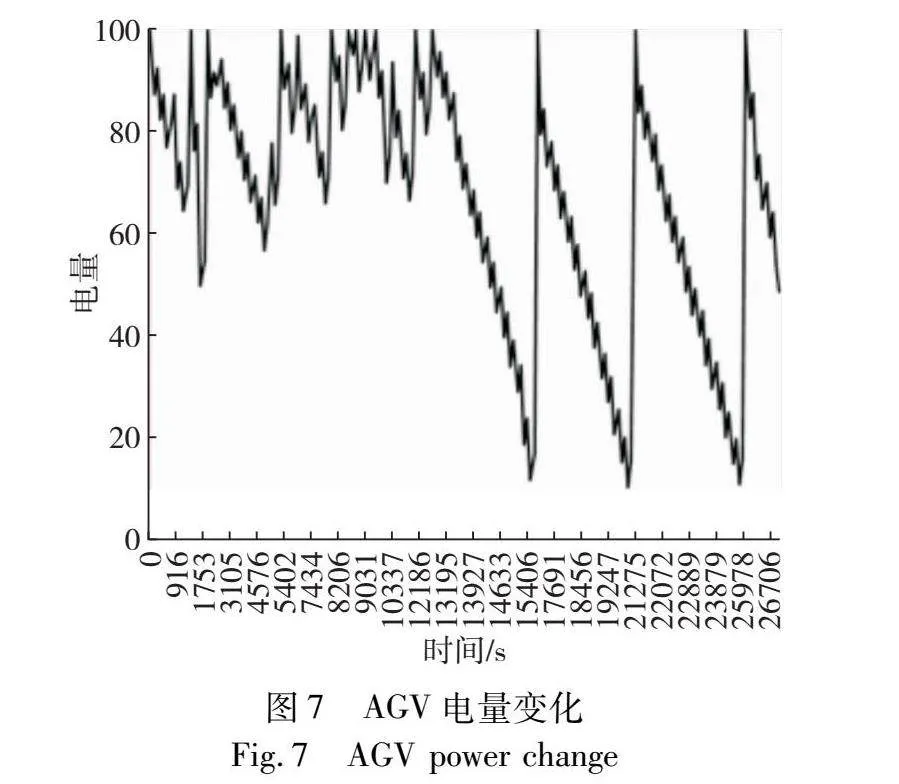
圖7為1 000個(gè)集裝箱任務(wù)10輛AGV調(diào)度中的一輛AGV電量變化。圖中均勻鋸齒狀下降部分反映了AGV與堆場(chǎng)交互時(shí)一分鐘補(bǔ)電的情況；在均勻鋸齒狀下降過(guò)程中會(huì)有上升的情況，代表AGV有足夠空閑時(shí)間補(bǔ)電；最后出現(xiàn)三次急劇上升的情況，則代表AGV因電量低于MB到充電樁進(jìn)行充電至滿。

4.4 充電閾值（MB）對(duì)結(jié)果影響分析

經(jīng)過(guò)上述對(duì)比分析可知MB對(duì)最終完工時(shí)間有較大影響，因此設(shè)定MB在13%～30%取值，分別取大小規(guī)模任務(wù)量10輛AGV進(jìn)行分析，最終得到的不同MB值對(duì)應(yīng)的完工時(shí)間如表7所示，AGV有足夠空閑時(shí)間補(bǔ)電及低于MB值充電次數(shù)如圖8所示。可以看出，改變MB值能夠影響AGV最終完工時(shí)間：當(dāng)MB值增大，AGV電量低于MB值充電次數(shù)程上升趨勢(shì)，小規(guī)模任務(wù)量利用空閑時(shí)間充電次數(shù)浮動(dòng)在5次以內(nèi)，大規(guī)模任務(wù)量效果更明顯，利用空閑時(shí)間充電次數(shù)整體呈下降趨勢(shì)。當(dāng)MB值在17%～20%取值時(shí)，完工時(shí)間較短。因此可見(jiàn)，合理設(shè)置MB值，更能發(fā)揮淺充淺放充電策略的優(yōu)勢(shì)。

4.5 不同學(xué)習(xí)率比值（δl/δw）對(duì)結(jié)果的影響分析

上述結(jié)果是在δl=0.8、δw=0.4時(shí)計(jì)算得出的。改變?chǔ)膌、δw的比值得到如表8所示的結(jié)果。從表中可看出，大小規(guī)模任務(wù)量在不同學(xué)習(xí)率比的影響下，完工時(shí)間變化在0.1～0.3 h。其中δl/δw=3時(shí)總完工時(shí)間最短，效果最好。

5 結(jié)束語(yǔ)

本文在自動(dòng)化集裝箱碼頭AGV調(diào)度過(guò)程中考慮了AGV淺充淺放充電策略，區(qū)分不同狀態(tài)下AGV耗電程度，考慮了充電過(guò)程對(duì)AGV作業(yè)效率的影響，建立了AGV調(diào)度混合整數(shù)優(yōu)化模型，運(yùn)用GAMS求解器驗(yàn)證所建立模型的有效性，并與Wolf-PHC-GA、GA、Q-learning算法進(jìn)行對(duì)比求解。在小規(guī)模算例下對(duì)比分析得出Wolf-PHC-GA求解結(jié)果比GA求解結(jié)果提升了3%～8%，比Q-learning求解結(jié)果提升了5%～10%，說(shuō)明了Wolf-PHC-GA求解的優(yōu)越性，并以200個(gè)任務(wù)10輛AGV為例說(shuō)明了淺充淺放充電策略可有效減少AGV低于閾值充電的次數(shù)，提高AGV利用率。大規(guī)模算例下Wolf-PHC-GA求解結(jié)果較GA求解結(jié)果提升5%～10%，較Q-learning求解結(jié)果提升10%～17%，進(jìn)一步說(shuō)明Wolf-PHC-GA求解的優(yōu)越性，并以1 000個(gè)任務(wù)10輛AGV為例分析AGV在淺充淺放充電策略下電量變化。通過(guò)對(duì)充電閾值的分析可知，設(shè)置充電閾值在17%～20%完工時(shí)間較短，有效提升自動(dòng)化碼頭工作效率。最后，對(duì)Wolf-PHC-GA中重要參數(shù)學(xué)習(xí)率比值進(jìn)行分析可得，在學(xué)習(xí)率比值為3時(shí)效果最佳。本文所建立混合整數(shù)優(yōu)化模型對(duì)于自動(dòng)化集裝箱碼頭AGV淺充淺放充電問(wèn)題具有一定指導(dǎo)意義。但是本文未考慮頻繁充放電對(duì)AGV電池壽命影響，可加深對(duì)此方面的研究。同時(shí)，可以繼續(xù)深入研究不同自動(dòng)化集裝箱碼頭布局、充電樁位置及數(shù)量與AGV淺充淺放充電的關(guān)系。

參考文獻(xiàn)：

［1］Liu Wenqian，Zhu Xiaoning，Wang Li，et al.Multiple equipment scheduling and AGV trajectory generation in U-shaped sea-rail intermodal automated container terminal［J］.Measurement，2023，206：112262.

［2］Wang Xue，Zou Wenqiang，Meng Leilei，et al.Effective metaheuristic and reschedul-eng strategies for the multi-AGV scheduling problem with sudden failure［J］.Expert Systems with Applications，2024，250：123473.

［3］李靜，朱小林.集裝箱碼頭上多自動(dòng)引導(dǎo)車(chē)的調(diào)度和路徑規(guī)劃［J］.計(jì)算機(jī)集成制造系統(tǒng)，2022，28（5）：1449-1461.（Li Jing，Zhu Xiaolin.Scheduling and path planning of multiple automatic guided vehicles in container terminals［J］.Computer Integrated Manufacturing Systems，2022，28（5）：1449-1461.）

［4］梁承姬，陳登川.自動(dòng)化集裝箱碼頭AGV配置與調(diào)度耦合問(wèn)題研究［J］.計(jì)算機(jī)工程與應(yīng)用，2020，56（14）：216-225.（Liang Chengji，Chen Dengchuan.Research on coupling problem of AGV configuration and scheduling in automated container terminal［J］.Computer Engineering and Applications，2020，56（14）：216-225.）

［5］王鼎新.基于改進(jìn)Q-learning算法的AGV路徑規(guī)劃［J］.電子設(shè)計(jì)工程，2021（4）：7-11.（Wang Dingxin.AGV path planning based on improved Q-learning algorithm［J］.Electronic Design Enginee-ring，2021（4）：7-11.）

［6］初良勇，梁冬.基于DQN的自動(dòng)化集裝箱碼頭AGV多目標(biāo)調(diào)度優(yōu)化［J］.哈爾濱工程大學(xué)學(xué)報(bào)，2024（5）：1-9.（Chu Liangyong，Liang Dong.Multi-objective scheduling optimization of AGVs in automated container terminal based on DQN［J］.Journal of Harbin Engineering University，2024（5）：1-9.）

［7］Gao Yinping，Chang Daofang，Chen C H，et al.A digital twin-based decision support approach for AGV scheduling［J］.Engineering Applications of Artificial Intelligence，2024，130：107687.

［8］Zhan Xiangnan，Xu Liyun，Zhang Jian，et al.Study on AGVs battery charging strategy for improving utilization［J］.Procedia CIRP，2019，81（3）：558-563.

［9］Nitish S，Quang-Vinh D，Alp A，et al.A matheuristic for AGV scheduling with battery constraints［J］.European Journal of Operational Research，2022，298（3）：855-873.

［10］Nitish S，Alp A，Quang-Vinh D，et al.Dispatching AGVs with battery constraints using deep reinforcement learning［J］.Computers & Industrial Engineering，2024，187：109678.

［11］趙濤，梁承姬，胡筱淵，等.自動(dòng)化集裝箱碼頭AGV調(diào)度與換電雙層模型求解［J］.大連理工大學(xué)學(xué)報(bào)，2021，61（6）：623-633.（Zhao Tao，Liang Chengji，Hu Xiaoyuan，et al.Solution of AGV scheduling and battery exchange two-layer model for automated container terminal［J］.Journal of Dalian University of Technology，2021，61（6）：623-633.）

［12］石楠路，梁承姬.考慮換電過(guò)程的自動(dòng)化碼頭AGV調(diào)度優(yōu)化［J］.現(xiàn)在制造工程，2019（2）：6-11.（Shi Nanlu，Liang Chengji.Optimization of AGV operation scheduling for automated terminal considering replacement processes［J］.Modern Manufacturing Engineering，2019（2）：6-11.）

［13］楊其飛，蘭培真.考慮充電過(guò)程的自動(dòng)化碼頭AGV調(diào)度［J］.集美大學(xué)學(xué)報(bào)：自然科學(xué)版，2023，28（2）：142-149.（Yang Qifei，Lan Peizhen.Automated terminal AGV scheduling considering the charging process［J］.Journal of Jimei University：Natural Science，2023，28（2）：142-149.）

［14］吳洪明，鄒夢(mèng)艷.考慮電池電量約束的自動(dòng)化碼頭AGV調(diào)度［J］.起重運(yùn)輸機(jī)械，2021（3）：47-52.（Wu Hongming，Zhou Mengyan.Automated terminal AGV scheduling considering battery power constraints［J］.Hoisting and Conveying Machinery，2021（3）：47-52.）

［15］Xie Danlan，Guo Di，Ji Yuan，et al.Simulation research on optimization of AGV charging strategy for automated terminal［J］.Journal of System Simulation，2020，32（10）：2227-2236.

［16］Ma Ning，Zhou Chenhao，Stephen A.Simulation model and perfor-mance evaluation of battery-powered AGV systems in automated container terminals［J］.Simulation Modelling Practice and Theory，2021，106：102146.

［17］吳偉民.廈門(mén)遠(yuǎn)海自動(dòng)化碼頭的充電裝置升級(jí)改造［J］.電子元器件與信息技術(shù)，2023，7（12）：209-212.（Wu Weimin.Charging device upgrade at Xiamen Yuan Hai automated terminal［J］.Electronic Components and Information Technology，2023，7（12）：209-212.）

［18］郄佩琦，陳傳軍，陳佳梁，等.基于區(qū)域繁忙度的AGV充電樁選址研究［J］.制造業(yè)自動(dòng)化，2023，45（8）：214-220.（Qie Peiqi，Chen Chuanjun，Chen Jialiang，et al.Research on AGV charging pile siting based on regional busyness［J］.Manufacturing Automation，2023，45（8）：214-220.）

［19］朱林，王偉，唐立輝，等.自動(dòng)化集裝箱碼頭AGV分布式淺充淺放循環(huán)充電系統(tǒng)［J］.港口裝卸，2020（6）：8-13.（Zhu Lin，Wang Wei，Tang Lihui，et al.AGV distributed shallow charging shallow discharge cycle charging system in automated container terminal［J］.Port Operation，2020（6）：8-13.）

［20］唐立輝，張連鋼.自動(dòng)化集裝箱碼頭水平運(yùn)輸系統(tǒng)動(dòng)力系統(tǒng)及充電方案［J］.水運(yùn)工程，2020（6）：74-78.（Tang Lihui，Zhang Liangang.Power system and charging scheme of horizontal transportation system of automated container system［J］.Port & Waterway Engineering，2020（6）：74-78.）

［21］王偉，孫秀良，徐哲，等.一種自動(dòng)化集裝箱碼頭純電動(dòng)AGV充電方式［J］.港口裝卸，2019，245（2）：1-2.（Wang Wei，Sun Xiuliang，Xu Zhe，et al.Charging mode of pure electric AGV in automated container terminal［J］.Port Operation，2019，245（2）：1-2.）

［22］傅啟明.強(qiáng)化學(xué)習(xí)中離策略算法的分析及研究［D］.蘇州：蘇州大學(xué)，2014.（Fu Qiming.Analysis and research on off-policy algorithms in reinforcement learning［D］.Suzhou：Suzhou University，2014.）

［23］許彭錦，梁承姬.考慮電池包數(shù)量的自動(dòng)化集裝箱碼頭多AGV調(diào)度優(yōu)化［J］.計(jì)算機(jī)應(yīng)用研究，2022，39（9）：2653-2659.（Xu Pengjin，Liang Chengji.Research on multi-AGV scheduling optimization of automated container terminal considering number of battery packs［J］.Application Research of Computers，2022，39（9）：2653-2659.）

［24］馬書(shū)艷.GAMS在復(fù)雜系統(tǒng)中的應(yīng)用研究［J］.科學(xué)技術(shù)創(chuàng)新，2020（31）：96-97.（Ma Shuyan.Research on the application of GAMS in complex systems［J］.Scientific and Technological Innovation，2020（31）：96-97.）

［25］趙德京，馬洪聰，王家曜，等.改進(jìn)Q學(xué)習(xí)算法在多智能體強(qiáng)化學(xué)習(xí)中的應(yīng)用［J］.自動(dòng)化與儀器儀表，2022（6）：13-16，22.（Zhao Dejing，Ma Hongcong，Wang Jiayao，et al.Application of improved Q learning algorithm to multi-intelligent body reinforcement learning［J］.Automation & Instrumentation，2022（6）：13-16，22.）