應用投影法求解n次方反比場場強的可行性討論


摘"要:投影法是一種等效求解電場強度的簡捷算法。本文嘗試應用投影法對n次方反比場中的場源在半圓形分布、無限長直線分布、半球面分布與無限大平面分布下的場強計算展開討論,得到了更具普遍意義的結論。
關鍵詞:投影法;n次方反比場;場源分布;場強;思想方法
1"問題緣起
陳澤南與陳輝老師的《投影法求解電場強度在競賽中的應用》(以下簡稱《投文》)一文中提出了投影法,即將某一帶電體上特定分布的電荷在某處產生電場與向某個方向投影后另一種分布的電荷產生電場等效來求解電場強度的方法。[1]運用該方法對場源電荷在半圓形分布、無限長直線分布、半球面分布與無限大平面分布這四種特殊分布下的電場強度進行了簡捷計算,避免了復雜的微積分運算。場源電荷在四種特殊分布下的電場強度如表1所示。
電場是一種二次方反比場,即場強大小與其到場源點的距離平方成反比。那么,投影法是否適用于任意的n次方反比場呢?本文將用投影法對n次方反比場中的場源在上述四種分布下的場強計算展開討論。
2"問題討論
為方便討論,筆者將n次方反比場的場源記為Q,為靜止點源;并認為該場源所產生的場強方向與正電荷類似,即從場源出發沿徑向指向無窮遠處。場強符號為E,且E=KQrn,其中K為比例系數。
2.1"半圓形分布
如圖1所示,場源呈半圓形均勻分布,線密度為η,半徑為r。在圓弧上取一弧元rΔθ,其所帶場源為ηrΔθ,該弧元對應的半徑與豎直方向成θ角。該弧元在圓心O點產生的場強Ei=KηrΔθrn,由對稱性可知該半圓弧在O點處產生的場強為
EO=Eicosθ=KηrnrΔθcosθ,
其中的rΔθcosθ可以看成弧元在直徑上的投影,則rΔθcosθ=2r。
因此,EO=2Kηrrn=2Kηrn-1,方向沿O′O方向。呈半圓形分布的場源在圓心處產生的場強可以等效成沿半圓弧直徑分布的場源η·2r集中于位置O′時在圓心O處產生的場強,這個沿半圓弧直徑分布的場源是原場源在垂直對稱軸方向上的投影,這一結論適用于任意的n次方反比場。
2.2"無限長直線分布
如圖2所示,場源沿無限長直線均勻分布,線密度為η,場點O到直線的垂直距離為r。在直線上取一線元,其長為Δl0,所帶場源為ηΔl0,該線元與O點的連線與豎直方向成θ角。由幾何關系知Δl1=Δl0cosθ,Δθ=Δl2r=Δl1rcosθ,可得Δl0=rΔθcos2θ,該線元在O點產生的場強為Ei=KηΔl0rcosθn=KηrΔθrcosθncos2θ=KηrΔθcosn-2θrn,由對稱性可知場源在O點的合場強EO=Eicosθ=KηrnrΔθcosn-1θ。對n取不同值的情況討論如下。
討論1:n=1,EO=KηrrΔθ=KηΔθ,考慮到場源沿無限長直線均勻分布,則有Δθ=π,則EO=Kηπ,方向沿O′O方向。n=1時,無限長直線分布場源在O點的場強可以等效成半徑為r的半圓弧所具有的場源ηπr集中于對稱軸上離點O為r的位置O′時在圓心O處產生的場強。這個沿半圓弧的場源是原場源向O點的投影。
討論2:n=2,EO=Kηr2rΔθcosθ,其中rΔθcosθ=Δl2cosθ=Δl3,可知,有Δl3=2r,則EO=2Kηr,這與《投文》中結果相符。
討論3:n≥3,EO=KηrnrΔθcosn-1θ=KηrnΔl3cosn-2θ,顯然此時式中Δl3cosn-2θ一項已不能再通過投影法進行簡捷計算,即此時利用投影法已不能簡化求解無限長直線形分布場源的場強。
2.3"半球面分布
如圖3所示,場源呈半球面均勻分布,面密度為σ,半球面半徑為r。在半球面上取一面元,其面積為ΔS,所帶場源為σΔS,該面元與O的連線與豎直方向成θ角。該面元在O點產生的場強為Ei=KσΔSrn,由對稱性可知場源在O點產生的場強EO=Eicosθ=KσΔSrncosθ=KσrnΔScosθ,
其中ΔScosθ可以看成面元ΔS在截面上的投影ΔS′。
因此EO=KσrnΔS′=Kσπr2rn=Kσπrn-2,方向沿O′O方向。半球面上均勻分布的場源在圓心產生的場強等效成圓面所具有的場源σπr2集中于對稱軸上位置O′時在圓心O處產生的場強,這個沿圓面分布的場源是原場源在半球截面上的投影,這一結論適用于任意的n次方反比場。
2.4"無限大平面分布
如圖4所示,場源呈無限大平面均勻分布,面密度為σ。在平面上取一面元ΔS0,所帶場源為σΔS0,其中ΔS1是ΔS0在與O點連線垂直方向的投影,ΔS2是半徑為r的半球面和ΔS1與O點所構成的圓錐體相交的面元,ΔS3是ΔS2在半球形上底面的投影。該面元ΔS0與O點的連線與豎直方向成θ角。該面元Δd0在O點產生的場強為Ei=KσΔS0dn,又d=rcosθ,Ei=KσcosnθrnΔS0,由對稱性可得無窮大平面上均勻分布的場源在O點產生的場強EO=Eicosθ=KσrnΔS0cosn+1θ。現對n取不同值的情況討論如下。
討論1:n=1,EO=KσrΔS0cos2θ,易知ΔS1=ΔS0cosθ。因此,EO=KσrΔS1cosθ,其中ΔS1cosθ一項無可供簡化計算的幾何意義,即無法通過投影法簡化計算此時的場強。
討論2:n=2,EO=Kσr2ΔS0cos3θ,由幾何關系知ΔS1=ΔS0cosθ,ΔS2r2=ΔS1d2,則ΔS2=ΔS1r2d2=ΔS1cos2θ,則ΔS2=ΔS0cos3θ。因此,EO=Kσr2ΔS2=2Kσπr2r2=2Kσπ,方向沿O′O方向。n=2時,呈無限大平面分布的場源在O點的場強,可以等效成沿半徑為r的半球面分布的場源2σπr2集中在對稱軸上離O點距離為r的位置O′時在圓心O處產生的場強。這個沿半球面分布的場源是原場源向O點的投影。
討論3:n=3,EO=Kσr3ΔS0cos4θ,由上可知ΔS2=ΔS0cos3θ,又有ΔS3=ΔS2cosθ,則ΔS3=ΔS0cos4θ。因此,EO=Kσr3ΔS3=Kσπr2r3=Kσπr,方向沿O′O方向。n=3時,呈無限大平面分布的場源在O點的場強,可以等效成沿半徑為r的圓面分布的場源σπr2集中在對稱軸上離O點距離為r的位置O′時在O點處產生的場強。這個沿圓面分布的場源是原場源先向O點投影成的半徑為r的半球面場源,再向底面投影式的。
討論4:n≥4,由討論3得EO=KσrnΔS3cosn-3θ,顯然此時式中的ΔS3cosn-3θ一項已經無法再通過投影法進行簡捷計算,即此時投影法已不能簡化求解呈無限大平面分布的場源的場強。
3"結語
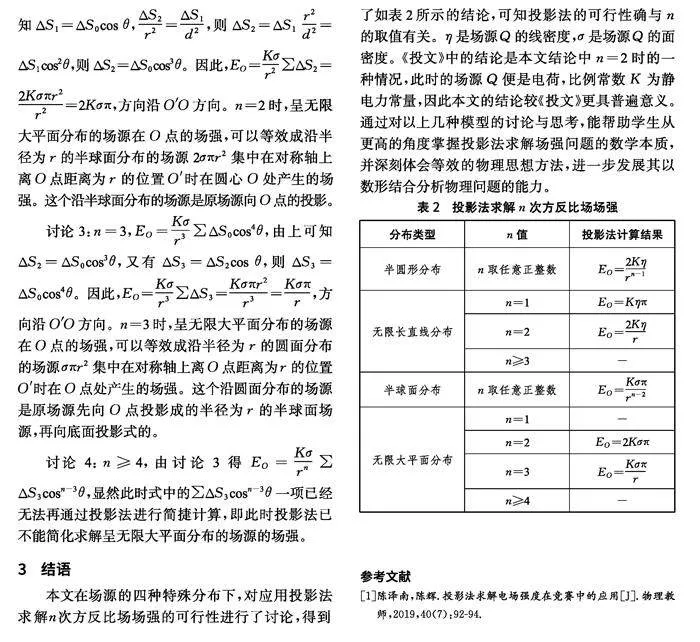
本文在場源的四種特殊分布下,對應用投影法求解n次方反比場場強的可行性進行了討論,得到了如表2所示的結論,可知投影法的可行性確與n的取值有關。η是場源Q的線密度,σ是場源Q的面密度。《投文》中的結論是本文結論中n=2時的一種情況,此時的場源Q便是電荷,比例常數K為靜電力常量,因此本文的結論較《投文》更具普遍意義。通過對以上幾種模型的討論與思考,能幫助學生從更高的角度掌握投影法求解場強問題的數學本質,并深刻體會等效的物理思想方法,進一步發展其以數形結合分析物理問題的能力。
參考文獻
[1]陳澤南,陳輝.投影法求解電場強度在競賽中的應用[J].物理教師,2019,40(7):92"-94.

