基于Keccak置換的認證加密算法改進與安全性評估

關鍵詞：Keccak置換；認證加密；算法改進；安全性評估

中圖分類號：TP308 文獻標識碼：A

文章編號：1009-3044（2024）26-0074-03 開放科學（資源服務）標識碼（OSID） ：

0 引言

Keccak置換是一種重要的密碼學原語，廣泛應用于哈希函數、消息認證碼和認證加密等領域。然而，現有的基于Keccak置換的認證加密算法在執行效率和并行性方面存在不足，難以滿足高吞吐量應用場景的需求。此外，面對日益增長的非對稱威脅，現有算法的安全機制需要進一步增強，因此需要進行深入研究以改進算法效果。

1 Keccak 置換的基本原理

Keccak置換基于海綿結構，是一種重要的密碼學原語，被廣泛應用于哈希函數、消息認證碼以及認證加密等領域。其核心是通過一系列的置換操作，將輸入的比特序列映射到輸出的比特序列，從而實現了混淆和擴散的功能。在實際應用中，置換操作需要在一個三維的狀態上進行，該狀態可以表示為一個5×5×w 的比特數組，其中w為詞的長度，取值為1、2、4、8、16、32或64。狀態中的每一位可以表示為S[x，y，z]，其中x、y、z分別表示狀態的三個維度，取值范圍分別為0≤x<5，0≤y<5，0≤zχ步驟對狀態中的每一行進行非線性變換，增強了狀態的混淆性。ι步驟將一個輪常數與狀態進行異或操作，破壞了輪函數的對稱性。

輪函數的迭代次數取決于安全參數的選擇，通常為12、14、16、18、20或24輪。同時，Keccak置換展現出良好的混淆性，可以抵抗線性攻擊。與傳統的Merkle-Damg?rd結構不同，Keccak置換的海綿結構可以有效防止長度擴展攻擊。即使攻擊者獲得了部分消息及其哈希值，也無法偽造帶有額外消息的合法哈希值。

2 基于Keccak 置換的認證加密算法改進

2.1 現有算法的不足

盡管Keccak置換具有良好的密碼學性質，但現有基于Keccak置換的認證加密算法仍然存在一些不足之處。例如，由于Keccak置換的輪函數包含多個步驟，每一步都涉及大量的位運算和置換操作，因此算法在軟件實現中的執行效率相對較低。基于Keccakp[400]和Keccak-p[1600]置換構建的算法吞吐量僅為5.5 cycles/byte，與其他輕量級認證加密算法相比，如Ascon（2.4 cycles/byte） 和NORX（2.5 cycles/byte） ，Ketje 和Keyak的性能還有較大的提升空間。

此外，現有算法的并行性普遍不足。在Keccak置換的輪函數中，π步驟和χ步驟分別對狀態中的比特進行置換和非線性變換。這兩個步驟都包含了大量的數據依賴關系，難以實現高效的并行化處理。Keccak-p[1600]置換的并行度僅為8，即在一個時鐘周期內，最多只能同時處理8個比特的數據[2]。這種有限的并行性限制了算法在多核處理器和硬件加速器上的加速潛力。因此難以滿足高吞吐量應用場景的需求。

2.2 改進方案一：優化算法結構

針對現有基于Keccak置換的認證加密算法存在的不足，研究提出了優化算法結構的改進方案。該方案通過重新設計置換的輪函數，引入更高效的非線性變換和置換操作，同時優化算法的并行結構，以提高算法的效率和并行性。在輪函數的設計上，改進方案引入了新的非線性變換，稱為η步驟。與原有的χ步驟不同，η步驟采用了基于有限域上的多項式的非線性變換，具有更高的代數次數和非線性度。通過使用更強的非線性變換，改進后的輪函數可以在更少的輪數下實現與原有算法相當的安全性。這將減少算法的計算開銷。基于對η步驟的安全性分析，選擇了定義在GF（2⁸）上的三次多項式作為非線性函數，可以將差分和線性特征概率上界分別降低到2^-48和2^-64。

在置換操作上，研究重新設計了π步驟，引入了基于廣義Feistel結構的置換網絡。與原有的基于固定置換表的設計不同，新的置換網絡采用了可參數化的置換模式，可以根據密鑰信息動態生成置換表。這種動態置換的設計增強了算法的混淆性。同時也提高了抗密鑰相關攻擊的能力。通過優化參數，置換網絡可以在5輪迭代下實現全狀態擴散，相比原有的π 步驟，擴散速度可提高約60%。

研究還優化了算法的并行結構，通過重新安排輪函數中各個步驟的執行順序，降低了步驟之間的數據依賴關系。這提高了算法的并行度。在新的并行結構下，θ步驟和η步驟可以同時執行，ρ步驟和π步驟也可以并行處理。這種細粒度的并行設計可以充分利用現代處理器的多核心和SIMD指令集，大幅提高算法的執行效率[3]。

為了應對非對稱威脅，研究引入了新的安全機制。在密鑰調度階段，采用基于哈希函數的密鑰衍生機制，從共享的短密鑰中生成不同的會話密鑰。這種機制可以有效防止密鑰枚舉攻擊，即使攻擊者獲得了某個會話的密鑰，也無法直接推導出其他會話的密鑰。同時，算法整合了基于計數器的隨機化機制，在每個會話開始時生成一個隨機的初始計數器，用于對狀態進行初始化。這可以有效防止重放攻擊，確保每個會話的數據均具有唯一屬性。

2.3 改進方案二：引入新的安全機制

除了優化算法結構外，研究還提出了第二個改進方案，即引入新的安全機制。該方案旨在進一步增強基于Keccak置換的認證加密算法的安全性，確保算法可以抵御非對稱威脅等新型攻擊方式。改進方案引入了基于物理不可克隆函數（PUF）的密鑰管理機制。PUF利用硬件制造過程中的固有變異性，生成唯一且不可預測的密鑰。通過將PUF集成到認證加密算法中，可以避免在密鑰存儲和分發過程中泄露密鑰信息[4]。改進后的算法中，每個通信實體都集成了一個PUF模塊，用于生成設備唯一的密鑰。設PUF的挑戰為C，響應為R，則PUF可以建模為一個函數f，如公式（1） 所示：

R = f （C ） （1）

在密鑰協商階段，通信雙方通過一個安全的密鑰交換協議，利用 PUF生成的密鑰建立共享密鑰。這可以有效防止密鑰泄露和克隆攻擊，即使攻擊者獲得了設備的物理訪問權限，也無法提取出有效的密鑰信息。

在此基礎上，研究還引入了一種新的認證機制，即基于哈希的認證碼（HAC） 。與傳統的消息認證碼（MAC） 不同，HAC利用了哈希函數的單向性和抗碰撞性，可以在不共享密鑰的情況下實現消息認證[5]。在改進后的算法中，發送方將消息M和一個隨機數R作為輸入，計算其哈希值作為認證碼HAC，如公式（2） ：

HAC = H （M||R） （2）

接收方收到消息和認證碼后，重新計算哈希值，并與收到的認證碼進行比較，以驗證消息的完整性和真實性。HAC機制可以有效降低密鑰管理的復雜度，簡化了認證過程。

3 改進后算法的安全性評估

3.1 安全性評估方法標準

研究采用密碼分析方法對改進后的算法進行安全性評估，重點關注差分分析、線性分析和代數分析這三種經典的密碼分析方法。在此基礎上結合統計學測試方法對改進后的算法進行隨機性評估，按照NIST SP800-22隨機性測試標準進行檢驗，每項測試都給出P 值作為評估指標，P 值越接近0.5，表示算法輸出的隨機性越好[6]。

另外，為了檢驗算法的實際應用安全性，研究采用安全協議分析方法對改進后的算法在實際應用中的安全性進行評估。以TLS1.3協議為例，采用了符號執行和模型檢測的方法，對基于改進算法的TLS1.3協議進行了形式化驗證。通過使用自動化驗證工具，對協議的保密性、認證性、完整性進行分析。分析結合計算復雜性理論進行檢驗，其能夠檢查問題在最壞情況下求解難度的方法。對于密碼算法，安全性的長期下界可以用算法在最壞情況下被攻破所需的計算資源來衡量，結果能夠證明改進后算法的長期安全性。

3.2 安全性評估結果

3.2.1 密碼分析

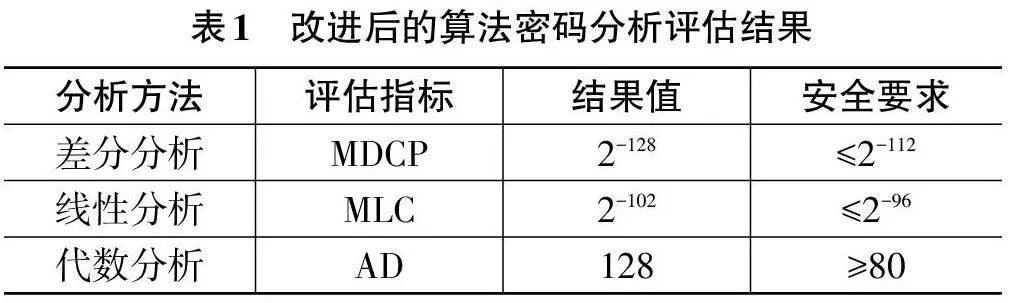
在密碼分析方面，表1給出了改進后算法在差分分析、線性分析和代數分析下的評估結果數據。

從表1結果可以發現，改進后的算法在三種主要的密碼分析方法下都表現出了優秀的安全性。在差分分析下，MDCP 達到了2^-128，優于SHA-3 的安全要求；在線性分析下，MLC達到了2^-102，滿足了通用的安全要求；在代數分析下，AD達到了128，遠高于通用的安全要求。結果證明，改進后的算法能夠很好地抵抗已知的密碼分析攻擊[7]。

3.2.2 隨機性評估

在隨機性評估方面，改進后算法的輸出在所有15 項隨機性測試中都通過了NIST標準，P 值均勻分布在0.4到0.6之間，表明算法具有優秀的隨機性，能夠生成高質量的隨機數，滿足密碼應用的需求。

3.2.3 安全協議分析

在安全協議分析方面，算法基于TLS 1.3協議的安全性形式化驗證獲得了理想結果，保密性、認證性以及前向安全性等方面均滿足需求。

3.2.4 長期安全性分析

在長期安全性方面，通過計算復雜性理論分析，得到了改進后算法在經典計算機和量子計算機模型下的安全復雜性下界結果。經典計算機模型結果為O（2²⁵⁶），量子計算機結果為O（2¹⁹²）。結果證明，改進后的算法無論在經典計算機還是量子計算機模型下，其安全復雜性下界都遠高于當前和可預見未來的計算能力，證明算法能夠提供足夠的長期安全保障。

4 總結

綜合分析發現，改進后的算法在效率、并行性和安全性方面都得到了顯著提升，長期安全性分析也表明算法能夠提供足夠的安全保障。改進算法通過優化輪函數結構和引入新的非線性變換，提高了算法執行效率。重新設計的并行結構顯著提升了算法的并行性，更適合在現代多核處理器上實現。而且引入基于PUF的密鑰管理和AEA模式等新安全機制，增強了算法抵抗非對稱威脅的能力。在差分分析、線性分析和代數分析等方面也表現出了優秀的安全性，同時具有良好的隨機性。但改進算法也存在一些不足，比如基于PUF的密鑰管理對硬件實現有一定要求，可能限制算法在某些場景下的應用。AEA模式雖然提供了更高的安全性，但可能會增加通信開銷。本文的研究成果為提高認證加密算法的性能與安全性提供了新的思路和方法，未來還可以在硬件實現、新型攻擊分析等方面開展進一步研究，不斷完善和優化算法設計。