一種針對駐留轉換雷達的信號分選算法

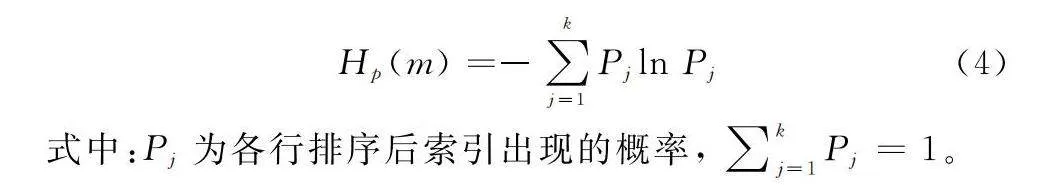
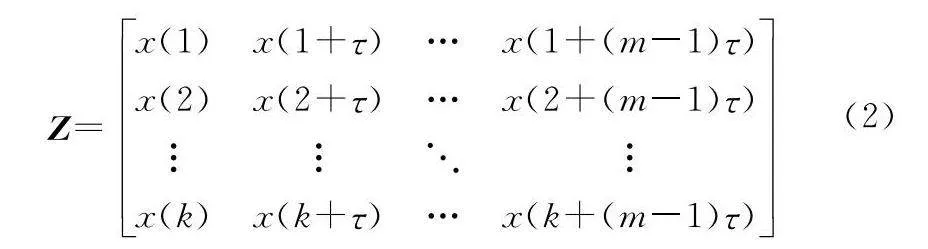
摘要： 復雜電磁環境下駐留轉換雷達的信號分選是制約電子偵察技術發展的瓶頸，由于其復雜多變的成形規律，信號子周期難以被檢測;脈沖重復周期調制類型不明，脈沖序列無法成功提取;提取的多個子周期脈沖序列無法合并為一部雷達信號，造成虛警。針對以上問題，提出一種針對駐留轉換雷達的信號分選算法，利用雙門限提高子周期檢測概率，通過霍夫變換結合迭代自組織聚類判斷信號是否屬于駐留轉換雷達，改進搜索算法以提取脈沖序列，依據排列熵指標將多脈沖序列合并為一部駐留轉換雷達信號。仿真實驗結果表明，所提算法在25%脈沖丟失率的復雜電磁環境下，可以將三部駐留轉換雷達信號成功分選。

關鍵詞： 駐留轉換; 信號分選; 霍夫變換; 脈沖序列搜索; 排列熵

中圖分類號： TN 971.1

文獻標志碼： A

DOI：10.12305/j.issn.1001-506X.2024.06.10

Signal deinterleaving algorithm for dwell and switch radar

ZHANG Chunjie^1，2， QING Song^1，2， DENG Zhian^1，2，*， LIU Yuchen³

（1. College of Information and Communication， Harbin Engineering University， Harbin 150001， China; 2. Key Laboratory of Advanced Marine Communication and Information Technology， Ministry of Industry and Information Technology， Harbin 150001， China; 3. Harbin Power Supply Company， State Grid Heilongjiang Electric Power Company Limited， Harbin 150001， China）

Abstract： The signal deinterleaving of dwell and switch radar in complex electromagnetic environments is a bottleneck that limits the development of electronic reconnaissance technology. The signal sub-cycles are difficult to be detected due to their complex and variable forming laws. The pulse sequences cannot be successfully extracted due to the unknown pulse repetition period modulation type， and the 1 alarms caused by extracted multiple sub-cycle pulse sequences that cannot be combined into one single radar signal. To address the above problems， a signal deinterleaving algorithm is proposed for the dwell and switch radar. The proposed algorithm enhances the detection probability of signal sub-cycles with double-threshold method， and the Hough transform is combined with iterative self-organizing clustering to determine whether the signal belongs to the dwell and switch radar， improving the search algorithm to extract pulse sequences， and combining multiple pulse sequences into one dwell and switch radar signal based on the permutation entropy index. Simulation experiments show that the proposed algorithm can successfully deinterleave the three dwell and switch radar signals in a complex electromagnetic environment with a pulse loss rate of 25%.

Keywords： dwell and switch; signal deinterleaving; Hough transform; pulse sequence search; permutation entropy

0 引 言

隨著雷達技術的飛速發展^［1］，電磁戰場雷達輻射源密度大大增加^［2］，新穎雷達信號脈沖重復間隔 （pulse repetition interval， PRI）調制類型的出現更是給電子偵察任務帶來了嚴峻的挑戰^［3］。雷達信號分選是電子偵察中的核心技術，分為多參數聚類分選與單參數PRI分選兩部分，首先通過聚類^［4-5］手段依據多參數信息將多維電磁空間劃分為多個子空間，再通過到達時間 （time of arrival， TOA）提取PRI完成雷達信號分選^［6］。然而隨著駐留轉換雷達信號的出現，即使經過多參數聚類對電磁空間的稀釋，傳統的單參數分選算法仍無法將其分選。如何在復雜電磁環境中，利用PRI參數分選出駐留轉換雷達信號，并將其脈沖分離提取，是實現電磁頻譜感知的重要一環^［7］。

常見的單參數分選算法如累積差直方圖 （cumulative difference histogram， CDIF）^［8］、序列差直方圖 （sequential difference histogram， SDIF）^［9］以及PRI變換法^［10］等，僅能較為有效地分選固定、參差以及小抖動等雷達信號，對復雜類型雷達信號分選效果差^［11］。近年來，有多位學者嘗試在算法結構上進行改進^［12］，將其與語義分割^［13-14］、深度森林^［15］等人工智能前沿技術相結合，從而實現對復雜類型雷達信號的分選，但目前仍缺少算法能在多部雷達信號混疊的情況下實現駐留轉換雷達信號的分選。

PRI調制類型識別是雷達信號分選中的重要一環^［16］，成功識別PRI調制類型是脈沖序列搜索的基礎。文獻［17-18］分別使用前饋神經網絡、自相關函數等方法對駐留轉換雷達信號進行PRI調制類型識別，取得了較好效果。文獻［19］則采用遞歸神經網絡進行識別，對序列識別效果更明顯。文獻［20］將雷達脈沖序列轉換為符號序列進行識別。但以上文獻均是對完整單一雷達信號進行識別，需要提前將其脈沖提取完成，實現脈沖提取與類型識別的統一尤為重要^［21］。

傳統的脈沖提取通過PRI增減在一定范圍內抽取，無法勝任復雜類型雷達信號的搜索，文獻［22］利用雙閾值搜索抖動雷達信號，但閾值仍需人為設定，且無法針對大抖動、滑變雷達信號、駐留轉換雷達信號等復雜雷達信號進行搜索。文獻［23］則將生物信息學技術引入脈沖序列搜索。文獻［24］將聚類思想引入序列搜索。文獻［25］將密度聚類應用于序列搜索，提取出30%大抖動雷達信號序列，但仍未實現針對駐留轉換雷達信號的脈沖序列搜索。

本文針對復雜電磁環境下駐留轉換雷達信號分選時出現的一系列問題，對傳統算法進行改進，并與新技術相融合，提出一種針對駐留轉換雷達的信號分選算法。該方法利用雙門限提高子周期PRI檢測概率，通過霍夫變換結合迭代自組織聚類判斷信號是否屬于駐留轉換雷達信號類型，利用改進搜索算法提取其脈沖序列，最后依據排列熵指標將多脈沖序列合并為一部駐留轉換雷達信號。仿真實驗結果表明，該方法可在復雜電磁環境下將駐留轉換雷達信號成功分選。

1 基本理論

1.1 駐留轉換雷達信號

雷達信號PRI調制類型是進行雷達信號分選所需的必要參數^［26］，只有掌握了雷達信號的PRI調制類型，才能根據PRI值在電磁空間進行脈沖序列搜索，實現該雷達信號最終的成功分選，把該雷達信號的各維度信息從電磁空間中剔除。

雷達信號PRI調制類型多種多樣，各種新穎的調制類型層出不窮^［27］，但其調制類型基本不超出以下5種：固定、參差、抖動、滑變以及駐留轉換雷達信號^［28］。其中，駐留轉換雷達信號由于其PRI值的隨機性以及駐留時間的不確定性，大大增加了雷達信號分選的難度。

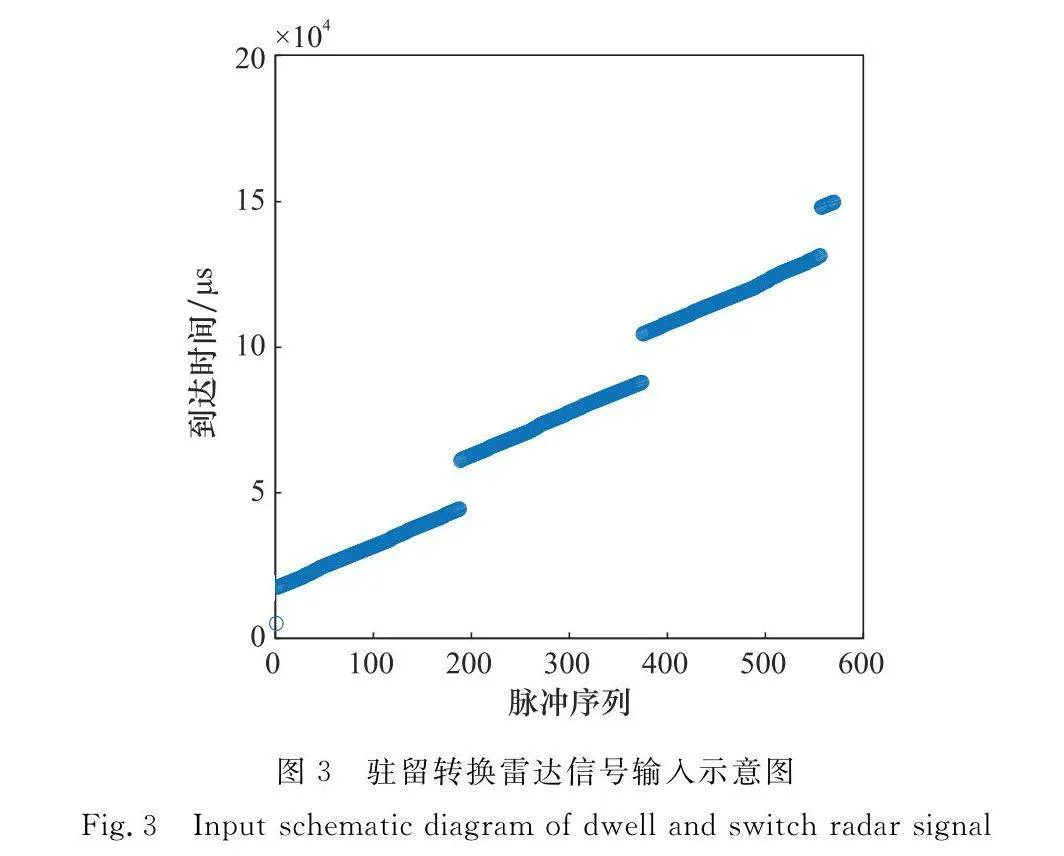
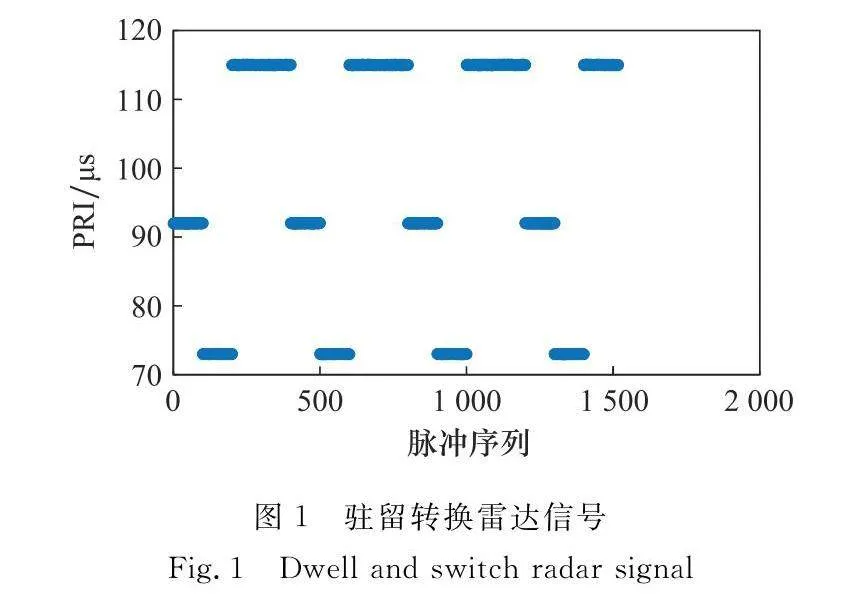
駐留轉換雷達信號是同時具備PRI駐留與PRI轉換兩種特點的一類雷達信號，PRI的駐留特點是指在該子周期時間段內雷達信號PRI參數保持恒定，而PRI轉換則是指在一個完整的駐留轉換周期內雷達信號PRI會在幾個特定的值之間轉換。駐留轉換雷達信號的每個子周期的PRI值都為常量。區別于參差雷達信號，駐留轉換雷達信號的子周期PRI需駐留一段時間并保持一定脈沖個數后，再切換為另一個子周期的PRI值。駐留轉換雷達信號如圖1所示。

以圖1駐留轉換雷達信號為例，子周期PRI₁～PRI₃分別為92 μs、73 μs、115 μs，駐留時間分別為100、100、200個脈沖點。一個整體大周期時間T的時長如下表示

T=100PRI₁+100PRI₂+200PRI₃（1）

1.2 駐留轉換雷達信號分選挑戰

駐留轉換雷達信號的出現，給現有的電子偵察系統帶來了極大的挑戰。在復雜電磁環境中，子周期PRI值無法被檢測到;無法掌握PRI調制類型，導致脈沖序列搜索無法繼續;即使進行了脈沖序列搜索，也無法在搜索到的各脈沖序列里進行關聯，導致虛警率上升。

1.2.1 子周期PRI檢測概率低

PRI是單參數信號分選中需要獲取的首要參數，因此想成功分選出駐留轉換雷達信號，就必須獲得其各子周期的PRI。然而由于其轉換特性，一個完整周期內包含多個子周期，分布分散，導致各子周期PRI的檢測概率大大降低，加大了駐留轉換雷達信號的分選難度。

1.2.2 脈沖序列提取困難

脈沖序列搜索提取是單參數信號分選中的重中之重，沒有脈沖序列搜索提取，就無法將目標雷達信號從電磁空間中剔除。失敗的脈沖序列提取，會導致大量脈沖殘留，嚴重影響其他雷達信號的分選工作。而駐留轉換雷達信號復雜的成形規律導致搜索時僅能針對單一子周期PRI進行搜索，但即使是只針對單一子周期PRI序列進行搜索，也無法采用與固定雷達信號相同的方法，因為駐留時間未知，會造成大量誤搜索。更何況在實際分選的復雜電磁環境中，無法辨別該子周期是否屬于駐留轉換雷達信號。

1.2.3 多子周期虛警現象

當電磁空間中僅有一部駐留轉換雷達信號時，搜索到的駐留轉換雷達信號子周期序列脈沖僅可能為同一部。但當面對復雜電磁環境時，若存在多部駐留轉換雷達信號，則搜索到的子周期序列無法判別其歸屬，各子周期脈沖相互獨立，這既造成了虛警現象，也并沒有實現真正分選出駐留轉換雷達信號的目的。

2 駐留轉換雷達信號分選算法

為解決復雜電磁環境下駐留轉換雷達信號分選時的一系列難題，提高復雜電磁環境下子周期PRI檢測性能，增大脈沖搜索成功率，實現子脈沖序列合并，本文提出一種針對駐留轉換雷達信號的信號分選算法。

2.1 駐留轉換雷達信號分選框架

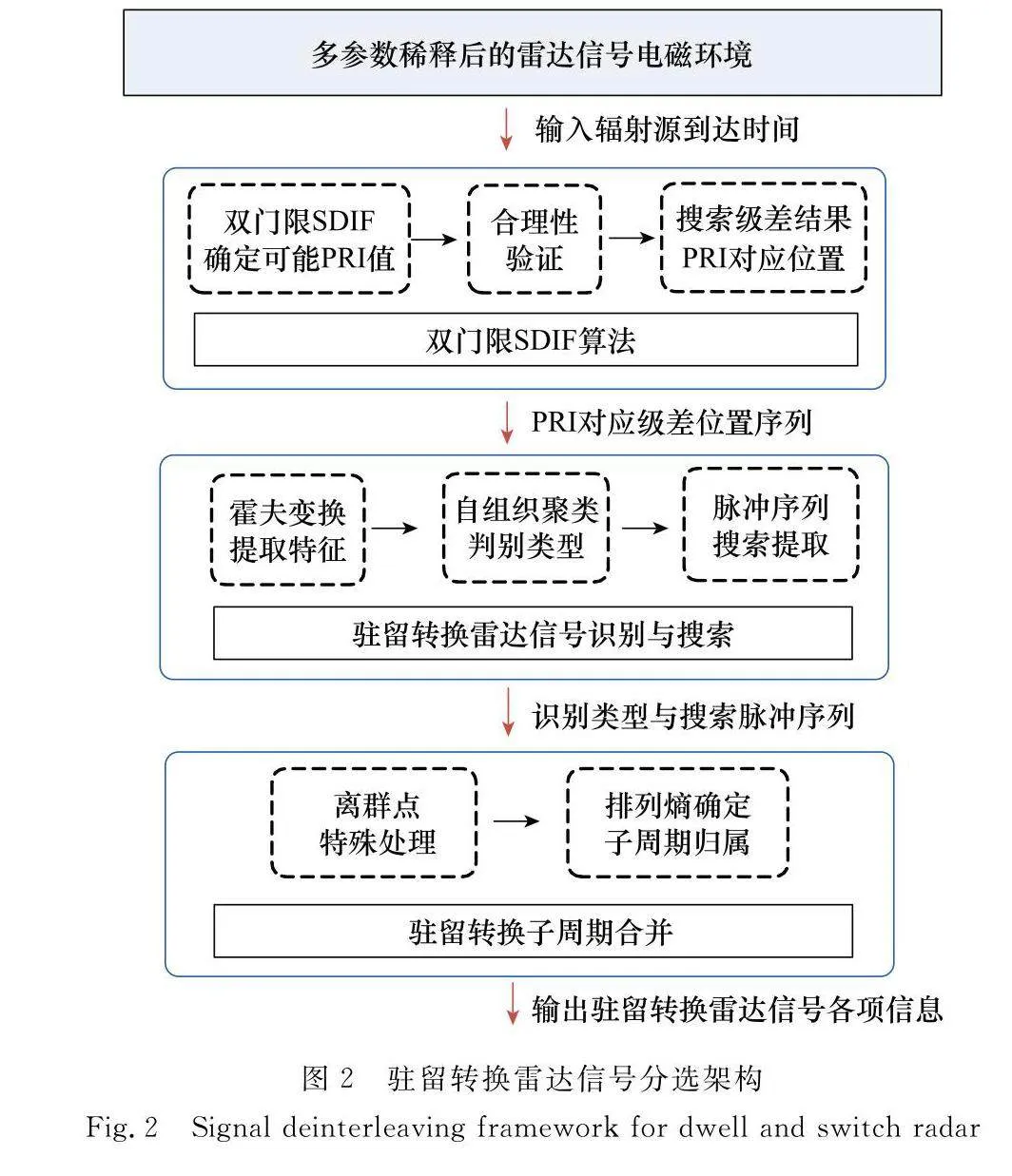
在復雜電磁環境中，即使經過多參數聚類稀釋，電磁空間仍有可能包含固定、參差、抖動、滑變以及駐留轉換等多類型雷達信號。因此，本文提出的駐留轉換雷達信號分選算法的意義是將駐留轉換雷達信號從電磁空間中篩選出來并進行分選剔除，是基于雷達信號綜合分選算法大框架提出的^［6］，圖2是本文提出的駐留轉換雷達信號分選框架。

如圖2所示，電磁空間內的雷達信號通過雙門限SDIF算法增大檢測性能，檢測可能的PRI，依據可能的PRI峰值獲取PRI對應的脈沖位置信息;將脈沖位置信息序列進行霍夫變換，結合迭代自組織對霍夫空間數據點進行聚類，依據聚類簇個數分析該PRI對應序列是否屬于駐留轉換雷達信號，運用改進的序列搜索算法實現針對該駐留轉換雷達PRI序列的提取;待各PRI序列提取完畢后，首先對其進行離群點特殊處理，防止離群點分布影響后續排列熵的計算，通過計算各組合間的排列熵，選擇排列熵最小的組合，該組合內的各PRI子序列則同屬于一部駐留轉換雷達信號。

2.2 雙門限SDIF算法

PRI是脈沖雷達信號中的重要參數，絕大部分單參數信號分選算法的首要目的都是獲得目標雷達信號的PRI相關信息，再依據PRI信息進行后續搜索等處理。

由于駐留轉換雷達信號的特殊性，無法將一部駐留轉換雷達信號當作一個整體來進行分選，得到整體周期的總體PRI或者其PRI大致變換范圍都無助于分選結果，因此只能將駐留轉換雷達信號按子周期劃分，依次對子周期進行分選。

雙門限SDIF首先由文獻［6］提出，在原始SDIF基礎上設計雙門限提升高丟失率下PRI的檢測概率，在分選駐留轉換雷達信號子周期時，仍可取得較好效果。

采用雙門限，在提高PRI檢測概率的同時，也增大了PRI的虛警率，因此需通過PRI合理性進行驗證，當連續出現多個符合該PRI的脈沖時，即判定為合理，并采用CDIF方法搜索級差結果中等于該PRI的脈沖位置。為防止由于脈沖混疊情況而導致脈沖位置搜索不全，在多級差結果間進行搜索并累積。累積得到的該PRI對應脈沖級差位置將作為下一模塊駐留轉換信號識別與搜索的輸入，用于分辨該子周期是否屬于駐留轉換雷達信號。

2.3 駐留轉換信號識別與搜索

駐留轉換雷達信號的識別與搜索是本文所提算法的核心，由于本模塊駐留轉換信號識別的最終目的是將該目標雷達信號從電磁空間中剔除，因此與其他文獻中針對完整周期的脈沖序列進行PRI調制類型識別不同。本文則是利用上一模塊的PRI對應脈沖級差位置序列通過霍夫變換結合自組織聚類，針對PRI子周期序列成形規律進行分析，判斷其是否屬于駐留轉換雷達信號。

本節首先針對輸入特征進行預處理，增強特征，之后利用霍夫變換從中提取直線特征，配合自組織聚類得到該PRI序列成形規律，從而判斷其是否為駐留轉換雷達信號，最后憑借針對駐留轉換雷達信號的脈沖序列搜索算法盡可能將其脈沖序列從電磁空間中剔除。

2.3.1 輸入特征預處理

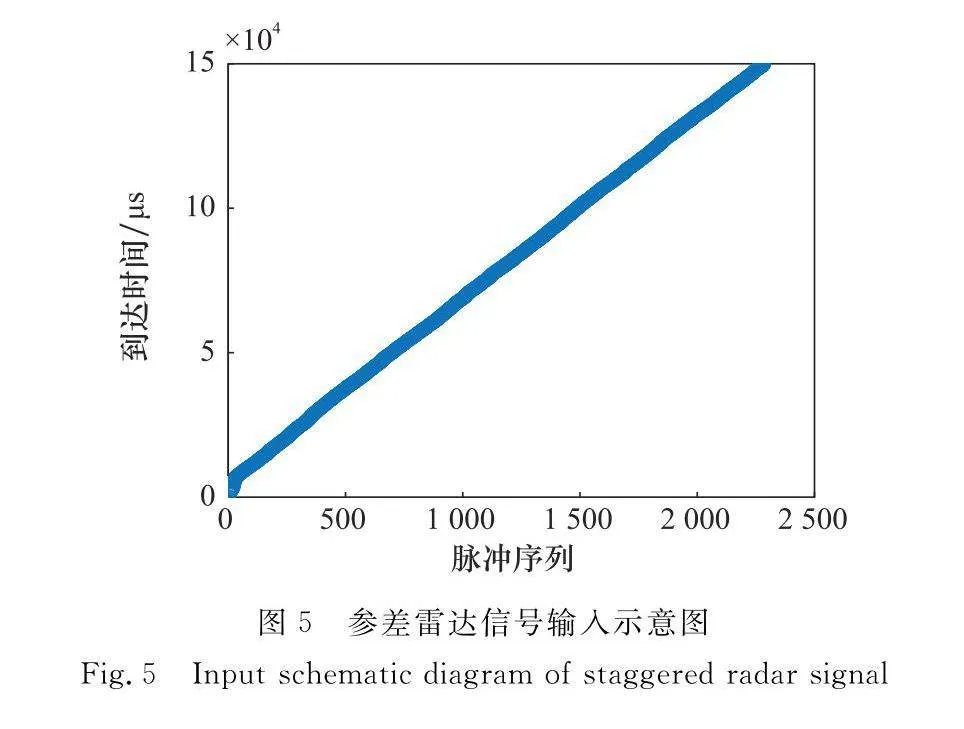
在第2.2節模塊中獲得的PRI對應脈沖級差位置序列存在多種表現形式，每個脈沖也對應著多個參數信息，為充分體現駐留轉換雷達成形特征，將一維序列延伸為二維信息，橫坐標為脈沖索引，縱坐標則為位置序列對應脈沖的到達時間，如圖3所示，以充分體現其駐留轉換的特性。而按同種方式獲得的固定、參差雷達信號相關二維信息如圖4和圖5所示。由圖4和圖5分析可知，非駐留轉換雷達信號的PRI對應級差結果位置序列大體相同，若掌握輸入二維數據圖中直線段個數，則能區別其是否為駐留轉換雷達信號。

2.3.2 霍夫變換提取特征

如前文所提，駐留轉換雷達信號識別的關鍵在于能否識別出二維數據圖中直線段數。霍夫變換是從圖像中識別幾何圖形的一種基本方法，如直線、圓、橢圓等。

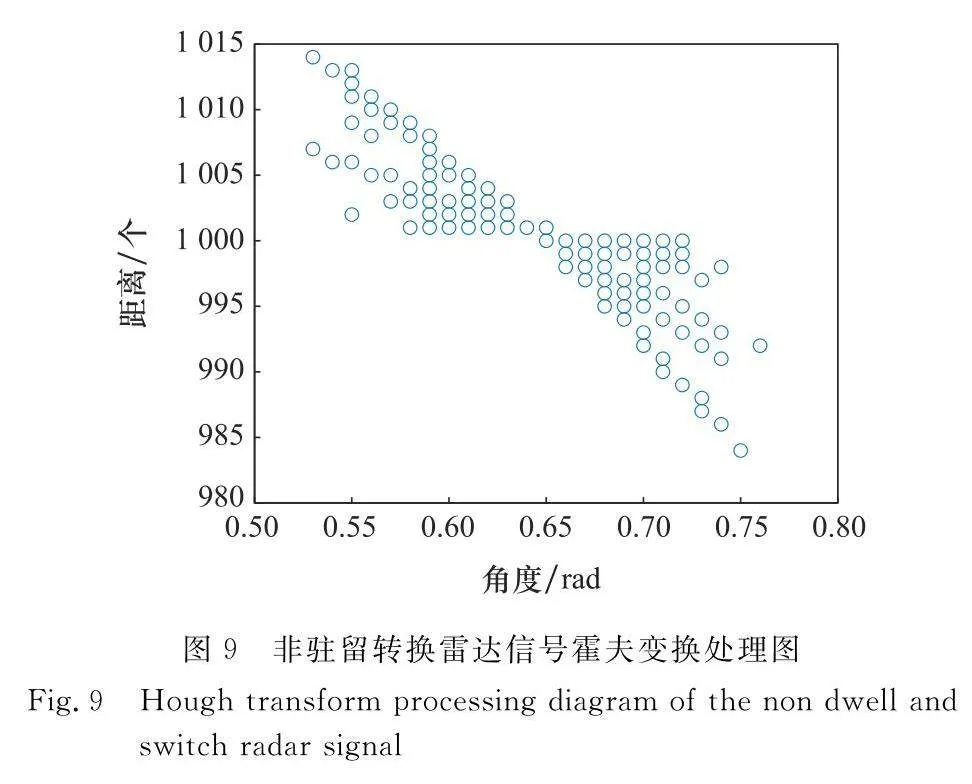
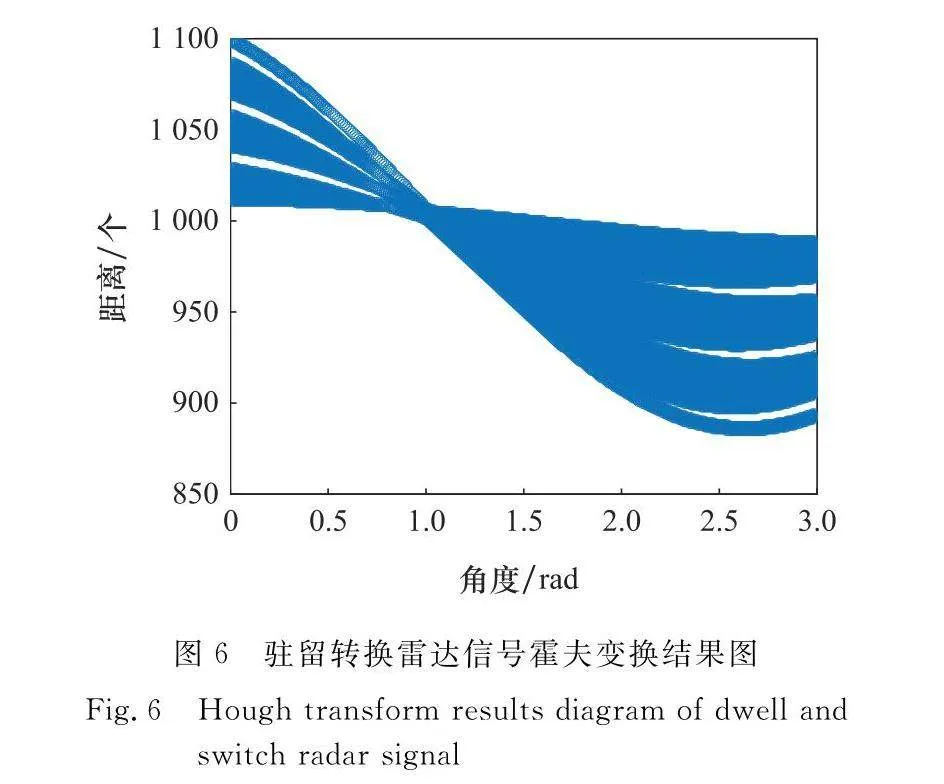
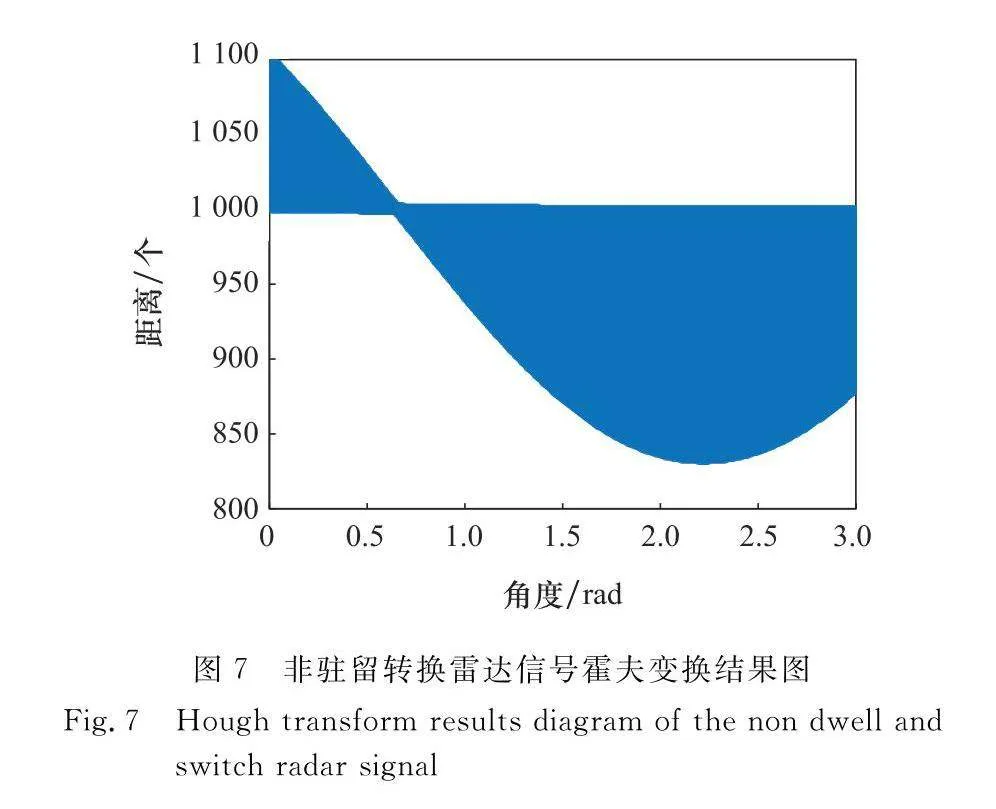
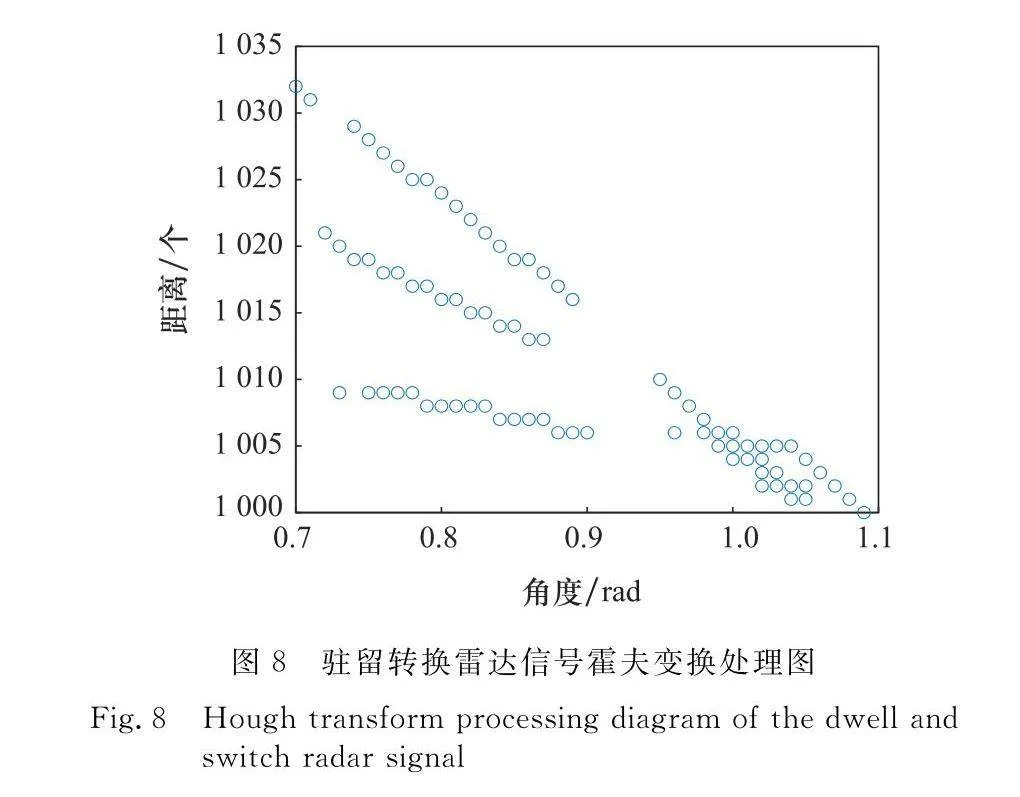
一條直線可以有兩種表示方法，即常見的笛卡爾坐標表示法與霍夫空間，霍夫空間又稱為極坐標空間。通過極坐標變換可將笛卡爾坐標系中的直線轉變為霍夫空間中的一個點;反之，笛卡爾坐標系中的一個點在霍夫空間中便是一條直線。因此，通過將二維數據圖中各點笛卡爾坐標進行霍夫變換，首先將霍夫空間網格離散化，再在霍夫空間中將各部分直線結果累加，局部最大值點便為一條直線。然而在實際情況中，局部最大值點的選取較為困難，圖6和圖7分別為駐留轉換雷達信號與非駐留轉換雷達信號的霍夫變換結果圖，從圖中可知，線束密度高，尋找局部最大值點較為困難，難以確定局部極大值點的個數。

本文遵循統計學方法，按照最大值百分比設定閾值，只留存閾值以上的霍夫空間坐標點，使局部極大值點更加明顯，同時也極大程度地減輕了后續聚類算法的運算量。圖8和圖9分別為駐留轉換雷達信號與非駐留轉換雷達信號處理后的霍夫變換結果圖，從中可以觀察到聚類簇數與直線段數呈正相關。

2.3.3 自組織聚類判別PRI調制類型

選擇合適的聚類方法，對于取得更好的識別效果來說，事半功倍。自組織聚類是非監督動態聚類中的一種，改進于k-means聚類算法，在樣本全部調整一次之后才重新計算樣本均值，節約了時間;而且其加入了“合并”以及“分裂”等操作，可根據預設聚類數動態進行調整，獲得合理聚類結果。

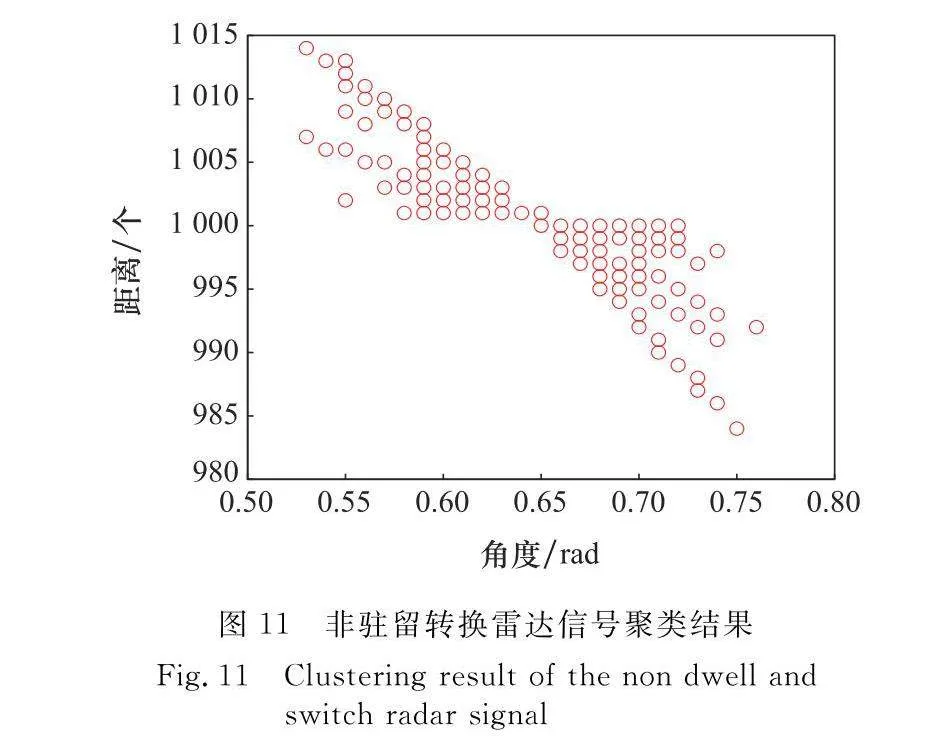
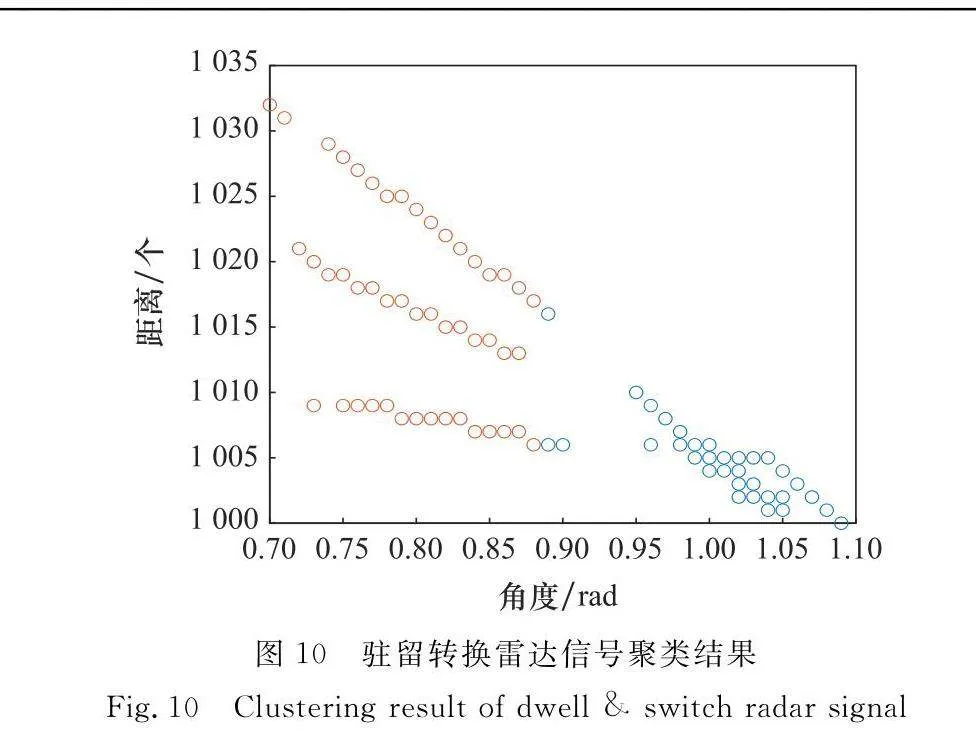
為提高最終駐留轉換雷達信號子周期識別率，將聚類結果分為兩種情況，一是聚類結果唯一，則代表輸入二維數據圖中僅存在一條完整直線，判斷為非駐留轉換雷達信號;二是聚類結果為多類，說明存在多條直線，符合駐留轉換雷達信號特征。

圖10和圖11分別為駐留轉換雷達信號與非駐留轉換雷達信號的自組織聚類結果圖，如圖所示，自組織聚類方法效果良好，根據聚類結果可以較為容易地辨別駐留轉換雷達信號。

2.3.4 脈沖序列搜索提取

雷達脈沖序列的成功搜索提取與否，代表著該雷達信號是否真正從當前電磁環境中被剔除，不會被繼續遺留而干擾后續分選。由于駐留轉換雷達信號脈沖序列駐留時間不確定，無法將其分段按照固定雷達信號方式提取，而且其PRI變化復雜，不能提前獲得各子周期具體PRI，因此在搜索提取時，依舊是針對其中某一子周期進行搜索。

即使是按照固定雷達信號脈沖搜索方法依據單一PRI間距在脈沖序列中依次搜索，由于其他子周期空缺導致的大段脈沖序列空缺，仍會導致搜索方向偏離，既沒有搜索到真正需要的脈沖序列，也提取了很多其他不相干雷達的脈沖。

本文針對原始固定雷達信號搜索算法進行改進，將雙門限SDIF算法中PRI對應級差脈沖位置序列作為搜索起點備選集合，并引入合適的搜索終止機制，確保當搜索偏離時，及時切換搜索起點，保證在盡可能地搜索到更多脈沖的同時，防止不相干其他脈沖的誤搜索。

2.4 駐留轉換信號子周期合并

駐留轉換雷達信號子周期的合并是整個駐留轉換雷達信號分選任務的收尾，只有實現了各駐留轉換雷達信號所屬子周期的一一合并，才算將該駐留轉換雷達信號真正完成分選，而不是只針對電磁空間中僅有一部駐留轉換雷達信號的簡單情況。

本文選擇排列熵指標用于衡量各子周期間的相關程度，由于TOA特征不明顯，因此針對子周期TOA序列的一級差計算排列熵，并配合離群點特殊處理，防止脈沖丟失造成影響，使排列熵結果更符合實際情況，從而將同屬于一部駐留轉換雷達信號的子周期一一合并。

2.4.1 排列熵原理

排列熵是一種度量時間序列復雜度的指標，被廣泛應用于智能故障檢測診斷^［29-30］以及電力系統數字化建設中^［31］，適用于檢測時間序列隨機性或動力學突變行為，因此更適合檢測不同屬駐留轉換雷達信號子周期間由于駐留時間不匹配造成的異變，熵值越大，代表時間序列復雜程度越高，越不容易歸為一類同屬駐留轉換雷達信號^［32］。

設時間序列一級差序列為x（i），i為序列索引，i=1，2，…，N，N為序列總長，引入嵌入維數m與延遲序列索引τ對該時間序列進行重構，重構結果矩陣如下所示：

式中：矩陣中的一行代表一個重構分量，矩陣共有k=N－（m－1）τ行，m列。然后，對每一行內部各元素進行升序排列，若兩元素相等，則按原始順序下標進行排序，由此便得到了該行的符號序列S_l={j₁，j₂，…，j_m}，其中j₁，j₂，…，j_k為各元素在排序前相空間的列索引，l=1，2，…，k且k≤m！。在k行元素排序完成后，重構結果中的每一行都被映射到了S_l中，即m！個排列中的一種。

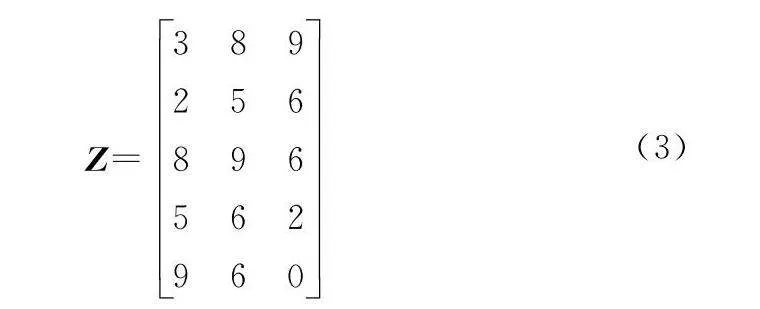
假設有一組時間序列{3，9，2，6，8，6，3，2}，按照嵌入維數3與序列延遲2重構矩陣，如下所示：

對每一行升序排列，返回其索引，如［3，2，8］排序后索引為［1，0，2］;［9，6，6］排序后索引為［2，0，1］。排列熵公式定義為

H_p（m）=-∑kj=1P_jln P_j（4）

式中：P_j為各行排序后索引出現的概率，∑^k_j=1P_j=1。

再對H_p（m）進行歸一化，得到：

H_p=H_P（m）ln（m！）（5）

由此，便得到了該子周期組合的排列熵值，但在實際情況下，由于脈沖丟失導致個別差值嚴重偏離平均值，需采取方法對離群點進行處理，才能得到正確反映子周期歸屬的排列熵。

2.4.2 離群點特殊處理

離群點特殊處理的關鍵是如何劃分離群點，如果一段時間序列中未出現嚴重脈沖丟失現象，卻強制進行離群點處理，會導致效果適得其反。然而，目前難以對整體脈沖丟失情況進行預估，因此需要一種方法可在無論丟失與否的情況下自適應地進行離群點處理。

本文提出一種針對駐留轉換類型信號的新離群點處理方法，首先依據平均值與標準值，在其子周期組合時間序列一級差結果中標記出相應離群點，之后將離群點偏離程度與均值進行比較，將離群點剔除，并在該位置加入一串自適應序列，自適應序列是一串由n個元素組成的以負平均值為間隔的遞減等差數列，n為離群點值/平均值的向上取整，起始值為離群點值。通過插入自適應序列，有效提高了排列熵對于不同屬子周期間的時序混疊及時序空白情況的敏感度，實現了子周期間同一部駐留轉換雷達信號的合并。

3 仿真實驗與性能分析

3.1 子周期PRI檢測效果分析

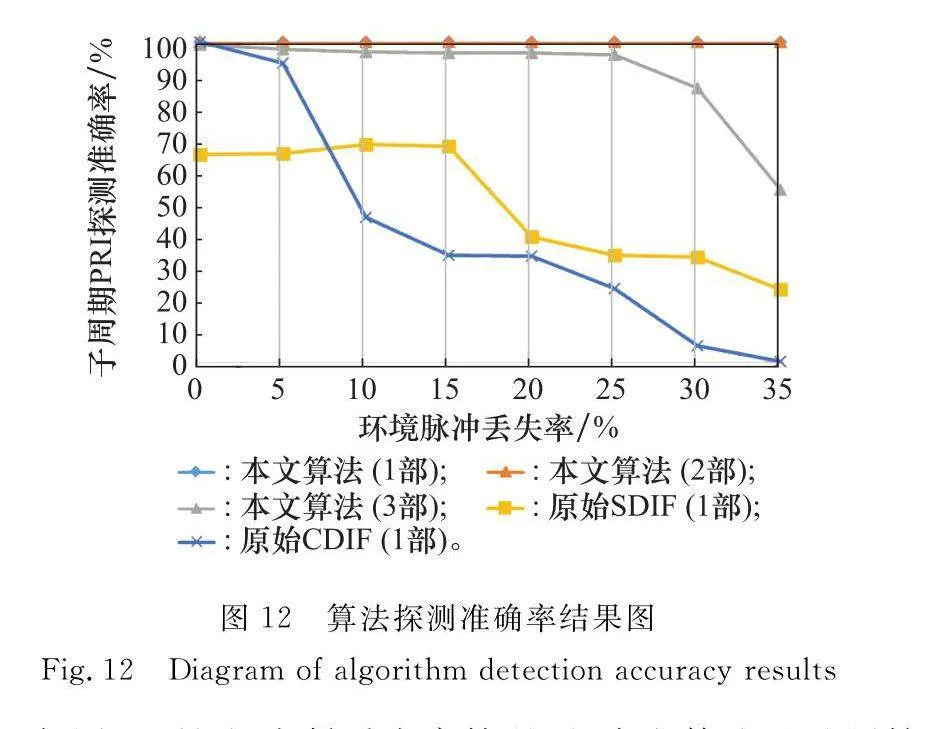
子周期PRI檢測性能優劣決定著算法的基礎。仿真3種電磁環境，分別包含1部、2部、3部駐留轉換雷達信號，子周期數分別為3、3、4，子周期PRI在20～200 μs內隨機選擇，同一部雷達信號各子周期間隔不小于20 μs，子周期駐留時間在100、150、200、250、300個脈沖點間隨機選擇，除PRI外其他參數完全相同，電磁環境脈沖丟失率選擇為0%至35%中的共8種電磁環境脈沖丟失率，分別選擇本文算法、原始SDIF與原始CDIF這3種算法對空間內雷達信號進行分選，對8種情況各進行1 000次蒙特卡羅仿真實驗，共8 000次。其中，原始SDIF與原始CDIF兩種算法對2部、3部情況分選效果不佳，因此忽略。算法中相同參數設置相同，本文算法中雙門限SDIF第2門限設置為第1門限的20%，算法探測準確率如圖12所示。

如圖12所示，在低丟失率情況下，本文算法以及原始CDIF取得了較好的效果。隨著丟失率增大，各算法總體探測準確率下降，其中原始SDIF算法對駐留轉換雷達信號檢測效果不好，在低丟失率時仍效果不佳;3種算法中本文算法下降趨勢最為緩慢，具有較高的分選準確率。

3.2 駐留轉換雷達信號識別效果分析

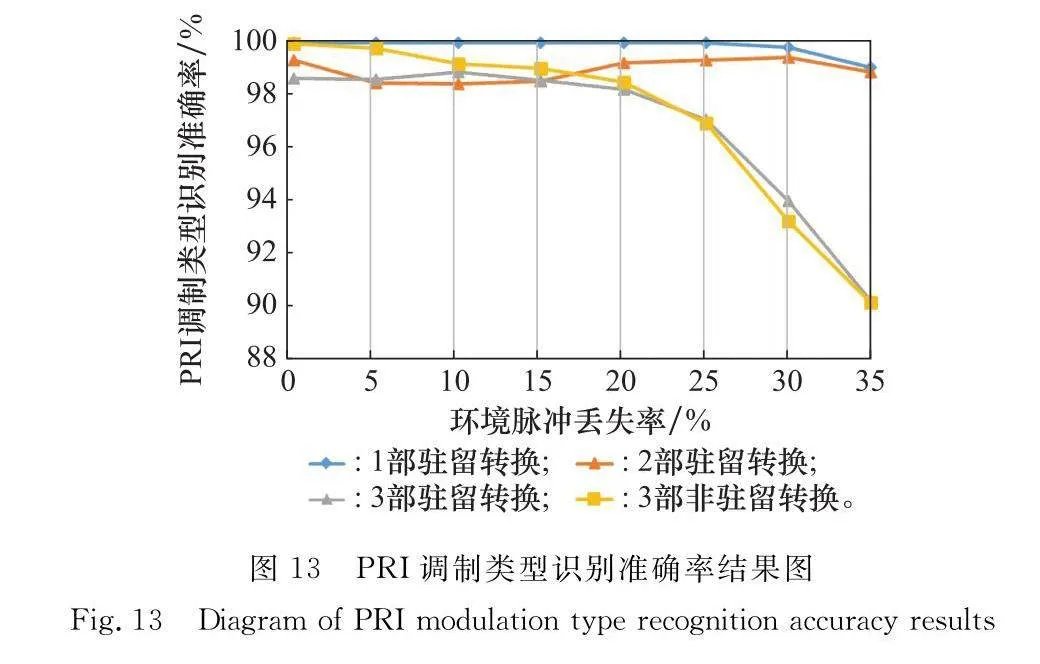
仿真4種電磁環境，分別包含1部、2部、3部駐留轉換雷達信號以及3部非駐留轉換雷達信號，子周期數分別為3、3、4，駐留轉換雷達信號參數設置與第3.1節一致，非駐留轉換雷達為2部固定雷達信號及1部參差雷達信號，固定雷達信號和參差雷達信號子周期PRI在50～200 μs間隨機選擇，除PRI外其他參數完全相同，電磁環境脈沖丟失率依舊選擇為0%至35%中的共8種，觀察識別準確率，在4種情況下對8種情況各進行1 000次蒙特卡羅PRI調制類型識別實驗，共32 000次，PRI調制類型識別準確率如圖13所示。

如圖13所示，在4種情況下，本文算法駐留轉換雷達信號識別準確率較高，均達到了90%以上。其中，當面對3部雷達信號的復雜環境進行判別時，由于電磁環境復雜脈沖丟失率較大，判別正確率下降速度略大;在1部、2部雷達信號環境時，丟失率對其影響并不大;當面對2部、3部駐留轉換雷達信號識別時，丟失率的提高，會適當減輕各雷達信號間的混疊程度，因此會使識別準確率有些許提高。

3.3 脈沖序列搜索效果分析

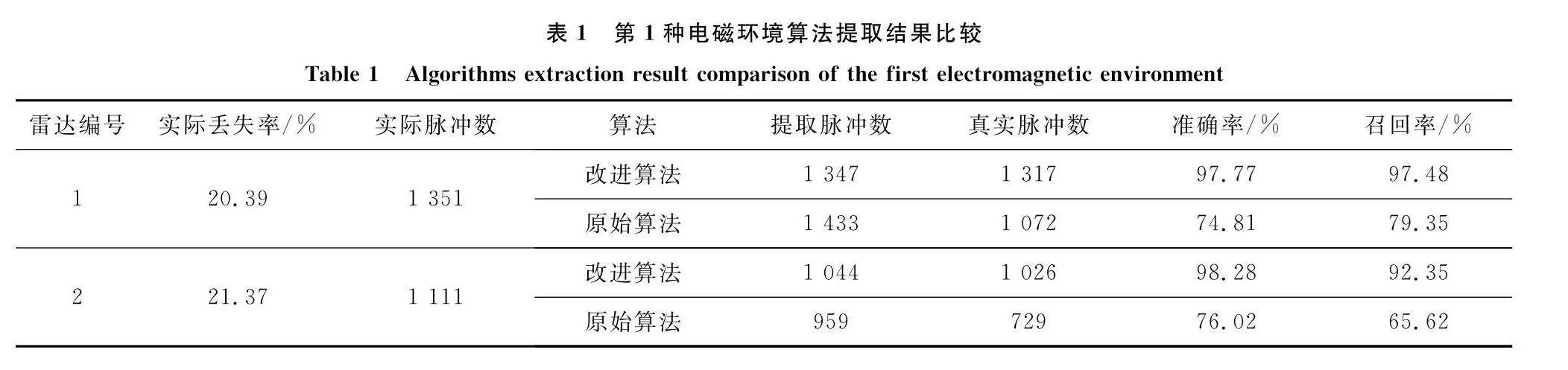
設置兩種電磁環境仿真測試脈沖序列搜索效果，第1種電磁環境包含2部駐留轉換雷達信號，其一子周期分別為40 μs、90 μs、133 μs，駐留時間分別為200、250、300個脈沖點，其二子周期為73 μs、92 μs、135 μs，駐留時間分別為100、100、200個脈沖點。整體仿真時間為150 000 μs，環境丟失率設置為20%，添加5%的隨機噪聲。第2種電磁環境在第1種基礎上再加入1部駐留轉換雷達信號，子周期分別為30 μs、50 μs、75 μs、140 μs，駐留時間分別為100、150、200、250個脈沖點，其他環境參數相同。

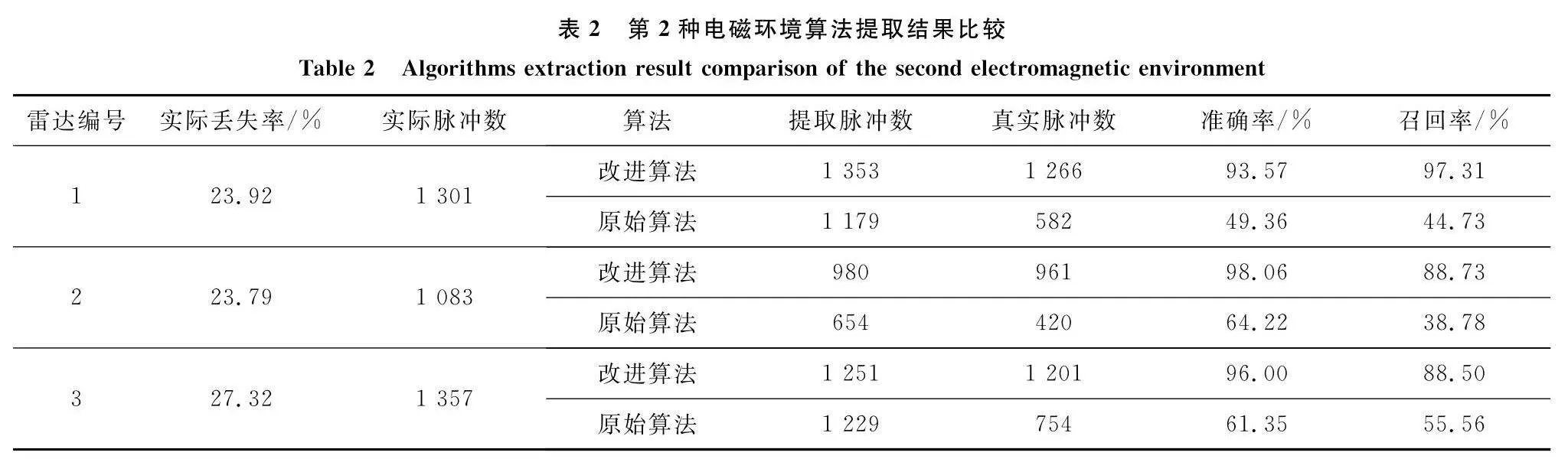
采用本文算法與傳統搜索算法進行對比，兩種電磁環境序列搜索結果分別如表1和表2所示。其中，準確率代表在提取到的脈沖中真實脈沖個數與所提取脈沖個數的比值，而召回率則代表在提取到的脈沖中真實脈沖個數與該信號在整體電磁環境中實際真實脈沖個數的比值。

如表1和表2所示，在包含2部、3部駐留轉換雷達信號的復雜電磁環境下，本文算法中的改進序列搜索算法可以在復雜電磁環境下完成針對駐留轉換雷達信號脈沖的提取，受電磁環境復雜度影響較小，準確率及召回率等指標均大幅領先原始算法，證明了本文算法在脈沖序列搜索方面的優異性能。

3.4 子周期合并效果分析

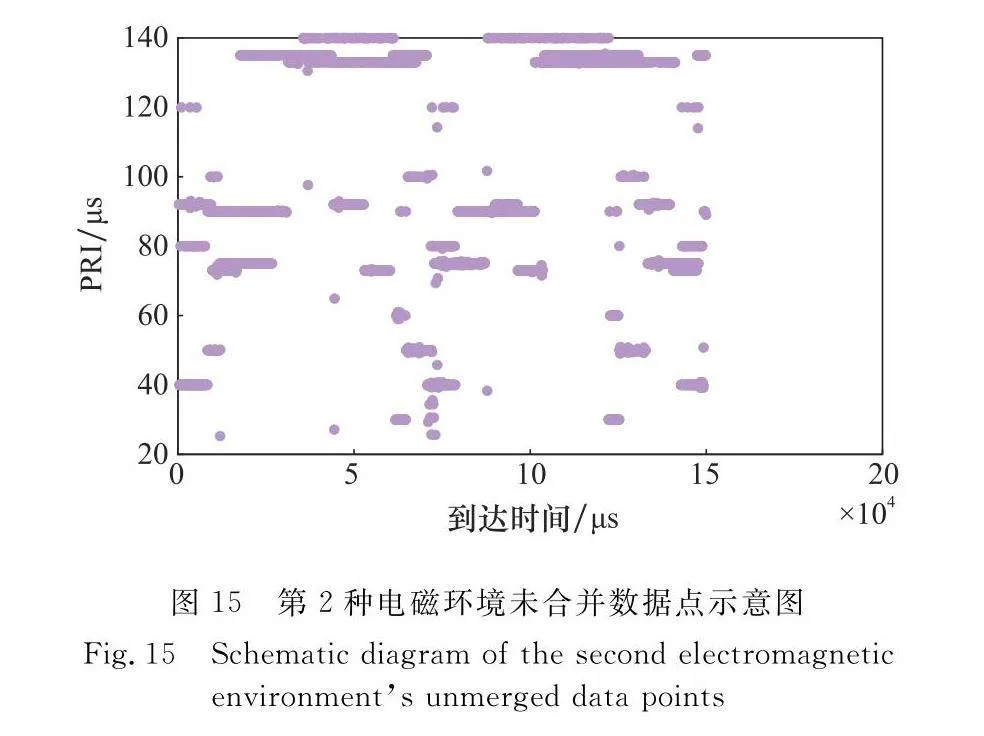
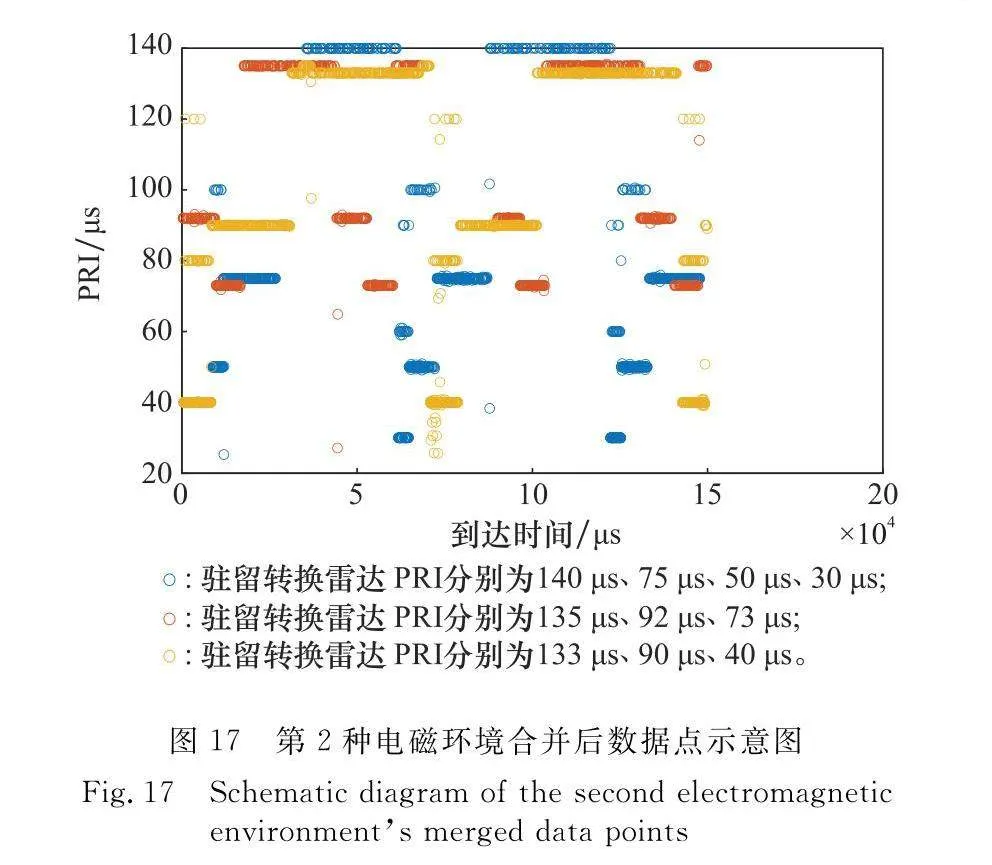
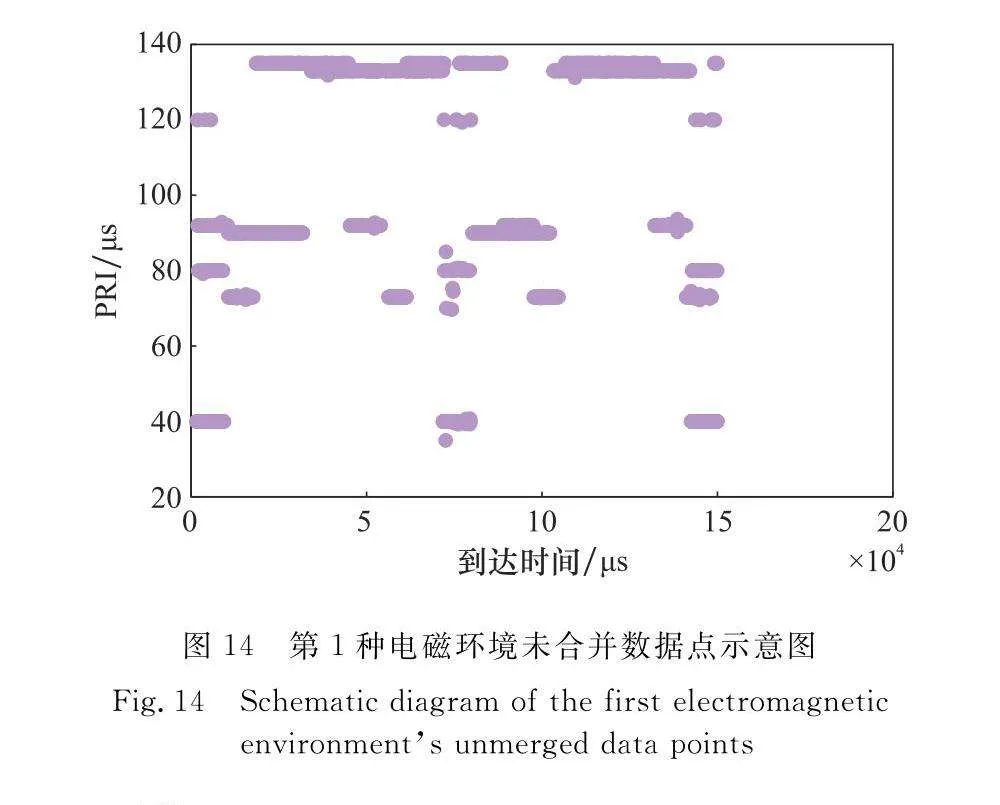
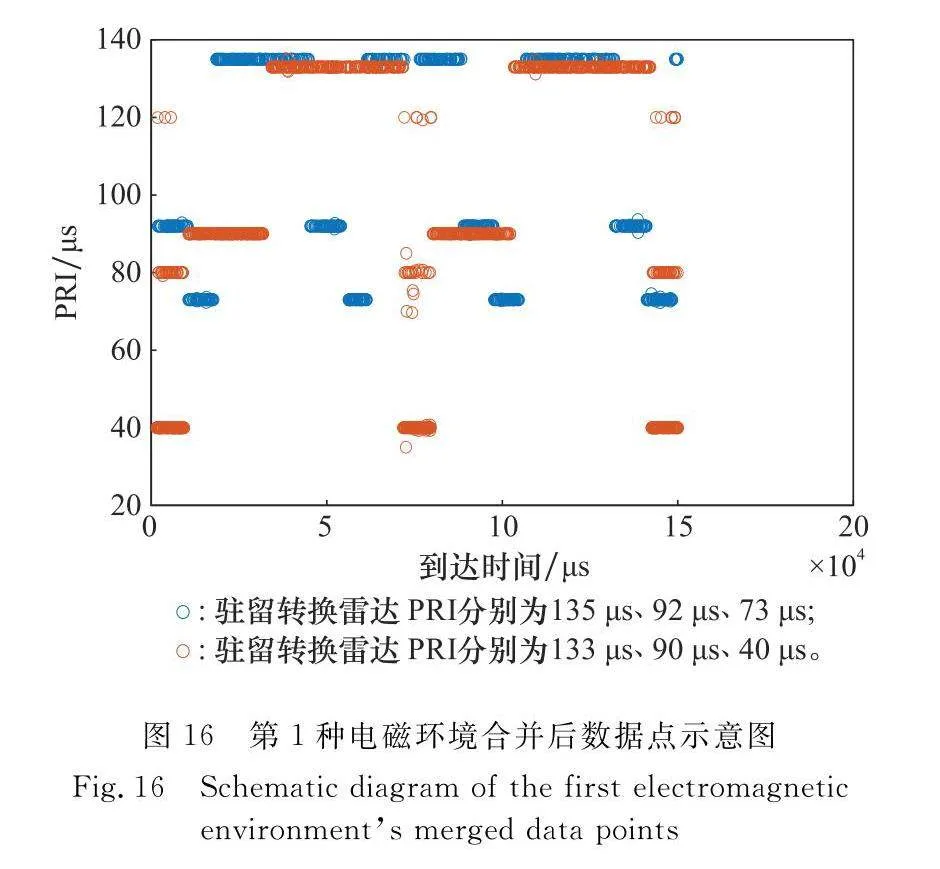
為驗證子周期合并具體效果，仍選擇第3.3節中的兩種復雜電磁環境，針對第3.3節中兩種電磁環境所搜索提取到的脈沖數據點集合進行合并，兩種電磁環境未合并前雜亂無章的數據點分別如圖14和圖15所示，而合并后完成分類的數據點分別如圖16和圖17所示。

如圖16和圖17所示，合并效果明顯，合并結果完成正確，圖16在90 μs與92 μs以及133 μs與135 μs等嚴重交疊情況下仍合并成功，而圖17則在更復雜的電磁環境下成功將3部駐留轉換雷達信號、共10個子周期成功合并。圖中部分數據點未處于其所屬PRI位置為脈沖丟失現象導致，是在復雜電磁環境中進行搜索的正常現象。通過本文算法，成功將子周期與其所屬的駐留轉換雷達信號一一對應，真正實現了針對駐留轉換雷達信號的分選。

4 結 論

本文提出一種針對駐留轉換雷達的信號分選算法。首先利用雙門限提高子周期PRI檢測概率，獲取特征，進行預處理，再通過霍夫變換結合迭代自組織聚類判斷信號是否屬于駐留轉換雷達信號，改進搜索算法，提取脈沖序列，依據排列熵指標將離群點處理后的多脈沖序列合并為1部駐留轉換雷達信號。仿真實驗結果表明，所提算法在復雜電磁環境下，PRI檢測概率高，識別駐留轉換類型準確，脈沖序列搜索提取正確，可以將駐留轉換雷達信號成功分選。

參考文獻

［1］CHEN C X， HE M H， XU J， et al. A new method for sorting unknown radar emitter signal［J］. Chinese Journal of Electronics， 2014， 23（3）： 499-502.

［2］JIA J W， LIU L M， HAN Z Z. Research on anti-sorting signal design technology based on precise combination of stagger signal PRI［C］∥Proc.of the 4th International Conference on Power， Intelligent Computing and Systems， 2022.

［3］NAN H， PENG S R， YU J A， et al. Pulse interference method against PRI sorting［J］. The Journal of Engineering， 2019， 2019（19）： 5732-5735.

［4］AHMED M G S， TANG B. Sorting radar signal from symmetry clustering perspective［J］. Journal of Systems Engineering and Electronics， 2017， 28（4）： 690-696.

［5］JIANG W， FU X J， CHANG J Y. Improved deinterleaving algorithm of radar pulses based on dual fuzzy vigilance ART［J］. Journal of Systems Engineering and Electronics， 2020， 31（2）： 303-311.

［6］LIU Y C， ZHANG Q Y. Improved method for deinterleaving radar signals and estimating PRI values［J］. IET Radar， Sonar amp; Navigation， 2018， 12（5）： 506-514.

［7］ZHANG C J， LIU Y C， SI W J. Synthetic algorithm for deinterleaving radar signals in a complex environment［J］. IET Radar， Sonar amp; Navigation， 2020， 14（12）： 1918-1928.

［8］MARDIA H K. New techniques for the deinterleaving of repetitive sequences［J］. IEE Proceedings F （Radar and Signal Processing）， 1989， 136（4）： 149-154.

［9］MILOJEVIC D J， POPOVIC B M. Improved algorithm for the deinterleaving of radar pulses［J］. IEE Proceedings F （Radar and Signal Processing）， 1992， 139（1）： 98-104.

［10］MAO Y， GUO G H， HAN J， et al. An improved algorithm of PRI transform［C］∥Proc.of the Global Congress on Intelligent Systems， 2009： 145-149.

［11］BAGHERI M， SEDAAGHI M H. A new approach to pulse deinterleaving based on adaptive thresholding［J］. Turkish Journal of Electrical Engineering amp; Computer Sciences， 2017， 25（5）： 3827-3838.

［12］ZHANG C J， LIU Y C， SI W J. Synthetic algorithm for deinterleaving radar signals in a complex environment［J］. IET Radar， Sonar amp; Navigation， 2020， 14（12）： 1918-1928.

［13］WANG C， SUN L T， LIU Z M， et al. A radar signal deinterleaving method based on semantic segmentation with neural network［J］. IEEE Trans.on Signal Processing， 2022， 70： 5806-5821.

［14］LIU Y F， XIE J， TAO M L， et al. Stagger PRI radar signal deinterleaving based on image semantic segmentation［C］∥Proc.of the 5th International Conference on Electronic Information and Communication Technology， 2022.

［15］張春杰， 劉俞辰， 司偉建. 基于多級箱與深度森林的雷達信號分選算法［J］. 電子學報， 2022， 50（6）： 1351-1358.

ZHANG C J， LIU Y C， SI W J. The radar signal deinterlea-ving algorithm based on multi-level bin and deep forest［J］. Acta Electronica Sinica， 2022， 50（6）： 1351-1358.

［16］QU Q Z， WEI S J， WU Y， et al. ACSE networks and autocorrelation features for PRI modulation recognition［J］. IEEE Communications Letters， 2020， 24（8）： 1729-1733.

［17］NGUYEN P， NGUYEN H Q. Classification of pulse repetition interval modulations using neural networks［C］∥Proc.of the IEEE Symposium Series on Computational Intelligence， 2018.

［18］AHMED U I， REHMAN T U， BAQAR S， et al. Robust pulse repetition interval （PRI） classification scheme under complex multi emitter scenario［C］∥Proc.of the 22nd International Microwave and Radar Conference， 2018.

［19］LI X Q， LIU Z M， HUANG Z T. Attention-based radar PRI modulation recognition with recurrent neural networks［J］. IEEE Access， 2020， 8： 57426-57436.

［20］LIANG Y S， CHEN Y G， SHEN B Y. Heuristic approach for PRI modulation recognition based on symbolic radar pulse trains analysis［C］∥Proc.of the Eurasia Conference on IOT， Communication and Engineering， 2022.

［21］HAN J W， PARK C H. A unified method for deinterleaving and PRI modulation recognition of radar pulses based on deep neural networks［J］. IEEE Access， 2021， 9： 89360-89375.

［22］陳濤， 王天航， 郭立民. 基于PRI變換的雷達脈沖序列搜索方法［J］. 系統工程與電子技術， 2017， 39（6）： 1261-1267.

CHEN T， WANG T H， GUO L M. Sequence searching methods of radar signal pulses based on PRI transform algorithm［J］. Systems Engineering and Electronics， 2017， 39（6）： 1261-1267.

［23］馬爽， 王瑩桂， 柳征， 等. 基于序列比對的多功能雷達搜索規律識別方法［J］. 電子學報， 2012， 40（7）： 1434-1439.

MA S， WANG Y G， LIU Z， et al. A method for search schema recognition of multifunction radars based on sequence alignment［J］. Acta Electronica Sinica， 2012， 40（7）： 1434-1439.

［24］CHENG W H， ZHANG Q Y， DONG J M， et al. An enhanced algorithm for deinterleaving mixed radar signals［J］. IEEE Trans.on Aerospace and Electronic Systems， 2021， 57（6）： 3927-3940.

［25］DADGARNIA A， SADEGHI M T. A novel method of deinterleaving radar pulse sequences based on a modified DBSCAN algorithm［J］. China Communications， 2023， 20（2）： 198-215.

［26］MA J T， YU J P， LIANG G， et al. Maneuvering target coherent integration and detection in PRI-staggered radar systems［J］. IEEE Geoscience and Remote Sensing Letters， 2022， 19： 3508205.

［27］LONG X W， LI K， TIAN J， et al. Ambiguity function analysis of random frequency and PRI agile signals［J］. IEEE Trans.on Aerospace and Electronic Systems， 2021， 57（1）： 382-396.

［28］NUHOGLU M A， ALP Y K， ULUSOY M E C， et al. Image segmentation for radar signal deinterleaving using deep learning［J］. IEEE Trans.on Aerospace and Electronic Systems， 2023， 59（1）： 541-554.

［29］GUO J C， HE Q B， ZHEN D， et al. Intelligent fault detection for rotating machinery using cyclic morphological modulation spectrum and hierarchical teager permutation entropy［J］. IEEE Trans.on Industrial Informatics， 2023， 19（4）： 6196-6207.

［30］LIN M Y， XIE H N， SHAN M Y. A hybrid multiscale permutation entropy-based fault diagnosis and inconsistency evaluation approach for lithium battery of E-vehicles［J］. IEEE Access， 2022， 10： 104757-104768.

［31］高浩瀚， 張利， 梁軍， 等. 基于改進排列熵算法和Yamamoto算法的非侵入式用電設備狀態變化檢測［J］. 電力自動化設備， 2020， 40（1）： 192-197.

GAO H H， ZHANG L， LIANG J， et al. Non-intrusive electrical equipment state change detection based on improved permutation entropy algorithm and Yamamoto algorithm［J］. Electric Power Automation Equipment， 2020， 40（1）： 192-197.

［32］張展， 劉亞晨， 杜詩揚， 等. 基于CEEMD與排列熵相結合的諧波檢測方法研究［J］. 電子測量技術， 2022， 45（9）： 92-98.

ZHANG Z， LIU Y C， DU S Y， et al. Harmonic detection method based on CEEMD and permutation entropy［J］. Electronic Measurement Technology， 2022， 45（9）： 92-98.

作者簡介

張春杰（1975—），女，副教授，博士，主要研究方向為被動雷達信號處理。

青 松（1995—），男，碩士研究生，主要研究方向為被動雷達信號分選。

鄧志安（1985—），男，副教授，博士，主要研究方向為陣列信號處理、寬帶信號處理。

劉俞辰（1997—），男，助理工程師，碩士，主要研究方向為被動雷達信號分選。