基于動態成本卷積的復雜產品批產路徑優化問題建模與求解研究




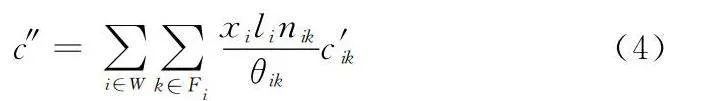
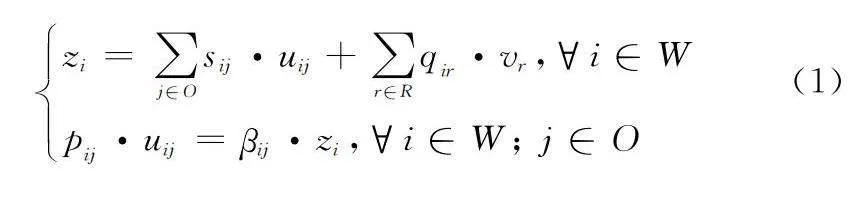





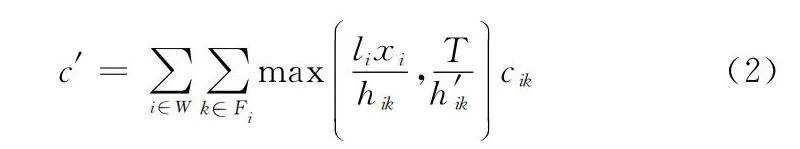
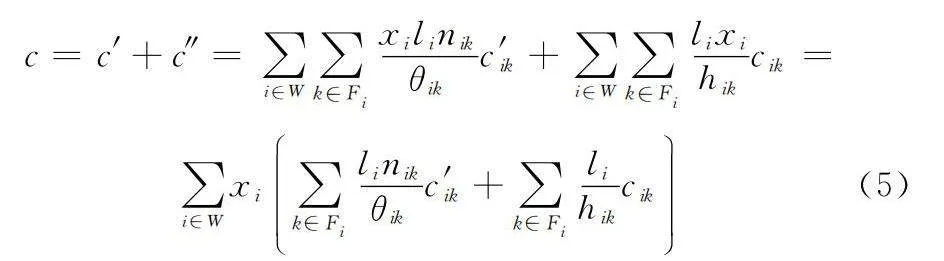

摘要: 具有復雜工藝路線的裝備產品,其生產系統設計的待決策變量之間通常相互耦合、相互影響,對產品最終的批產成本產生著影響,構成了較為復雜的組合優化問題。對此,提出一種基于動態成本卷積的復雜產品批產路徑優化模型。該模型考慮了復雜產品工藝路線的各節點均可能存在多種生產設計選項,在各選項對應著不同生產投入和批量效率的情況下,以最終交付產品的批產成本最小化為目標輸出生產系統設計和成本卷積路徑。同時,建立了混合整數規劃模型,并通過對模型中非線性成分實施可控精度線性化,將模型換化為可最優求解的線性模型。最后,針對某連續生產行業設計了小、中、大規模實驗算例,驗證了所提模型的可行性、合理性和求解效率。
關鍵詞: 批產成本; 成本卷積; 路徑優化; 優化模型
中圖分類號: C 94
文獻標志碼: A
DOI:10.12305/j.issn.1001-506X.2024.06.19
Research on modeling and solution of complex product batch production routing optimization based on dynamic cost convolution
YANG Liying1, YANG Ruiyi2, CUI Xinhao2, ZHANG Siyue2, CHEN Lian3, XIAO Yiyong2,*
(1. National Key Laboratory of Particle Transport and Separation Technology, Research Institute of Physical and Chemical Engineering of Nuclear Industry, Tianjin 300180, China;
2. School of Reliability and Systems Engineering, Beihang University, Beijing 100191, China;
3. The 714 Research Institute of China State Shipbuilding Corporation Limited, Beijing 100101, China)
Abstract: Equipment products with complex process routes often have decision variables in their production system design that are coupled and affect with each other, affecting the final batch production cost of the product and forming a complex combinatorial optimization problem. In this regard, a complex product batch production routing optimization model based on dynamic cost convolution is proposed. The proposed model considers that there may be multiple production design options at each node of the complex product process routing, and each option corresponds to different production inputs and batch efficiency. The goal is to minimize the batch production cost of the final delivered product and output the production system design and cost convolution routing. At the same time, a mixed integer programming model is established, and by implementing controllable precision linearization on the nonlinear components in the model, the model is transformed into a linear model that can be optimally solved. Finally, small, medium, and large-scale experimental examples are designed for a certain continuous production industry to verify the feasibility, rationality, and solution efficiency of the proposed model.
Keywords: batch production cost; cost convolution; routing optimization; optimization model
0 引 言
生產系統優化設計是生產運作管理領域的重要研究內容,圍繞生產效率、產品質量、交付時間和降低成本等多方面的評價目標,長期以來在工業界和學術界開展著廣泛的理論研究和應用實踐。在裝備研制與生產領域,生產成本是產品壽命周期費用的重要組成部分,也是產品經濟性設計的重要內容。當某新研產品完成設計定型進入批產階段后,批產成本就成為生產系統設計的一項重要優化目標,也是評價生產系統優劣性的重要指標。
產品的批產成本受到諸多因素的影響,例如生產批量計劃、供應鏈管理、生產設施選址、生產設備選型、車間布局優化、設備維修保障策略,以及生產工藝流程設計等。如何集成這些因素進行綜合優化設計,以最大程度地降低產品批產成本,已經成為生產系統優化設計的主要內容。不同行業產品的批產成本影響因素通常具有較大的差異性,因此通過研究生產系統的特點,進而有針對性地開展生產系統優化設計,已成為當前批產成本優化的一個研究熱點方向。
多級經濟批量問題是生產批量優化方面的典型問題[1]。該問題以批產成本為優化目標,研究核心企業與多級供應商之間進行集成優化的生產經濟批量模型及求解算法[2]。文獻[3]研究了帶約束的經濟批量問題及動態規劃算法。文獻[4-5]研究了經濟批量與學習效應之間的影響關系。文獻[6]研究了單元生產中研制訂單和批產訂單的混合調度問題,考慮了隨機事件的動態調度算法。文獻[7]從降本增效、提升產業化能力方面對武器平臺電子產品的批量化生產過程進行探討。文獻[8]研究了針對制造業生產車間多品種、多階段生產問題的生產邏輯模型和優化方案。文獻[9]對相關的數學模型進行了系統性綜述。
生產線優化設計也是現有文獻研究批產成本優化的一個重要方面。文獻[10]研究了面向生產快速反應、高效作業和低成本綜合目標的復雜電子產品柔性生產線建設的優化問題。文獻[11]研究了批產制造項目的進度管理,采用啟發式算法基于資源重新分配優化了關鍵生產鏈問題。文獻[12]研究了低成本批產商業通信衛星的任務特點和設計要求,提出了面向批生產低成本衛星的元器件保障模式。在生產線流程優化方面,日本的單元式生產被認為是傳統福特流水生產線模式的一種新的替代,在降低生產成本和提升生產效率方面有顯著優勢[13-15]。
文獻[16]研究了生產設施布局問題以及動態設施布局問題[17],提出了在考慮外部需求變化的情況下,如何動態調整生產設施布局與工藝路線流程,以降低產品批產成本為目標建立優化模型。文獻[18]研究了工廠設施的連續選址問題,以降低運輸成本為優化目標,為之建立了混合整數規劃模型。文獻[19]研究了面向利潤最大化的批量生產計劃的非陣列排序優化模型。文獻[20]研究了考慮產能擴張的生產組合計劃優化問題。
對于串行生產系統,由設備故障引發的生產系統暫停對生產效率有較大影響,因此設備維修策略是生產系統設計的重要內容[21-22]。其中,文獻[21]提出了帶緩沖區的串行生產系統預防性維護決策優化模型及啟發式求解算法,文獻[22]提出了一種面向串聯生產系統設備維護的考慮在線決策與緩沖分配的聯合優化模型。文獻[23]提出了設備狀態與預防性維護周期相結合的預防維護策略,以單位時間總質量成本最小化為目標建立優化模型。相關的綜述可參考文獻[23],該文獻分析了生產系統中設備維修管理、統計過程控制及經濟生產批量決策的相互影響和作用機制,對相關應用問題研究現狀進行了梳理和分析。
復雜產品批產成本優化領域還有一個被稱之為組裝路徑優化問題(assembly routing problem, ARP)的經典問題[24-26]。ARP考慮了在復雜產品具有多層零件結構、每種零件有多個供應商、每個供應商有多個供應地點/倉庫的場景下,如何優化物流供應路徑,在滿足多周期客戶交付要求的前提下實現生產成本最小化。當ARP向后延伸到考慮多客戶的交貨地點和緩存倉庫并考慮終端產品運輸路徑而優化生產批量時,就轉化為另一種形式的生產路徑優化問題(production routing problem, PRP)[27-30]、倉儲路徑優化問題(inventory routing problem, IRP)[31],以及生產與分運集成調度(integrated production and distribution scheduling, IPDS)問題[32-33]。
現有文獻中還包括有較多的針對具體行業的生產系統優化案例研究,包括制氫行業的生產路徑優化問題[34],以及從成本、碳排放和風險等角度建立的制氫供應鏈多目標優化模型[35]和相關綜述文獻(文獻[36])。文獻[37]研究了農業生物行業的供應鏈優化模型。文獻[38]從生產規模、集成度、運輸和供應鏈配置等方面,研究了生物燃料生產行業的成本優化問題。文獻[39]從產量、成本、能源等7個角度,研究了食品供應鏈的多目標優化模型。
上述文獻關于批產成本優化的研究主要集中針對典型問題模型的局部區域,如生產經濟批量、工序優化、設施布局等。關于如何從生產系統整體設計角度優化產品批產成本的相關理論模型研究還比較少,還缺乏面向復雜產品全生產過程和生產系統批產成本的優化模型。對生產線的優化研究目前還主要針對單一生產線,較少有針對多生產線耦合而組成的復雜生產系統的優化研究。
本文根據實際工程需要,提煉出了面向生產系統整體優化的批產成本優化問題,建立了一種基于動態成本卷積的產品批產路徑優化模型。該模型考慮了產品批產過程中的重復性直接投入成本和生產系統維修消耗,以及非重復性的成本投入,如研發投入、生產線建設等各種一般性的成本要素,為具有復雜生產工藝路線的產品批產提供最優化的成本卷積路徑。所提出的優化模型采用了線性化設計技術,可應用商業求解器(如Cplex,Gurobi等)進行直接求解。對某連續生產行業的模擬算例表明,對于中小規模問題,該模型可在1 h計算時間內獲得最優解。對于大規模問題,可在可接受時間內獲得次優可行解。
1 基于制程的成本動態卷積模型
1.1 直接生產成本
生產制程即生產制造過程,是指通過使用和消耗生產資源,如人工、設備、能源、輔料、外部產品或服務等,將輸入原材料或半成品轉換為輸出產品的一組有序過程,也稱為生產線,例如:半導體生產過程、精密件加工過程、成品組裝過程,以及專有生產服務支持(如特種搬運、激光調制)等。圖1描繪了一個輸出某種產品或服務的生產制程概念模型。
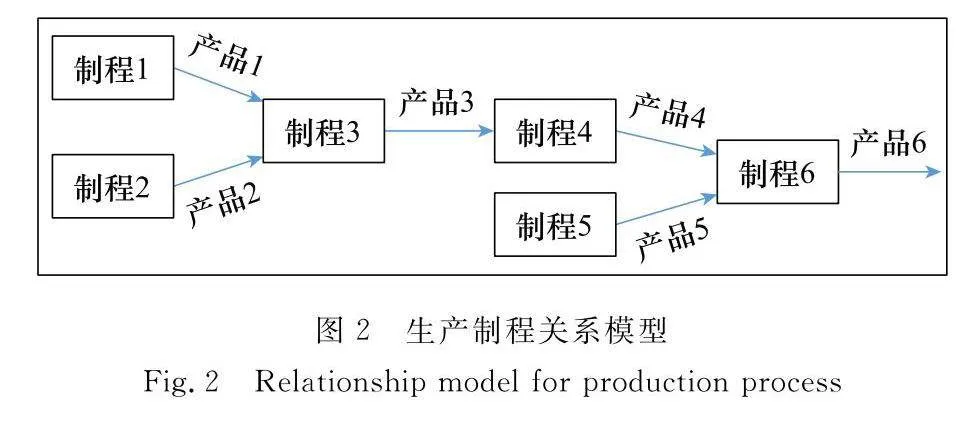
生產系統往往包含多條生產制程,共同組成網狀結構的生產制程關系模型,如圖2所示。其中,制程3分別領用制程1和制程2的產品1和產品2,輸出產品3,然后被制程4領用,輸出產品4,再與生產制程5輸出的產品5一起被生產制程6領用,最后輸出終端產品6。
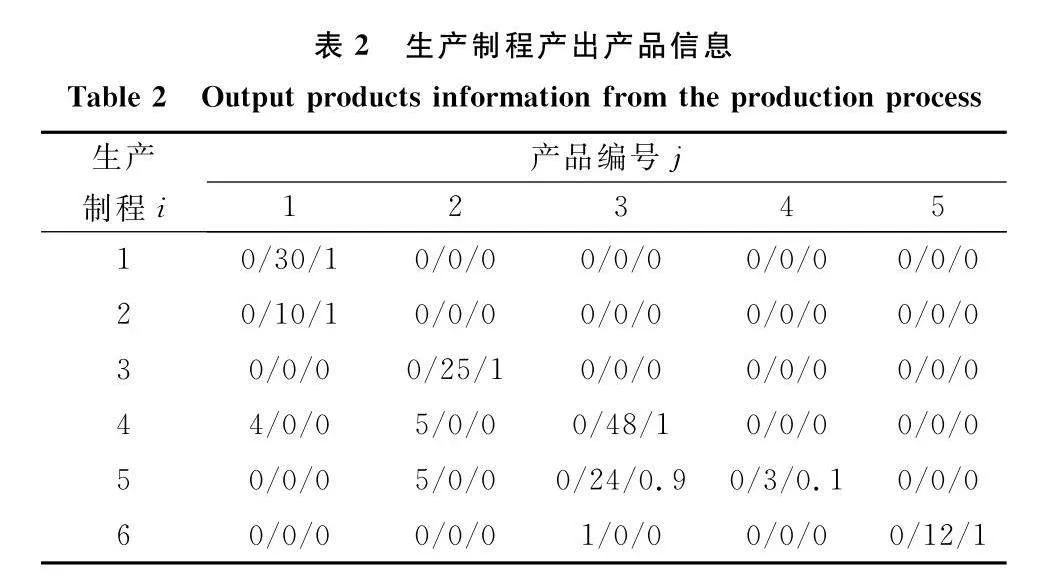
以W表示生產制程的集合,O表示生產制程輸出產品的集合,pij表示制程i輸出產品j的每批次產量,sij為制程i對產品j的每批次用量,βij為生產制程i的產出產品j所占成本比例,其中i∈W, j∈O。以R表示制造資源集合,如人工、設備、外購材料、能源等,qir表示生產制程i對制造資源r的每批次消耗量,vr表示制造資源r的成本單價,其中i∈W, r∈R。以uij表示生產制程i生產產品j的單位成本,zi表示生產制程i的單批次成本,那么,對每一個生產制程i,有如下成本卷積表達式:
zi=∑j∈Osij·uij+∑r∈Rqir·vr,?i∈W
pij·uij=βij·zi,?i∈W; j∈O(1)
1.2 生產設備維修成本
(1) 預防性維修費用
預防性維修是為了確保生產制程系統保持設計功能和性能,以及防止故障發生而采取的周期性檢查、潤滑、備件更換等措施,例如各種小修、定檢、中修、大修等。預防性維修活動產生的費用稱為預防性維修費用。預防性維修是計劃性的,其費用可以進行預先估算。
預防性維修費用分析如下:令W表示生產系統的生產制程集合;以Fi表示對生產制程i的預防性維修項目集合,li表示生產制程i的單批次生產時間,其中i∈W;以hik表示預防性維修項目的工作時間間隔,h′ik表示預防性維修項目的日歷時間間隔,其中i∈W, k∈Fi;以cik表示單次預防性維修活動的費用,其中i∈W, k∈Fi。在給定的計劃時間T內,對于生產制程i,若其生產批次數為xi,那么所產生的預防性維修費用為
c′=∑i∈W∑k∈Fimaxlixihik,Th′ikcik(2)
式中:max函數表示按先到為主原則,取按日歷時間和按工作時間計算所得的大者為實際維修次數。通常認為日歷時間間隔h′ik遠大于工作時間間隔h′ik,或者設備被共享使用時,維修次數主要按工作時間計算。因此,第i生產制程的預防性維修費用估算式可簡寫為
c′=∑i∈W∑k∈Filixihikcik(3)
(2) 故障性維修費用
故障性維修是指生產系統發生故障后或者出現故障征兆等情況下進行的非計劃性維修。故障性維修活動產生的費用稱為故障性維修費用。故障性維修是非計劃性的,事先未必知道在什么時候要發生何種維修活動。但根據生產設備的可靠性指標以及故障模式分布規律,也可以估算出給定期間的故障性維修期望費用。故障性維修費用分析如下:以Gi表示生產制程的設備集合,以nik表示設備的安裝數量,其中i∈W, k∈Gi;以θik表示設備的可靠性指標平均故障間隔時間(mean time between failure,MTBF),i∈W, k∈Gi;以Eik表示設備的故障模式集合,以λikj表示故障模式的占比率,以c′ikj表示設備發生故障的修復費用。其中,i∈W, k∈Gi, j∈Eik。
c″=∑i∈W∑k∈Fixilinikθikc′ik(4)
綜上,生產系統維修費用可表示為
c=c′+c″=∑i∈W∑k∈Fixilinikθikc′ik+∑i∈W∑k∈Filixihikcik=
∑i∈Wxi∑k∈Filinikθikc′ik+∑k∈Filihikcik(5)
令ci表示生產制程i的一批次生產對應的平均生產系統維修成本,表示為
ci=∑k∈Filinikθikc′ik+∑k∈Filihikcik(6)
1.3 非重復性成本分攤
在生產成本中考慮非重復性投入成本,如產品前期研發費用、生產系統建設費用、技改費用等。以bi表示生產制程i的非重復性成本,按總生產批次數均攤入制程生產成本,即bi/xi。其中,xi是制程i的生產批次數。這樣,在納入非重復成本均攤和生產維修費用的情況下,式(1)成本卷積公式改寫為
zi=∑j∈Osij·uij+∑r∈Rqir·vr+ci+bi/xi,?i∈W
pij·uij=βij·zi, ?i∈W;j∈O(7)
2 基于動態成本卷積的批產路徑優化模型
2.1 符號定義
(1) 模型參數
W:生產制程集合,i∈W, i′∈W
O:自制產品(或服務)集合,j∈O
R:生產資源集合,如人工、設備、材料、能源等,r∈R
pij:制程i產出產品j的每批次產量
p′ij:0/1參數,表示制程i是否產出產品j
βij:制程i產出產品j的成本占比,即當產出多種產品時不同產品之間的成本占比,有∑j∈Oβij=1且βij≤p′ij,M為一個大數
qir:制程i每批次對生產資源r的消耗量
sij:制程i每生產批次領用產品j的數量
s′ij:0/1參數,表示制程i是否領用產品j
vr:生產資源r的成本單價
dj:產品j的外部需求量
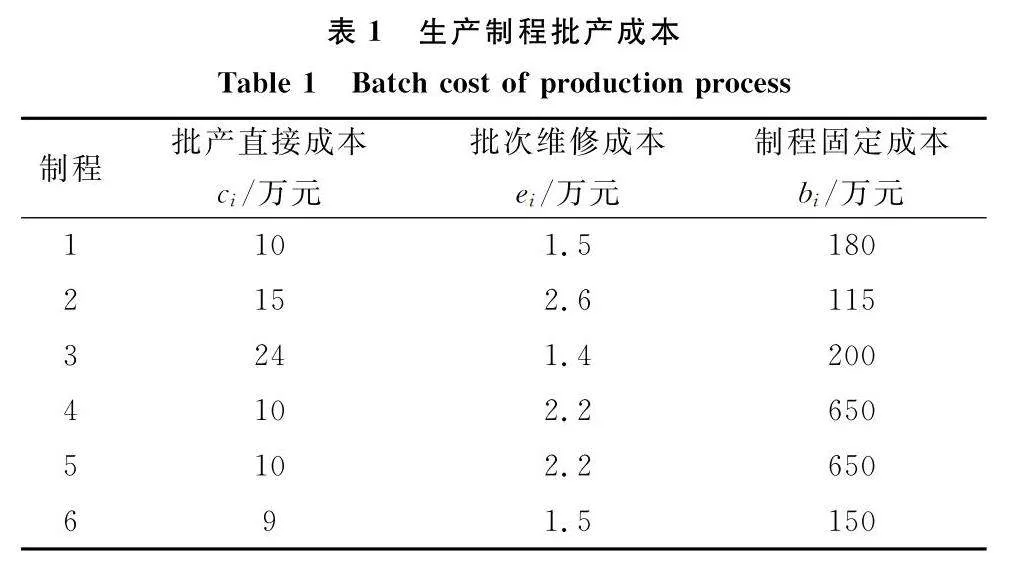
ci:制程i每批次設備維修費用,見式(6)
bi:制程的固定費用(非重復性投入的研發費、生產線建設費、技改費等)
M:一個大數
(2) 決策變量
x′i:0/1變量,表示制程i是否啟用
πii′j:0/1變量,表示成本卷積路徑,即制程i是否領用制程i′產出的產品j
θii′j:非負連續變量,表示卷積的成本值,即制程i領用制程i′產出產品j的成本
xi:非負整數變量,表示制程i的生產批次數
zi:非負連續變量,表示制程i的單批次成本
uij:非負連續變量,表示制程i產出產品j的每單位成本
2.2 數學規劃模型
(1)目標函數
min Total_Cost=∑i∈W∑j∈Odj·uij(8)
(2)約束條件
設定x與x′的關系:
x′i≤xi,?i∈W
xi≤Mx′i,?i∈W (9)
(10)
設定各制程的生產批次數剛好滿足需求:
∑i∈Wxipij≥∑i∈Wxisij+dj,?j∈O
∑i∈W(xi-1)pij≤∑i∈Wxisij+dj,?j∈O (11)
(12)
設定產品的成本卷積路徑:
πii′j≤s′ijp′ij(xi+x′i)/2,?i∈W;i′∈W;j∈O
∑i′∈Wπii′j≥s′ijx′i,?i∈W;j∈O (13)
(14)
優化產品的卷積成本:
θii′j≤Mπii′j, ?i∈W;i′∈W;j∈O
θii′j≥sijuij-M(1-πii′j), ?i∈W;i′∈W;j∈O
θii′j≤sijuij+M(1-πii′j), ?i∈W;i′∈W;j∈O
uij≤Mp′ijx′ij, ?i∈W;j∈O (15)
(16)
(17)
(18)
計算產品的批次成本:
zi≥∑i′∈W∑j∈Oθii′j+∑r∈Rqirvr+ci+bixi-
M(1-x′i),?i∈W
zi≤∑i′∈W∑j∈Oθii′j+∑r∈Rqirvr+ci+bixi+
M(1-x′i),?i∈W
(19)
(20)
計算產品的單位批產成本:
pijuij=βijzi,?i∈W;j∈O
zi≤Mx′i,?i∈W(21)
(22)
定義變量的值域:
xi為非負整數,zi≥0;uij≥0
πii′j,x′i∈{0,1};θii′j≥0,?i,i′∈W;j∈O(23)
上述模型中,目標函數為滿足外部需求的產品總成本最小化。約束式(9)和式(10)確定了變量xi和x′i之間的關系;約束式(11)和式(12)確保了生產制程之間的產品輸出量滿足需求量,以及同時滿足外部需求量,其中式(12)限定了產量批次上限;約束式(12)和式(13)確保了產品成本卷積路徑的合理性,其中式(13)確保了制程i能夠領用制程i′產出的產品j的條件是:s′ij=1且p′ij=1且xi+x′i=2,式(14)確保了產品領用路徑關系必須得到滿足;約束式(14)~式(18)基于成本卷積路徑變量πii′j確定了成本卷積的數量關系θii′j,其中式(14)設定了若不存在卷積路徑(πii′j=0),則成本卷積數量θii′必須為0,式(15)和式(16)用大數條件約束法設定了當πii′j=0時,θii′必須取值sijuij,即領用的產品數量乘以產品的單位成本,式(17)設定了當制程i不產出產品j(即p′ij=0)或生產制程i未啟用(即x′i=0)時,制程i產出的產品j的單位成本為0(即uij=0);約束式(19)和式(20)設定了制程i的單批次成本zi的計算方法,即“所領用的其他制程產出產品的成本+本制程的生產資源消耗成本+所產生的生產設備維修成本ci+固定費用的分攤成本Bi/xi”,且以大數條件約束法確保了該約束式僅當x′i=1時有效;約束式(21)和式(22)表示當制程i產出多種產品時,產品之間的成本分攤比例按照給定占比βij分攤,式(22)表示當制程i未啟用時,zi為0;約束式(23)定義了變量的值域。
2.3 模型求解
上述模型中,約束式(19)和式(20)中存在非線性成分,即Bi/xi。下面利用割線法將該非線性成分進行線性化近似化。對一般性的曲線方程 y=1/x,割線法線性化是指以一組割線y=Klx+Bl(l=1,2,…,η)將曲線 y=1/x代替為線性化方法:
y≥Klx+Bl,?l=1,2,…,η(24)
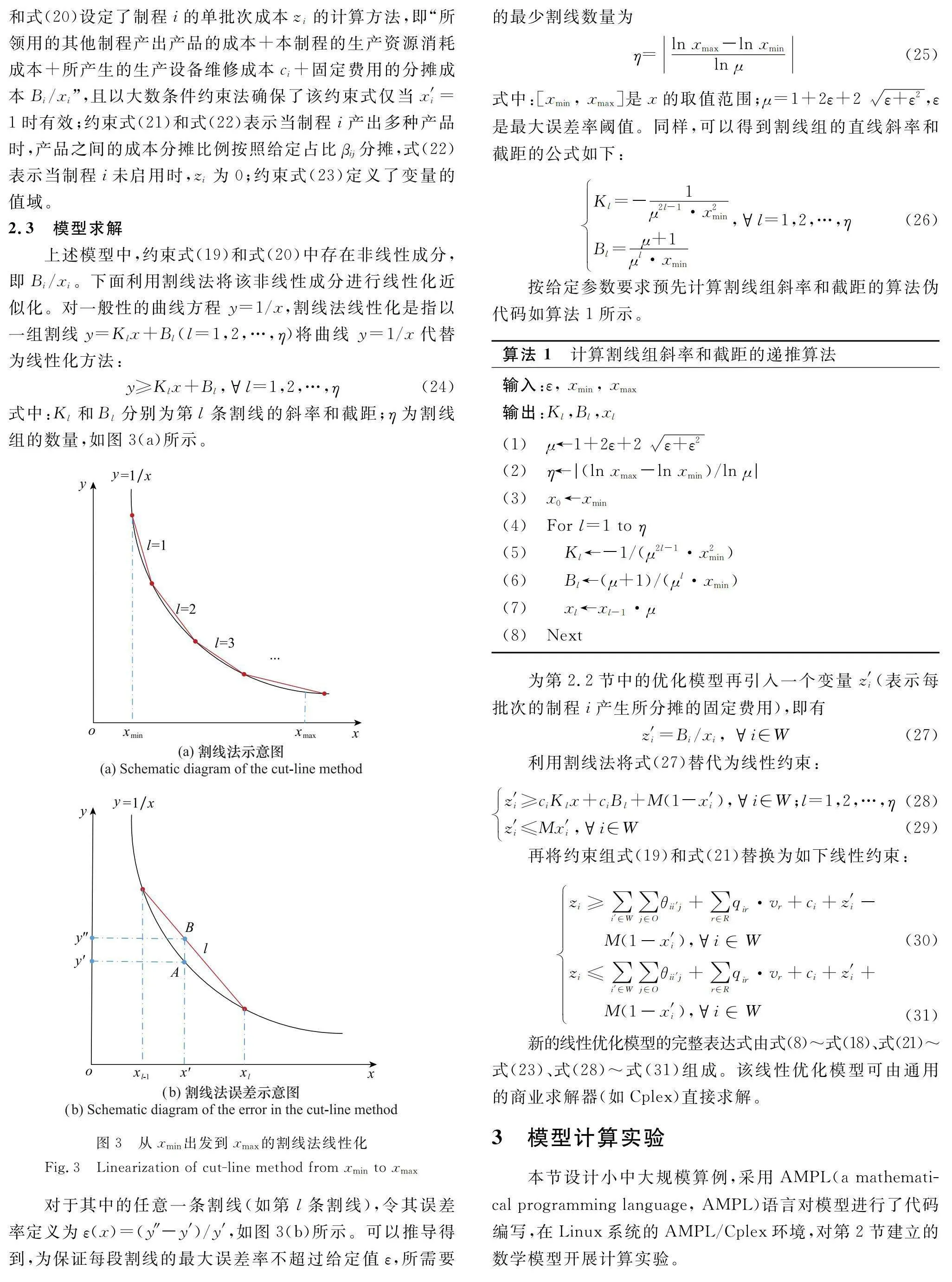
式中:Kl和Bl分別為第l條割線的斜率和截距;η為割線組的數量,如圖3(a)所示。
對于其中的任意一條割線(如第l條割線),令其誤差率定義為ε(x)=(y″-y′)/y′,如圖3(b)所示。可以推導得到,為保證每段割線的最大誤差率不超過給定值ε,所需要的最少割線數量為
η=ln xmax-ln xminln μ(25)
式中:[xmin, xmax]是x的取值范圍;μ=1+2ε+2ε+ε2,ε是最大誤差率閾值。同樣,可以得到割線組的直線斜率和截距的公式如下:
Kl=-1μ2l-1·x2min
Bl=μ+1μl·xmin,?l=1,2,…,η(26)
按給定參數要求預先計算割線組斜率和截距的算法偽代碼如算法1所示。
新的線性優化模型的完整表達式由式(8)~式(18)、式(21)~式(23)、式(28)~式(31)組成。該線性優化模型可由通用的商業求解器(如Cplex)直接求解。
3 模型計算實驗
本節設計小中大規模算例,采用AMPL(a mathematical programming language, AMPL)語言對模型進行了代碼編寫,在Linux系統的AMPL/Cplex環境,對第2節建立的數學模型開展計算實驗。
3.1 小規模實證算例
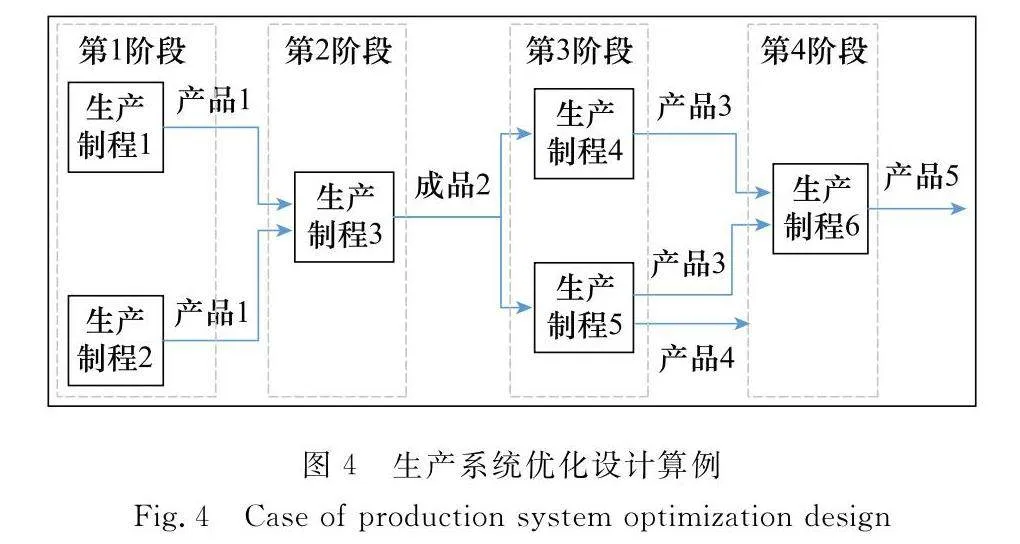
某企業研發出了某產品的新型材料生產工藝,并進入了新生產系統優化設計階段。如圖4所示,該產品需要經歷4個主要生產階段,形成3種中間產品(產品1、產品2和產品3)以及最終產品——產品5。其中,第1階段產出中間產品“產品1”,第2階段領用“產品1”再加工后產出中間產品“產品2”,第3階段領用“產品2”再加工輸出中間產品“產品3”,第4階段領用“產品3”再加工輸出中間產品“產品4”。為了優化生產成本,為第1階段設計了2種生產方案,即生產制程1和生產制程2,為第3階段也設計了2種生產方案,即生產制程4和生產制程5。其中,生產制程5除了產出“產品3”外,還產出“產品4”(為副產品)。同一種產品的不同生產方案對應著不同的投資成本、生產效率/能力、資源消耗和設備使用情況等。
圖4中的小規模算例不失一般性地展示了在生產系統設計階段存在多種候選生產方案的情況下,如何根據生產方案的特點進行批產成本卷積路徑優化,在滿足產品交付要求的前提下實現批產成本優化的一般性問題。
將第2.2節中的優化模型用AMPL代碼實現,建立模型文件ProdCost.mod,如算法2所示。
算法 2 定義模型ProdCost.mod輸入: W,O,R,Nkb,p,p1,beta,q,s,s1,v,d,c,e,K,B,b,M
輸出: Total_Cost
#文件名ProdCost.mod
set W;
#生產制程集合
set O;
#產品(或服務)集合
set R;
#生產資源集合
param p{W,O};
#制程i是否產出產品j的批次產量
param p1{W,O};
#制程i是否產出產品j
param beta{W,O};
#制程i輸出產品的成本占比
param q{W,R};
#制程i對資源r的每批次消耗量
param s{W,O};
#制程i對產品j的批次用量
param s1{W,O};
#制程i對產品j是否具有領用關系
param v{R};
#生產資源r的成本單價param d{O};
#產品j的外部需求量
param c{W};
#制程i的生產資源費用
param e{W};
#制程i的維修費用
set Nkb;
#線性化的割線集合
param K{Nkb};
#割線的斜率
param B{Nkb};
#割線的截距
param b{W};
#生產制程i的固定費用
param M:=99999;
#一個大數
var x1{W} binary;
#0/1變量
var x{W}gt;=0 integer; #非負整數變量
var z{W}gt;=0;
#非負變量
var z1{W}gt;=0;
#非負變量
var u{W,O}gt;=0;
#非負變量
var pi{W,W,O} binary;
#0/1變量
var cita{W,W,O}gt;=0;
#非負變量
minimize Total_Cost: sum{i in W, j in O}(d[j]*u[i,j]);
subject to Con1a{i in W}: x1[i]lt;=x[i];
subject to Con1b{i in W}: M*x1[i]gt;=x[i];
subject to Con2a{j in O}:
sum{i in W}x[i]*p[i,j]gt;=sum{i in W}x[i]*s[i,j]+
d[j];
subject to Con2b{j in O}:
sum{i in W}(x[i]-1)*p[i,j]lt;=sum{i in W}x[i]*s[i,j]+d[j];
subject to Con3a{i in W, i1 in W, j in O}:
pi[i,i1,j]lt;=0.5*s1[i,j]*p1[i1,j]*(x1[i1]+x1[i]);
subject to Con3b{i in W, j in O}:
sum{i1 in W}pi[i,i1,j]gt;=s1[i,j]*x1[i];
subject to Con4a{i in W, i1 in W, j in O}:
cita[i,i1,j]lt;=M*pi[i,i1,j];
subject to Con4b{i in W, i1 in W, j in O: ilt;gt;i1}:
cita[i,i1,j]gt;=s[i,j]*u[i1,j]-M*(1-pi[i,i1,j]);
subject to Con4c{i in W, i1 in W, j in O: ilt;gt;i1}:
cita[i,i1,j]lt;=s[i,j]*u[i1,j]+M*(1-pi[i,i1,j]);
subject to Con4d{i in W, j in O}:
u[i,j]lt;=M*x1[i]*p1[i,j];
subject to Con5a{i in W}:
z[i]gt;=sum{i1 in W, j in O}cita[i,i1,j]+c[i]+e[i]+z1[i]-M*(1-x1[i]);
subject to Con5b{i in W}:
z[i]lt;=sum{i1 in W, j in O}cita[i,i1,j]+c[i]+e[i]+z1[i]+M*(1-x1[i]);
subject to Con5d{i in W}:
z[i]lt;=M*x1[i];
subject to Con6{i in W, j in O}:
p[i,j]*u[i,j]=beta[i,j]*z[i];
subject to Con7a{i in W, k in Nkb}: z1[i]gt;=b[i]*K[k]*x[i]+b[i]*B[k]-M*(1-x1[i]);
subject to Con7b{i in W}:
z1[i]lt;=M*x1[i];
令算法2輸入中各生產制程的批產成本數據如表1所示,生產制程與產品之間的領用數量、產出數量和成本占比如表2所示,并令產品3和產品5的外部需求量分別為110和120,其他產品的外部需求量為0。這樣,準備AMPL優化模型所需數據文件Instance4x2.dat,內容如算法3所示。
編寫AMPL執行腳本程序,調研Cplex求解算例及輸出,如表3所示。通過觀測數據可知,生產“產品1”啟用了生產制程2,而生產“產品3”啟用了生產制程4,獲得最低交付成本(目標函數)為806.525。對生產制程基本數據進行調整后重新計算,可以獲得與之相應的最優結果,表明模型達到了設計的預期效果。
3.2 大規模求解實驗
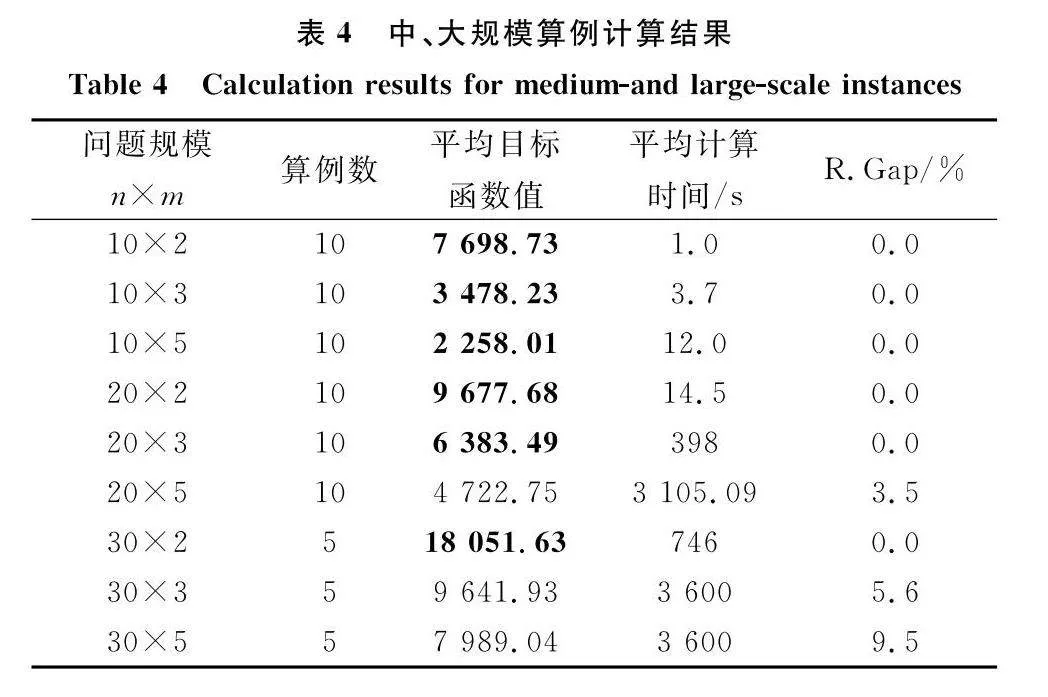
下面通過隨機構造中、大規模算例驗證所提出模型的求解效率。構造較復雜的生產系統,令產品生產過程包含n個生產階段,對應n個中間產品,每個中間產品設計有m個不同的候選生產制程方案,問題規模為n與m的組合,表示為 n×m。設置計算時間上限為3 600 s。表4給出了計算結果,其中黑體數據為最優值,R.Gap表示計算終止時,當前最好解(上界)與最大松弛解(下界)之間的相對差距值。可見,問題組10×2、10×3、10×5、20×2、20×3和30×2的問題都獲得了最優解。對于問題組20×5、30×3和30×5,本次計算在給定的時間(3 600 s)內未能獲得最優解,僅獲得了當前的最好上界值為問題的近似優化解。這表明增大問題規模參數n和m都對求解效率有顯著的正相關影響。計算結果表明,所提出的優化模型具有較高的求解效率,可在可接受時間內求解具有10至20個生產制程的中規模產品批產成本卷積路徑優化問題,且獲得了最優解(因為R.Gap值為0)。對于具有30個生產制程的大規模優化問題,則需要較長求解計算時間。
4 結束語
本文分析了產品規模生產階段的主要重復性生產成本和非重復成本,提出了產品批產成本卷積路徑優化的基本問題,給出了該問題的一種混合整數規劃線性模型。該模型可支持復雜產品的工藝路線優化設計,在多種復雜的、可行的工藝路線方案中,選擇出最優的批產成本卷積路徑,對于降低產品批產成本有決策支撐作用。所提出的優化模型可應用于商業求解軟件直接求解,對于生產制程規模在10~20之間的中規模算例,可以在較短的計算時間(10 min)內獲得最優解。對于超過30個生產制程的大規模問題,可在較長計算時間(約1 h)內獲得最優解或接近最優解。該問題的未來研究方向有兩點:① 對于更大規模算例的快速求解問題,可設計相應的求解效率更高的啟發式算法,以獲取給定時間內的可接受次優解;② 結合不同行業的工業應用,考慮納入更多的實際要素,如考慮需求的不確定性、成本時間屬性,以及考慮產品生產中的學習效應等。
參考文獻
[1]DELLAERT N, JEUNET J, JONARD N. A genetic algorithm to solve the general multi-level lot-sizing problem with time-varying costs[J]. International Journal of Production Economics, 2000, 68(3): 241-257.
[2]YOU M, XIAO Y Y, ZHANG S Y, et al. Modeling the capacitated multi-level lot-sizing problem under time-varying environments and a fix-and-optimize solution approach[J]. Entropy, 2019, 21(4): 377.
[3]XIAO Y Y, ZHANG R Q, ZHAO Q H, et al. A variable neighborhood search with an effective local search for uncapacitated multilevel lot-sizing problems[J]. European Journal of Operational Research, 2014, 235(1): 102-114.
[4]LOLLI F, MESSORI M, GAMBERINI R, et al. Modelling production cost with the effects of learning and forgetting[J]. IFAC-PapersOnLine, 2016, 49(12): 503-508.
[5]JABER Y M, PELTOKORPI J. The effects of learning in production and group size on the lot-sizing problem[J]. Applied Mathematical Modelling, 2020, 81: 419-427.
[6]郭映彤. 研制與批產訂單混合調度建模及優化方法研究[D]. 上海: 上海交通大學, 2016.
GUO Y T. Modeling and optimizing methods research on hybrid scheduling of Ramp;D and batch production[D]. Shanghai: Shanghai Jiao Tong University, 2016.
[7]于雪磊, 瞿華. 基于“龍芯”處理器軍用裝備產品平臺化、產品化研究及實踐[J]. 中國航天, 2022(S1): 62-66.
YU X L, QU H. Research and practice of platformisation and productisation of military equipment products based on longchip processor[J]. Aerospace China, 2022(S1): 62-66.
[8]張變亞. 多品種多階段生產系統問題建模優化分析[J]. 蘭州石化職業技術學院學報, 2021, 21(2): 18-23.
ZHANG B Y. Modeling optimization analysis of multiple varieties and stages production system problems[J]. Journal of Lanzhou Petrochemical Polytechnic, 2021, 21(2): 18-23.
[9]陳洪根, 閆鑫, 張艷, 等. 生產系統維修管理-統計過程控制-經濟生產批量集成優化研究綜述[J]. 現代制造工程, 2020(10): 148-155, 12.
CHEN H G, YAN X, ZHANG Y, et al.Review on the integrated optimization of maintenance management amp; statistical process control amp; economic production quantity on production system[J]. Modern Manufacturing Engineering, 2020(10): 148-155, 12.
[10]王得水, 黃漫玲. 淺析復雜電子信息系統裝備產品批產生產線建設[J]. 裝備制造技術, 2019(11): 209-212.
WANG D S, HUANG M L. Brief analysis on construction of batch production line of complex electronic information system equipment product[J]. Equipment Manufacturing Technology, 2019(11): 209-212.
[11]王中婧. 某軍工批產MAO制造項目的進度管理研究[D]. 成都: 電子科技大學, 2018.
WANG Z J. Study on progress management in a military batch production of the MAO manufacturing project[D]. Chengdu: University of Electronic Science and Technology of China, 2018.
[12]胡楠楠, 南方. 低成本批產商業通信衛星用元器件保障模式探索[J]. 數字通信世界, 2018(8): 247-259.
HU N N, NAN F. Exploration of component assurance models for low-cost wholesale production of commercial communications satellites[J]. Digital Communication World, 2018(8): 247-259.
[13]YU Y, TANG J F, SUN W, et al. Reducing worker(s) by converting assembly line into a pure cell system[J]. International Journal of Production Economics, 2013, 145(2): 799-806.
[14]KAKU I. Is SERU a sustainable manufacturing system?[J]. Procedia Manufacturing, 2017, 8: 723-730.
[15]SUER G, ULUTAS B, KAKU I, et al. Considering product life cycle stages and worker skill level in SERU production systems[J]. Procedia Manufacturing, 2019, 39: 1097-1103.
[16]XIE Y, ZHOU S H, XIAO Y Y, et al. A β-accurate linearization method of Euclidean distance for the facility layout problem with heterogeneous distance metrics[J]. European Journal of Operational Research. 2018, 265(1): 26-38.
[17]XIAO Y Y, ZHANG Y, KULTUREL-KONAK S, et al. The aperiodic facility layout problem with time-varying demands and an optimal master-slave solution approach[J]. International Journal of Production Research, 2021, 59(17): 5216-5235.
[18]YOU M, XIAO Y Y, ZHANG S Y, et al. Optimal mathematical programming for the warehouse location problem with Euclidean distance linearization[J]. Computers amp; Industrial Engineering, 2019, 136(C): 70-79.
[19]XIAO Y Y, YUAN Y Y, ZHANG R Q, et al. Non-permutation flow shop scheduling with order acceptance and weighted tardiness[J]. Applied Mathematics and Computation, 2015, 270(1): 312-333.
[20]ZHANG R Q, ZHANG L K, XIAO Y Y, et al. The activity-based aggregate production planning with capacity expansion in manufacturing systems[J]. Computers amp; Industrial Engineering, 2012, 62(2): 491-503.
[21]周宏明, 高順, 張祥雷, 等. 帶緩沖串行生產系統預防性維護建模及運行參數優化研究[J]. 運籌與管理, 2022, 31(1): 22-29.
ZHOU H M, GAO S, ZHANG X L, et al.Preventive maintenance modeling and operation parameter optimization for series production systems with intermediate buffers[J]. Operations Research and Management Science, 2022, 31(1): 22-29.
[22]陸志強, 張之磊. 串聯生產系統維護在線決策與緩沖分配聯合優化[J]. 同濟大學學報(自然科學版), 2021, 49(3): 431-439.
LU Z Q, ZHANG Z L. Joint optimization of on-line decisionmaking for maintenance and buffer allocation for serial production system[J]. Journal of Tongji University (Natural Science), 2021, 49(3): 431-439.
[23]方鵬, 李芳, 劉凡, 等. 考慮產品質量控制的生產系統預防性維護策略聯合優化研究[J]. 上海理工大學學報, 2021, 43(5): 497-504.
FANG P, LI F, LIU F, et al.Optimization of preventive maintenance strategy for production system considering product quality control[J]. Journal of University of Shanghai for Science and Techology, 2021, 43(5): 497-504.
[24]ADULYASAK Y, CORDEAU J F, JANS R. The production routing problem: a review of formulations and solution algorithms[J]. Computers amp; Operations Research, 2015, 55(1): 141-152.
[25]CHITSAZ M, CORDEAU J F, JANS R. A branch-and-cut algorithm for an assembly routing problem[J]. European Journal of Operational Research, 2020, 282(3): 896-910.
[26]ALVAREZ A, MIRANDA P, ROHMER S. Production routing for perishable products[J]. Omega, 2022, 111: 102667.
[27]FRIFITA S, AFSAR H M, HNAIEN F. An efficient mat-heuristic algorithm for the dynamic disassembly assembly routing problem with returns[J]. European Journal of Industrial Engineering, 2020, 16(5): 584-617.
[28]MANOUSAKIS E G, KASAPIDIS G A, KIRANOUDIS C T, et al. An infeasible space exploring matheuristic for the production routing problem[J]. European Journal of Operational Research, 2021, 298(2): 478-495.
[29]LI Y T, CHU F, CHU C B, et al. An efficient three-level heuristic for the large-scaled multi-product production routing problem with outsourcing[J]. European Journal of Operational Research, 2019, 272(3): 914-927.
[30]RUSSELL-ROBERT A. Mathematical programming heuristics for the production routing problem[J]. International Journal of Production Economics, 2017, 193: 40-49.
[31]NEVES-MOREIRA F, ALMADA-LOBO B, GUIMARES L, et al. The multi-product inventory-routing problem with pickups and deliveries: mitigating fluctuating demand via rolling horizon heuristics[J]. Transportation Research Part E: Logistics and Transportation Review, 2022, 164: 102791.
[32]MOONS S, RAMAEKERS K, CARIS A, et al. Integrating production scheduling and vehicle routing decisions at the ope-rational decision level: a review and discussion[J]. Computers amp; Industrial Engineering, 2017, 104(2): 224-245.
[33]HUANG M, DU B G, GUO J. A hybrid collaborative framework for integrated production scheduling and vehicle routing problem with batch manufacturing and soft time windows[J]. Computers amp; Operations Research, 2023, 159: 106346.
[34]SHAMAKI B P, ROUX L G. Optimization for sustainable hydrogen production path[J]. Computer Aided Chemical Engineering, 2022, 51: 235-240.
[35]ERDOGAN A, GULER M G. Optimization and analysis of a hydrogen supply chain in terms of cost, CO2 emissions, and risk: the case of Turkey[J]. International Journal of Hydrogen Energy, 2023, 48(60): 22752-22765.
[36]RIERA J A, LIMA R M, KNIO O M. A review of hydrogen production and supply chain modeling and optimization[J]. International Journal of Hydrogen Energy, 2023, 48(37): 13731-13755.
[37]WU J J, ZHANG J, YI W M, et al. Agri-biomass supply chain optimization in north China: model development and application[J]. Energy, 2022, 239(D): 122374.
[38]DE-JONG S, HOEFNAGELS R, WETTERLUND E, et al. Cost optimization of biofuel production-the impact of scale, integration, transport and supply chain configurations[J]. Applied Energy, 2017, 195(6): 1055-1070.
[39]DROFENIK J, PAHOR B, KRAVANJA Z, et al. Multi-objective scenario optimization of the food supply chain—Slovenian case study[J]. Computers amp; Chemical Engineering, 2023, 172: 108197.
作者簡介
楊麗穎(1982—),女,高級工程師,碩士,主要研究方向為成本工程。
楊銳意(1999—),男,博士研究生,主要研究方向為可靠性系統工程。
崔新豪(2000—),男,碩士研究生,主要研究方向為復雜系統建模與優化。
張思悅(1996—),女,博士研究生,主要研究方向為物流網絡系統優化。
陳 練(1980—),男,高級工程師,碩士,主要研究方向為經濟性分析。
肖依永(1973—),男,副教授,博士研究生導師,博士,主要研究方向為系統優化理論與經濟性工程。

