多星協同觀測遺傳-演進雙層任務規劃算法

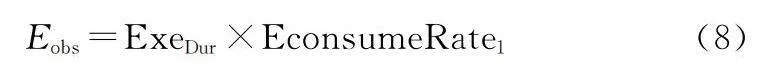
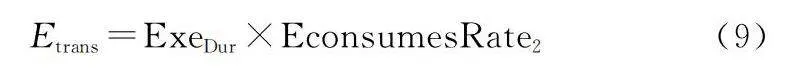
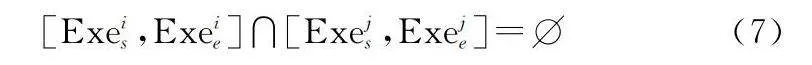
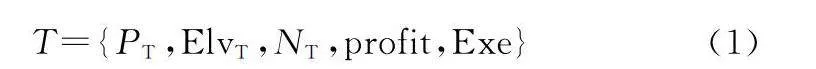
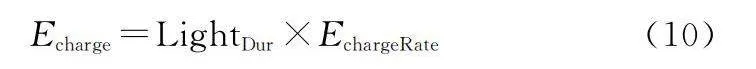
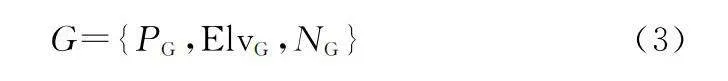
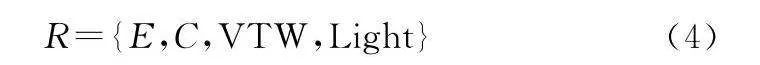
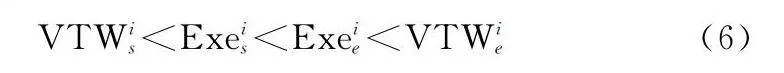
摘要： 多星協同任務規劃方法是天基衛星系統管控的關鍵支撐。圍繞多星協同對地觀測任務展開分析，首先建立多星協同任務規劃模型，包括衛星軌道參數、約束條件和待觀測目標點等;其次設計了遺傳-演進雙層求解架構，將多星任務規劃問題拆解為頂層多星任務分配問題和底層單星任務調度問題，上層采用基于引導的多種群遺傳算法（multi-population genetic algorithm， MPGA），將啟發式結果融入到任務分配算法中，下層采用改進遺傳算法對單星任務調度問題進行求解;最后針對適用性問題，設定隨機和均勻分布兩組目標，采用不同衛星數量設計實驗驗證了遺傳-演進雙層求解框架的有效性。

關鍵詞： 衛星任務規劃; 遺傳-演進架構; 多種群遺傳算法; 并行算法

中圖分類號： V 19

文獻標志碼： A

DOI：10.12305/j.issn.1001-506X.2024.06.22

Genetic-evolutionary bi-level mission planning algorithm for multi-satellite cooperative observation

LI Yangyang， LUO Junren， ZHANG Wanpeng^*， XIANG Fengtao

（College of Intelligence Science and Technology， National University of Defense Technology， Changsha 410073， China）

Abstract： Multi-satellite cooperative mission planning method is a key node in the space-based satellite system architecture. Firstly， the multi-satellite cooperative for Earth observation mission is analyzed and a multi-satellite cooperative mission planning model is established， including satellite orbit parameters， constraint conditions， and target points to be observed. Then， a genetic-evolutionary bi-level solution architecture is designed， which decomposes the multi-satellite mission planning problem into a top multi-satellite mission assignment problem and a bottom single-satellite mission scheduling problem. The upper level uses the guided multi-population genetic algorithm （MPGA） to integrate the heuristic results into the task allocation algorithm， and the lower level uses the improved genetic algorithm to solve the single-satellite task scheduling problem. Finally， aiming at the applicability problem， two groups of objectives are set randomly and uniformly distributed， and experiments are designed with different numbers of satellites to prove the effectiveness of the genetic-evolutionary bi-level solution framework.

Keywords： satellite task planning; genetic-evolutionary architecture; multi-population genetic algorithm （MPGA）; parallel algorithm

0 引 言

天基對地觀測衛星作為一種全球偵察工具，跨越了傳統地域的限制，從而可以極大范圍地觀測重點靜態目標、時敏（非時敏）移動目標和應急響應觀測目標等，在應對自然災害、遠程通信、軍事戰爭之中可以發揮更為重要的作用。近年來，隨著天基系統不斷發展，相較于單顆衛星對地觀測任務，多星協同觀測通過合理利用衛星資源完成對地目標的觀測，可以帶來巨大的效益。如何利用好現有衛星觀測資源，實現多星有效協同，則是現有學者不斷進行探索的主要研究方向^［1］。

多星協同對地觀測是一類非確定性多項式問題，采用傳統的啟發式方法難以獲得有效問題解。現有學者主要采用的不同方法可以分為以下4類：

（1） 精確算法：通過采用數學方法精確求解此類約束滿足問題，實現最優化的任務規劃。文獻［2］設計了混合整數線性規劃問題模型，在8天時間內驗證了20多個任務的執行。文獻［3］采用數學求解器CPLEX對云層的不確定干擾進行分析，優化一個傳感器的時間為600～1 200 s，對兩個傳感器的優化時間在2 000～3 000 s，對大規模任務處理較為乏力。文獻［4］采用分支定界算法計算由高分辨率和低分辨率衛星組成的星群的調度，驗證了算法在25個目標下的有效性。文獻［5］采用多級路徑縮減動態規劃方法來處理衛星調度問題，并在中、小型問題中可獲得最優解。由于衛星規劃數據量巨大，精確求解方法為適應小規模計算場景，對于大規模任務不可行。

（2） 啟發式方法：一些學者通過設定啟發式函數，借用啟發式方法完成任務分配^［6］，利用人為設定的規劃規則實現衛星調度。文獻［7］研究了自適應大鄰域搜索算法，自適應選擇運算方式可以取得較好效果。文獻［8］研究了云層不確定環境下的啟發式衛星任務調度方法。文獻［9］設計了10種不同的分配策略，并使用支持向量機在不同場景下選用分配策略。文獻［10］利用蟻群算法來實現任務分配，通過精確算法求解單星任務調度，二者交互實現衛星任務規劃。文獻［11］設計了基于直接插入、移位、回溯、刪除和重新插入的啟發式算法，將長期、大規模的問題轉化為短期、小規模的問題，提高了原有調度方案的可調度性和應急響應的敏感性。但是此類方法實現的只是可行解，需要充分考慮不同要素設計啟發式規則，對人的經驗要求高，不能適應不同任務場景下的任務規劃問題。

（3） 機器學習方法：這類方法需要預先獲取任務規劃數據，規劃質量的好壞不僅取決于算法的能力，同時也取決于將數據輸入到機器學習算法的歷史數據方案的質量。文獻［12］提出一種雙向門控循環單元，實現衛星任務的預測。文獻［13］提出一種基于深度學習的方法來實現對衛星任務的規劃，設計了長短時記憶網絡來實現決策過程，通過5組實驗加以驗證。文獻［14-16］利用深度強化學習對衛星任務進行規劃。文獻［17］設計了一種數據驅動的多顆敏捷衛星調度方法，通過基于增廣拓撲的合作神經演化方法實現衛星任務分配的概率預測，實現任務合理分配。機器學習方法充分利用了已有數據來進行預測，隨著任務不斷到達，不斷進行決策，屬于“來一個解決一個”^［18］的任務規劃方法，對大規模任務同時決策存在局限性，難以滿足多用戶不同的任務需求。

（4） 基于反饋的方法：通過將多星任務規劃分為多星任務分配和單星調度兩個階段^［19］，在分配之后實行任務調度，將結果反饋到任務分配方案，再改進任務分配方案，實現任務迭代完成，是一個不斷演化的過程^［20-21］。文獻［22］通過結合遺傳算法和關鍵路徑算法，將關鍵路徑算法反饋的單星任務調度結果反饋到分配結果中并進行優化，實現多星多任務的分配。文獻［23］將任務規劃分為任務預規劃與任務重規劃兩個階段，通過蟻群優化算法完成多星任務規劃。

本文主要圍繞多星協同任務規劃這一問題展開，設計遺傳-演進雙層算法框架，利用基于引導的多種群遺傳算法（multi-population genetic algorithm， MPGA）求解多星協同任務分配，采用并行遺傳算法求解單星任務調度，從而實現雙層衛星協同規劃。

1 問題分析與建模

1.1 觀測問題描述

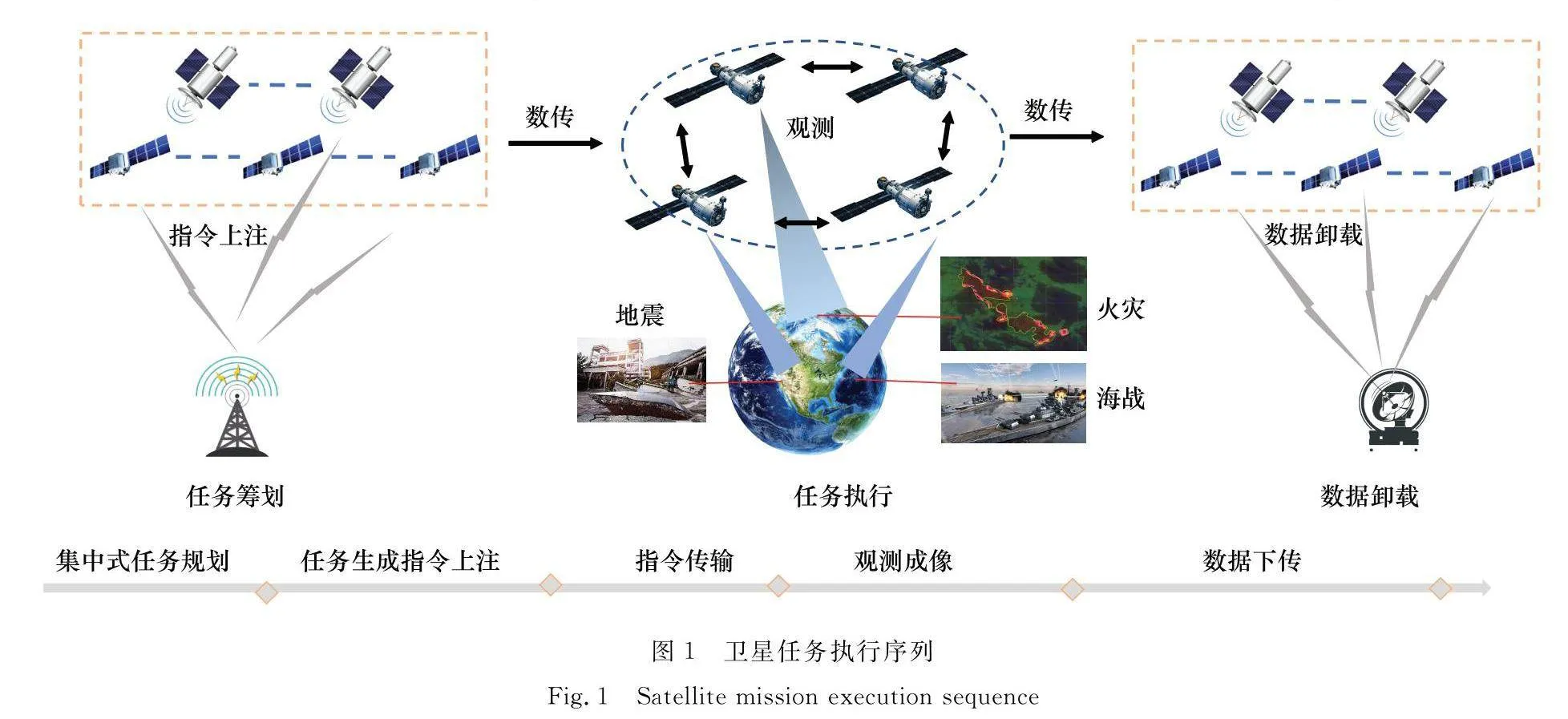
天基觀測系統旨在利用現有衛星，通過高中低軌衛星協同配合，合理利用遙感衛星和通信衛星，通過協同配合減少系統反應延時，提高系統響應速度。當前單個衛星獲取遙感數據之后需要通過存儲數據直到與地面站可見時將其下傳到地面，但是衛星回訪周期長，對地可見時間短，例如一顆1 000 km的衛星回訪周期大約為6 300 s，衛星可見時間還不到回訪周期的1/10。李德仁等^［24］提出通導遙一體化的部署格局，將通信導航遙感衛星通過組網聯系起來，充分發揮天基系統的效能。本文按照此類設計思想，構建通信和遙感相互協調的天基系統衛星執行任務流程，以滿足未來系統設計要求。通過通信衛星星座和遙感衛星的配合，可快速準確完成衛星任務。可以將多星協同問題分為兩部分，其中一部分為遙感衛星之間通過相互分工，完成對地目標的觀測，提高觀測收益;另一部分為應用遙感衛星和通信衛星的相互配合，高效完成衛星觀測任務并及時傳輸，本文暫不考慮。

圖1為天基系統衛星任務執行流程，分為任務籌劃、任務執行和數據卸載3個階段。通過在地面接收任務指令，充分利用地面龐大的計算能力，將任務合理分配到適合觀測的衛星，通過任務上注到中低軌通信網絡，將指令傳輸到遙感衛星，通過遙感衛星的傳感器采取任務數據，再通過中低軌衛星通信網絡將數據傳輸到地面用戶，采用此類流程可以減少系統響應時間，提高任務觀測能力，部分學者的研究從分布式的方法展開^［25］，但是現存衛星的計算能力還不足以支撐系統全局優化，本文設計一種集中式的任務規劃方法，提高天基系統整體收益，主要針對遙感衛星任務規劃階段展開研究。

多星協同任務規劃可定義為一類帶約束的組合優化問題^［26］。衛星對地觀測通過調用觀測載荷，在指定區域采用一定的偏轉角度，實現對地面目標的探測，現有載荷主要分為合成孔徑雷達載荷、高分紅外載荷、可見光衛星載荷、高光譜衛星載荷。本文假設一顆衛星可攜帶多種觀測載荷，可根據觀測環境自主調用載荷，主要研究衛星對地目標觀測過程，實現具有演進機制的多星協同任務分配方法。

衛星對地觀測問題需要綜合考慮一系列因素，基于反饋的任務規劃方法在兩階段的設計需要進行合理籌劃。其中，多星任務分配需要將目標任務分配給合理的衛星，完成衛星和目標的最優組合，使得產生的收益最大;單星任務調度問題，需要滿足衛星運行電量、存儲等一系列資源約束，通過兩個階段不斷迭代優化，高質量完成衛星任務。為簡化計算，本文將所有任務目標設定為點目標，且目標之間相互獨立，衛星觀測一次即可完成任務，無需重復觀測，暫不考慮衛星任務規劃指令上注后通過通信衛星自主發送到遙感衛星的過程，單顆遙感衛星調度只考慮存儲和內存約束對衛星調度產生的影響。

1.2 任務規劃模型構建

多星協同任務規劃需要考慮衛星任務屬性、地面目標屬性以及衛星與地面目標之間的關系，衛星與外界環境的交互關系，因此任務規劃模型將圍繞各類集合以及集合之間的約束關系建立。

（1） 任務集合

T={P_T，Elv_T，N_T，profit，Exe}（1）

式中：P_T={latitude，longitude，height}代表目標的經緯度以及高度;Elv_T表示目標的最小仰角;N_T表示目標數量;profit表示任務執行收益，根據衛星任務緊急情況設定;Exe表示任務執行時間。

（2） 衛星集合

S={Name，N_S，property}（2）

式中：Name為衛星名稱;N_S為衛星數量;property為衛星軌道根數。

（3） 地面站集合

G={P_G，Elv_G，N_G}（3）

式中：P_G={latitude，longitude，height}代表地面站的經緯度和高度;Elv_G表示地面站最小仰角;N_G表示地面站數量。

（4） 資源集合

R={E，C，VTW，Light}（4）

式中：VTW表示資源間可見時間窗口，VTW={VTW_G，VTW_T，VTW_E，VTW_S，VTW_Dur}，VTW_G表示衛星對地面站可見時間窗，VTW_T表示衛星對地觀測可見時間窗，VTW_S表示可見時間窗開始時間，VTW_E表示可見時間窗結束時間，VTW_Dur表示可見時間窗持續時間;Num表示可見時間窗數量;E表示衛星電量;C表示衛星存儲;Light表示衛星光照。決策變量為

x_ij=x₁₁x₁₂…x_1m

x₂₁x₂₂…x_2m

x_n1x_n2…x_nm

表示將m個任務分別分配給n顆衛星。0≤x_ij≤1，0表示任務i不在衛星j上執行;1表示任務i在衛星j上執行。

（5） 目標函數

為最大化遙感衛星觀察任務總收益，本文將目標設定為相同收益，因此衛星任務規劃問題可轉換為最大化觀測任務目標數量問題。

J=∑mi=1∑nj=1x_ij（5）

1.3 約束條件形式化

基于以上模型集合和變量，衛星任務規劃需要滿足時間、電量、存儲約束。以下主要介紹各約束條件。

（1） 時間窗約束

通過衛星工具包（satellite tool kit， STK）獲取衛星與地面目標的可見時間窗口，如圖2所示，虛線代表可見時間窗，實線代表任務執行時間。時間窗內執行任務相互影響，執行時間安排可能會存在沖突，因此需要合理選擇任務開始執行區間，減少沖突，提高觀測能力。

時間窗口選擇：對于任意任務i，任務執行時間必須在可見時間窗內，即

VTWⁱ_slt;Exeⁱ_slt;Exeⁱ_elt;VTWⁱ_e（6）

① 對于時間窗按順序排列互不影響的情況

時間窗內執行任務相互獨立，只需按照時間窗順序選擇執行任務即可。如圖2所示，以任務2為例，任務2和任務4、5、7滿足第1種時間窗約束，任務執行順序互不影響。

② 對于時間窗存在重疊區域的情況

同顆衛星先后任務執行時間不能有重疊，即有：

［Exeⁱ_s，Exeⁱ_e］∩［Exe^j_s，Exe^j_e］=? （7）

任務4、5、6、7時間窗口相互重疊，根據任務執行時間長度，選擇如此安排的方式，得到6-4-5的任務執行序列，任務7由于與任務5存在執行時間沖突，衛星難以在同一時間觀測2個目標，因此衛星需要按照規劃適當舍棄無法觀測的目標。

實驗將地面站窗口考慮在時間窗口內，同衛星對地目標一同參與計算，當出現沖突時，優先對地面站傳輸數據，再進行觀測。

（2） 電池電量約束

衛星電量作為可以再生能源，需要在規劃時進行考慮，由于半影時間較短，僅假設在本影時間衛星無法進行充電，在光照區可以通過太陽能發電板生成衛星執行任務所需電量。將電量作為考慮因素。

電池消耗=執行時間×消耗速率

拍攝消耗：

E_obs=Exe_Dur×EconsumeRate₁（8）

下傳消耗：

E_trans=Exe_Dur×EconsumesRate₂（9）

電量生成=光照時間×生成速率：

E_charge=Light_Dur×E_chargeRate（10）

衛星電量=當前電量+電量生成-電量消耗lt;電池容量：

E_total=E_current+E_charge－E_consumelt;E_capacity（11）

（3） 存儲空間約束

衛星在發射時內存容量已經固定，衛星容量固定使得衛星不能無限制地執行對地目標觀測，因此需要在對地目標觀測過程中考慮內存約束，觀測活動對于存儲空間的占用以及通過地面站對數據的卸載從而恢復存儲的過程加以合理考慮。

存儲消耗=拍攝時間×消耗速率

C_consume=Exe_Dur×C_consumeRate（12）

存儲釋放=傳輸時間×傳輸速率

C_release=Exe_Dur×C_transRate（13）

存儲約束不可以超出最大存儲容量

C_total=C_current+C_release－C_consumelt;C_capacity（14）

（4） 任務執行次數約束

∑mi=1∑nj=1x_ijlt;1（15）

表示對任務x_ij觀測最多不超過1次。

2 遺傳-演化雙層求解框架

2.1 雙層算法框架設計

將多星協同觀測進行拆分，采用雙層算法框架進行求解，上層為任務分配過程，下層為單星任務調度過程，上層為下層提供任務分配結果，下層為上層反饋任務調度數據，通過上下層的迭代演化任務規劃結果，提高系統對目標的觀測能力。

遺傳算法作為進化算法，適合在大規模尋優問題中尋求解決方案，通過設定合理的染色體結構，模仿達爾文進化過程，利用染色體的交叉變異等操作形成新的個體，采用個體保留方式找到適應度大的個體并保存下來，在不斷優化迭代過程中找到全局最優解。針對遺傳算法存在的早熟問題，本文在雙層架構中采用不同的手段進行消解。設定兩階段遺傳算法，在上層采用基于引導的MPGA，通過融入部分啟發式方法作為引導，減少無效搜索策略空間，種群間的相互交互可以實現算法快速收斂。在下層采用并行單星調度遺傳算法，采用精英保留和輪盤賭方法進行子代選擇，根據染色體情況采用不同的交叉變異策略，求得單星最優任務調度方案。兩個階段通過不同的策略尋優，共同實現所得結果全局最優^［27］。

針對衛星任務特點，將多星任務規劃問題拆分為多星任務分配和單星任務調度問題，合理設定兩階段的迭代過程，從而尋得全局最優解。

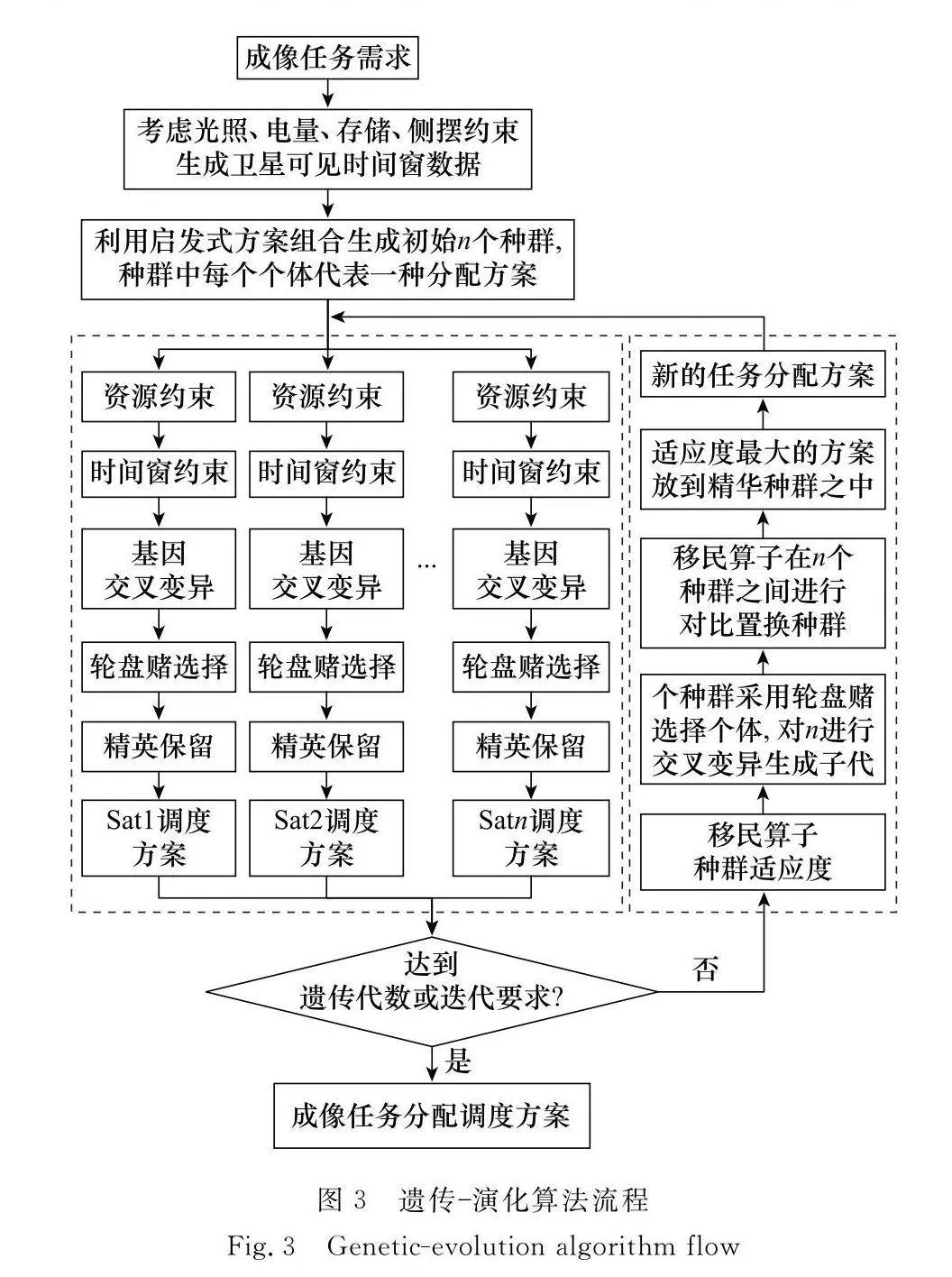
算法流程如圖3所示。

步驟 1 通過STK生成衛星光照、電量存儲約束、生成對地目標可見時間窗數據。

步驟 2 按照目標任務序列，隨機選擇執行任務的衛星的編號，生成任務分配初始方案個體，將一定數量的個體組合成為一個種群，同時利用啟發式函數生成一定數量的個體，插入到種群之中通過初始化生成N個種群。

步驟 3 將步驟2中指定的任務按照衛星編號進行分配，通過并行化方法在單星任務調度中利用遺傳算法，計算出每顆衛星通過執行任務觀測得到的目標數目。

步驟 4 利用計算所得的單星任務觀測任務總數生成初始種群的適應度函數，在N個種群內部采用輪盤賭選擇個體，進行交叉概率為p_m和變異概率為p_c的產生子代種群的操作。

步驟 5 利用移民算子在種群之間進行對比，在每個種群中，將本種群內最好的個體替換其他種群中最差的個體。

步驟 6 選出適應度最大的種群方案，并將其放到精華種群之中形成新的任務分配方案

步驟 7 若滿足迭代要求，結束循環生成任務分配方案，若不滿足則返回步驟3繼續按照順序執行。

2.2 多星任務分配問題

MPGA^［28］通過多個種群同時搜索擴大了搜索空間，避免遺傳算法陷入局部最優的情況中，在種群內部通過交叉變異算子進行迭代更新，在不同種群之間通過移民算子相互聯系，實現種群外的交互。本文多星任務分配策略采用基于引導的MPGA，在多種群的基礎上，融合了啟發式規則作為引導，減少了許多無效的搜索，提高了算法的效率。以下介紹MPGA的過程。

（1） 編碼：染色體采用十進制編碼，染色體長度按照任務序號順序排列，采用隨機選擇的方式，設定每個變量為衛星數量，通過隨機選擇分配衛星編號同時結合啟發式函數作為引導形成任務分配方案，通過對方案不斷迭代，找到多星協同任務分配方案。啟發式規則可從文獻［5］中提取。

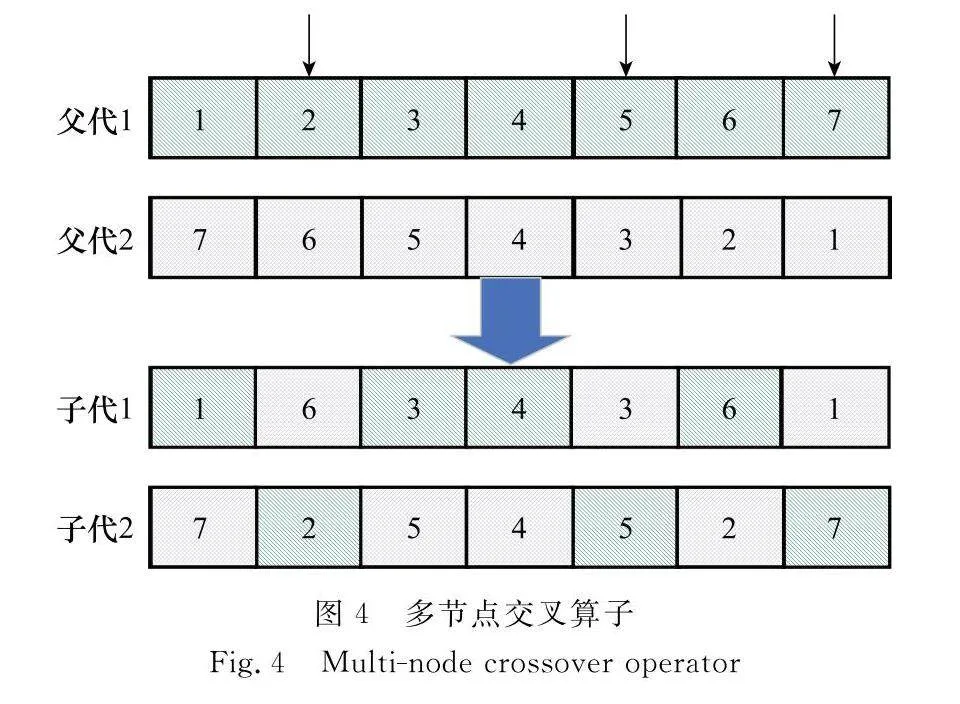
（2） 交叉算子：交叉采用多節點交叉，如圖4所示，按照交叉概率，兩條染色體在多個節點位置進行基因互換，從而產生新的子代染色體。

（3） 變異算子：變異通過設定變異概率，在多個基因位置根據概率，采用離散變異算子用特定的概率對每個基因進行變異。

（4） 選擇算子：在種群內采用輪盤賭的方式，將選擇好的個體移入下一代組成下一代染色體種群。在種群外使用人工選擇算子，選擇適應度最高的種群作為精華種群，同時記錄下種群中最優的個體作為迭代的判斷條件。

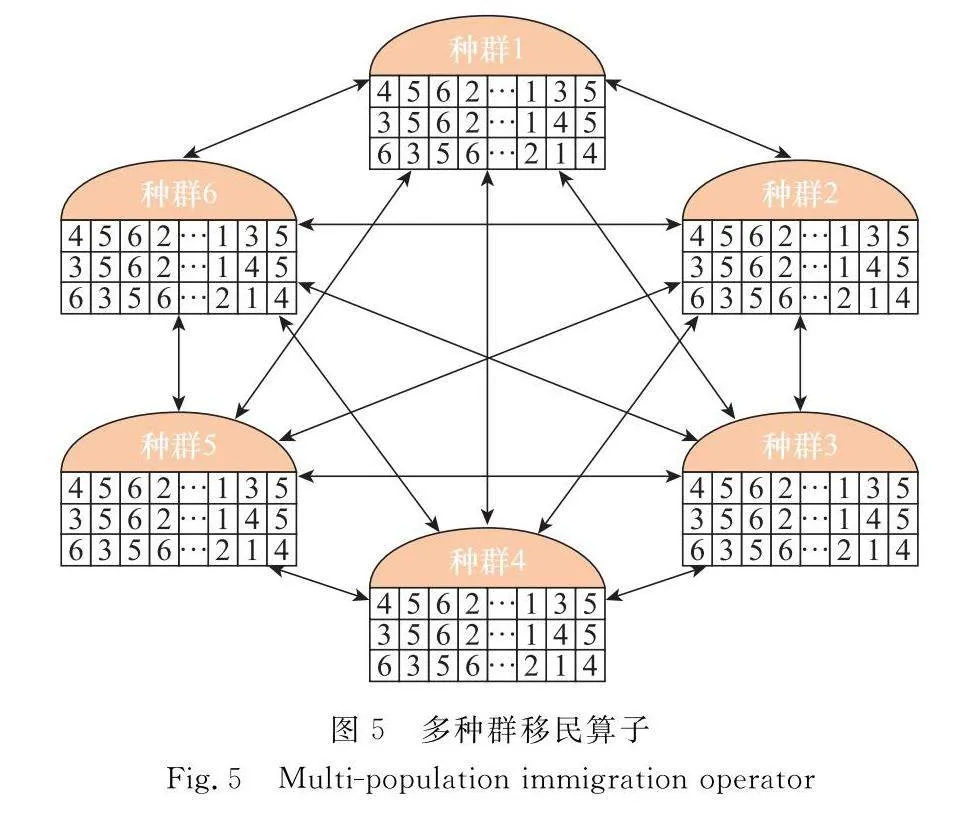
（5） 移民算子：通過利用單星任務調度方案得到生成適應度函數值，如圖5所示，將每個種群中適應度最好的染色體插入到其他種群中，替換掉最差的染色體編碼，實現種群的更新。

（6） 適應度函數：設置為追求觀測目標效益最大化或者實現任務完成數量最大化。本文將目標設定為同類目標，任務收益相同，因此以適用任務完成率來計算適應度。

MPGA的具體步驟如算法1所示。

2.3 單星任務調度問題

單顆衛星任務調度問題需要在滿足時間窗口約束、內存約束、電量約束條件下找到可以完成任務數量最多、任務效益最大的任務規劃方案。

本文采用并行遺傳算法，將任務分配的方案分配給單顆衛星，再交由特定的衛星執行相應任務，采用并行的方式，同時完成多顆衛星對地觀測的計算，減少系統響應時間，快速完成單星任務調度，返回到多星任務分配階段作為適應度的指標輸入，對分配結果進行迭代，實現反饋的任務分配方案，不斷對方案進行演進，直到滿足觀測目標。

以下介紹單星調度的過程。

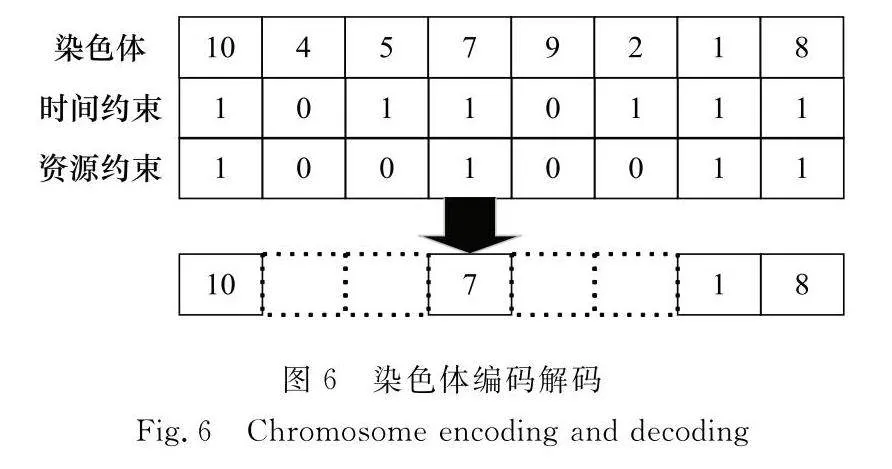
（1） 編碼過程：分配給單個衛星的任務，對每個目標選取一個時間窗，按照時間窗的結束時間進行升序排列，采用整數型編碼方式組成一條染色體編碼，過程如圖6所示。

（2） 解碼過程：利用時間約束，剔除不可行的基因，篩選后再根據資源約束，剔除不滿足資源約束的基因，得到可執行任務序列編碼。

（3） 交叉變異策略：不滿足時間約束的基因通過部分變異，不需進行交叉操作，在原有基礎上達到盡可能大的滿足時間約束，對于滿足時間約束同時滿足資源約束的基因，通過交叉和變異的方法將時間影響范圍內的基因組進行局部優化，提高執行任務數量，對于滿足時間約束但是不滿足資源約束的情況，資源未被合理分配，此時需要通過全局的交叉和變異實現全局優化。

（4） 選擇策略：輪盤賭選擇算子。

（5） 精英保留策略：利用此類策略可以保存基因型良好的染色體從而避免被交叉和變異破壞，通過一定概率將父代良好的染色體保留下來，直接組成子代種群。

（6） 適應度函數：將單顆衛星對所分配任務的完成情況作為適應度函數進行計算。

單星調度遺傳算法的具體步驟如算法2所示。

3.1 實驗設計

設定衛星資源參數，將每個目標點任務消耗設定在32 MB到64 MB之間隨機分布，下傳電量為5 J/s，對地下傳輸速率為1 MB/s，充電速率為5 W，衛星存儲容量為16 GB，電池容量為20 000 J。衛星資源參數如表1所示。

目標設置：組1在南北緯60°的區域內，均勻分布的162個目標，組2在南北緯60°的區域內，隨機分布300個點目標，用于衛星觀測。成像時間設置為2022-03-21T00：00：00-2022-03-22T00：00：00，仿真天數為1天。圖7和圖8分別為第1組和第2組點目標分布。

為方便衛星任務信息收集，在全國范圍內選擇了國內5個重要城市坐標，如表2所示。

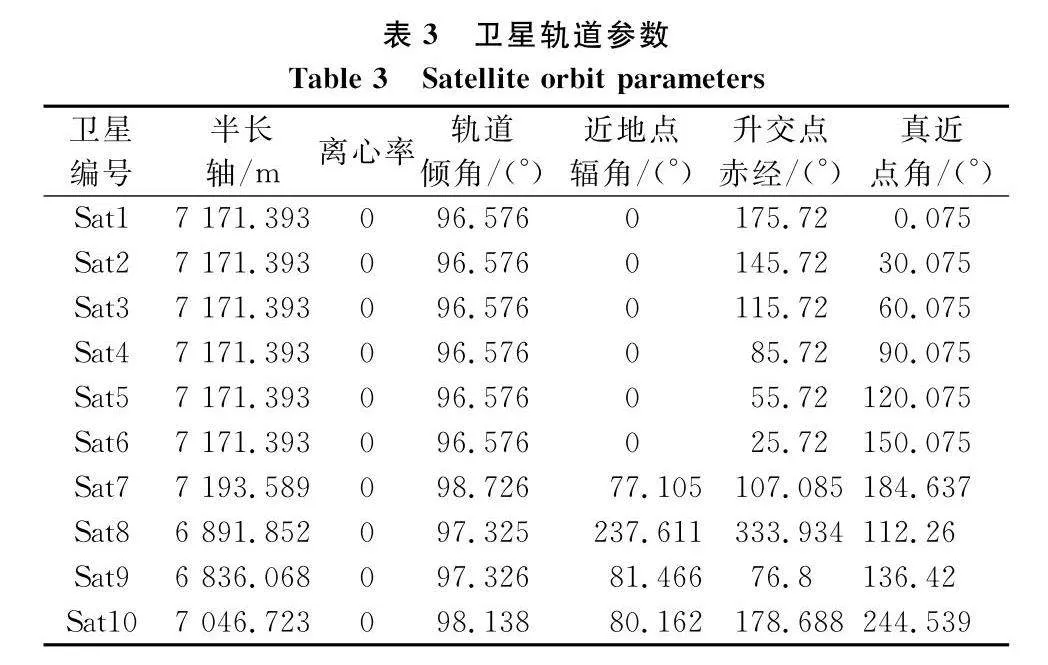
衛星軌道采用表3所示的10顆衛星軌道參數分別從文獻［29］和文獻［30］中提取，組1采用前6顆衛星，組2采用10顆衛星。

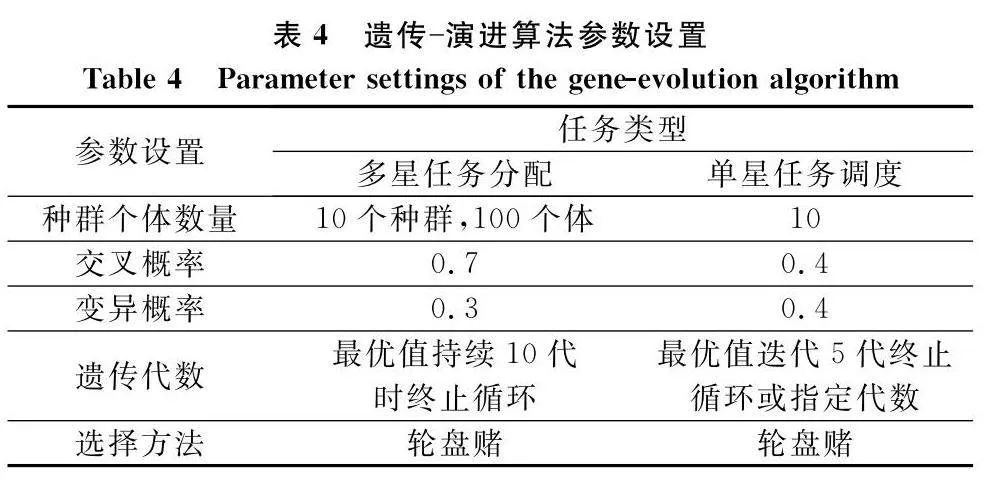
設置MPGA參數，如表4所示。提供10個種群，每個種群有10個個體，變異概率設定為0.3，最大迭代次數為最優值持續10次時終止循環時的次數，單星調度遺傳算法設定個體數量為10，交叉概率和變異概率均為0.4，終止條件為當遺傳代數持續100代或最優值持續5次時終止循環。

3.2 實驗結果

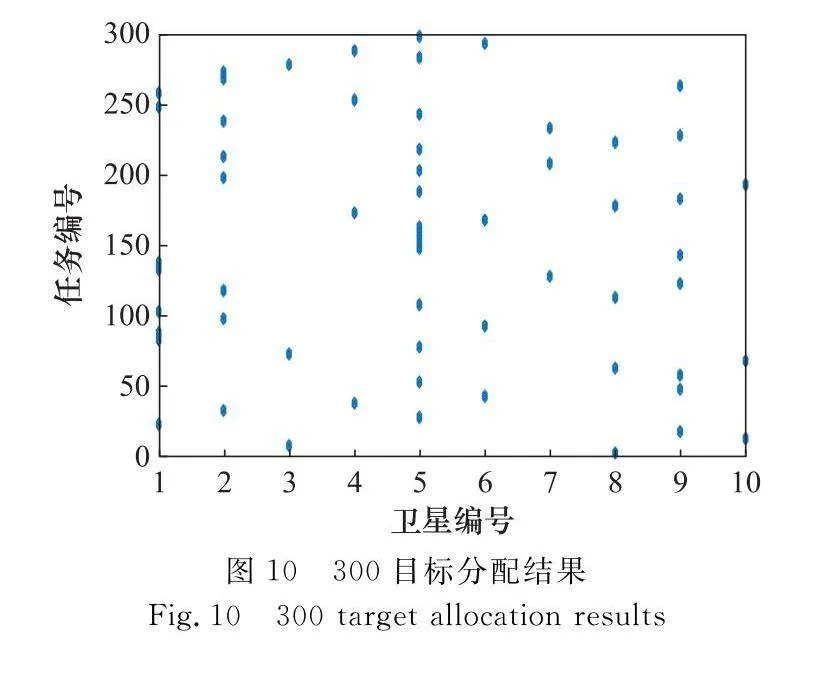
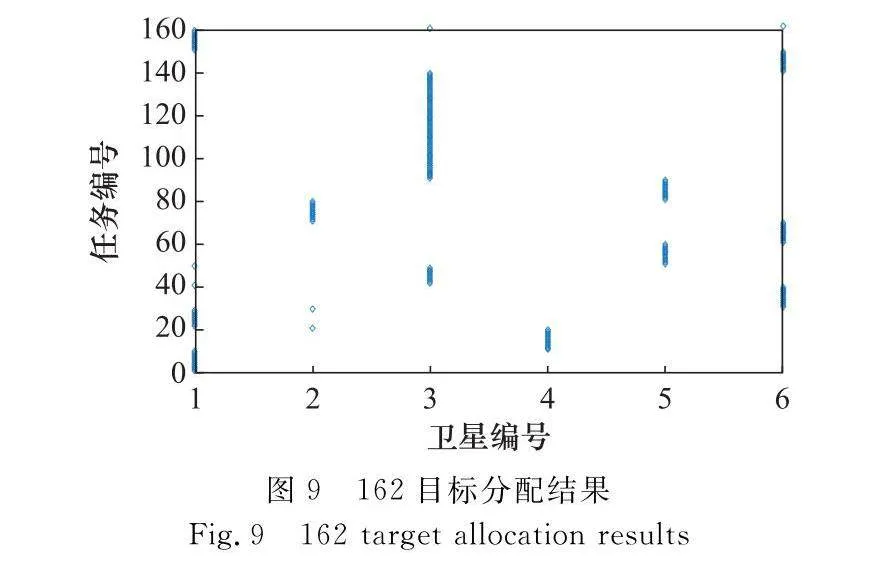
通過算法運行得到圖9和圖10所示的任務分配結果，結果顯示每顆衛星均分到相應任務且隨著任務數量的增加，分配結果也更均衡。

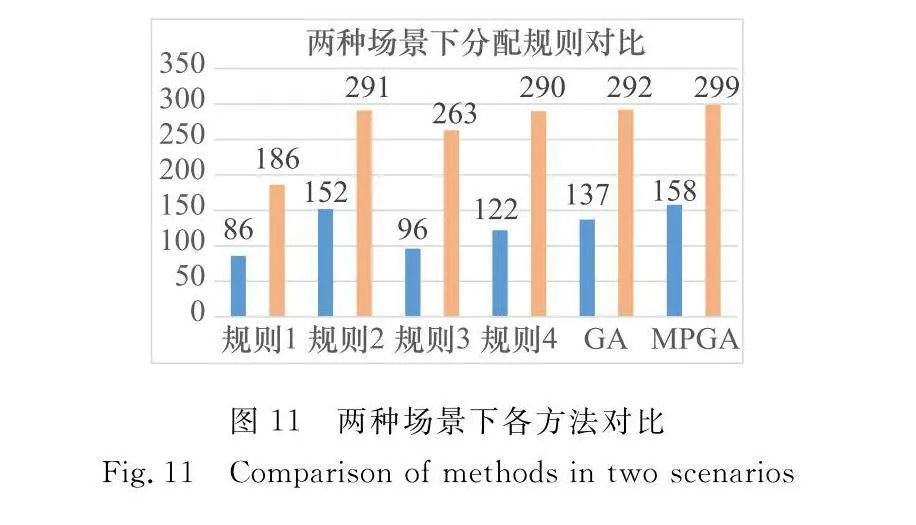
將標準遺傳算法（genetic algorithm， GA）、MPGA同啟發式算法對比，所得結果如圖11所示。其中規則1為任務分配給持續時間最長的衛星的啟發式方法，規則2為任務分配給可見時間最早的衛星的啟發式方法，規則3為任務分配給可見時間最晚的衛星的啟發式方法，規則4為任務分配給可見次數最多的衛星的啟發式方法。結果顯示部分啟發式規則對于任務設定不適用，得到的結果較差。MPGA在兩組實驗設計中均可以取得優異結果。

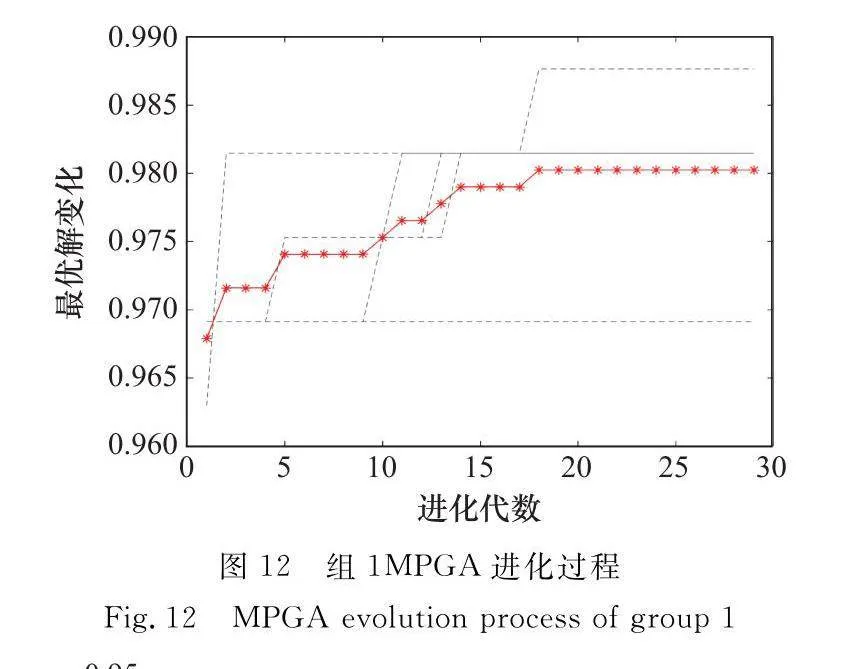
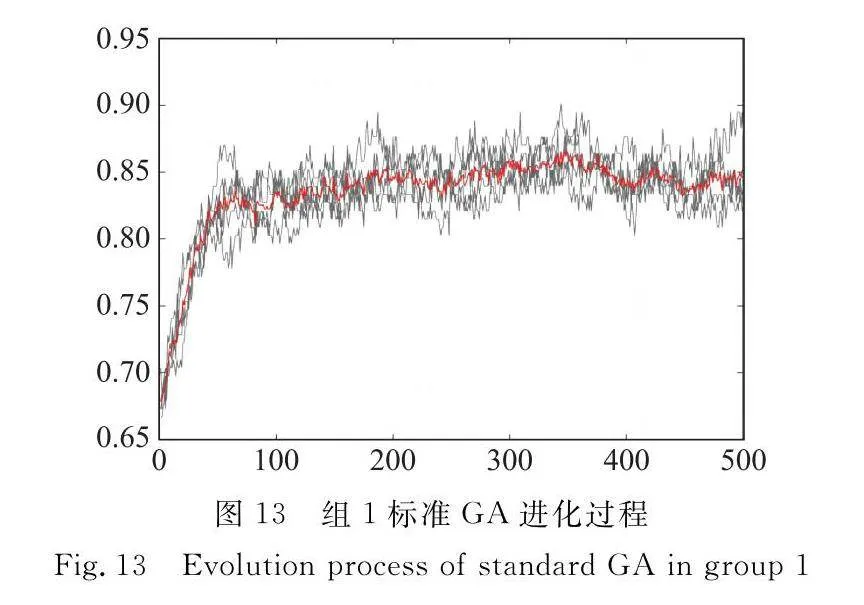
在組1的實驗場景下，所得結果如圖12和圖13所示，在5次實驗中，MPGA均較好地完成任務，平均任務完成率為98.02%，符合任務觀測要求。對比標準GA，迭代次數500代執行5次實驗任務平均完成率為86.54%，完成率提高11.98%，同時相比于標準GA 500代還未達到預期效果，基于引導的MPGA在迭代次數上在平均收斂不到30代即可達到觀測要求。

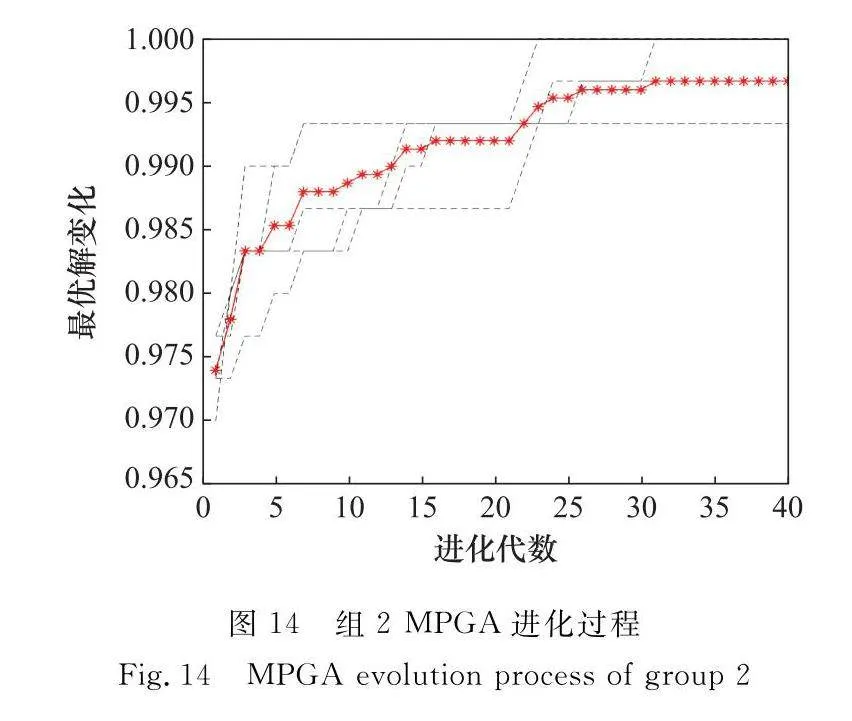
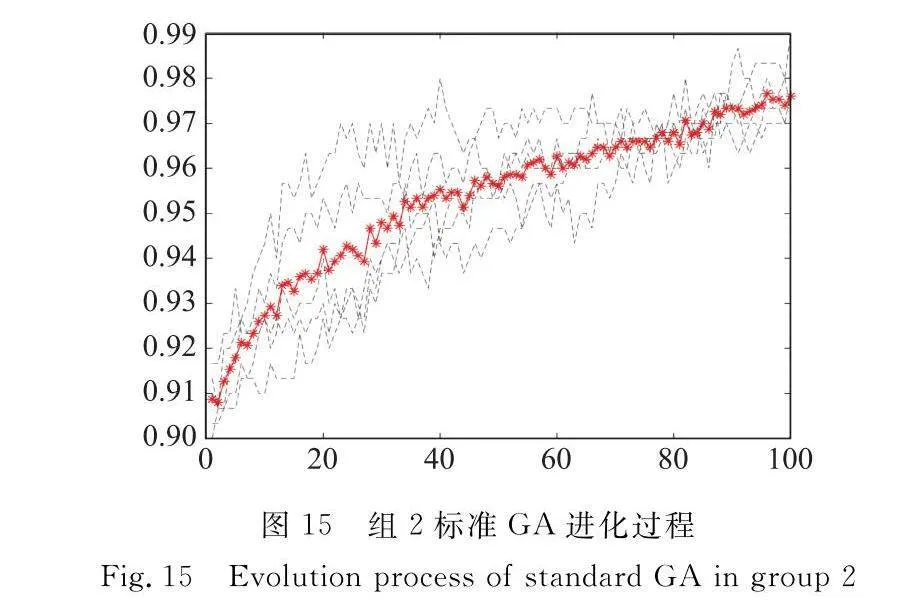
在組2實驗場景下，得到如圖14和圖15的實驗結果。進行5組實驗，通過啟發式函數的引導作用，MPGA任務平均完成率達到99.67%，相較于100代標準GA提高了2%，MPGA在30代基本已完成收斂，較標準GA更快。

3.3 結果分析

從任務分配結果來看，無論是第1組的162個目標、6顆衛星還是第2組的300個目標、10顆衛星，任務分配階段均可以根據衛星能力較為均勻地分布下去。通過與啟發式方法的對比，可見本文算法效果更優，設計的任務分配方案更適合使用。

結合兩組實驗證明，基于引導的MPGA適用于多場景多星任務分配問題，無論是在隨機分布、均勻分布場景下，或是在衛星數目變化的條件下，均可取得好的任務分配效果，隨著任務數量的提升，觀測完成率不斷提高。利用本文算法，可實現單星全局最優調度以及多星全局最優分配，為多星協同問題提供了可不斷演進的解決方案。

4 結 論

多星協同任務規劃是一類典型的非確定性多項式問題，考慮了電量、內存、時間窗等資源約束，本文通過設計遺傳-演進雙層求解架構將問題拆解，在上層任務分配階段采用基于引導的MPGA，通過融入啟發式規則引導，算法收斂代數少，計算結果優異;在下層單星調度階段采用并行GA，將任務分配的結果遞交各執行衛星，通過并行方式完成調度計算，采用反饋式的演化方法，不斷迭代，得到更好的分配結果，以滿足任務需求。

天基系統的星上部分應用還包括星間傳輸、任務注入以及數據卸載的過程，本文僅考慮遙感衛星對地面站進行數據下傳的過程。下一步，將繼續深入研究多星協同任務傳輸方法，充分利用星間鏈路，減少傳輸過程中的延時，提高天基系統任務響應率。

參考文獻

［1］ZHENG Z X， GUO J， GILL E. Distributed onboard mission planning for multi-satellite systems［J］. Aerospace Science and Technology， 2019， 89： 111-122.

［2］XIAO Y Y， ZHANG S Y， YANG P， et al. A two-stage flow-shop scheme for the multi-satellite observation and data-downlink scheduling problem considering weather uncertainties［J］. Reliability Engineering and System Safety， 2019， 188： 263-275.

［3］VALICKA C G， GARCIA D， STAID A， et al. Mixed-integer programming models for optimal constellation scheduling given cloud cover uncertainty［J］. European Journal of Operational Research， 2019， 275 （2）： 431-445.

［4］CHU X G， CHEN Y N， TAN Y J. An anytime branch and bound algorithm for agile earth observation satellite onboard scheduling［J］. Advances in Space Research， 2017， 60（9）： 2077-2090.

［5］LIU Z B， FENG Z R， REN Z G. Route-reduction-based dynamic programming for large-scale satellite range scheduling problem［J］. Engineering Optimization， 2019， 51（11）： 1944-1964.

［6］PELLERIN R， PERRIER N， BERTHAUT F. A survey of hybrid metaheuristics for the resource-constrained project scheduling problem［J］. European Journal of Operational Research， 2020， 280（2）： 395-416.

［7］HE L， LIU X L， LAPORTE G， et al. An improved adaptive large neighborhood search algorithm for multiple agile satellites scheduling［J］. Computers amp; Operations Research， 2018， 100： 12-25.

［8］WANG J J， HU X J， HE C. Reactive scheduling of multiple EOSs under cloud uncertainties： model and algorithms［J］. Journal of Systems Engineering and Electronics， 2021， 32（1）： 163-177.

［9］YAO F， LI J T， CHEN Y N， et al. Task allocation strategies for cooperative task planning of multi-autonomous satellite constellation［J］. Advances in Space Research， 2019， 63（2）： 1073-1084.

［10］WU G H， LUO Q Z， DU X， et al. Ensemble of meta-heuristic and exact algorithm based on the divide and conquer framework for multi-satellite observation scheduling［J］. IEEE Trans.on Aerospace and Electronic Systems， 2022， 58（5）： 4396-4408.

［11］SUN H Q， XIA W， HU X X， et al. Earth observation satellite scheduling for emergency tasks［J］. Journal of Systems Engineering and Electronics， 2019， 30（5）： 931-945.

［12］陳浩， 羅棕， 杜春， 等. 一種基于Bi-GRU的衛星對地觀測 任務可調度性預測方法［J］. 湖南大學學報（自然科學版）， 2021， 48（6）： 88-95.

CHEN H， LUO Z， DU C， et al. A prediction method for schedulability of satellite earth observation task based on Bi-GRU［J］. Journal of Hunan University （Natural Science Edition）， 2021， 48（6）： 88-95.

［13］PENG S， CHEN H， DU C， et al. On board observation task planning for an autonomous earth observation satellite using long short-term memory［J］. IEEE Access， 2018， 6： 65118-65129.

［14］WANG H J， YANG Z， ZHOU W G， et al. Online scheduling of image satellites based on neural networks and deep reinforcement learning［J］. Chinese Journal of Aeronautics， 2019， 32（4）： 1011-1019.

［15］WANG X， WU J， SHI Z， et al. Deep reinforcement learning-based autonomous mission planning method for high and low orbit multiple agile earth observing satellites［J］. Advances in Space Research， 2022， 70（11）： 3478-3493.

［16］HUANG Y X， MU Z C， WU S F， et al. Revising the observation satellite scheduling problem based on deep reinforcement learning［J］. Remote Sensing， 2021， 13（12）： 2377.

［17］DU Y H， WANG T， XIN B， et al. A data-driven parallel scheduling approach for multiple agile earth observation satellites［J］. IEEE Trans.on Evolutionary Computation， 2019， 24（4）： 679-693.

［18］杜永浩， 邢立寧， 姚鋒， 等. 航天器任務調度模型， 算法與通用求解技術綜述［J］. 自動化學報， 2021， 47（12）： 2715-2741.

DU Y H， XING L N， YAO F， et al. Survey on models， algorithms and general techniques for spacecraft mission scheduling［J］. Acta Automatica Sinica， 2021， 47（12）： 2715-2741.

［19］ZHU W M， HU X X， XIA W， et al. A two-phase genetic annealing method for integrated Earth observation satellite sche-duling problems［J］. Soft Computing， 2019， 23（1）： 181-196.

［20］ZHAO M， LI D C. A hierarchical parallel evolutionary algorithm of distributed and multi-threaded two-level structure for multi-satellite task planning［J］. International Journal of Automation and Control， 2020， 14（5/6）： 612-633.

［21］LI Z L， LI X J. A multi-objective binary-encoding differential evolution algorithm for proactive scheduling of agile earth observation satellites［J］. Advances in Space Research， 2019， 63（10）： 3258-3269.

［22］毛李恒， 鄧清， 劉柔妮， 等. 針對多星多任務仿真調度的關鍵路徑遺傳算法［J］. 系統仿真學報， 2021， 33（1）： 205-214.

MAO L H， DENG Q， LIU R N， et al. CPM-GA for multi-sate-llite and multi-task simulation scheduling［J］. Journal of System Simulation， 2021， 33（1）： 205-214.

［23］QI J T， GUO J J， WANG M M， et al. A cooperative autonomous scheduling approach for multiple earth observation satellites with intensive missions［J］. IEEE Access， 2021， 9： 61646-61661.

［24］李德仁， 丁霖， 邵振峰. 面向實時應用的遙感服務技術［J］. 遙感學報， 2021， 25（1）： 15-24.

LI D R， DING L， SHAO Z F. Application-oriented real-time remote sensing service technology［J］. Journal of Remote Sensing， 2021， 25（1）： 15-24.

［25］WANG C， TANG J H， CHENG X H， et al. Distributed coope-rative task planning algorithm for multiple satellites in delayed communication environment［J］. Journal of Systems Engineering and Electronics， 2016， 27（3）： 619-633.

［26］CHANG Z X， ZHOU Z B， YAO F， et al. Observation scheduling problem for AEOS with a comprehensive task clustering［J］. Journal of Systems Engineering and Electronics， 2021， 32（2）： 347-364.

［27］LI Y Q， WANG R X， YU L， et al. Satellite range scheduling with the priority constraint： an improved genetic algorithm using a station ID encoding method［J］. Chinese Journal of Aeronautics， 2015， 28（3）： 789-803.

［28］ANGELOVA M， PENCHEVA T. Genetic operators’significance assessment in multi-population genetic algorithms［J］. International Journal of Metaheuristics， 2014， 3（2）： 162-173.

［29］張佳唯. 面向航天偵察的任務優先級模型與算法研究［D］. 長沙： 國防科技大學， 2018.

ZHANG J W. Research on task priority model and algorithm for space reconnaissance［D］. Changsha： National University of Defense Technology， 2018.

［30］于龍江， 吳限德， 毛一嵐， 等. 分布式遙感衛星任務分配的合同網絡算法［J］. 哈爾濱工程大學學報， 2020， 41（7）： 1059-1065.

YU L J， WU X D， MAO Y L， et al. Task allocation for distributed remote sensing satellites based contract network algorithm［J］. Journal of Harbin Engineering University， 2020， 41（7）： 1059-1065.

作者簡介

李陽陽（1998—），男，碩士研究生，主要研究方向為智能決策、體系演進。

羅俊仁（1989—），男，博士研究生，主要研究方向為多智能體學習、對抗團隊博弈。

張萬鵬（1982—），男，研究員，博士，主要研究方向為大數據智能、智能演進。

項鳳濤（1983—），男，副教授，博士，主要研究方向為大數據智能、智能演進。