面向階段任務的攜行器材品種確定方法

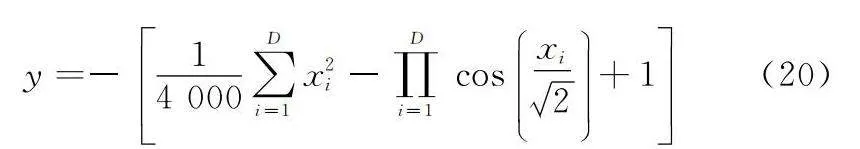
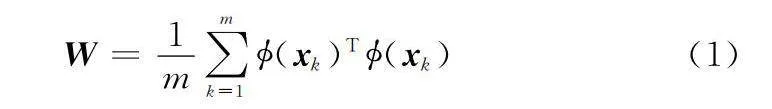
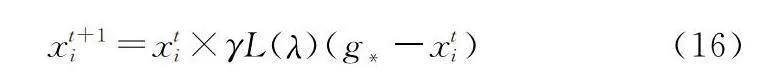
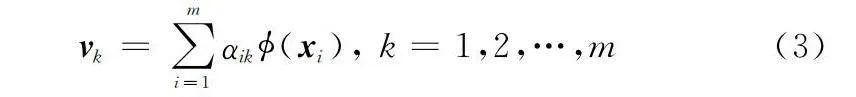
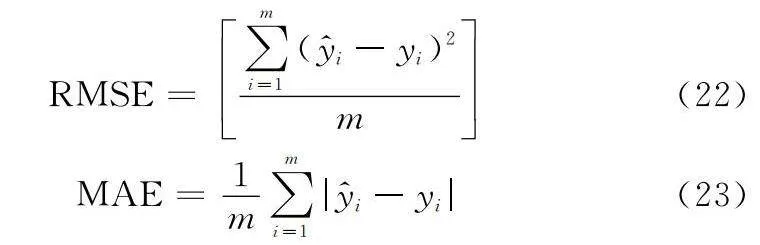
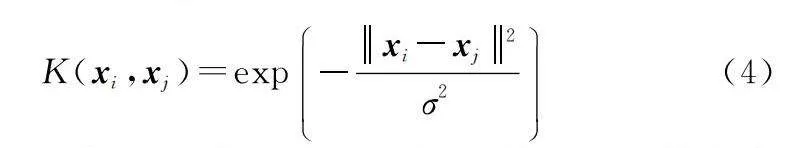
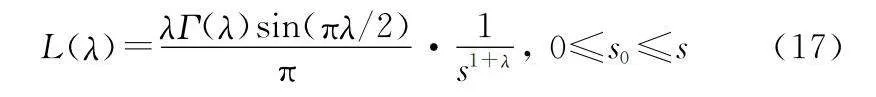
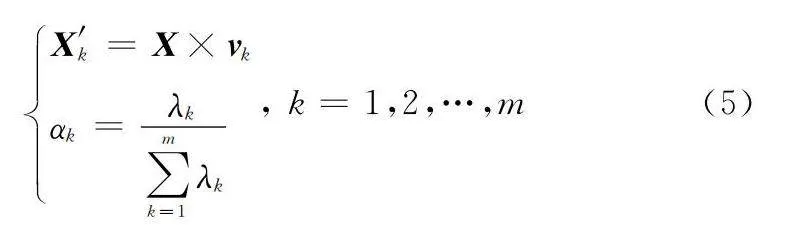
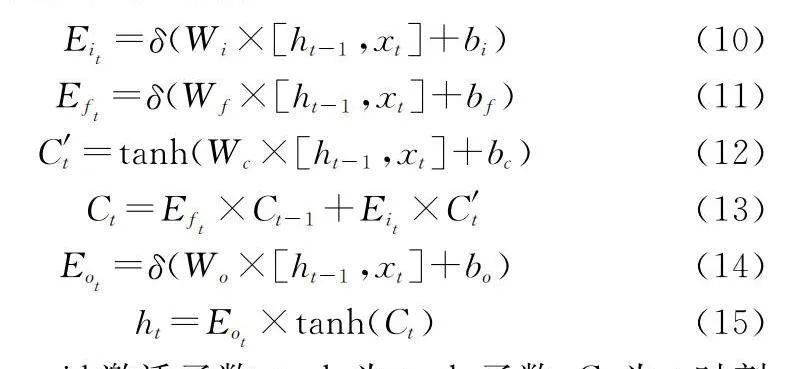
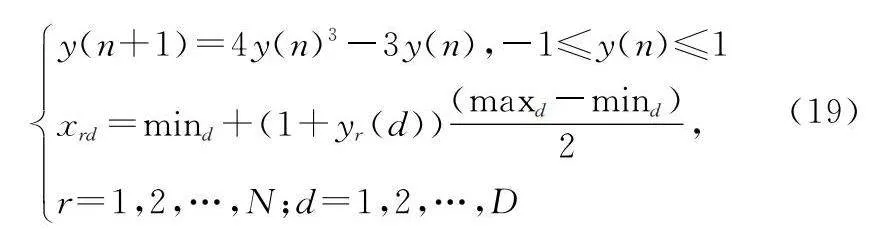
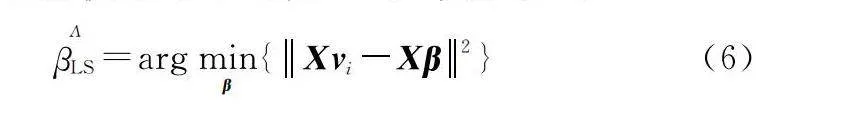
摘要： 維修器材是有效實施維修保障的物質基礎，攜行器材品種確定是開展維修器材攜行決策的關鍵。針對執行階段任務武器裝備維修器材品種多、影響因素復雜且關聯關系不明確造成的攜行器材品種確定困難的現實問題，提出了一種將改進稀疏核主成分分析（sparse kernel principal component analysis， SKPCA）算法與長短時記憶（long short-term memory， LSTM）神經網絡模型相結合的階段任務攜行器材品種確定方法。在分析與任務階段時序相關的攜行器材影響因素及特征指標的基礎上，運用基于彈性懲罰的SKPCA降維算法，對器材特征進行降維分析并得到低維稀疏特征向量，通過縮減數據容量增強特征指標的可解釋性;運用混沌序列改進花授粉算法（flower pollination algorithm， FPA）優化LSTM超參數，構建混沌FPA-LSTM預測模型，精準進行攜行器材品種確定。通過對演習攜行器材品種確定算例分析驗證了所提方法的科學性和可行性。

關鍵詞： 攜行器材; 階段任務; 稀疏核主成分分析; 影響因素分析; 花授粉算法; 長短時記憶神經網絡

中圖分類號： E 92

文獻標志碼： A

DOI：10.12305/j.issn.1001-506X.2024.06.23

Method for determining for carrying material varieties of stage task

WU Weiyi， JIA Yunxian， JIANG Xiangzheng， SHI Xianming^*，

LIU Jie， LIU Bin， DONG Enzhi， ZHU Xi

（Department of Equipment Command and Management， Army Engineering University Shijiazhuang Campus， Shijiazhuang 050003， China）

Abstract： Maintenance material is the basis for effective implementation of maintenance support. It is the key to make decision of carrying material variety. In order to solve the problem which is difficult to determine the carrying material varieties due to various types of material in the stage task， the complex influencing factors and unclear association relationchip， a method for determining carrying material varieties of stage task combined with the improved sparse kernel principal component analysis （SKPCA） and long short-term memory （LSTM） neural network model is proposed. On the basis of analyzing the influencing factors and characteristic indicators of stage task carrying material， an improved SKPCA dimension reduction method based on elastic penalty is proposed which can reduce the material features dimensionality and obtain low-dimensional sparse feature vectors to enhance the data interpretability. The chaotic sequence is used to improve the flower pollination algorithm （FPA） which optimizing the LSTM hyperparameters and the chaotic FPA-LSTM prediction model is constructed. Through the example analysis by the exercise， the scientificity and feasibility of the proposed method are verified.

Keywords： carrying material; stage task; sparse kernel principal component analysis （SKPCA）; influencing factor analysis; flower pollination algorithm （FPA）; long short-term memory （LSTM） neural network

0 引 言

隨著近年來實戰化演習演訓活動的增加，部隊遂行區域任務時應根據不同階段任務需要，攜帶一定品種的維修器材進行攜行保障^［1］。由于執行階段任務的武器裝備具有型號繁多、維修器材品種多樣、影響因素復雜且關聯關系不明確等實際特點，造成了攜行器材品種確定困難的現實問題。如何在不同階段任務下考慮外界條件的約束，結合以往典型階段任務器材消耗使用數據，從眾多種類中快速確定較為科學的攜行器材品種成為亟待解決的難題。

目前，部隊常用的攜行器材品種決策方式大多采用經驗判斷^［2-3］或依據攜行器材標準^［4-5］，在這種決策方式下，器材品種一般以相對恒定的基數包為參考，造成維修器材被不加篩選地輸送到任務地點，出現了大量器材“儲而不用、用而未儲”的現象，大大降低了保障效益，因此有必要探索攜行器材品種確定的相關理論方法，來修正“經驗式”決策方式。學術界對器材品種確定問題進行了大量研究，主要劃分為維修任務分析法和依據零部件自身屬性決策判斷兩種基本方法^［6-7］，其中肖麗麗等^［6］梳理出裝備使用與維修工作分析和維修器材需求確定的關系，給出了器材品種全集確定的方法步驟;文獻［8］通過對裝備系統故障模式影響因素進行分析，結合故障數據建立仿真模型，對器材品種逐一決策判斷，這些方法主要圍繞裝備系統全壽命周期管理特點系統全面地實現對器材品種的確定，但所需理論支撐多、決策程序復雜、流程步驟繁瑣，部隊操作存在一定難度;事實上，維修器材品種確定受多種因素綜合影響，屬于一個多屬性決策問題，大量學者更多地從維修器材屬性影響因素出發，使用模糊綜合評判法^［9-10］、灰色局勢決策理論^［11-12］、價值工程法^［13-14］、相似性方法^［15-16］、需求特征分析^［17-18］等方法進行品種判定，這些方法更多考慮器材單一影響因素或綜合影響因素群來進行品種決策。事實上，一些影響因素與器材的確定目標關聯不大，甚至存在一些噪音因素，對品種確定精度產生負面影響。

考慮到在特定任務情景下必須精簡器材屬性影響因素的數量，重點關注對品種決策貢獻度大的因素，才能縮減輸入數據空間維度，形成低維特征向量，降低品種確定模型的復雜性。核主成分分析（kernel principal component analysis， KPCA）^［19］是一種將多個變量通過核方法轉換成少量變量的多元統計方法，可有效處理非線性數據降維問題;降維數據通過預測模型對特征數據承載信息進行迭代分析，最終得到器材預測結果。近年來，神經網絡技術憑借其原理可靠、精度較高、推導嚴謹、普適通用等優勢在器材需求預測問題中取得了長足發展^［20］。由于維修器材種類繁多、因素復雜且關聯關系不明確，維修器材品種預測難度與時間成本會大幅增加，長短時記憶（long short-term memory， LSTM）神經網絡作為經典的循環神經網絡模型，能夠利用過去的信息數據流解決器材品種決策的長時依賴問題，對輸入向量的處理兼顧了不同階段任務下維修器材的歷史特征信息，考慮了階段任務維修器材的時序相關性，增加了預測模型的可利用信息，有助于提升預測模型的性能和精度^［21］。相比傳統的多因素綜合分析方法，LSTM分類模型更加注重客觀存在和數據本身的時序相關性，能夠有效解決傳統模型受主觀影響大、階段關聯小、預測精度差的問題。

鑒于此，提出了一種將改進稀疏KPCA（sparse KPCA， SKPCA）算法與LSTM模型相結合的階段任務攜行器材品種確定方法。在分析具有任務階段時序相關的攜行器材影響因素及特征指標的基礎上，運用基于彈性懲罰的SKPCA降維算法，對器材特征進行降維分析并得到低維稀疏特征向量，通過縮減數據容量增強特征指標的可解釋性;運用混沌序列改進花授粉算法（flower pollination algorithm， FPA）優化LSTM超參數，構建混沌FPA-LSTM預測模型，最終實現對攜行器材品種的合理確定。

1 階段任務攜行器材影響因素分析

攜行器材品種確定是開展維修器材攜行決策的關鍵，應融入裝備全壽命周期管理的思想，綜合考慮多方面因素影響，主要從裝備因素、任務因素、環境因素和經濟因素4個方面進行攜行器材品種影響因素分析和特征指標的確定，這里重點就影響階段任務完成的典型器材特征指標進行分析。

（1） 裝備因素

裝備因素主要考慮的是裝備設計階段的裝備先天固有屬性，主要包括可靠性、關鍵性、可更換性、可獲取性、體積、質量6個主要指標。其中可靠性通常用平均無故障間隔時間作為指標來評價;關鍵性是指維修器材品種在裝備系統中發揮的作用和對系統性能的影響程度，關鍵性與戰備完好率、任務成功率要求緊密相關，衡量關鍵性因素的一項指標是嚴酷度級別;維修工作復雜性是從維修性角度對部件維修工作復雜程度^［22］、對維修保障資源要求的綜合體現;可獲取性是指在階段任務周期內維修器材是否容易獲取，其與階段任務周期、是否為標準件及貨源穩定性緊密相關，獲取難度大的維修器材應在任務執行前提前儲備。

（2） 任務因素

任務因素主要是從裝備順利完成任務的角度將任務的構成、任務要求與維修器材的需求關系進行描述。通過將任務逐級分解，明確各階段任務構成、任務強度等要求，具體可用任務裝備工作時間這一指標來描述。

（3） 環境因素

裝備所處的任務環境也會產生維修器材需求，任務環境越惡劣，裝備就越容易出現損壞，可以用任務環境要求這一指標描述;除了外在的任務環境，故障裝備能夠快速恢復戰斗力，還需要及時、必備的維修條件和保障條件，也就是應結合裝備維修策略和供應策略進行影響因素的描述，主要用維修時間、供應周轉時間兩個指標來表示。

（4） 經濟因素

經濟因素主要衡量維修器材成本，一般包括器材的采購、存儲、運輸的價值金額。

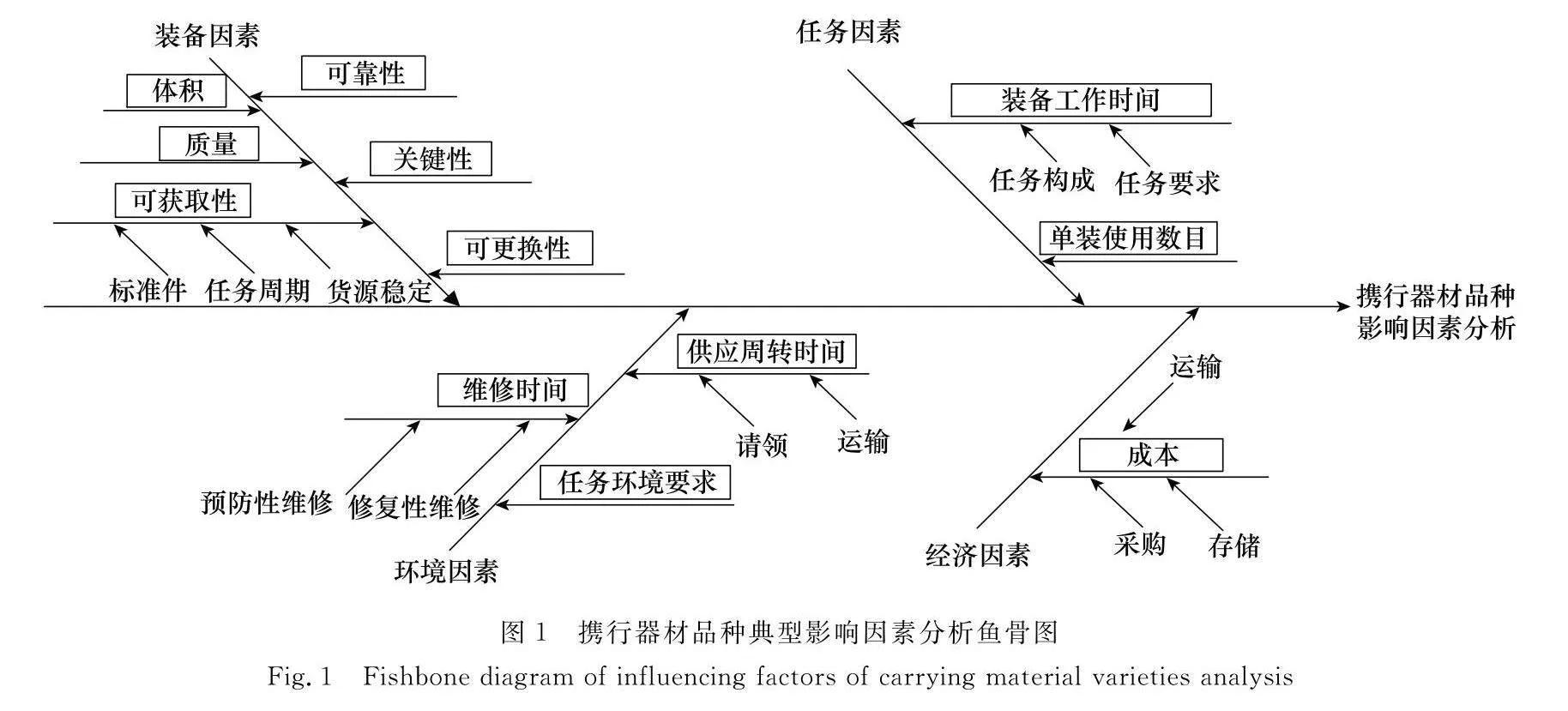
綜上所述，在確定維修器材品種時通常從這4個方面因素通盤考慮，具體可梳理出12個典型特征指標，如圖1所示，矩形框選的就是特征指標。其中，描述各項指標的數據類型不同，有定性的描述指標和定量的度量指標，有連續型變量和離散型變量，根據指標的不同極性可以判斷數據大小與指標效果的好壞^［23］。對于極大值特征，比如器材的可靠性、關鍵性、可更換性等，數據值越大表示該指標越好，相反地，對于極小值特征，比如體積、成本等，數據值越小表示該指標越好。

顯然，在進行攜行器材品種影響因素分析時絕大多數特征指標都是明確的，但唯有一個“階段任務”因素無法由具體的特征指標反映出來。事實上，攜行器材的品種確定與階段任務特點緊密相關，后續階段任務攜行器材品種的確定與前一階段任務器材的消耗具有時序相關性，而這一點在12個特征指標中并未體現，需要在下一步攜行器材品種確定模型中有所體現。

2 SKPCA的特征降維

通過攜行器材影響因素分析得到了12個特征指標，但并不是指標越多越好，實際上一些特征指標與器材的確定目標關聯不大，甚至還存在一些噪音指標，對品種確定精度產生負面影響。精簡維修器材特征維數、縮小數據采樣規模、提升輸入數據質量是器材品種精準確定的基礎。KPCA可有效處理非線性數據，同時使方差貢獻率較為集中。為了進一步提升KPCA的可解釋性和降維效果，融合稀疏主成分分析（sparse principal component analysis， SPCA）彈性懲罰修正的特點^［24］，形成了改進的彈性懲罰SKPCA，增強主成分變量的稀疏性，簡化特征向量的主成分結構，提升特征降維效果。

2.1 KPCA

KPCA作為一種非線性主成分分析（principle component analysis， PCA）方法，其主要思想是：首先將原始樣本矩陣集X={x_k|k=1，2，…，m }輸入后，通過非線性映射函數Φ將X變換到高維特征空間F，F中樣本記作Φ（x_k）;然后在新的特征空間F中完成主成分分析。KPCA的關鍵就是通過引用核函數來替換特征空間中樣本的內積運算，以此處理數據的“維數災難”問題。具體實現過程如下：

將F中樣本的協方差核矩陣W表示為

W=1m∑mk=1?（x_k）^T?（x_k）（1）

對W進行特征矢量分析，得到特征值λ_k和特征向量v_k，表示為

Wv_k=λ_kv_k（2）

將每個樣本做內積，存在一組系數α₁，α₂，…，α_k，使得特征向量v_k處于Φ（x_k）空間中并滿足：

v_k=∑mi=1α_ik?（x_i）， k=1，2，…，m（3）

定義核函數K（x_i，x_j）為徑向基函數，并對核矩陣W進行中心化處理，K（x_i，x_j）表示如下：

K（x_i，x_j）=exp

－x_i－x_j²σ²（4）

式中：σ為方差;‖x_i－x_j‖為歐氏距離;最終得到重構主成分X′_k和方差貢獻率α_k，表示為

X′_k=X×v_k

α_k=λ_k∑mk=1λ_k， k=1，2，…，m（5）

因此，KPCA可以把非線性數據映射到高維空間轉化成線性關系，由于重構主成分數據是空間內所有變量的線性組合，無法突出變量對主成分數據的貢獻率，容易受噪聲干擾，數據間稀疏重構關系體現不明顯^［25］。

2.2 彈性懲罰SKPCA

從式（5）可以發現，重構主成分是原始數據的線性組合，由于特征向量v_k中都是非零元素，造成重構主成分的構成很難解析，致使降維效果有所下降。為了進一步提高KPCA^［26］的可解釋性和降維效果，本文結合KPCA與SPCA算法特點，應用SPCA 模型中的罰函數進行回歸優化，選擇Lasso懲罰的彈性網直接修正，使得改進的SKPCA 不僅可對原始變量進行數據降維，也可以使主成分變得稀疏。具體改進如下：

假設僅考慮前n個主成分（n≤m），KPCA的特征向量矩陣為A_m×n=［v₁，v₂，…，v_n］，稀疏特征向量矩陣表示為B_m×n=［β₁，β₂，…，β_n］。

參照KPCA模型表述，依據式（5）將重構主成分描述為回歸優化問題，并使用最小二乘法回歸求解，則有：

β_LSΛ=argminβ{Xv_i－Xβ2}（6）

式（6）中所用的最小二乘法在回歸精度和不穩定性上存在一定缺陷，需對其進行改進，增加SPCA模型中罰函數L₁范數和L₂范數^［26］進行二次彈性懲罰再回歸，改進后計算式為

β_LSΛ=argminβ

從式（8）可以看出增加的彈性懲罰項為（1-α）∑ⁿ_j=1β_j+α∑ⁿ_j=1β²_j，分別由Lasso懲罰中的L₁和L₂范數構成，實現了系數自由收縮和特征變量降維的效果。

具體的SKPCA改進步驟如下。

步驟 1 樣本矩陣X，確定方差貢獻率閾值θ;

步驟 2 確定核函數K（x_i，x_j）及其參數，對核矩陣W進行中心化處理，得到其特征值λ_k和特征向量v_k;

步驟 3 對空間數據進行主成分分析，按照方差累積貢獻率θ，提取n個主成分并得出降維后的特征向量矩陣A_m×n;

步驟 4 令j≤n，參照式（7）變化為下式

β_LSΛ=argminβ（v_j-β）^TX^TX（v_j-β）+λ_1j∑nj=1|β_j|+λ₂∑nj=1β²_j（9）

得到稀疏特征向量矩陣B_m×n;

步驟 5 依據X^TXB=UDV^T，更新A=UV^T;

步驟 6 重復步驟4和步驟5直至A、B收斂，得到重構的稀疏主成分為X×B。

3 混沌花授粉-LSTM預測模型

連續階段任務下器材消耗具有一定的時序相關性，可采用LSTM處理不同階段任務下器材品種呈現出的時序關系。因此，有必要結合多階段任務剖面分析，針對攜行器材特征指標關聯關系不明的問題，采用LSTM預測模型科學確定階段任務攜行器材品種。

3.1 階段任務剖析

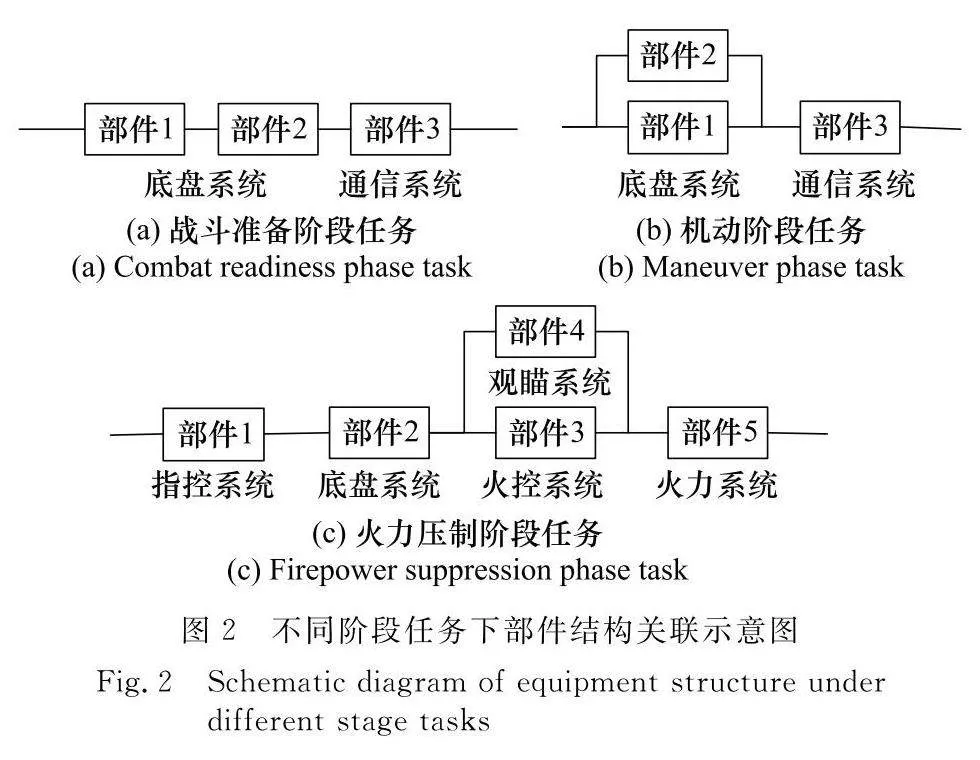
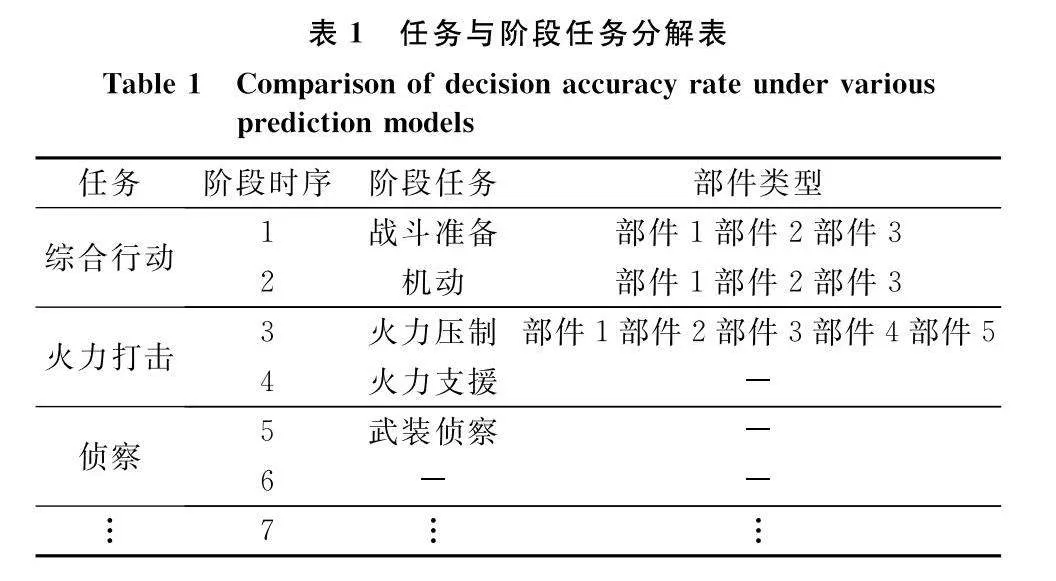
部隊任務就是由多個連續且不重疊的任務階段構成的多階段任務系統^［27］，指揮員會根據任務目的、作戰環境等情況，按時間推進將任務逐級分解為具體階段任務，可以理解為在一定的戰場環境和時空約束下，為完成所承擔的責任或達到特定的作戰目的，而進行的一系列相互關聯的階段行動的有序集合^［27］，如表1所示。從表1可知階段任務的時序邏輯關系構成了整個任務的串行串聯關系。由于裝備系統在不同階段下任務剖面不盡相同，各個部件隨階段任務時間推進會發生功能狀態的持續變化。因此，不同階段任務下裝備損壞主要工作子系統、主要故障原因、部件功能狀態變化具有一定的時序相關性，裝備執行階段任務時主要工作部件結構關聯圖如圖2所示。

3.2 LSTM單元

LSTM神經網絡的核心在于細胞狀態及“門”結構，并將循環神經網絡中隱含層的神經單元轉化為具有門控機制的LSTM單元。這里重點介紹LSTM單元的功能與計算方法，LSTM的預測原理和過程不再贅述。

LSTM神經網絡采用“門”結構選擇性地遺忘或記憶某些時間節點輸出值對當前節點輸出值的影響。假設用x_t和h_t分別表示第t時刻輸入序列值和輸出值，輸入序列x_t為降維后的器材特征屬性形成的序列，每個x_t由低維數據集B_m×n中的β_i和β_i對應的該階段任務下的攜行器材品種確定結果共同構成;E表示每個門的輸出值。LSTM計算過程主要由輸入門、遺忘門、記憶門、輸出門和更新過程 5步組成^［21］，計算公式如下所示：

E_it=δ（W_i×［h_t-1，x_t］+b_i）（10）

E_ft=δ（W_f×［h_t-1，x_t］+b_f）（11）

C′_t=tanh（W_c×［h_t-1，x_t］+b_c）（12）

C_t=E_ft×C_t-1+E_it×C′_t（13）

E_ot=δ（W_o×［h_t-1，x_t］+b_o）（14）

h_t=E_ot×tanh（C_t）（15）

式中：δ為Sigmoid激活函數;tanh為tanh函數;C_t為t時刻的細胞狀態;C′ _t為t時刻的中間細胞狀態;W_f、W_i、W_o、W_c為遺忘門、輸入門、輸出門、中間細胞狀態的各自權重值;b_f、b_i、b_o、b_c為遺忘門、輸入門、輸出門、中間細胞狀態的偏置值。

3.3 混沌FPA優化LSTM超參數

超參數是影響LSTM神經網絡性能的關鍵因素，其中隱含層數目和隱含層神經元數目直接影響著預測模型的擬合度和復雜度，學習率參數影響著預測模型的訓練過程和訓練效果。在實際過程中，超參數的選取基本都是靠經驗確定，造成了一定的隨機性，使預測精度部分下降。FPA具有參數少、穩定性好且不易早熟等優點，并且擁有良好的全部和局部搜索能力。

（1） FPA

Yang^［28］在2012年提出了優化FPA，通過發現自然界中一株植物僅產生一朵花和一朵花粉配子的授粉過程現象總結出FPA，該算法授粉過程采用概率p_c控制^［28］，如下所示：

x^t+1_i=x^t_i×γL（λ）（g*-x^t_i）（16）

式中：x^t_i表示花粉i進行了t次迭代;g*是全局最優位置;γ是比例因子;L（λ）為主步長，具體為

L（λ）=λΓ（λ）sin（πλ/2）π·1s^1+λ， 0≤s₀≤s（17）

式中：λ為步長因子，一般取λ=1.5;Γ（λ）為標準伽馬函數。自然界植物授粉存在局部授粉過程，局部授粉位置更新如下：

x^t+1_i=x^t_i×ε（x^t_j-x^t_k）（18）

式中：x^t_j，x^t_k是花粉j和花粉k進行的第t次迭代;ε為均勻分布產生的隨機數。

（2） 混沌FPA

傳統的FPA多是隨機初始化花粉或配子位置，無法保證花粉位置的遍歷性。為改善種群的多樣性，考慮混沌序列具有高度隨機性和遍歷性的優勢，這里采用三次方映射生成的混沌序列對花粉初始位置進行初始化^［29］，如下所示：

y（n+1）=4y（n）³－3y（n），－1≤y（n）≤1

x_rd=min_d+（1+y_r（d））（max_d－min_d）2，

r=1，2，…，N;d=1，2，…，D（19）

式中：x_rd是第r個個體在第d維上的位置;max_d，min_d是d維搜索空間的上下限;y_r（d）是式（19）中生成的第r個個體的d維。

（3） 混沌FPA測試效果

為驗證本文所提改進的混沌FPA性能和尋優效果，選擇負二階格里旺克測試函數對該算法進行測試。負二階測試函數是一種高維多峰函數^［30］，常被用于測試群智能優化算法效率，主要測試算法擺脫局部極值的能力，函數擁有多個局部極大值點，其理論最優值為0，取值范圍可取［-100，100］，格里旺克測試函數的表達式如下：

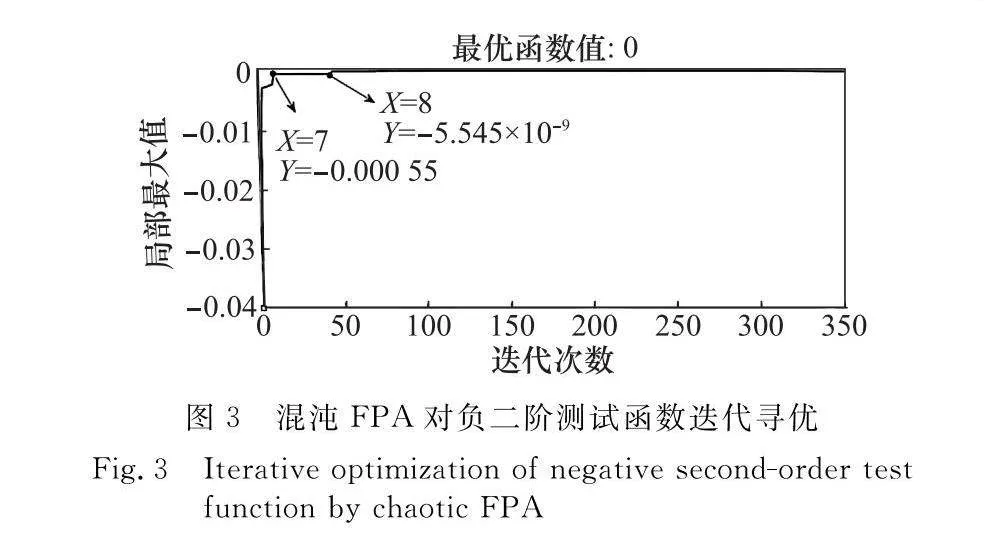
為便于說明算法測試效果，將尋優范圍設定為［-10，10］，D為二維，種群規模設計為25，最大迭代次數為350，轉換概率p_c=0.8，步長縮放因子λ=1.5，改進的混沌FPA尋優效果如圖3所示。

由圖3所示，第1代種群的最大值為-0.033，到第7代時y的最大值為-0.000 55，到了第48代時就接近最大值點0，最優解精確到小數點后10^-9，逼近全局最優值0，證明了混沌FPA的尋優效果。因此，本文引入混沌FPA尋找LSTM超參數包括隱含層數、隱含層神經元數、學習效率3個參數的最優組合，以減少傳統人為主觀定參帶來的弊端影響。

（4） LSTM超參數優化過程

LSTM超參數優化過程包括如下7個步驟：

步驟 1 初始化參數：種群數、最大迭代次數、步長縮放因子、轉換概率及尋優區間范圍;

步驟 2 設置搜索空間維數d=3分別對應3個超參數;

步驟 3 按照混沌FPA中的式（19）給出初始種群，計算其適應度，選出適應度最小值個體為當前種群最優解g_*，適應度函數如下：

fitness=1m∑mi=1?_i－y_i（21）

式中：m為預測的器材品種種類總數;?_i為器材品種預測值;y_i為器材品種實際攜行結果。無論?_i還是y_i，只有0或1兩種取值，其中0表示該種器材不予攜行;1表示該種器材需要攜行;

步驟 4 產生一個均勻分布隨機數rand，比較rand和p_c的大小，若randlt;p_c，參照式（16）執行全局授粉并更新種群;反之，參照式（18）執行局部授粉并更新種群;

步驟 5 計算新種群個體值;

步驟 6 計算新種群的適應度函數值，如果新種群個體適應度值更小，則將新個體納入到下一代種群，并及時更新g_*;

步驟 7 轉入步驟4，直到最大迭代次數為止，得出全局種群最優解g_*及適應度。

4 算例分析

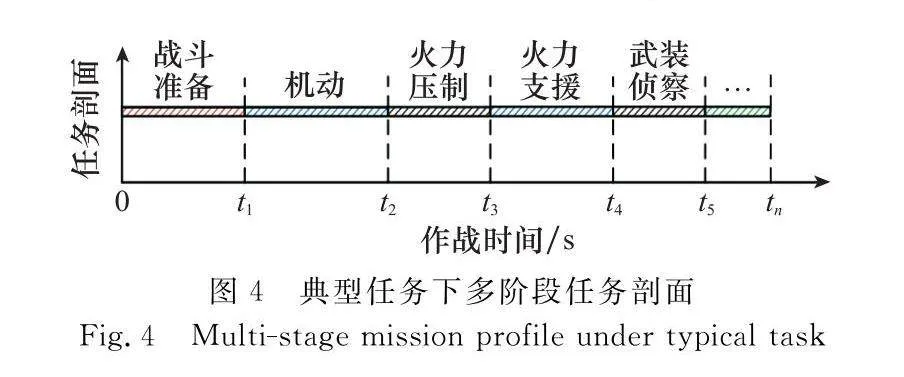
演習部隊接上級通知外出執行作戰任務，將任務周期分為戰斗準備、機動、火力壓制、火力支援、武裝偵察等階段任務，如圖4所示。部隊組織所屬武器裝備協同作戰，不同階段任務下器材消耗隨之變化，所需攜帶的維修器材種類繁多，這就要求該部隊出發前從上千件維修器材中確定攜行器材品種，輔助保障指揮員進行攜行器材品種的快速確定，同時還要求攜行器材品種的決策準確率較高，為下一步開展攜行器材決策提供基礎支撐。

4.1 數據準備及評價標準

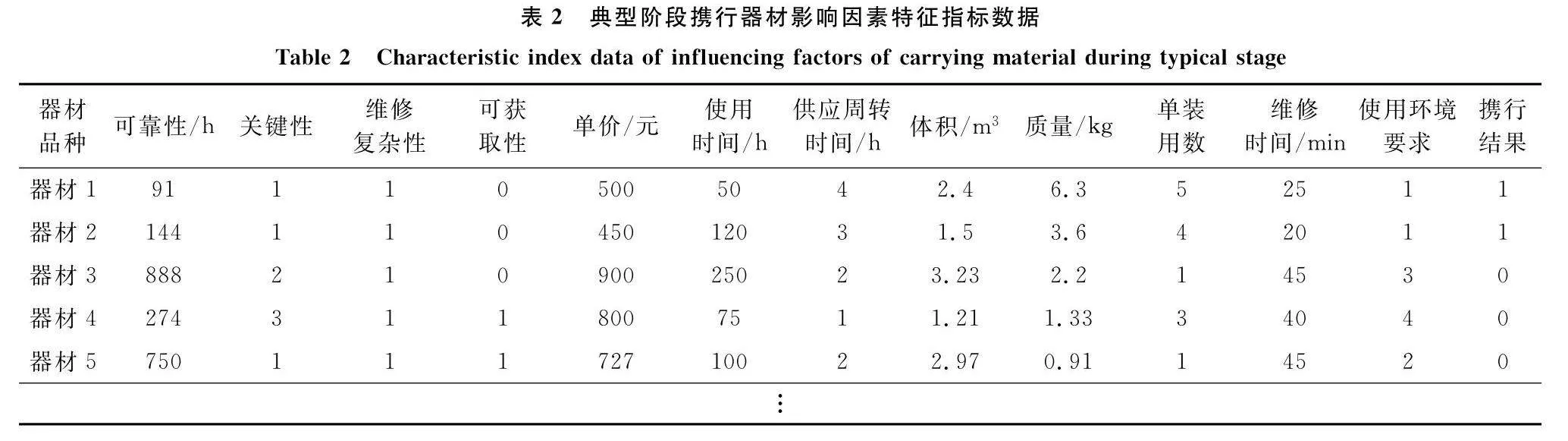
數據來源于往年演習各階段任務下器材使用數據并進行了相應的數據處理。為簡化數據說明，這里選用典型階段任務下攜行器材特征指標數據作為輸入（輸入維數為13），預測數據為下一階段任務的攜行器材品種確定結果（輸出維數為1）。數據集為200種攜行器材樣本，其中隨機選取150組樣本作為訓練樣本，另外50組樣本作為測試樣本。現根據圖1中的攜行器材品種影響因素特征指標對各維修器材進行信息采集，具體數據如表2所示。

由于攜行配置結果中包括很多“0-不攜行”的零值數據，選擇均方根誤差（root mean square error， RMSE）和平均絕對誤差（mean absolute error， MAE）作為評價標準以區分出預測值和實際值之間的離散化和差異化，如下所示：

RMSE=∑mi=1（?_i－y_i）²m（22）

MAE=1m∑mi=1|?_i－y_i|（23）

式中：?_i為器材品種是否攜行的預測值;y_i為器材品種實際攜行結果;m為預測的器材品種類別總數。

另外，為適應部隊精確化保障的任務要求，必須滿足一定的器材品種決策準確率。設器材品種決策準確率C的計算公式為

C=N_CN_T（24）

式中：N_C為器材品種決策正確的數量;N_T為數據集中器材品種類別總數。

4.2 實驗結果

4.2.1 特征降維對比

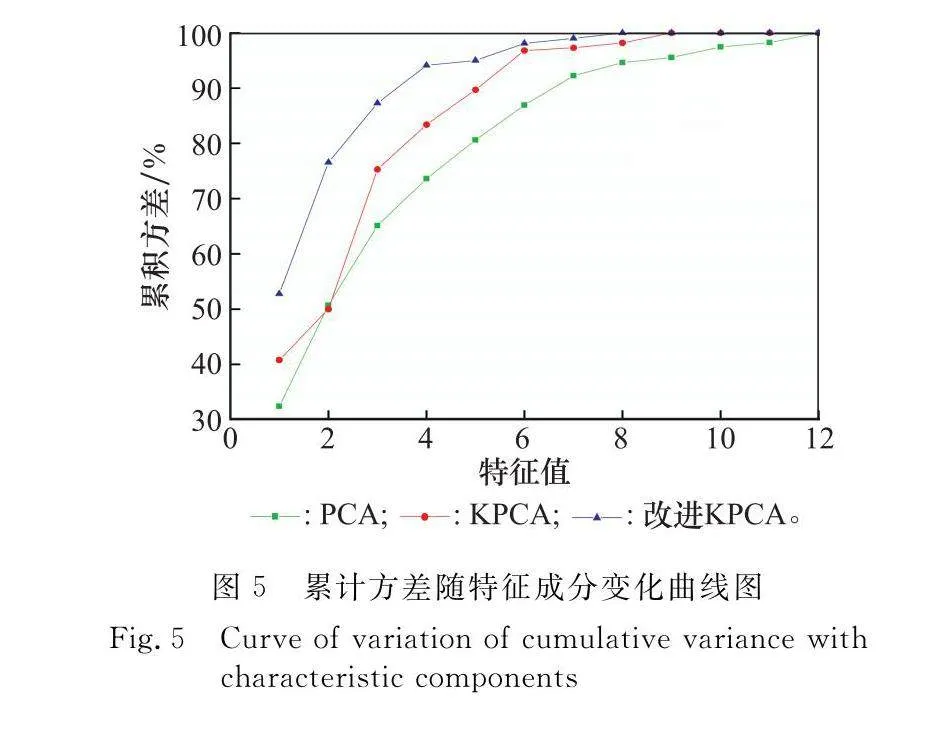
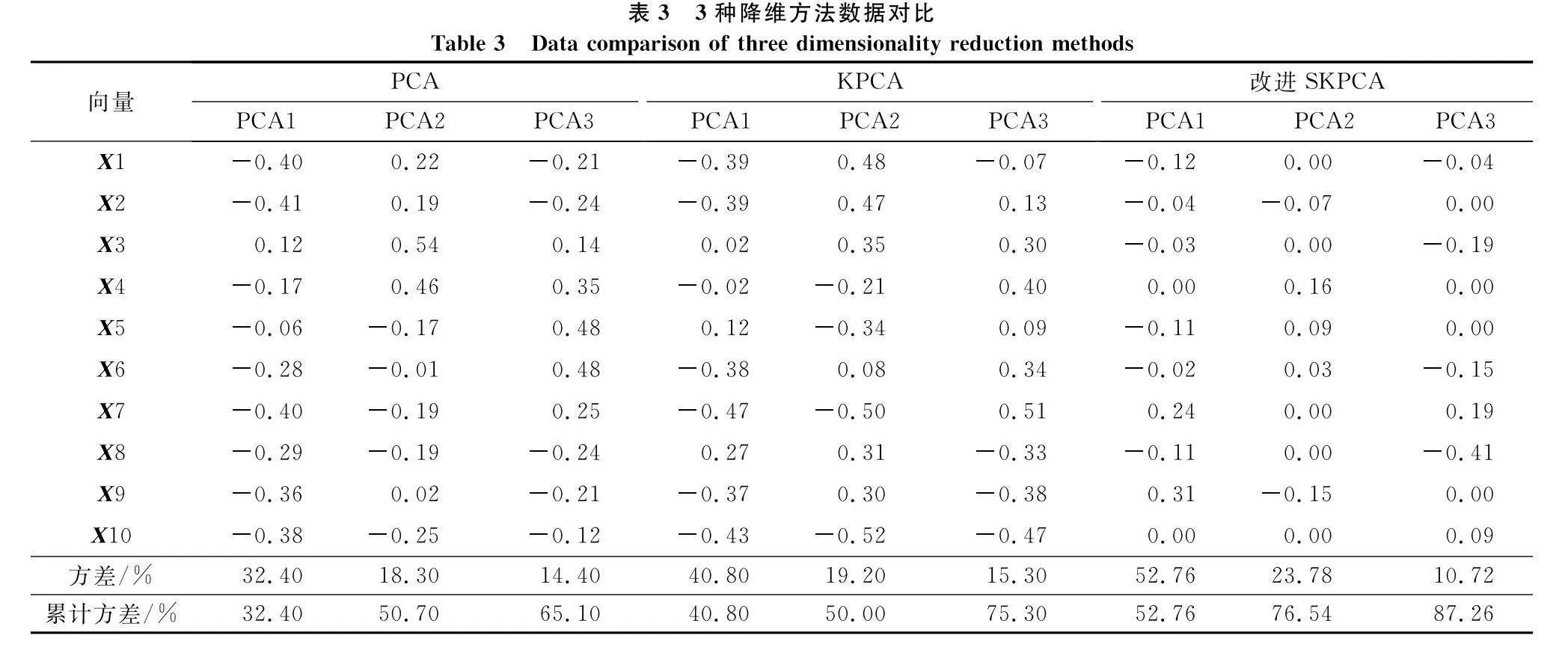
使用PCA、KPCA和改進的KPCA對多維器材數據進行特征降維并形成特征向量。采用高斯核徑向基函數（σ=100）對特征向量矩陣進行中心化處理，要求主成分累計方差貢獻率不低于95%。因篇幅受限，隨機選取所得實驗中10組數據（X1～X10）進行分析，使用3種降維方法后10組特征向量及主成分方差貢獻如表3所示（截取前三主成分）、累積方差隨特征成分變化曲線如圖5所示。

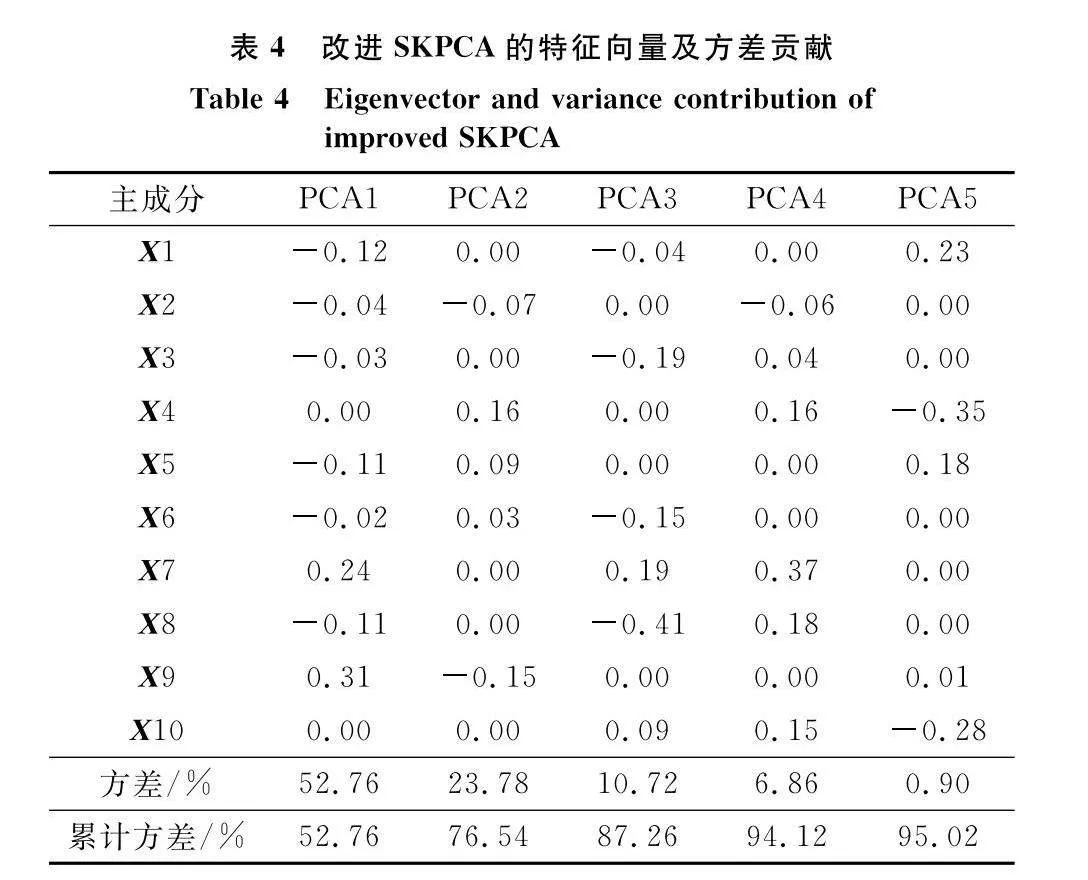
對照上述圖表，可以看出原始包含有12個主成分的10組特征向量，經過3種降維算法后均可有效提取主要特征指標，來達到維數約簡的目的，但因改進的SKPCA算法（具體數據見表4）集成了其他兩種算法的優勢，在數據降維、累積解釋方差、計算時間和復雜度上均展現了較好的性能，這里重點從主成分結構的信息含量和可解釋性兩方面總結其優越性：

（1） 改進的SKPCA主成分方差貢獻率更為集中，可有效甄別主成分信息特性。表3中PCA和KPCA的第1主成分方差貢獻率分別為32.4%和40.8%，體現少量信息的指標（如方差貢獻率小于1%的主成分）基本沒有，而改進的SKPCA第1主成分方差貢獻率已提高至52.76%，小于1%的主成分存在1個，說明改進的SKPCA可有效提取主成分，在相同方差貢獻率條件下所需主成分個數較少，同時可以有效篩選主成分信息含量，有利于縮減數據容量、實現數據降維。

（2） 改進的SKPCA主成分結構更具解釋性，突出了主成分變量的稀疏性。表3中PCA和KPCA的特征向量矩陣中基本不存在零系數，從向量表達上很難解析主成分的構成，所有因素都要考慮進來，但表4中改進的SKPCA每個向量都存在兩個或更多的零系數，可有效刪除零值影響因素，僅保留代表較大信息的重要影響因素，使特征向量能用較少的主成分來表達，增強了主成分變量的稀疏性，主成分結構更具解釋性。

4.2.2 預測模型對比

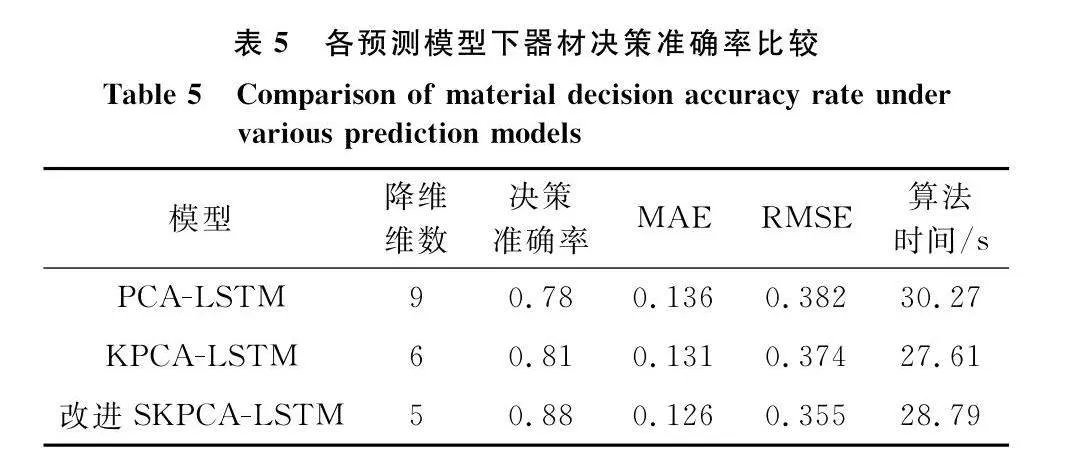
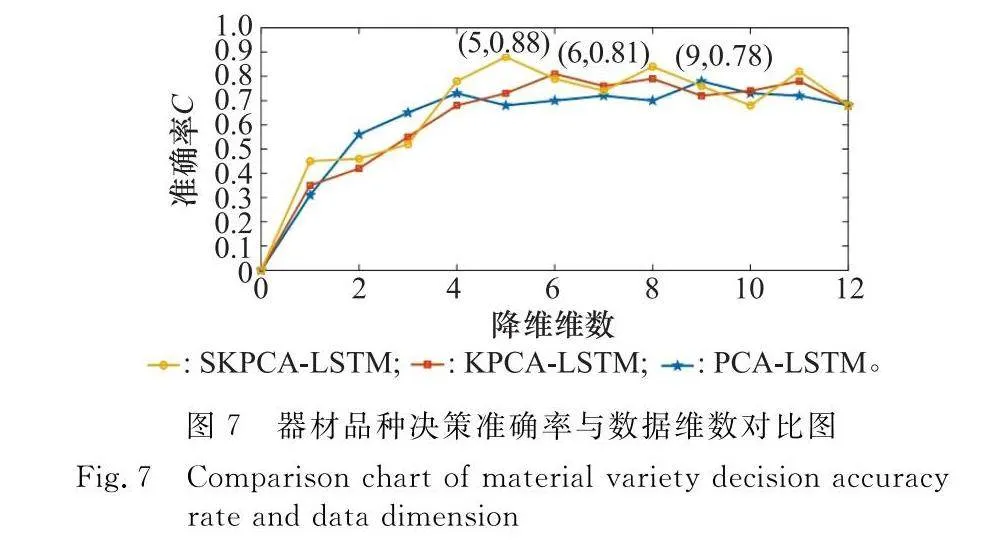
為達到95%以上的累計方差貢獻率閾值，改進的SKPCA保留了5個主成分作為LSTM神經網絡的輸入，有效解決了因攜行器材品種多維屬性造成的輸入數據規模大、運算時間長的問題。經初步測試，由混沌FPA（設定其轉換概率為0.8，步長縮放因子為1.5）迭代優化出LSTM的超參數，最終確定神經網絡隱含層數為2，隱含層神經元數為68和80，學習率為0.017 5，3種模型預測結果如圖6所示，誤差分析對比如表5所示，器材品種決策準確率與數據維數對比如圖7所示。

對比上述圖表，可以從不同側面反映預測模型在數據質量、模型準確性等方面的適用性和實用價值，具體分析如下：

（1） 分析表5可知，不同降維方法處理后LSTM運行時間相差不大，預測模型的決策準確率有所提高，攜行結果更加接近實際值。相對PCA-LSTM和KPCA-LSTM而言，改進的SKPCA-LSTM的MAE精度分別提高了7.3%和3.8%，誤差波動范圍RMSE精度也提高了6.9%和5.3%，改進的預測模型有效實現了數據的特征降維，提高了輸入數據質量，最終提升了預測模型的精準度。

（2） 分析器材品種決策準確率與數據維數對比圖（見圖7）：3種降維算法一開始隨著維數的增加，器材品種決策準確率逐漸升高，當準確率升至最大值時達到算法最優降維維度。之后伴隨維數繼續增加，器材品種決策準確率出現一定的下降并最終趨于穩定，這是因為當降維維數為全部因素時，等同于沒有降維，原始數據特征指標中因存在大量冗余或無用信息，對數據決策結果產生干擾，所以在預測模型開始前對原始輸入數據進行降維處理很有必要。相比之下，改進的SKPCA降維法的器材品種決策準確率最高，當降維維數為5時，準確率達到了0.88，KPCA降維法次之，這是因為改進的SKPCA能夠處理非線性數據，同時在KPCA算法基礎上融合了SPCA彈性懲罰修正特點，簡化了主成分結構，增強了主成分變量的稀疏性，保留了重要信息的影響因素，較好反映了非線性數據之間的流形結構^［25］;PAC降維算法得到的決策準確率最低，盡管保留了9維數據成分，但因其主要通過線性變換將高維數據轉化為低維數據，在映射空間轉換時造成了數據間非線性關系缺失，最終得到的器材品種決策準確率較低。

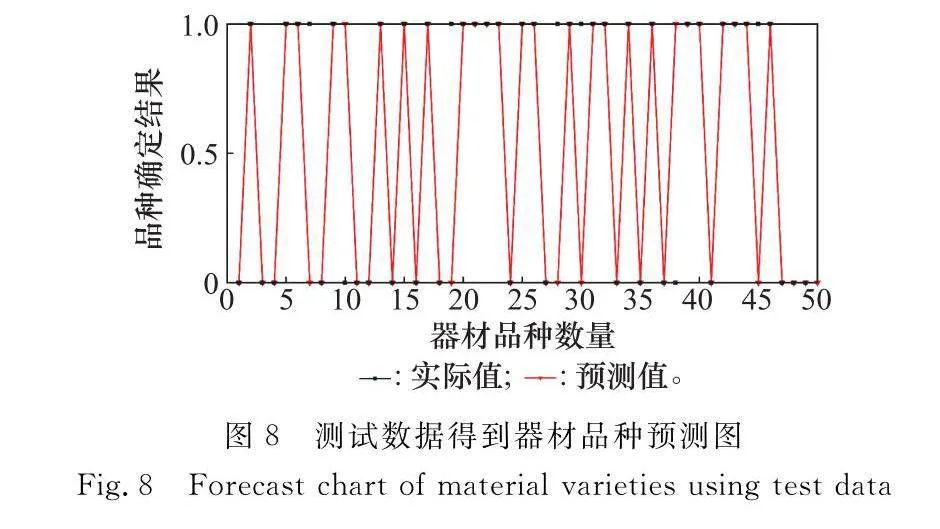
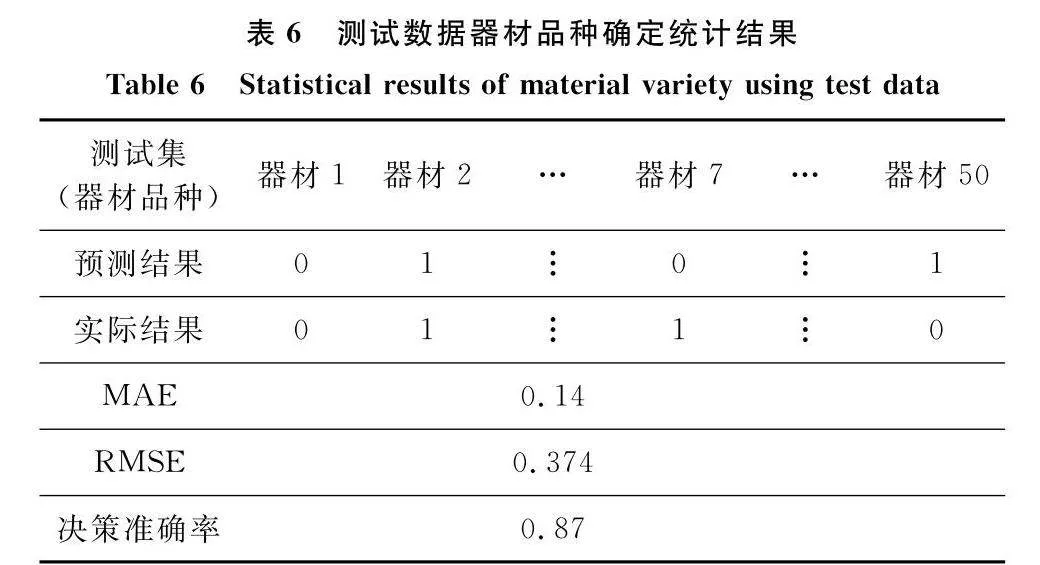
為驗證預測模型的預測效果，將訓練所得LSTM模型應用于另外50組測試樣本進行測試，攜行器材品種確定結果如圖8和表6所示。

上述圖表說明，本文模型在該階段任務數據下對器材品種確定具有較好的決策準確率，改進的SKPCA-LSTM預測模型可以為指揮員提供下一階段任務或相似階段任務可能需要的攜行器材品種清單提供一定的方法借鑒;但該模型方法也有其局限性，比較適用于器材消耗規律較為平穩、數據量較大、數據變化具有時序性的情形。本算例數據來源于遂行演習任務中典型階段任務——機動階段中裝備底盤系統相關部件的使用數據，該階段任務裝備故障多、器材消耗大、數據量較大，因此算例分析所得模型結果較好、決策準確率相對較高;其他系統部件如上裝身管，在整個演習過程中火炮射擊發數較少，該部件故障數據少，隨階段任務裝備動用和頻次的不同，不同階段任務呈現出特殊性，器材消耗規律差異較大，模型準確性會大受影響;另外該預測模型的準確性還依賴于階段任務之間的關聯性和數據來源的相似性，比如未來任務和以前歷史任務的相似性，器材消耗規律的連續性是否存在，這一點是該模型方法得到較好準確率的核心所在。鑒于此，本文所提預測方法和數據來源、階段任務相似性密切相關，數據量受階段任務、裝備狀態、訓練時長等因素綜合影響，模型的決策準確性有所變化，模型的普適性和實用性還有待增強。

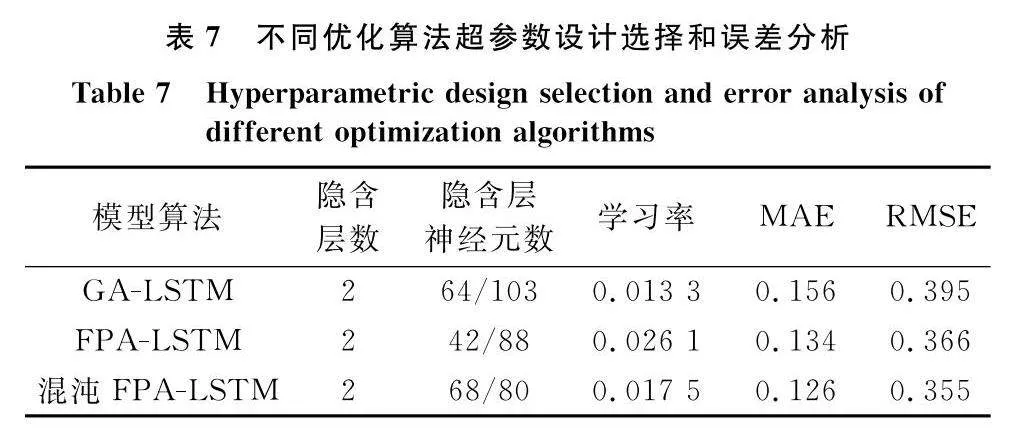
4.3 超參數優化分析

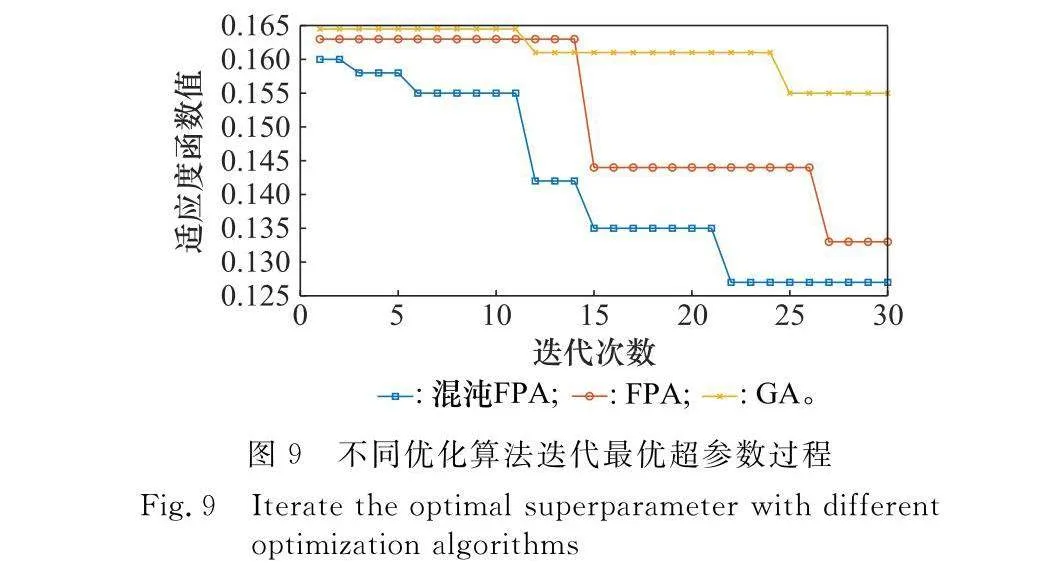
本文采用遺傳算法（genetiv algorithm， GA）、FPA和混沌FPA分別優化LSTM神經網絡隱含層數、隱含層神經元數和學習率3個參數（見表7），混沌FPA優化LSTM網絡結構參數后，所得預測模型的MAE相比其他兩類模型算法分別提高了5.9%和19.2%，RMSE分別提高了3%和10.1%。優化算法及迭代收斂性能對比如圖9，可以看出3種智能算法的初始種群適應度值基本一致，但找到的適應度最低值卻各有不同。GA的尋優效果和收斂性都較其他方法偏弱，而混沌FPA繼承了傳統FPA參數少、尋優快、不易早熟的特點，并從種群的多樣性角度增強花粉粒子的遍歷性，避免了過早陷入局部收斂的局面，尋優過程下降梯度大。可見，改進后的LSTM預測模型在收斂性、尋優速度和效果上都有一定的提升。

4.4 綜合對比分析

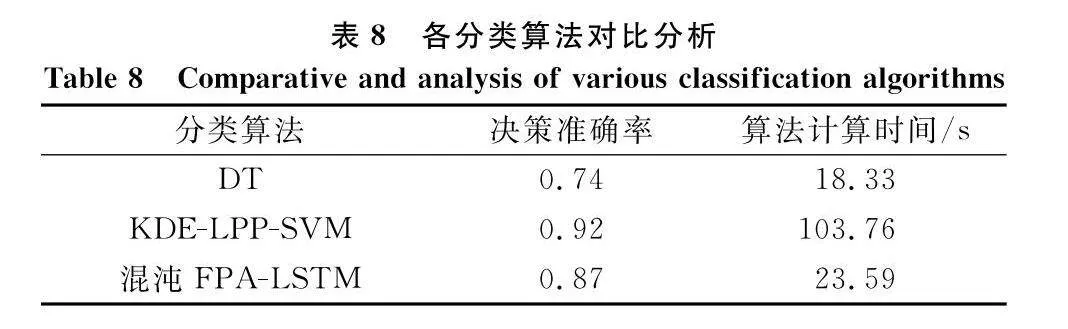
為進一步探索本文方法與以往研究成果的對比分析，這里將測試用例數據輸入至文獻［31］提出的基于核密度估計的局部保持投影（KDE-LPP）-SVM分類優化算法和傳統決策樹（decision tree， DT）分類算法進行效果對比，如表8所示：DT作為傳統分類方法，其原理易于理解、幾乎不需要數據的預處理，屬于典型的有監督學習，時間效率較快，但生成的樹結構如果過于復雜，則容易帶來數據的過擬合，降低預測的精度;從模型決策準確率來看，文獻［31］所提模型分類決策效果較優，這是因為KDE-LPP-SVM分類優化算法本質上是從特征提取角度創造出新的特征向量并重構高維數據空間，最大程度地還原了原始數據指標特性，較大可能地保留了局部結構特征，提升了器材品種決策的準確性，但由此帶來的時間復雜性成本較大，運算效率相對較慢。所以從算法效率上來看，本文方法提升幅度較大，主要是因為本文模型從特征選擇的角度進行SKPCA，增強特征指標的可解釋性，可有效反映數據本質，突出數據消耗規律;同時采用LSTM智能算法兼顧考慮了階段任務數據的時序關聯性，從整體上降低了時間復雜性，有效縮短了訓練時間，即便在數據不足的情況下對數據進行預處理，該預測模型同樣具有一定的預測精準性、對系統邏輯性要求較低，可為戰時指揮人員快速開展攜行器材輔助決策給予一定的方法指導。

5 結束語

針對執行階段任務武器裝備維修器材品種多、影響因素雜且關聯關系不明確造成的攜行器材品種確定困難的現實問題，提出了一種將改進SKPCA算法與LSTM模型相結合的階段任務攜行器材品種確定方法。在分析具有任務階段時序相關的攜行器材影響因素及特征指標的基礎上，運用基于彈性懲罰的SKPCA降維算法，對器材特征進行降維分析并得到低維稀疏特征向量，從而縮減了數據容量，最大程度地保證了原始數據主成分結構的信息含量和可解釋性，提高了輸入數據的質量效益;考慮到階段任務間器材消耗具有時序相關性，將最優降維約簡特征向量輸入LSTM預測模型，運用混沌序列改進FPA優化LSTM超參數，構建混沌FPA-LSTM預測模型，從而實現了攜行器材品種的科學確定。最后通過對演習攜行器材品種確定算例分析驗證了方法的科學性和可行性。下一步應著眼預測模型在普適性和實用性等方面的不足，加強對于數據管理的相關建議，比如數據獲取、數據分析等數據預處理、預清洗相關技術，作為未來模型輸入的重要考慮問題。

參考文獻

［1］阮旻智， 傅健， 周亮， 等. 面向任務的作戰單元攜行備件配置優化方法研究［J］. 兵工學報， 2017， 38（6）： 1178-1185.

RUAN M Z， FU J， ZHOU L， et al. Configuration and opimization method of carrying spares of mission-oriented combat unit［J］. Acta Armamentarii， 2017， 38（6）： 1178-1185.

［2］FRANDSEN C S， NIELSEN M M， CHAUDHURI A， et al. In search for classification and selection of spare parts suitable for additive manufacturing： a literature review［J］. International Journal of Production Research， 2020， 58（4）： 970-996.

［3］呂金建， 賈長治， 楊建春. 基于模糊綜合評判法的裝備備件應急制造性評價［J］. 火炮發射與控制學報， 2018（1）： 82-86， 91.

LYU J J， JIA C Z， YANG J C. Emergency manufacturing evaluation of equipment spare parts based on fuzzy comprehensive evaluation method［J］. Journal of Gun Launch ＆ Control， 2018（1）： 82-86， 91.

［4］蘇小波. 陸軍合成旅戰時裝備維修保障籌劃建研究［D］. 石家莊： 陸軍工程大學， 2021.

SU X B. Research on the planning and establishment of wartime equipment maintenance support for the army’s composite brigade［D］. Shijiazhuang： Army Engineering University Shijiazhuang Campus， 2021.

［5］PRACHUABSUPAKIJ W. ABC classification in spare parts for inventory management using ensemble techniques［C］∥Proc.of the IEEE Asia Pacific Conference on Circuits and Systems， 2019： 333-336.

［6］肖麗麗， 靳峰雷， 谷繼品. 控制棒驅動機構備件數量優化方法［J］. 原子能科學技術， 2020， 54（7）： 1273-1278.

XIAO L L， JIN F L， GU J P. Opitimization method for spare part quantity of control rod drive mechanism［J］. Atomic Energy Science and Technology， 2020， 54（7）： 1273-1278.

［7］SHEIKH-ZADEH A， SCOTT M A， ENAYATY-AHANGAR F. The role of prescriptive data and non-linear dimension-reduction methods in spare part classification［J］. Computers amp; Industrial Engineering， 2023， 175（8）： 1089-1102.

［8］ZHANG X L， TAN Y J， YANG Z W. Resource allocation optimization of equipment development task based on MOPSO algorithm［J］. Journal of Systems Engineering and Electronics， 2019， 30（6）： 1132-1143.

［9］季嘉偉， 孫國文， 羅佳偉. 基于模糊綜合評判的電源車戰場搶修備件品種研究［J］. 裝備制造技術， 2017（7）： 214-216.

JI J W， SUN G W， LUO J W. Fuzzy comprehensive evaluation of BDAR spare parts varieties of aircraft power vehicle［J］. Equipment Manufacturing Technology， 2017（7）： 214-216.

［10］楊超， 侯興明， 陳小衛， 等. 新型小規模裝備備件品種確定的猶豫模糊粗糙集決策方法［J］. 國防科技大學學報， 2022， 44（3）： 201-210.

YAHG C， HOU X M， CHEN X W， et al. Hesitant fuzzy rough set decision-making method for determining spare parts variety of nem small-scale equipment［J］. Journal of National University of Defense， 2022， 44（3）： 201-210.

［11］趙力， 史賢俊， 張志龍. 基于AHP和灰色局勢決策模型的裝備測試資源選擇和優化配置［J］. 導航定位與授時， 2022（3）： 92-99.

ZHAO L， SHI X J， ZAHNG Z L. Method of resourse selection and optimal allocetion based on AHP and Grey situation decision model［J］. Navigation Positioning amp; Timing， 2022（3）： 92-99.

［12］楊超， 侯興明， 秦海峰， 等. 基于限制優勢關系的航天裝備備件品種確定［J］. 系統工程與電子技術， 2022， 44（2）： 584-591.

YANG C， HOU X M， QIN H F， et al. Variety determination of spare parts for space equipmeng based on the relationship of limitied advantages［J］. Systems Engineering and Electronics， 2022， 44（2）： 584-591.

［13］于曉琳， 張磊， 楊奕飛， 等. 基于改進優劣解距離法和價值工程的艦船備件配置［J］. 科學技術與工程， 2021， 21（30）： 13170-13176.

YU X L， ZHANG L， YANG Y F， et al. Warship spare parts allocation based on improved technique for order preference by similarity to ideal solution and value engineering［J］. Science Technology and Engineering， 2021， 21（30）： 13170-13176.

［14］楊帆， 王生鳳， 王鐵寧， 等. 基于全過程的備件需求預測綜述［J］. 裝甲兵工程學院學報， 2018， 32（3）： 25-29.

YANG F， WANG S F， WANG T N， et al. Review on spare parts forecasting based on whole process management［J］. Journal of Armored Forces， 2018， 32（3）： 25-29.

［15］林琳， 陳湘芝， 鐘詩勝. 基于特征合成的周期性備件需求預測方法［J］. 哈爾濱工業大學學報， 2016， 48（7）： 27-32.

LIN L， CHEN X Z， ZHONG S S. Demand forecasting method for periodic spare parts based on feature synthesis［J］. Journal of Harbin Institute of Technology， 2016， 48（7）： 27-32.

［16］CAO W B， SONG W Y， HAN Y C， et al. Spare parts demand forecasting： a review［J］. Journal of Donghua University （English Edition）， 2016， 33（2）： 340-344.

［17］PINCE C， TURRINI L， MEISSNER J. Intermittent demand forecasting for spare parts： a critical review［J］. Omega， 2021， 105（7）： 102513-102535.

［18］RATNAYAKE R M C. Consequence classification based spare parts evaluation and control in the petroleum industry［C］∥Proc.of the IEEE International Conference on Industrial Engineering and Engineering Management， 2019： 1204-1210.

［19］CAO L J， CHUA K S， CHONG W K， et al. A comparison of PCA， KPCA and ICA for dimensionality reduction in support vector machine［J］. Neurocomputing， 2003， 55（1/2）： 321-336.

［20］張明藍， 孫林夫， 鄒益勝. 基于深度網絡的汽車配件兩級備件決策［J］. 計算機集成制造系統， 2019， 11（31）： 2238-2246.

ZHANG M L， SUN L F， ZOU Y S. Two-level spare parts decision for auto parts based on deep network［J］. Computer Integrated Manufacturing Systems， 2019， 11（31）： 2238-2246.

［21］MEMARZADEH G， KEYNIA F. Short-term electricity load and price forecasting by a new optimal LSTM-NN based prediction algorithm［J］. Electric Power Systems Research， 2021， 192（10）： 106995-107016.

［22］王雷. 裝備戰場搶修時間計劃研究［D］. 長沙： 國防科學技術大學， 2010.

WANG L. Equipment battlefield emergency repair time planning study［D］. Changsha： National University of Defense Technology， 2010.

［23］STOLL J， KOPF R， SCHNEIDER J， et al. Criticality analysis of spare parts management： a multi-criteria classification regarding a cross-plant central warehouse strategy［J］. Production Engineering， 2015， 9（2）： 225-235.

［24］SUN Y， WEI Q， ZHUANG Z L， et al. An adaptive fault detection and root-cause analysis scheme for complex industrial processes using moving window KPCA and information geometric causal inference［J］. Journal of Intelligent Manufacturing， 2021， 32（7）： 2007-2021.

［25］杜春， 孫即祥， 周石琳， 等. 基于稀疏表示和非參數判別分析的降維算法［J］. 國防科技大學學報， 2013， 35（2）： 143-147.

DU C， SUN J X， ZHOU S L， et al. Dimensionality reduction based on sparse representation and nonparametric discriminant analysis［J］. Journal of Nonal University of Defense Technology， 2013， 35（2）： 143-147.

［26］TIPPING M E. Sparse kernel principal component analysis［C］∥Proc.of the Advances in Neural Information Processing Systems 13， Papers from Neural Information Processing Systems， 2000.

［27］王雙川， 賈希勝， 胡起偉， 等. 合成部隊多階段作戰任務成功概率仿真評估［J］. 系統工程與電子技術， 2021， 43（3）： 763-772.

WANG S C， JIA X S， HU Q W， et al. Success probability simulation evaluation of phased combat mission of the synthetic force［J］. Systems Engineering and Electronics， 2021， 43（3）： 763-772.

［28］YANG X S. Flower pollination algorithm for global optimization［C］∥Proc.of the International Conference on Unconventional Computing and Natural Computation， 2012.

［29］肖輝輝， 萬常選. 基于多策略的改進花授粉算法［J］. 軟件學報， 2021， 32（10）： 3152-3175.

XIAO H H， WANG C X. Improved flower pollination algorithm based on muilti-strategy［J］. Journal of Software， 2021， 32（10）： 3152-3175.

［30］HUANG Y， LI J P， WANG P. Unusual phenomenon of optimizing the Griewank function with the increase of dimension［J］. Frontiers of Information Technology amp; Electronic Engineering， 2019， 20（10）： 45-62.

［31］王強， 賈希勝， 程中華， 等. 基于改進的局部保持投影的戰時備件分類［J］. 系統工程與電子技術， 2020， 42（1）： 133-140.

WANG Q， JIA X S， CHENG Z H， et al. Classification of spare parts based on improved local preserving projection in wartime［J］. Systems Engineering and Electronics， 2020， 42（1）： 133-140.

作者簡介

吳巍屹（1982—），女，副教授，博士，主要研究方向為維修保障資源優化配置、裝備保障指揮。

賈云獻（1963—），男，教授，博士研究生導師，博士，主要研究方向為維修保障資源優化配置、維修決策建模。

姜相爭（1984—），男，工程師，博士，主要研究方向為軍事裝備學。

史憲銘（1975—），男，副教授，碩士研究生導師，博士，主要研究方向為裝備保障理論與應用。

劉 潔（1981—），女，講師，博士，主要研究方向為軍事裝備學、裝備保障指揮。

劉 彬（1984—），男，講師，博士，主要研究方向為維修工程、軍事裝備學。

董恩志（1997—），男，博士研究生，主要研究方向為維修工程。

朱 曦（1997—），男，博士研究生，主要研究方向為維修工程、基于性能的保障。