混凝土柱澆筑過程中模板壓力的數(shù)值模擬

【摘" " 要】：針對自密實混凝土自下而上泵送澆筑過程中，模板壓力變化規(guī)律不明確的問題，對自密實混凝土自下而上填充柱模板的過程進行了數(shù)值模擬，通過與試驗數(shù)據(jù)對比驗證模擬的準確性，進而探究了柱模板澆筑過程中模板壓力的變化規(guī)律。

【關鍵詞】：計算流體動力學；模板壓力；自密實混凝土

【中圖分類號】：TU528 【文獻標志碼】：A 【文章編號】：1008-3197（2024）06-70-03

【DOI編碼】：10.3969/j.issn.1008-3197.2024.06.018

Numerical Simulation of Formwork Pressure While Pumping Self-Compacting Concrete Column

【Abstract】： In view of the variation law of formwork pressure is not clear when pumping self-compacting concrete from the bottom up. The filling process of column formwork with self-compacting concrete was numerically simulated. The accuracy of the numerical simulation was verified by comparing with the test data， and then the variation of formwork pressure during column formwork pouring was investigated.

【Key words】： CFD；formwork pressure； self-compacting concrete

目前，大多數(shù)確定模板壓力的規(guī)范[1]都是針對普通混凝土澆筑工藝制定的，有些不適用自密實混凝土的澆筑。普通混凝土是從模板頂部開始澆筑，通過采取分層且振動的方式使混凝土足夠密實，澆筑效率低。自密實混凝土具有良好的流動性與密實性[2～4]，可以連續(xù)澆筑各類模板，省去了分層與振搗過程，澆筑時間可顯著減少；但是相比于普通混凝土澆筑，自密實混凝土連續(xù)的澆筑方式使得模板承受混凝土施加的全部靜水壓力，對模板設計提出了更高要求。

自密實混凝土連續(xù)澆筑可分為兩種：從模板頂部澆筑和從模板底部泵送澆筑。從模板頂部澆筑的代表方法之一就是高拋振搗法[5～7]，這種方法增加了混凝土中空氣滯留和骨料砂漿分離的可能性。從模板底部泵送澆筑首先，避免或限制了自密實混凝土澆筑過程中空氣滯留的風險，有利于提高澆筑質(zhì)量；其次，混凝土持續(xù)向上運動，避免了混凝土離析的發(fā)生，有利于提高混凝土的強度；最后，可以提高澆筑效率，大大減少澆筑所需時間。然而，目前關于自密實混凝土自下而上澆筑模板的研究較少，對模板壓力的變化規(guī)律不明確。

本文以自密實混凝土自上而下澆筑柱模板的過程為研究對象，采用CFD軟件對自密實混凝土的澆筑過程進行數(shù)值模擬，以探明這一過程中模板壓力的變化規(guī)律，為模板設計提供參考。

1 模型驗證

1.1 數(shù)值模型建立

為驗證數(shù)值模擬的準確性，本文首先以文獻[8]中的自密實混凝土柱為模擬對象，柱的高、寬、深分別為2 000、174、210 mm，自密實混凝土從柱模板底部泵入，泵管的直徑為106 mm，泵管中心位置距模板底部的高度為270 mm，壓力測量儀距模板底部的高度為385 mm。

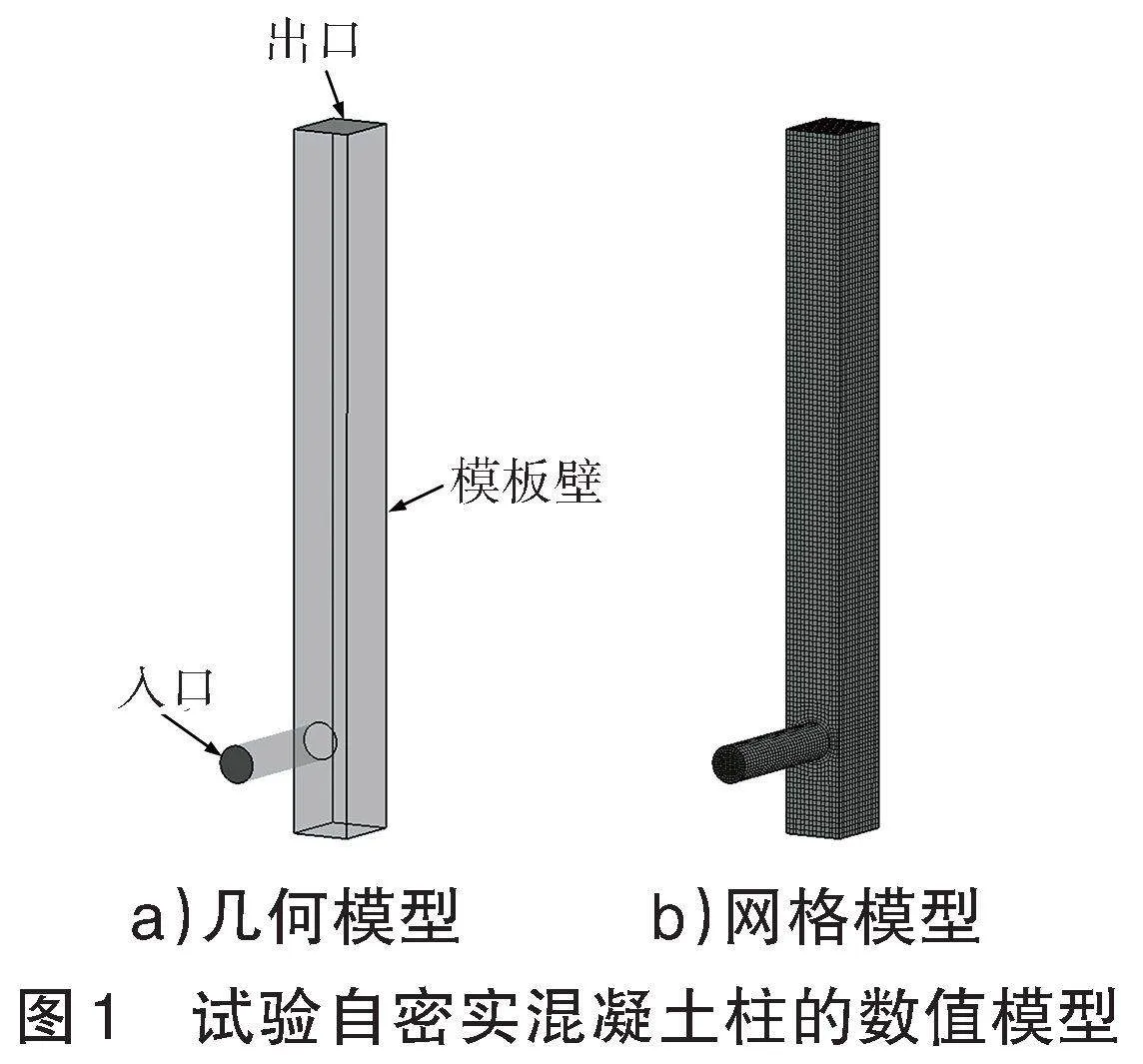
采用CFD軟件建立柱的數(shù)值模型并進行求解，見圖1。

為了捕捉模板澆筑過程中自密實混凝土和空氣之間界面的變化，采用VOF方法求解動量方程，即通過計算空氣和混凝土的體積分數(shù)來追蹤混凝土界面的變化。模型入口為速度型入口，設置于泵管進口端，入口速度大小為0.57 m/s；出口設置于模型頂部，表壓為0，允許空氣自由進出計算域；管壁和模板壁為無滑移壁面。自密實混凝土視為一種均質(zhì)非牛頓流體，通過Herschel-Bulkley模型定義其流變特性并假設混凝土的流動為層流，由于自密實混凝土具有良好的工作性能，因此忽略自密實混凝土的觸變性。

[τ=τ0+k?γn] （1）

式中：[τ]為剪切力，Pa；[τ0]為屈服應力，Pa；[k]為一致性指數(shù)，（Pa·sn）；[γ]為剪切速率，s-1； [n]為冪指數(shù)。

根據(jù)自密實混凝土工作試驗數(shù)據(jù)，自密實混凝土的密度為2 314 kg/m3，屈服應力[τ0]、一致性指數(shù)[k]和冪指數(shù)[n]分別為10.3 Pa、17.7 Pa·sn和1.35。

采用有限體積法對計算域進行離散化，動量方程求解器為雙精度隱式求解器，以保證計算精度。時間步長設置為0.01 s，時間步數(shù)為1 650，總時間為16.5 s。

1.2 模擬結果

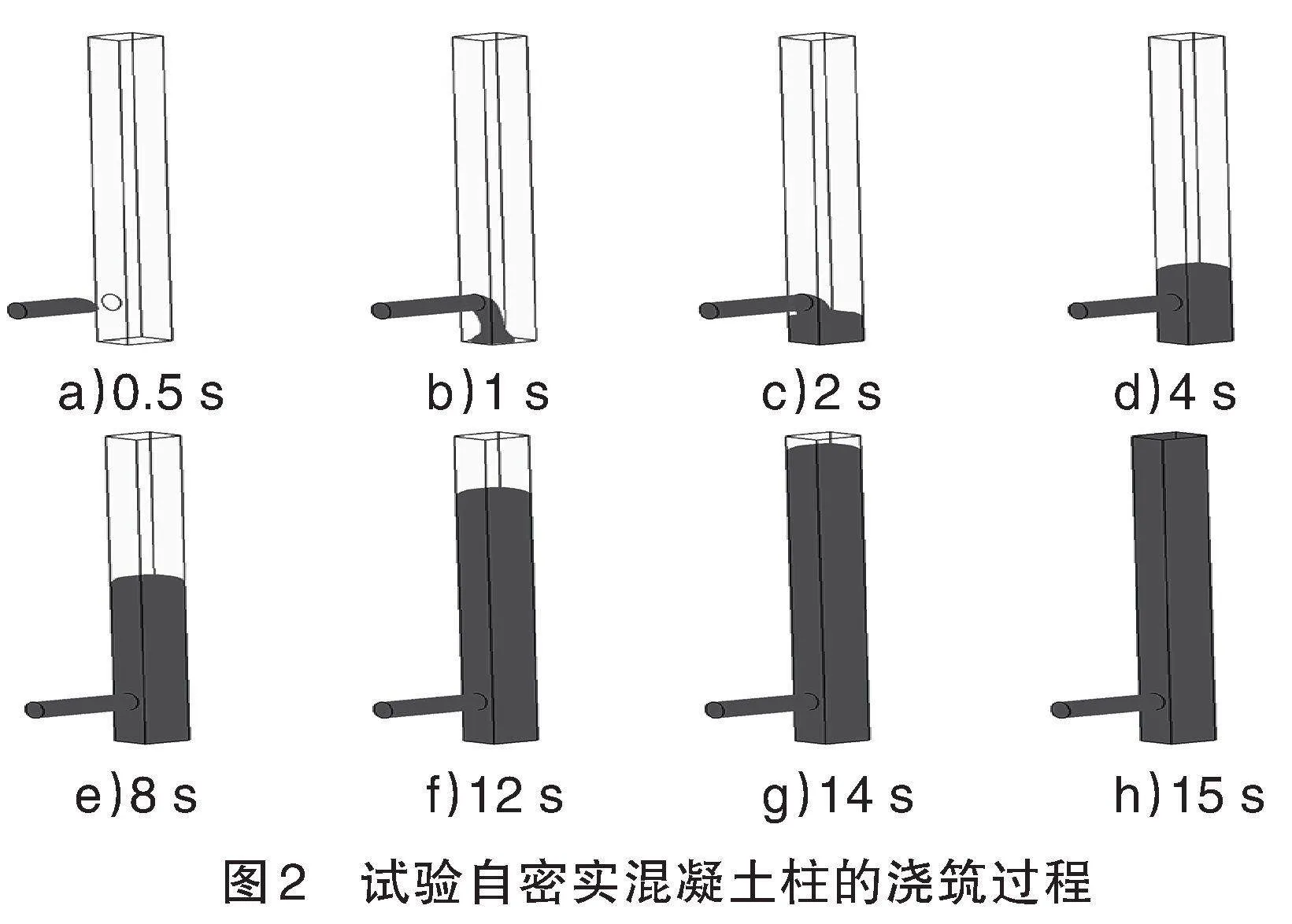
混凝土柱澆筑初始階段，混凝土表面出現(xiàn)了小坡度，隨著澆筑時間的增長，混凝土表面的坡度逐漸消失，這主要是由于混凝土的自流平特性。見圖2。

自密實混凝土柱澆筑過程的模擬證明了VOF法能夠準確捕捉到自密實混凝土與空氣界面隨時間的變化過程。

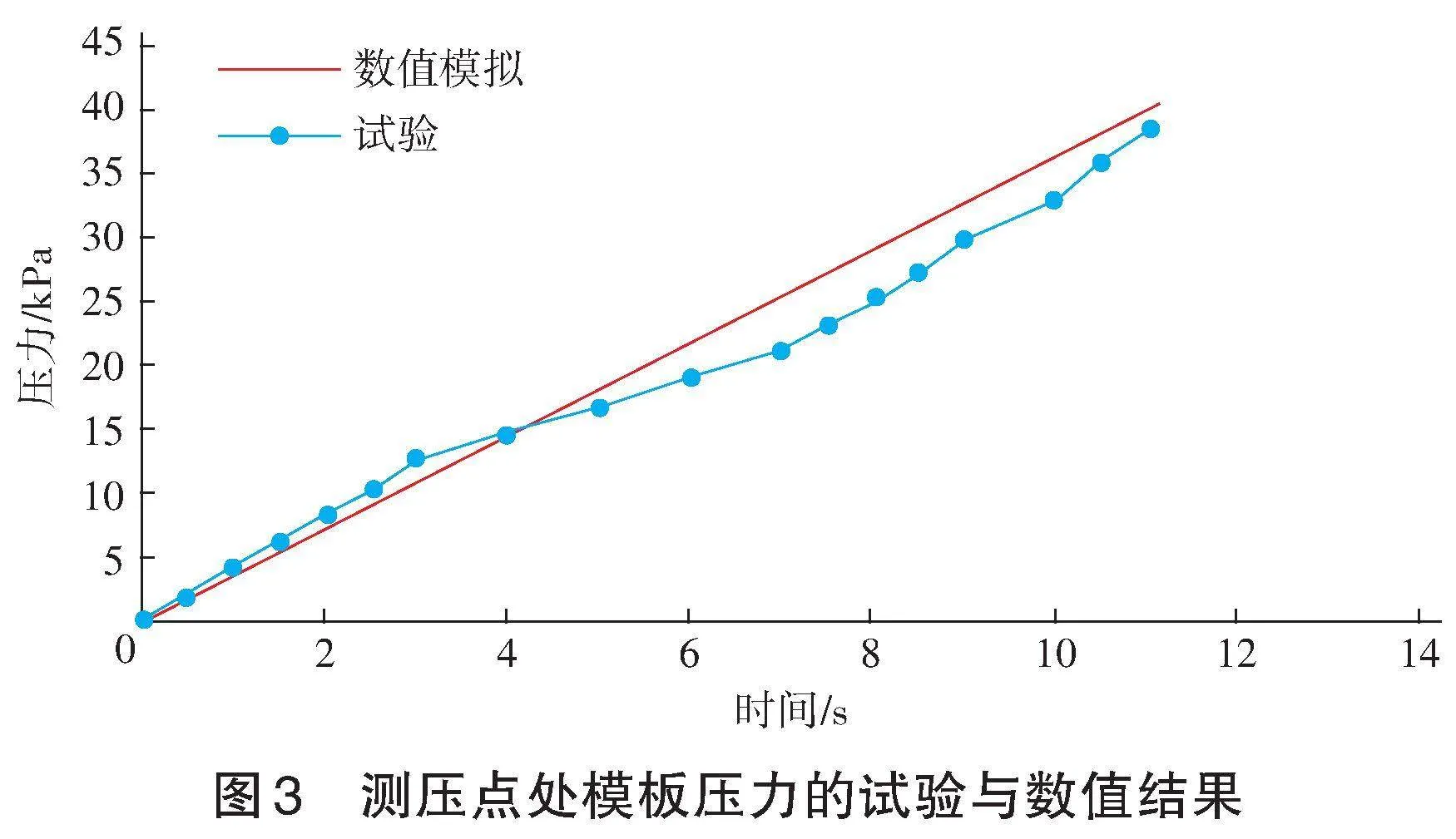
測量點處壓力值隨澆筑時間的增加近線性增長，試驗結果與模擬結果基本吻合，證明數(shù)值模型能夠較為準確地預測自密實混凝土模板澆筑過程中壓力的變化規(guī)律。見圖3。

試驗結果與模擬結果之間的差異性主要原因：首先，試驗模板在自密實混凝土的側向壓力下會發(fā)生微變形，導致試驗測試壓力值出現(xiàn)波動，而數(shù)值模擬中模板為壁面條件，不會發(fā)生變形；其次，儀器測量誤差和人工讀數(shù)誤差可能會導致結果的差異性；最后，模擬中混凝土被視為一種均質(zhì)流體，而混凝土實際上包含骨料，這一假設可能導致壓力差異性的出現(xiàn)。

2 工程案例

海南省三亞崖州區(qū)某實驗樓的自密實混凝土柱截面為正方形，邊長600 mm、高度3 000 mm，泵管直徑為150 mm，泵管中心位置距模板底部的高度為500 mm，泵送速度為0.9 m/s。

采用CFD軟件建立該工程自密實混凝土柱的數(shù)值模型，模型的材料屬性、邊界條件和求解設置與驗證試驗模一致，澆筑總時間為70.5 s。見圖4。

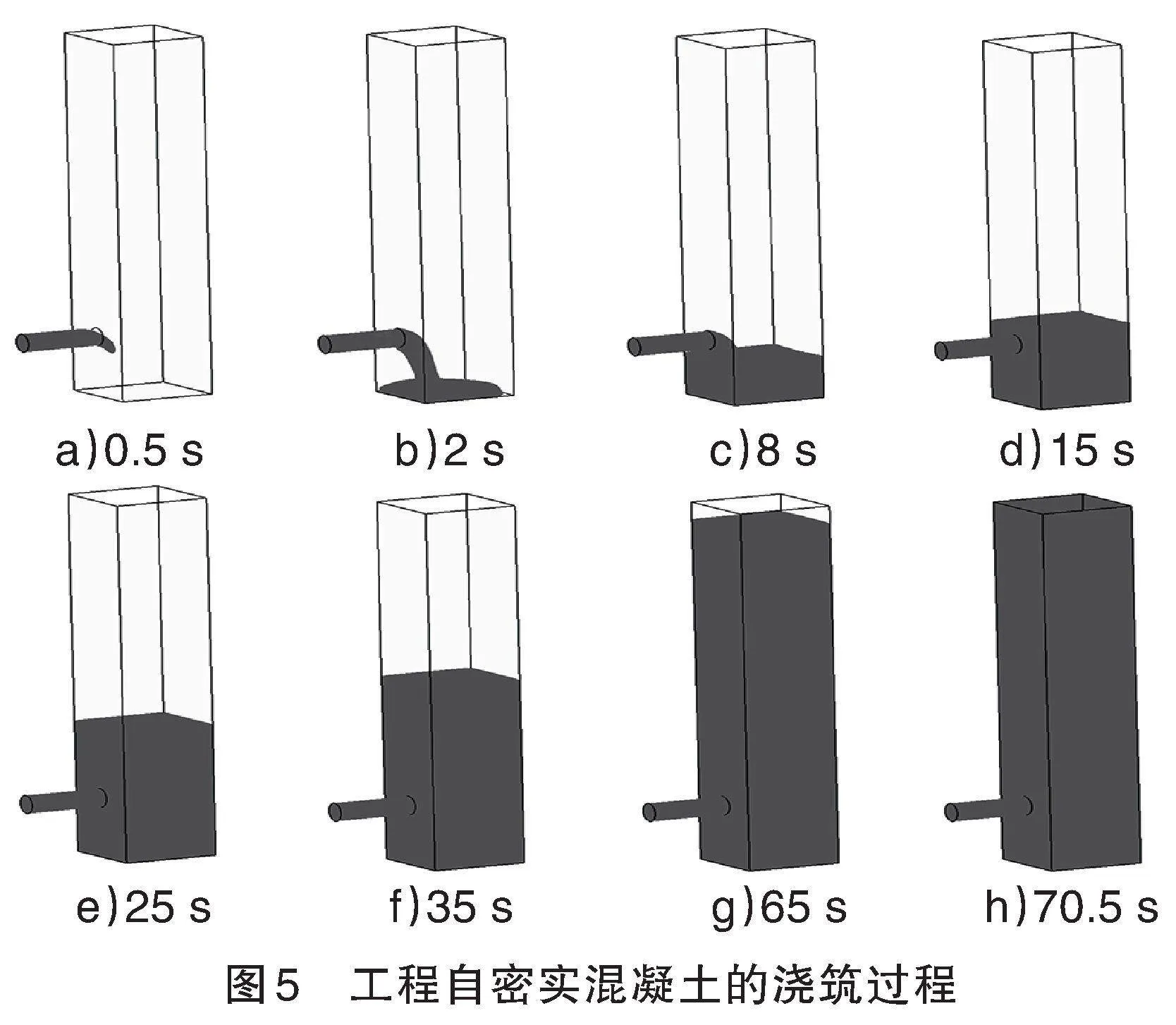
柱澆筑初始階段，混凝土表面亦出現(xiàn)了小坡度，而隨著澆筑時間的增長，混凝土表面的坡度逐漸消失，與試驗中觀察到的自密實混凝土現(xiàn)象相同。見圖5。

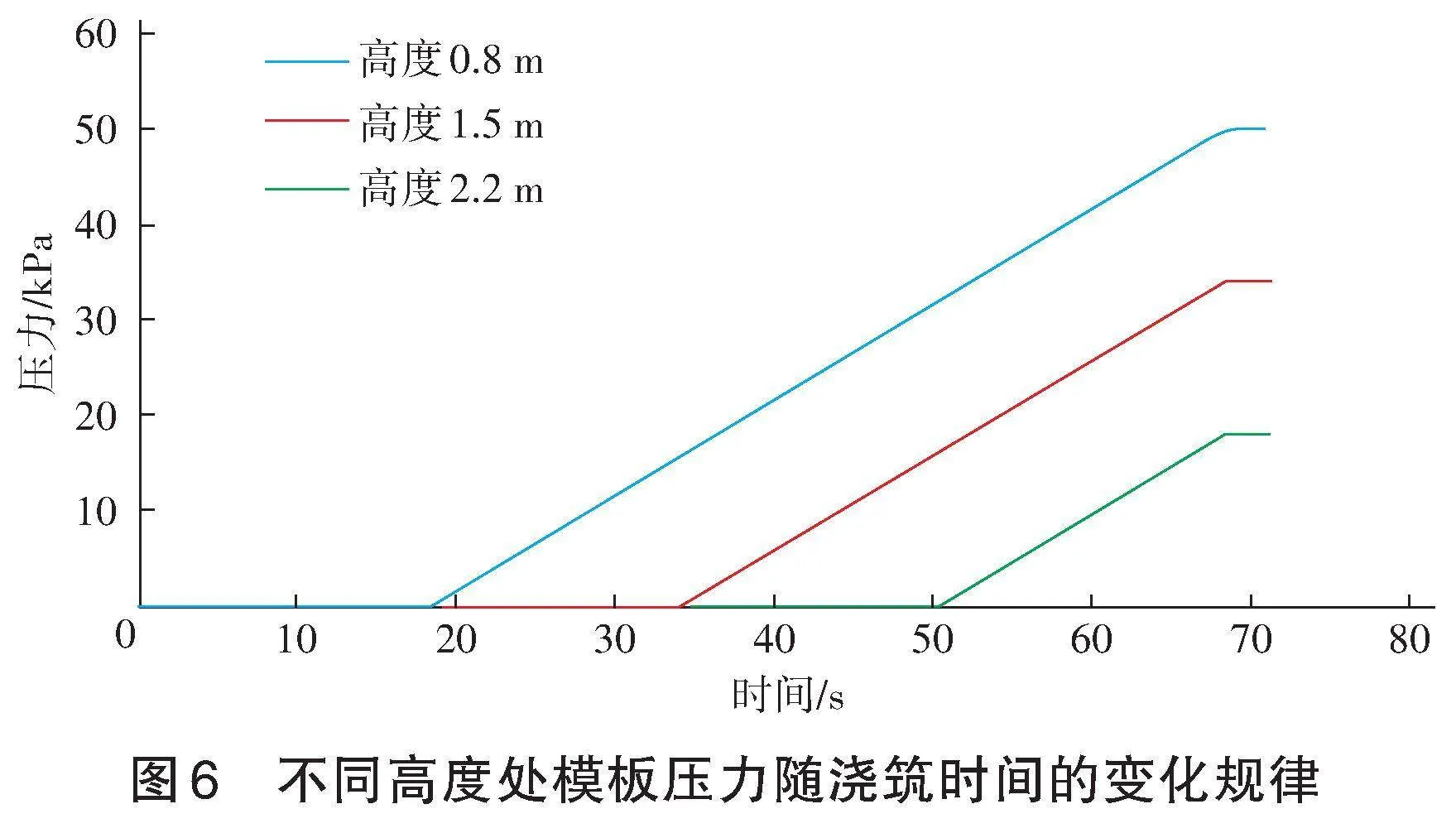
為分析自密實混凝土澆筑過程中不同位置處模板壓力的變化規(guī)律，選取澆筑口側0.2、0.8、1.5、2.2、2.9 m高度處的模板位置作為測壓點。不同高度處模板壓力增長的起始時刻不同，這是因為自密實混凝土液面達到測壓點高度所需時間不同，測壓點位置越高，液面達到該處的所需時間越久。不論測壓點高度為多少，當混凝土液面達到測壓點高度后，模板壓力均隨著澆筑時間的增加而線性增長，當澆筑時間達到70 s左右時，混凝土液面達到柱頂，液面高度不再上升，各測壓點處的壓力趨于穩(wěn)定。此外，模板壓力的最大值隨著測壓點高度的增加而減小，其中高度為0.8 m處的模板壓力值最大，為50.1 kPa。見圖6。

3 結論

1）數(shù)值模擬得到的壓力變化曲線與試驗結果基本吻合，說明建立的數(shù)值模型能夠較為準確地預測自密實混凝土填充模板過程中模板壓力的變化規(guī)律。

2）測壓點處模板壓力的數(shù)值隨著澆筑時間的增加而呈線性增長，數(shù)值結果與試驗結果的差異可以歸因于實際澆筑過程中模板的變形以及測量誤差。

3）不論測壓點高度為多少，各測壓點處模板壓力均隨著澆筑時間的增加而線性增長；模板壓力的最大值隨著測壓點高度的增加而減小。

參考文獻：

[1]中華人民共和國住房和城鄉(xiāng)建設部標準定額研究所. 混凝土結構工程施工規(guī)范：GB 50666—2011 [S] .北京：中國建筑工業(yè)出版社，2012.

[2]許" 博，李傳習，何" 穎. 雙摻粉煤灰和粉狀高爐礦渣的自密實混凝土流變性能的研究[J]. 混凝土，2022，（3）：160-163.

[3]王 "輝，馬嘉均，呂" 淼，等. 珠江三角洲水資源配置工程自密實混凝土配合比優(yōu)化設計試驗研究[J]. 水電能源科學，2021，39（29）：125-128.

[4]胡" 鵬，楊惠源，蘭宇鵬，等. 鋼渣橡膠自密實混凝土性能試驗研究[J]. 混凝土，2023，（9）：178-183.

[5]崔建軍，何彥琪，蔣" 震，等. 四摻法配制C60高拋自密實混凝土在礦坑修復工程中的應用[J]. 混凝土，2021，（5）：92-95.

[6]殷艷春，王" 寧，韓" 宇. 沈陽寶能環(huán)球金融中心C70大體積自密實混凝土關鍵制備技術與性能研究[J]. 混凝土，2019，（5）：138-141.

[7]高建民. 三摻法配制高拋免振搗混凝土在清水混凝土立柱中的研究[J]. 混凝土，2017， （4）：126-128.

[8]Serge Tichko， Jens Van De Maele， Niels Vanmassenhove， et al. Numerical simulation of formwork pressure while pumping self-compacting concrete bottom-up[J]. Engineering Structures， 2014，70（1）：218-233.