基于球形模糊和TOPSIS的鞋靴外觀方案決策方法

摘要： 針對鞋靴外觀方案決策的模糊性和復雜性問題，為獲得客觀合理的權重分配，文章提出基于球形模糊和TOPSIS的方案多屬性決策方法。從鞋靴的組成結構出發，確定用于決策鞋靴外觀方案的評價指標。利用球形模糊集將決策專家的評價語言轉換為定量信息，以描述決策情況并獲得評價指標的權重。同時，為避免決策專家的差異性對評價結果的影響，引入決策專家評價猶豫度以確定決策專家權重。綜合評價指標權重和決策專家權重，基于TOPSIS方法綜合表征決策方案間的相對重要性，通過分析備選方案與正負理想解之間的貼近度，實現鞋靴外觀方案的排序和擇優。以男式跑鞋的實例分析與方法對比驗證方法的合理性和可行性，研究結果表明，方法能夠綜合考慮決策專家的心理因素，評判不同鞋靴外觀方案的差異并做出有效決策。

關鍵詞： 球形模糊集;TOPSIS;權重;鞋靴;外觀;方案決策

中圖分類號： TS943.2

文獻標志碼： A

文章編號： 10017003（2024）12期數0043起始頁碼09篇頁數

DOI： 10.3969/j.issn.1001-7003.2024.12期數.004（篇序）

鞋靴作為面向消費者的產品，除實用的功能性外，也是體現個性風格和時尚意識的重要配飾。消費者對鞋靴產品的需求是多方面的，包括但不拘泥于良好的舒適性、可靠的功能性、價格的合理性及品牌的知名性等要素。隨著鞋靴產品主要屬性的轉變，消費者的購買決策因素已不再局限于舒適、耐穿與價廉，而是更多地傾向于鞋靴的設計個性化、象征價值及與需求的契合程度^［1］。為適應和滿足鞋靴升級的消費需求，鞋靴外觀設計的關鍵性日益凸顯，直接影響消費者的審美感受和購買欲望。

國內外學者從不同角度出發，推動鞋靴外觀領域的理論發展與實踐創新。李華^［2］針對鞋靴外觀藝術與用戶行為展開討論，分析消費者對鞋靴外觀藝術的需求。齊耐斌^［3］從實踐和理論兩個角度，探討時尚運動休閑鞋設計過程中應遵循的原則及要點。趙堅等^［4］結合情感化設計理念，研究仿生外觀在鞋靴設計中的應用。Spurrier等^［5］探討哺乳動物的足部形態與運動類型的相關性，為仿生攀巖鞋的設計提供參考。Xu等^［6］將感性工學應用至皮革鞋類產品的色彩和質感分析，通過神經網絡將消費者的視覺和觸覺意象映射于不同種類的皮革。該類研究大多側重于鞋靴外觀的分析和設計，包括用戶體驗與藝術審美、設計原則與理念創新，以及具體造型方案與色彩材質應用。鞋靴產品創新設計的實施通常涵蓋4個關鍵步驟：首先是市場調研與需求分析;其次是創新構思與概念設計;再次是方案評價與可行分析;最后是試生產與市場推廣。鞋靴外觀方案的評價是創新設計過程中的核心環節之一，然而現有研究對此環節的關注度相對較低。目前鞋靴方案的評價主要集中于鞋靴感知舒適性^［7-8］，較少涉及設計要素的美學價值。科學的鞋靴外觀方案評價方法不僅可以評估不同鞋靴設計方案的外觀特性，而且能有效反映消費者的需求和偏好，進而為鞋靴產品的研發提供指導和參考。

鞋靴外觀方案的評價過程可視為多屬性決策問題，存在不確定性信息而導致最優方案可能并不唯一，因此消除評價信息的模糊性對方案選擇產生的不利影響是多屬性決策研究的重點。裴卉寧等^［9］基于單值中智集和云模型聚類，解決復雜模糊情況下的汽車造型設計多屬性決策問題。楊延璞等^［10］綜合考慮產品造型設計多階段決策信息，提出引入復雜網絡理論的產品造型設計多階段網絡耦合決策流程。Shieh等^［11］以多重情感反應為背景，設計多目標優化和多準則決策的產品形態決策模型。Mao等^［12］將語言Z數與基于平均解距離法相結合提出新的QFD法，以共享汽車為例驗證方法的可靠性。該類決策方法為鞋靴外觀方案的決策提供了有效的參考，但是評價鞋靴外觀方案時仍然需要注意以下難點：一方面，鞋靴外觀特征的評價具有語言評價和模糊評價的不確定性，難以通過精確的數值對鞋靴的外觀特征進行量化。另一方面，鞋靴外觀方案的決策專家具有異質性，其專業背景、知識經驗、情緒感知和評價標準均存在差異。該異質性導致方案評價的過程中存在猶豫性和主觀性，進而增加達成共識的難度。

模糊集及模糊集理論通過定義隸屬度函數刻畫事物潛在的模糊性以表征不確定性評價信息^［13］。隨著研究的深入及決策環境復雜性的提升，模糊集已被拓展為多種形式，如直覺模糊集^［14］、猶豫模糊集^［15］、畢達哥拉斯模糊集^［16］和球形模糊集^［17］等。其中，Mahmood等^［17］提出的球形模糊集給予決策者更大的決策空間以客觀地反映決策者的真實表達，適合在實際問題中描述不確定性，以深入地反映事物的模糊性。由此可見，模糊集理論與鞋靴外觀方案的評價問題具有很高的契合度。除鞋靴外觀屬性的模糊性外，鞋靴外觀方案的決策過程還涉及方案的綜合排序問題。常用的解決方法包括灰色關聯分析、層次分析法和逼近理想解排序法（Technique for Order Preference by Similarity to an Ideal Solution，TOPSIS）等。TOPSIS的核心思想是根據評價指標與正負理想解的接近程度對決策方案進行排序，對樣本資料無特殊的要求，能夠充分運用原始數據的信息，可避免數據的主觀性。

因此，為降低評價過程中的模糊性并減少主觀因素的影響，本文提出基于球形模糊和TOPSIS的鞋靴外觀方案決策方法。首先，通過鞋靴構成分析鞋靴外觀，確定鞋靴外觀評價指標。其次，基于模糊模型集成決策專家的評價信息，同時引入猶豫度以獲得決策專家權重，解決評價指標權重和決策專家權重未知的決策問題。最后，結合TOPSIS貼近度的度量對備選方案進行決策排序，為鞋靴外觀方案的多屬性決策問題提供客觀有效的解決方法。

1 研究方法

1.1 球形模糊集

球形模糊集以隸屬度、非隸屬度和猶豫度多維度表達決策者的偏好信息，若X為給定的非空集合，則稱A={〈x，（μA（x），vA（x），πA（x））〉x∈X}為球形模糊集。其中μA（x）、vA（x）、πA（x）表示元素x對集合U的隸屬度、非隸屬度和猶豫度，即μA：X→［0，1］，vA：X→［0，1］，πA：X→［0，1］;且滿足條件0≤μ2A（x）+v2A（x）+π2A（x）≤1，x∈X。

設A=（μA，vA，πA）和B=（μB，vB，πB）為任意兩個不同的球形模糊集，λ為標量，且λ>0，則其基本運算定義為：

AB={（μ2A+μ2B-μ2Aμ2B）^1/2，vAvB，（（1-μ2B）π2A+（1-μ2A）π2B-π2Aπ2B）^1/2}（1）

AB={μAμB，（v2A+v2B-v2Av2B）^1/2，（（1-v2B）π2A+（1-v2A）π2B-π2Aπ2B）^1/2}（2）

λ·A={（1-（1-μ2A）λ）^1/2，vλA，（（1-μ2A）λ-（1-μ2A-π2A）λ）^1/2}（3）

Aλ={μλA，（1-（1-v2A）λ）^1/2，（（1-v2A）λ-（1-v2A-π2A）λ）^1/2}（4）

設A1，A2，…，An為Ai=（μAi，vAi，πAi）（i=1，2，…，n）為一組球形模糊數，w=（w1，w2，…，wn）T為權重向量，wi∈［0，1］，且∑ni=1wi=1，則球形模糊加權平均算子（SWAM）為：

SWAMw（A1，A2，…，An）=w1A1+w2A2+…wnAn=1-∏ni=1（1-μ2Ai）^wi1/2，∏ni=1v^wiAi，∏ni=1（1-μ2Ai）^wi-∏ni=1（1-μ2Ai-π2Ai）^wi1/2（5）

1.2 逼近理想解排序法

逼近理想解排序法（TOPSIS）的基本原理即最佳決策方案應該與正理想解（PIS）的距離最近，與負理想解（NIS）的距離最遠。設任意決策問題有m個備選方案和n個屬性，則定義決策矩陣為D=［fij］m×n，其中i=1，2，…，m;j=1，2，…，n;fij表示備選方案的屬性值。

TOPSIS的分析步驟如下：首先，決策矩陣D標準化處理后得到矩陣Dnormalized，即Dnormalized=［rij］m×n，其中rij=fij/∑mi=1f2ij^1/2。其次，加權標準化決策矩陣，即vij=wj·rij，其中wj為屬性的權重。再次，確定正理想解（v+i）和負理想解（v-i），即v+i=（max（vij）j∈I），（min（vij）j∈J）;v-i=（min（vij）j∈I），（max（vij）j∈J），其中I與收益標準相關，J與成本標準相關。繼而，通過歐氏距離計算備選方案與正負理想解之間的距離，即d+i=∑ni=1（vij-v+i）2^1/2，d-i=∑ni=1（vij-v-i）2^1/2。最后，依據距離計算備選方案Ai與理想解的貼近度Di，即Di=d-i/（d-i+d+i），通過Di的值對備選方案進行排序。

2 鞋靴外觀方案決策

2.1 多屬性決策流程

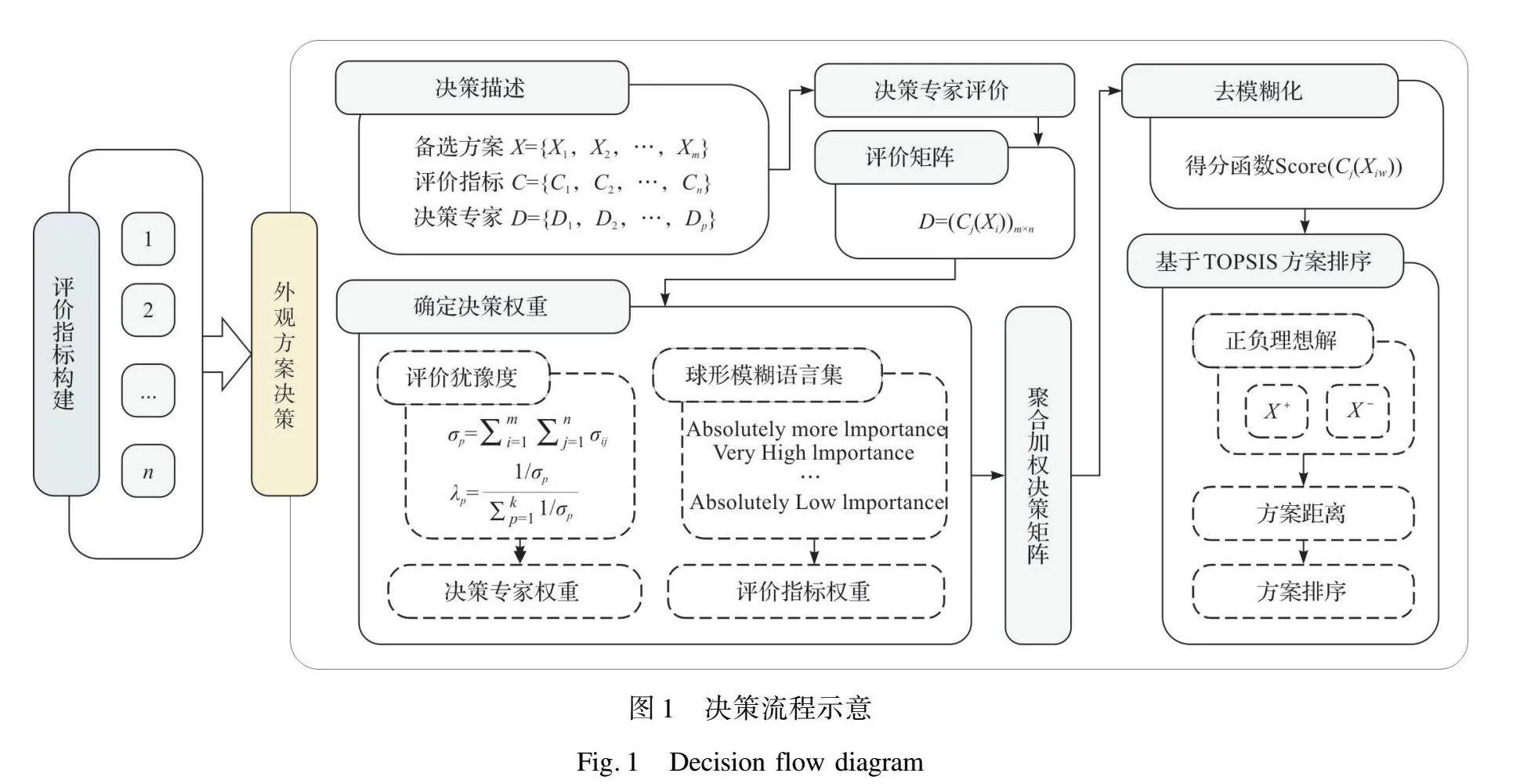
基于球形模糊集和TOPSIS的鞋靴外觀方案決策方法流程如圖1所示。該方法分為評價指標的構建和外觀方案的決策兩部分。評價指標的構建階段，通過對構成鞋靴外觀的組成部分的分析與研究，提取影響鞋靴外觀的關鍵評價指標。外觀方案的決策階段，基于球形模糊和TOPSIS對外觀方案進行評價和排序。利用模糊語言集將主觀性的語言評價量化為球形模糊數值;通過TOPSIS確定正負理想解，比較備選方案與正負理想解之間的距離，從而確定最優的備選方案，以指導鞋靴外觀設計的決策過程。

2.2 評價指標的構建

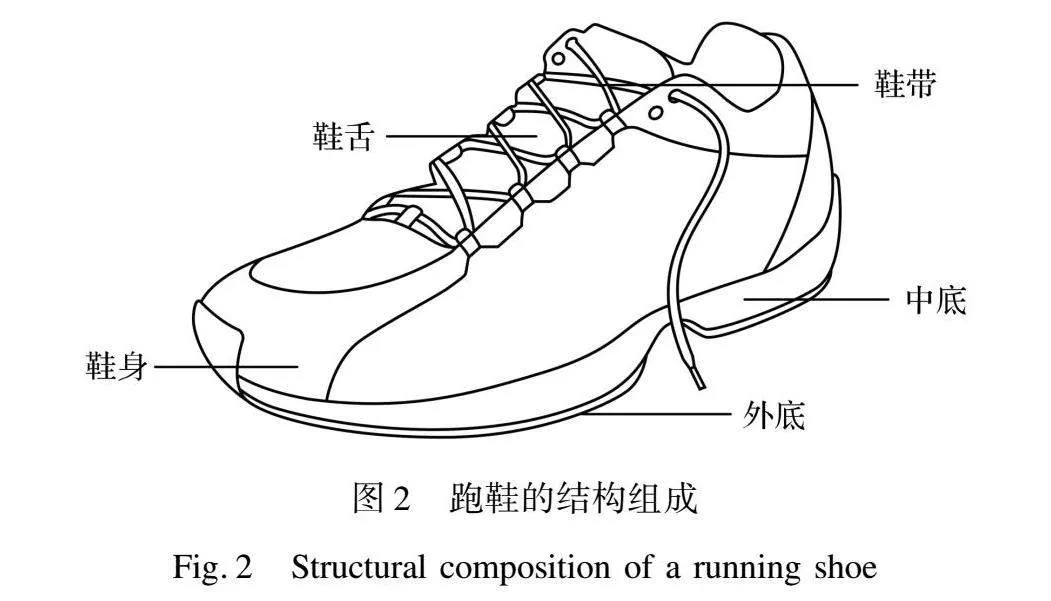
鞋靴可依據不同的特征和需求分為若干類別，本文以跑鞋為例探究鞋靴外觀方案的決策指標。構建跑鞋的外觀方案評價指標涉及多維度的考量因素，本文以外觀結構為切入點，將跑鞋外觀方案評價指標的構建按跑鞋結構分模塊展開，獲得跑鞋外觀的完整描述信息。國家標準《鞋類術語》中將旅游鞋的部件定義為前幫、后幫、鞋舌、鞋帶、鞋眼、內底、中底和外底，而旅游鞋與跑鞋在功能和設計方面存在相似之處;類似的工作還有Shieh等^［18］將跑鞋的外部結構解構為9類設計屬性，包括鞋底（中底外底）、鞋頭、孔眼、鞋舌、眉片、后跟、鞋面、鞋帶和鞋領。由于跑鞋設計風格的復雜性與多樣性，存在鞋頭、鞋幫、鞋面、孔眼與后跟具有統一設計語言的情況，也存在弱化眉片與鞋領設計的情況。為避免破壞跑鞋外觀的整體性，本文將鞋底以上除鞋舌和鞋帶外的部分作為整體進行評價。此外，鞋墊由于其位置的隱蔽性與跑鞋外觀的聯系并不顯著，暫不予以分析。綜合考慮，本文根據跑鞋的外觀結構特征，將跑鞋分解為五個構造組成部分，包括鞋帶、鞋舌、鞋身、中底和外底，具體結構如圖2所示。評價指標的設問僅針對跑鞋的外觀方案，涵蓋設計風格的協調性、色彩搭配的巧妙性、跑鞋裝飾的藝術性及材質工藝的精細性等視覺審美層面的感知，但不涉及品牌、價格和功能的評價，以確保評價的客觀性和視覺導向。

2.3 方案多屬性決策

2.3.1 方案決策描述

鞋靴外觀方案的多屬性決策問題中，假設存在m個鞋靴備選方案，集合X={X1，X2，…，Xm}（m≥2）表示待決策的方案，在對方案進行選擇時參考n個評價指標，集合C={C1，C2，…，Cn}表示有限的評價指標，w={w1，w2，…，wn}表示評價指標的權重，且滿足（∑nj=1wj=1，wj∈［0，1］）。為保障決策的合理性和科學性，邀請專業人員組成決策專家組，D={D1，D2，…，Dp}表示決策專家，λ={λ1，λ2，…，λi}表示決策專家的權重，且滿足（∑pi=1λi=1，λi∈［0，1］）。

2.3.2 方案決策步驟

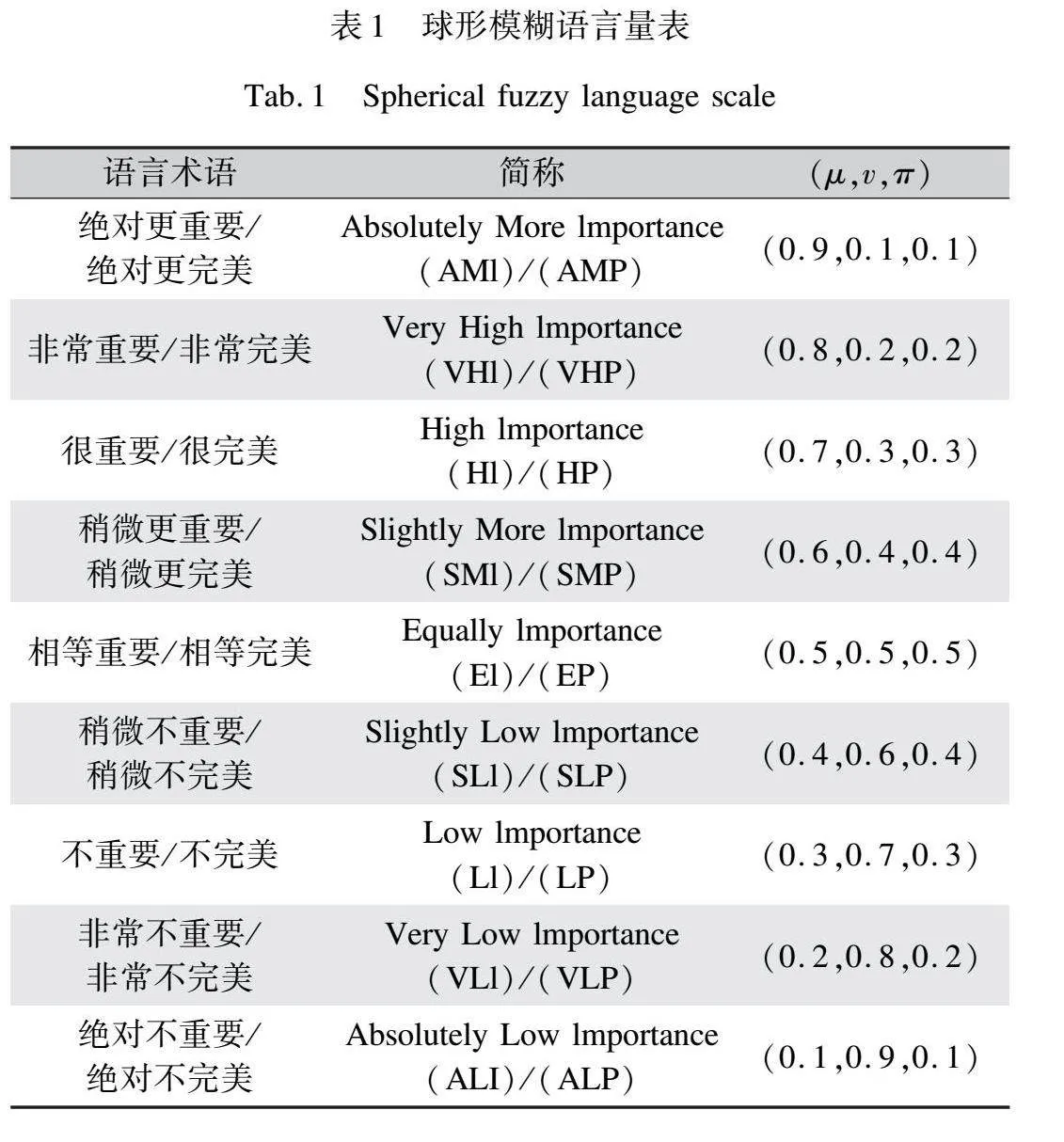
步驟1：決策專家語言評價。決策專家以語言評價的形式對備選方案對應評價指標進行決策賦值，語言術語與球形模糊數值的對應關系如表1所示。

步驟2：構建球形模糊決策矩陣。基于決策專家的評價結果構建球形模糊決策矩陣，Cj（Xi）表示備選方案Xi（i=1，2，…，m）在評價指標Cj（j=1，2，…，n）中的評價結果，D=（Cj（Xi））m×n表示球形模糊決策矩陣，矩陣構造如式（6）所示。

D=（Cj（Xi））m×n=（μ11，v11，π11）（μ12，v12，π12）…（μ1n，v1n，π1n）（μ21，v21，π21）（μ22，v22，π22）…（μ2n，v2n，π2n）（μm1，vm1，πm1）（μm2，vm2，πm2）…（μmn，vmn，πmn）（6）

步驟3：確定決策專家權重。決策過程中決策專家的猶豫模糊程度反映決策結果的不確定程度，參考林原等^［19］的研究，將專家猶豫度分為“很小”“小”“一般”3個等級，用于表示決策專家決策結果遲疑度的遞增。決策專家Dp決策過程的猶豫度σp如式（7）所示。猶豫度越大，決策專家的不確定程度越大，評價結果的可信任度越小。決策專家的客觀權重λp如式（8）所示。

σp=∑mi=1∑nj=1σij（7）

λp=1/σp∑kp=11/σp（8）

步驟4：構建聚合加權決策矩陣。根據步驟3得出的決策專家權重，運用式（5）中給出的球形模糊加權平均算子（SWAM）聚合決策專家的評價結果，得到所有決策專家對備選方案評價指標的聚合決策矩陣。

步驟5：確定評價指標權重。決策專家結合自身專業知識和經驗偏好，確定評價指標的重要程度，同樣根據球形模糊語言量表得到評價指標的決策矩陣，得到評價指標的權重。

步驟6：構建聚合加權決策矩陣。綜合評價指標的權重和備選方案的評價結果，通過式（5）構建聚合加權球形模糊決策矩陣，決策矩陣如式（9）所示。

D=（Cj（Xiw））m×n=（μ11w，v11w，π11w）（μ12w，v12w，π12w）…（μ1nw，v1nw，π1nw）（μ21w，v21w，π21w）（μ22w，v22w，π22w）…（μ2nw，v2nw，π2nw）（μm1w，vm1w，πm1w）（μm2w，vm2w，πm2w）…（μmnw，vmnw，πmnw）（9）

步驟7：決策矩陣去模糊化。通過得分函數對聚合加權決策矩陣進行去模糊化，得分函數如式（10）所示。

Score（Cj（Xiw））=（μijw-πijw）2-（vijw-πijw）2（10）

步驟8：確定正負理想解。根據步驟7中計算出的得分值，確定球形模糊正理想解（SF-PIS）和球形模糊負理想解（SF-NIS）。SF-PIS和SF-NIS如式（11）（12）所示。

X+={Cj，max〈Score（Cj（Xiw））〉j=1，2，…，n}（11）

X-={Cj，min〈Score（Cj（Xiw））〉j=1，2，…，n}（12）

步驟9：計算備選方案距離。通過歸一化歐幾里德距離確定備選方案Xi與SF-PIS及SF-NIS之間的距離，與SF-NIS和SF-PIS的距離如式（13）（14）所示。

D（Xi，X-）=12n∑ni=1（（μxi-μx-）2+（vxi-vx-）2+（πxi-πx-）2）（13）

D（Xi，X+）=12n∑ni=1（（μxi-μx+）2+（vxi-vx+）2+（πxi-πx+）2）（14）

步驟10：排序備選方案。利用式（15）計算修正后的貼近度^［20］，確定最優備選方案并基于貼近度的值對備選方案進行排序。

ξ（Xi）=D（Xi，X+）Dmin（Xi，X+）-D（Xi，X-）Dmax（Xi，X-）（15）

3 應用案例

3.1 案例決策過程

以鞋靴外觀為研究的主題，本文選取5雙不同品牌的男式跑鞋以確保所選方案具有代表性和全面性，同時保證不同品牌跑鞋間造型、色彩及材質的差異性和多樣性。確定跑鞋方案后篩選清晰并且符合要求的左視、右視、后視、底視、四分之三側視5種角度的跑鞋外觀圖像作為實驗圖像，對5雙跑鞋（X1、X2、X3、X4和X5）進行方案決策，不同角度的跑鞋外觀圖像如圖3所示，其中方案評價指標為鞋帶、鞋舌、鞋身、中底和外底（C1、C2、C3、C4和C5）。在評估過程中，6位決策專家（DM1、DM2、DM3、DM4、DM5和DM6）包括從事鞋服行業的工作者、執教鞋服設計的教授和攻讀鞋服專業的研究生。

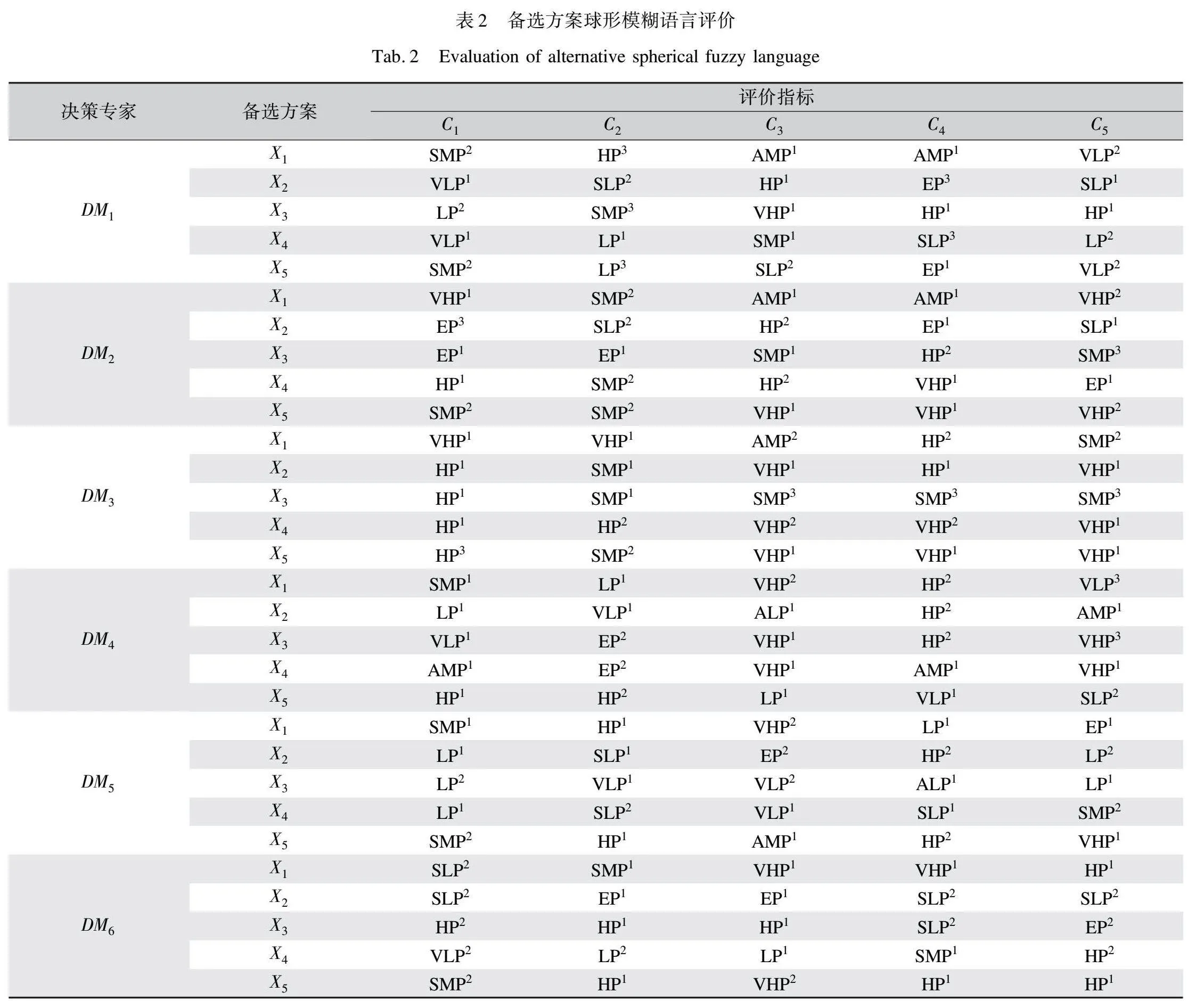
決策專家的語義評價以表1中跑鞋方案的語言術語的形式收集，語義評價的對象為備選方案的外觀，不涉及品牌、價格及功能等其他因素。同時，決策專家根據提供的跑鞋實驗圖像和主觀感知評價確定決策過程中的猶豫等級，備選方案的原始評價結果如表2所示。

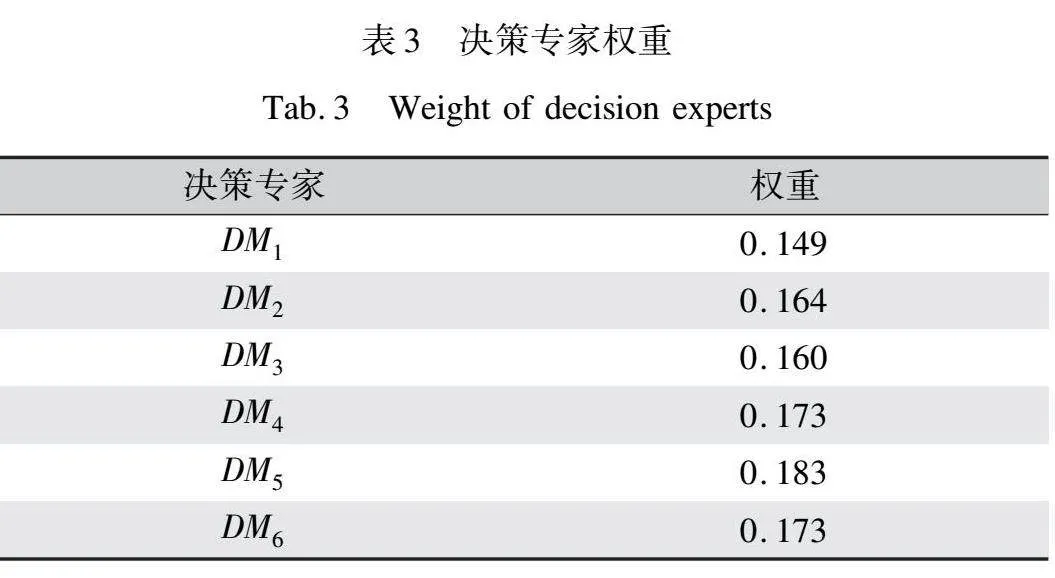
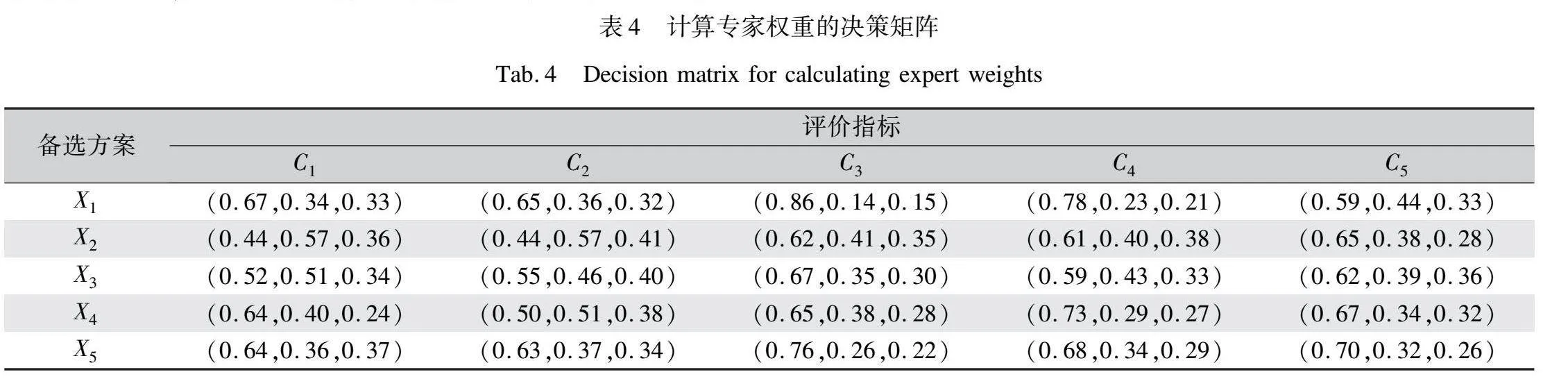
基于決策專家的決策過程中猶豫模糊程度確定決策專家的權重，通過式（7）（8）與表2計算得到決策專家的權重，如表3所示。專家DM5的猶豫度最低，其決策權重為0.183;而專家DM1的猶豫度最高，其決策權重為0.149。雖然決策專家的決策權重存在一定的波動，但整體波動范圍較小，表明決策專家在對備選方案進行評價時具備專業性和穩定性，其決策差異不會對決策結果產生較大影響。結合決策專家的評價結果與決策專家的權重，由SWAM運算得到的決策矩陣如表4所示。

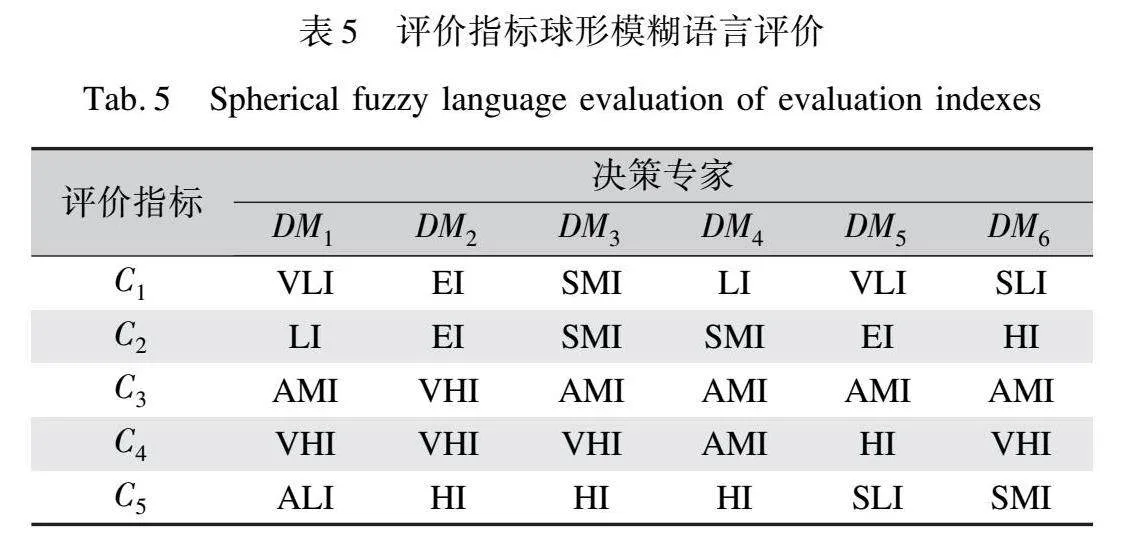
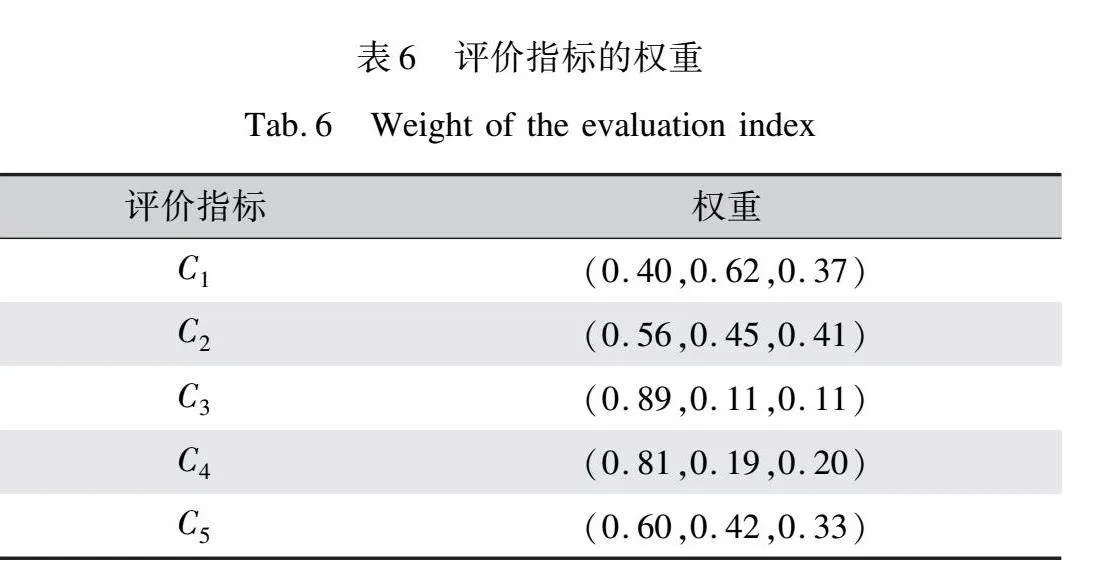
同樣以表1中的語言術語的形式得到決策專家對評價指標的判斷矩陣，語言評價結果如表5所示。通過式（5）確定評價指標的權重，評價指標的權重如表6所示。由表5與表6的評價結果與權重可知，鞋身（C3）和中底（C4）在跑鞋外觀方案決策中重要程度相對較高，分別為（0.89，0.11，0.11）和（0.81，0.19，0.20），其次是外底（C5）和鞋舌（C2），而鞋帶（C1）的重要程度相對最低，僅為（0.40，0.62，0.37）。鞋身和中底是跑鞋外觀的主要組成部分之一，承擔塑造外觀形態的關鍵作用。鞋身的設計涵蓋形狀、線條和色彩等要素，其材質的選擇及色彩的搭配將直接影響跑鞋的視覺效果和美觀程度。作為固定鞋身的部件，鞋帶的主要功能是調節跑鞋的松

緊程度以保證腳踝安全，鞋帶的設計變化受跑鞋其他組成部分的影響。由于其功能定位和設計特點，在評估評價指標的重要性時，鞋帶的影響被認為相對較小，對跑鞋外觀設計的整體貢獻較為有限，相對而言，其他評價指標更為顯著。

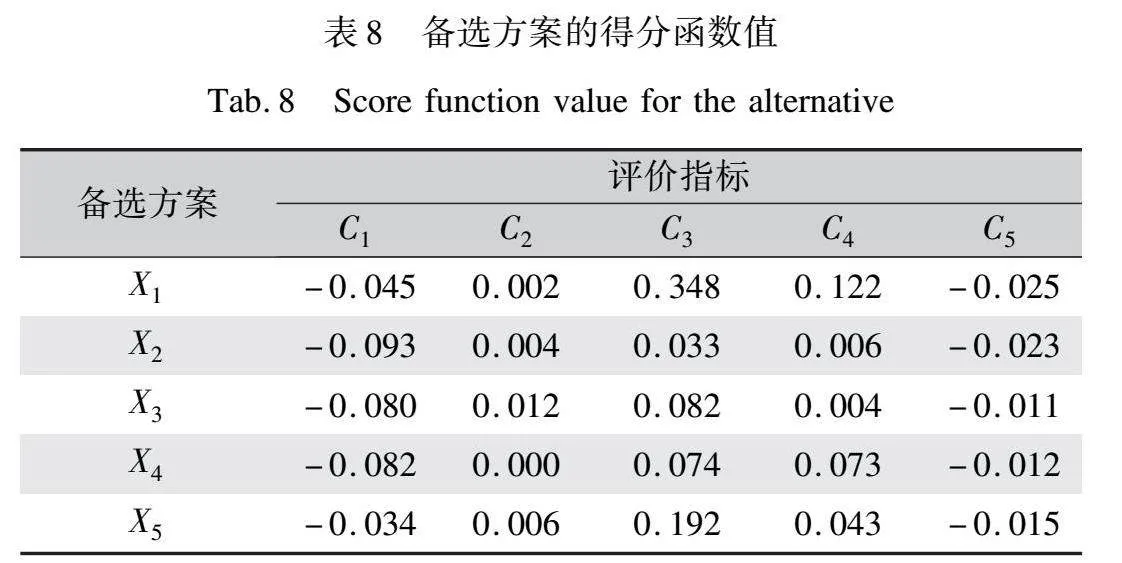
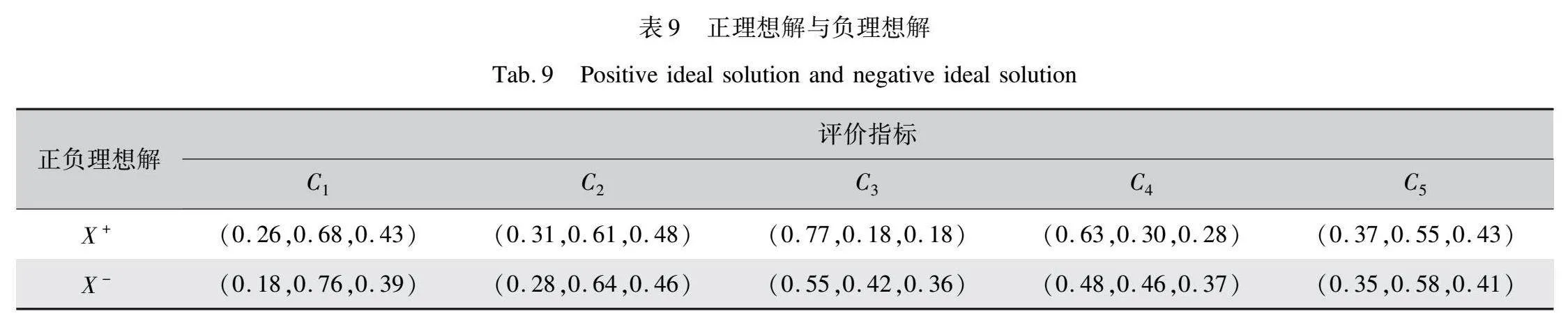
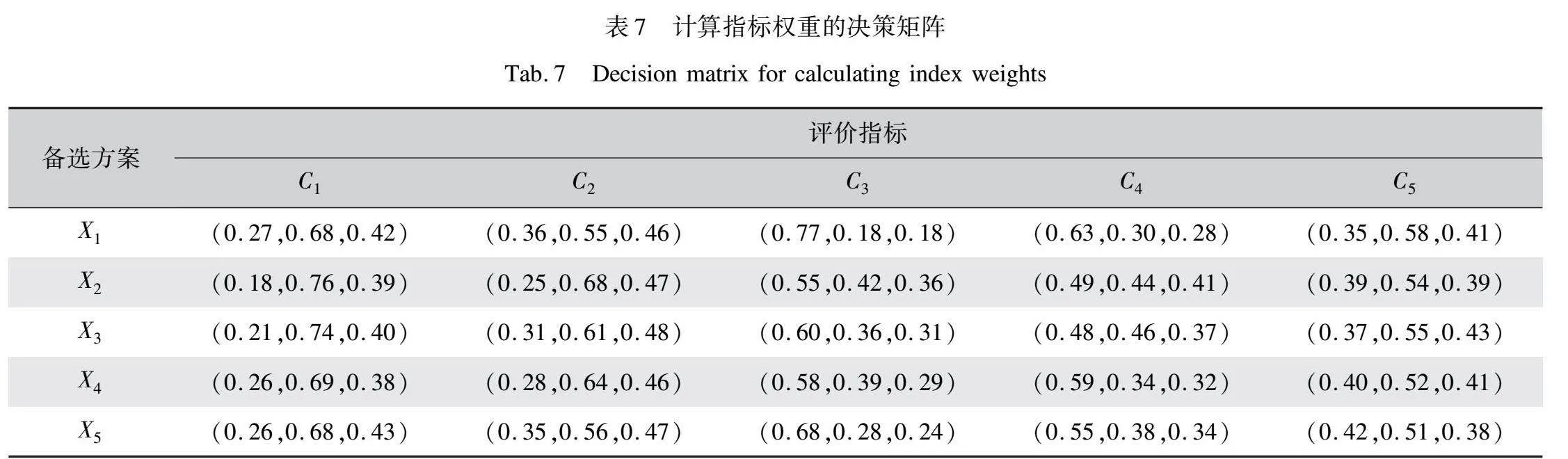
在確定評價指標的權重后，基于式（2）與表4中給出的決策矩陣構建聚合加權球形模糊決策矩陣，如表7所示。通過式（10）得分函數對聚合加權決策矩陣進行去模糊化，備選方案的得分函數值如表8所示，其中，每列中得分最高的為PIS，得分最低的為NIS。根據最高和最低得分得到相應的球形模糊正理想解（SF-PIS）和球形模糊負理想解（SF-NIS），正負理想解如表9所示。

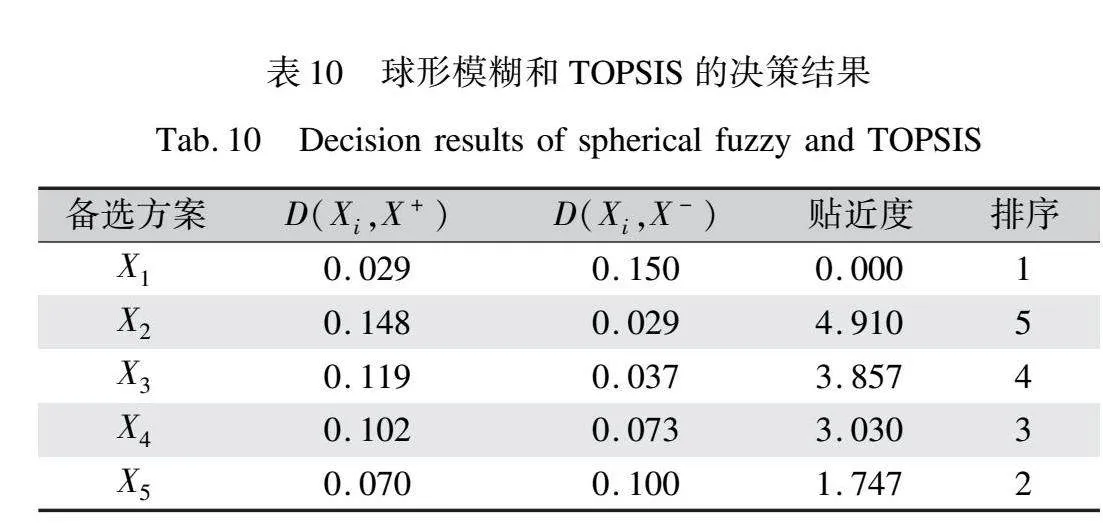
通過式（13）（14）計算備選方案Xi的專家評價值與SF-PIS及SF-NIS之間的距離，確定5個備選方案到SF-NIS的最大距離和到SF-PIS的最小距離。基于式（15）計算貼近度，并根據貼近度進行方案排序，則決策結果如表10所示。決策結果表明最優備選方案為X1，其設計風格與決策專家的審美偏好契合度較高，明顯優于其他四種方案;X2為最劣備選方案，其與正理想解的距離最遠，離負理想解的距離最近。此外，總體備選方案的排序為X1>X5>X4>X3>X2。

3.2 決策方法比較

由于球形模糊TOPSIS通過球形模糊集量化不確定性評價信息，基于TOPSIS反映備選方案之間的差距。為驗證鞋靴外觀方案決策方法的有效性與優越性，參考Zou等^［21］提出的熵權TOPSIS決策法和馮卉等^［22］提出的直覺模糊VIKOR決策法，與本文所提出的決策方法進行對比。為直觀地分析兩種方法的可行性，將直覺模糊VIKOR決策法調整為球形模糊VIKOR決策法，將熵權TOPSIS決策法調整為直覺模糊TOPSIS決策法。

3.2.1 直覺模糊TOPSIS決策法

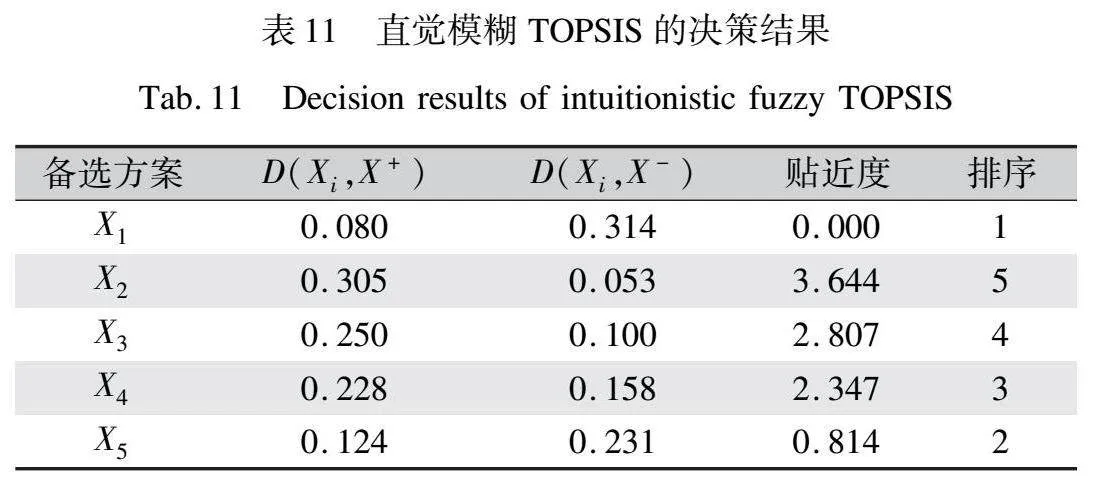
基于表2和表5決策專家給出的評價結果，對照直覺模糊語言量表得到直覺模糊值，確定決策專家的權重和評價指標的權重后使用直覺模糊加權平均算子進行匯總，得到加權后直覺模糊決策矩陣，計算其直覺模糊正理想解和直覺模糊負理想解。通過備選方案和正理想解負理想解之間的距離，得到貼近度和決策排序如表11所示。直覺模糊TOPSIS決策法的貼近度表明，最優決策方案為X1，備選方案排序的優劣排序為X1>X5>X4>X3>X2，與球形模糊TOPSIS決策法的決策結果保持一致。

3.2.2 球形模糊VIKOR決策法

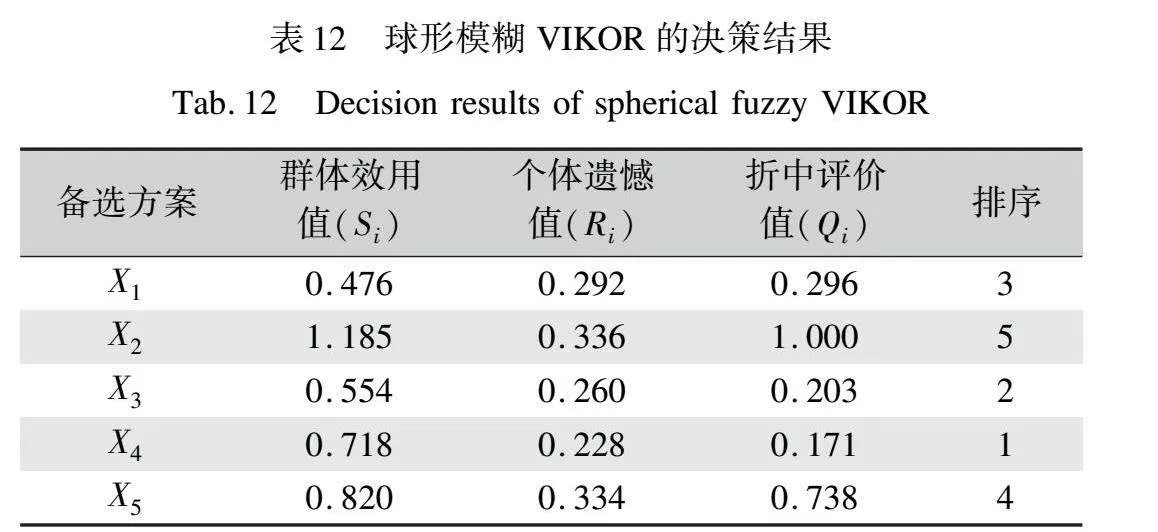
基于評價指標最優值確定的球形模糊正負理想解如表9所示。多準則妥協解排序（VIKOR）通過考慮綜合群體效用與個體遺憾對評價結果進行排序，兼顧決策者效用偏好的同時，綜合評價指標實現群體效益最大化與個體遺憾最小化的折中。群體效用值（Si）、個體后悔值（Ri）和折中評價值的計算結果如表12所示，其中決策系數取0.5，最優決策方案為X4，備選方案排序的優劣排序為X4>X3>X1>X5>X2。備選方案X4、X3和X1的排序結果與球形模糊TOPSIS決策法的決策結果存在差異。但決策方案X4不滿足可接受優勢準則，群體效用值非最小值，將Qi值的排序代入可接受優勢準則計算后，排序為第三的決策方案X1滿足條件，則備選方案X1、X3和X4均為理想折中方案。

由直覺模糊TOPSIS決策法和球形模糊VIKOR決策法的決策結果可知，與球形模糊TOPSIS的排序結果大致相同，充分證明方法的合理性和可行性。相較于直覺模糊，球形模糊集賦予決策專家更多的信息表達空間，深入挖掘事物本身的模糊性，得出不同備選方案間的評價結果差異性更大，貼近度較為分散;而TOPSIS能有效避免數據的主觀性，充分利用原始數據的信息，刻畫多個影響指標的綜合影響力度，VIKOR排序后的最佳備選方案可能不唯一，但TOPSIS通過歐幾里德距離得到客觀的備選方案排序及最優解。

4 結 語

針對以語言文本為評價信息、決策權重未知的鞋靴外觀方案選擇問題，本文構建基于球形模糊數和TOPSIS決策框架，實現對鞋靴外觀方案的全面系統性評估。定義跑鞋外觀決策方案的多屬性評價指標為鞋帶、鞋舌、鞋身、中底和外底五個維度。以球形模糊數衡量評價數據，避免語言文本的主觀性與模糊性。通過決策專家的評價猶豫度確定專家權重，基于決策專家對備選方案評價指標的評價值和決策權重，采用TOPSIS方法確定備選方案與理想解距離最短、與負理想解距離最遠的解，從而得到最具優勢的備選方案。

基于球形模糊和TOPSIS的決策方法將鞋靴外觀設計中感性模糊的決策方式量化，有效克服決策過程中的主觀盲目性，增強鞋靴產品的市場競爭力和消費者接受度，為設計決策提供一定的參考價值。但研究也存在局限性，其主要聚焦于方法的構建與理論的探討層面，對于方法在實際設計過程的應用實施及效果驗證尚顯不足。未來的研究應當將方法理論與實際應用緊密結合，深化理論框架，以增強其在解決設計問題時的可靠性和多種設計背景下的普適性。

參考文獻：

［1］PROMJUN S， SAHACHAISAEREE N. Factors determining athletic footwear design： A case of product appearance and functionality［J］. Procedia-Social and Behavioral Sciences， 2012， 36： 520-528.

［2］李華. 造型藝術在皮革鞋靴設計中的應用研究［J］. 中國皮革， 2024， 53（3）： 63-67.

LI H. Application of plastic arts in leather footwear design［J］. China Leather， 2024， 53（3）： 63-67.

［3］齊耐斌. 時尚運動休閑鞋的創新設計與實踐［J］. 北京皮革， 2023， 48（12）： 60-63.

QI N B. Innovative design and practice of fashion sports and leisure shoes［J］. Beijing Leather， 2023， 48（12）： 60-63.

［4］趙堅， 趙強， 周海燕. 鞋靴仿生設計思維與方法的研究［J］. 中國皮革， 2013， 42（16）： 122-124.

ZHAO J， ZHAO Q， ZHOU H Y. Research on the idea and method of footwear bio-mimetic design［J］. China Leather， 2013， 42（16）： 122-124.

［5］SPURRIER S， ALLEN T， GRANT R A. Investigating foot morphology in rock climbing mammals： Inspiration for biomimetic climbing shoes［J］. Biomimetics， 2023， 8（1）： 8.

［6］XU D D， WU C F， WANG C S. A study on perception of visual-tactile and color-texture features of footwear leather for symmetric shoes［J］. Symmetry， 2023， 15（7）： 1462.

［7］RYU S， STEFANYSHYN D， KONG S， et al. Effects of a curved heel shape in a running shoe on biomechanical variables and comfort［J］. Applied Sciences， 2021， 11（8）： 3613.

［8］BISHOP C， BUCKLEY J D， ESTERMAN A E， et al. The running shoe comfort assessment tool （RUN-CAT）： Development and evaluation of a new multi-item assessment tool for evaluating the comfort of running footwear［J］. Journal of Sports Sciences， 2020， 38（18）： 2100-2107.

［9］裴卉寧， 譚昭蕓， 劉鑫宇， 等. 基于單值中智集和云聚類的產品造型設計決策方法［J］. 浙江大學學報（工學版）， 2022， 56（12）： 2367-2378.

PEI H N， TAN Z Y， LIU X Y， et al. Decision method for product styling design based on single-valued neutrosophic sets and cloud clustering［J］. Journal of Zhejiang University （Engineering Science）， 2022， 56（12）： 2367-2378.

［10］楊延璞， 蘭晨昕， 雷紫荊， 等. 產品造型設計多階段網絡耦合決策方法研究［J］. 圖學學報， 2021， 42（6）： 1018-1026.

YANG Y P， LAN C X， LEI Z J， et al. Research on multi-stage network coupling decision-making method of product styling design［J］. Journal of Graphics， 2021， 42（6）： 1018-1026.

［11］SHIEH M D， LI Y F， YANG C C. Product form design model based on multiobjective optimization and multicriteria decision-making［J］. Mathematical Problems in Engineering， 2017（1）： 1-15.

［12］MAO L X， LIU R， MOU X， et al. New approach for quality function deployment using linguistic Z-numbers and EDAS method［J］. Informatica， 2021， 32（3）： 565-582.

［13］ZADEH L A. Fuzzy sets［J］. Information and Control， 1965， 8（3）： 338-353.

［14］ATANASSOV K T. Intuitionistic fuzzy sets［J］. Fuzzy Sets and Systems， 1986， 20（1）： 87-96.

［15］TORRA V. Hesitant fuzzy sets［J］. International Journal of Intelligent Systems， 2010， 25（6）： 529-539.

［16］YAGER R R. Pythagorean membership grades in multicriteria decision making［J］. IEEE Transactions on Fuzzy Systems， 2014， 22（4）： 958-965.

［17］MAHMOOD T， ULLAH K， KHAN Q， et al. An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets［J］. Neural Computing and Applications， 2019， 31： 7041-7053.

［18］SHIEH M D， YEH Y E. Developing a design support system for the exterior form of running shoes using partial least squares and neural networks［J］. Computers and Industrial Engineering， 2013， 65（4）： 704-718.

［19］林原， 戰仁軍， 吳虎勝. 基于混合改進TOPSIS的裝備供應商選擇方法［J］. 工業工程與管理， 2021， 26（2）： 75-82.

LIN Y， ZHAN R J， WU H S. Research on equipment supplier selection method based on mixed information and improved TOPSIS［J］. Industrial Engineering and Management， 2021， 26（2）： 75-82.

［20］GNDODU F K， KAHRAMAN C. Spherical fuzzy sets and spherical fuzzy TOPSIS method［J］. Journal of Intelligent and Fuzzy Systems， 2019， 36（1）： 337-352.

［21］ZOU T， GUO P B， WU Q L. Applying an entropy-weighted TOPSIS method to evaluate energy green consumption revolution progressing of China［J］. Environmental Science and Pollution Research， 2023， 30： 42267-42281.

［22］馮卉， 宋寶軍， 邢清華. 基于直覺模糊VIKOR決策的反導作戰預案評估方法［J］. 火力與指揮控制， 2022， 47（6）： 17-21.

FENG H， SONG B J， XING Q H. Anti-missile operational scheme evaluation method based on intuitionistic fuzzy VIKORMADM［J］. Fire Control & Command Control， 2022， 47（6）： 17-21.

A decision method of shoe appearance schemes based on spherical fuzzy and TOPSIS

ZHANG Chi， WANG Xiangrong

LUO Xiangdong， WU Meng， QIANG Wei， ZHANG Zhetao

（College of Design & Art， Shaanxi University of Science & Technology， Xi’an 710021， China）

Abstract： In the contemporary consumer market， shoes， as a functional and aesthetic value of goods， have transcended the simple category of necessities of life. They have become important vehicles for individuals to express their personal style and fashion attitudes. The consumer psychology of shoes has also changed from the basic needs to the pursuit of quality upgrade. Consumers pay increasing attention to the personalized design and cultural connotation of products， as well as their personal lifestyle fit. As a result， the creativity and differentiation of shoe design has become the core element of brand competition. Most of the existing research on shoe design innovation focuses on the appearance design and aesthetic analysis， while little attention is paid to the evaluation of shoe appearance schemes. But the appearance design of shoes is also of great significance， and it not only relates to the visual presentation of design aesthetics， but also directly affects the product’s market competitiveness and consumer acceptance. However， the evaluation of design schemes often faces the double challenges of fuzziness and subjectivity. The issue of how to select the optimal design solution remains a pressing practical problem.

In order to realize the scientific decision and evaluation of shoe appearance schemes， fuzzy and complex problems， and obtain objective and reasonable weight distribution， a method of multi-attribute decision-making method based on spherical fuzzy TOPSIS is proposed. First of all， according to the structure of shoes， the evaluation indexes are determined， including laces， tongue， body， midsole and outsole. The evaluation index focuses on the appearance of running shoes， and the shoes are evaluated from the visual aesthetic point of view of design style， color collocation， decorative arts and material technology， excluding the influence of brand， price， and function， to ensure visual orientation. Secondly， the evaluation language of decision-making experts is transformed into quantitative information by reference to the linguistic scale of spherical fuzzy sets to describe the decision-making situation and obtain the weight of the evaluation index. At the same time， in order to avoid the influence of the difference of decision-making experts on the evaluation results， the evaluation hesitation degree of decision-making experts is introduced to determine the weight of decision-making experts. Finally， based on the TOPSIS method， the relative importance of the evaluation indexes is characterized， and the closeness between the alternatives and the positive and negative ideal solutions is analyzed， so as to achieve the optimal ranking of shoe appearance schemes.

This study takes men’s run8nry2jcVk8rHNZlrjR6i/gGTEImnHF7J2WTv7cwhtkQ=ning shoes as the decision object to verify the feasibility of the method. The evaluation results indicate that the body and midsole are relatively more important in the decision-making process for the appearance of running shoes. The outsole and tongue are less important， while the laces are considered the least important. The scheme method based on spherical fuzzy TOPSIS can comprehensively consider the psychological factors of decision-making experts， judge the appearance difference of different shoe-shoe appearance schemes and make effective decisions. In addition， compared with the other two methods， the spherical fuzzy set gives more information expression space to decision-makers， and further excavates the fuzziness of things themselves， which is helpful to analyze the differences of evaluation results among different options. TOPSIS can effectively avoid the subjectivity of data and make full use of the information of original data.

The decision-making method based on spherical fuzzy TOPSIS is driven by the preference of decision-making experts. It scientifically quantifies the perceptual fuzzy decision-making mode in shoe design， effectively overcomes the subjective blindness in the decision-making process， and enhances the market competitiveness and consumer acceptance of footwear products， providing certain reference value for design decision-making. However， there are some limitations in the research by mainly focusing on the construction of the method and the theoretical discussion， and the application of the method in the actual design process and the effect verification are still insufficient. To this end， future research should focus on the deep integration of theory and practice， with a view to achieving practical utility maximization problem of decision-making methods.

Key words： spherical fuzzy set; TOPSIS; weight; shoe; appearance; scheme decision