例析高階思維結構圖在高中數學解題中的應用

【摘要】高中學生在數學解題中經常會遇到復雜題型，題干信息內容較多、題目碎片化，學生難以直接找到關鍵點，為了有效地解決這一問題，就需要教師引導學生轉變學習方法，采用逆向、發散、組合等多種形式，實現對題干信息的整理、選擇合適的高階思維結構圖構建新的思維過程，在這期間，需要遵循整體性、啟發性、生成性原則，通過分析、評價和創造，完成題目的整合與可視化，以深入理解題干信息，降低解題難度，促進學生高階思維發展.

【關鍵詞】思維結構圖；高中數學；解題

1前言

高階思維結構圖作為一種思維工具，基于分析、評價、創造等高層次思維，輔助學生形成數學解題技巧、認知思路，這種結構圖的方式可以通過圖文結合的形式直觀地呈現出思考路徑，有助于完善學生的認知情況，加深個人記憶理解.以高中數學解題為例，需要在應用中遵循“整體性—啟發性—生成性”原則，鼓勵學生結合問題，分析知識點內容，將零散的信息分類、整合，以快速把握主要內容，在縱橫對比中，多角度分析題目條件、結論關系，選擇最優解題路徑.啟發性原則要求教師遵循由淺入深、循序漸進的方式引導學生自主思考，通過“問題導向、探究交流”輔助學生實現知識點的轉化，逐層剖析數學模型，逐步加深個人對數學知識的認知，提升學生的思考能力.通過構建結構圖，讓學生把握問題本質、探尋解題規律，因而形成了“學習方法—嘗試解題—理解問題—舉一反三”的思考路徑，助推創新，讓學生在學習數學知識的基礎上，發散思維、拓寬視野，實現知識的遷移與應用.

2高階思維結構圖的應用方法

高階思維結構圖的繪制可以歸納為五個步驟，即理—選—繪—驗—修.在這5個步驟中，不同環節體現的高階思維內容有所差異，以“理”“繪”為例，主要培養學生的分析能力、信息收集能力以及結構的繪制能力，“驗”則表示的是評價能力，確保繪制結構的邏輯性與準確性，在這5個步驟中充分地展現出了數學解題本質即“逐步接近結果目標”，這期間可以逆推、正推，只要找到已知條件與所求問題之間的聯系，就可以梳理出清晰的思維結構圖，并由此找到解決復雜問題的方法.

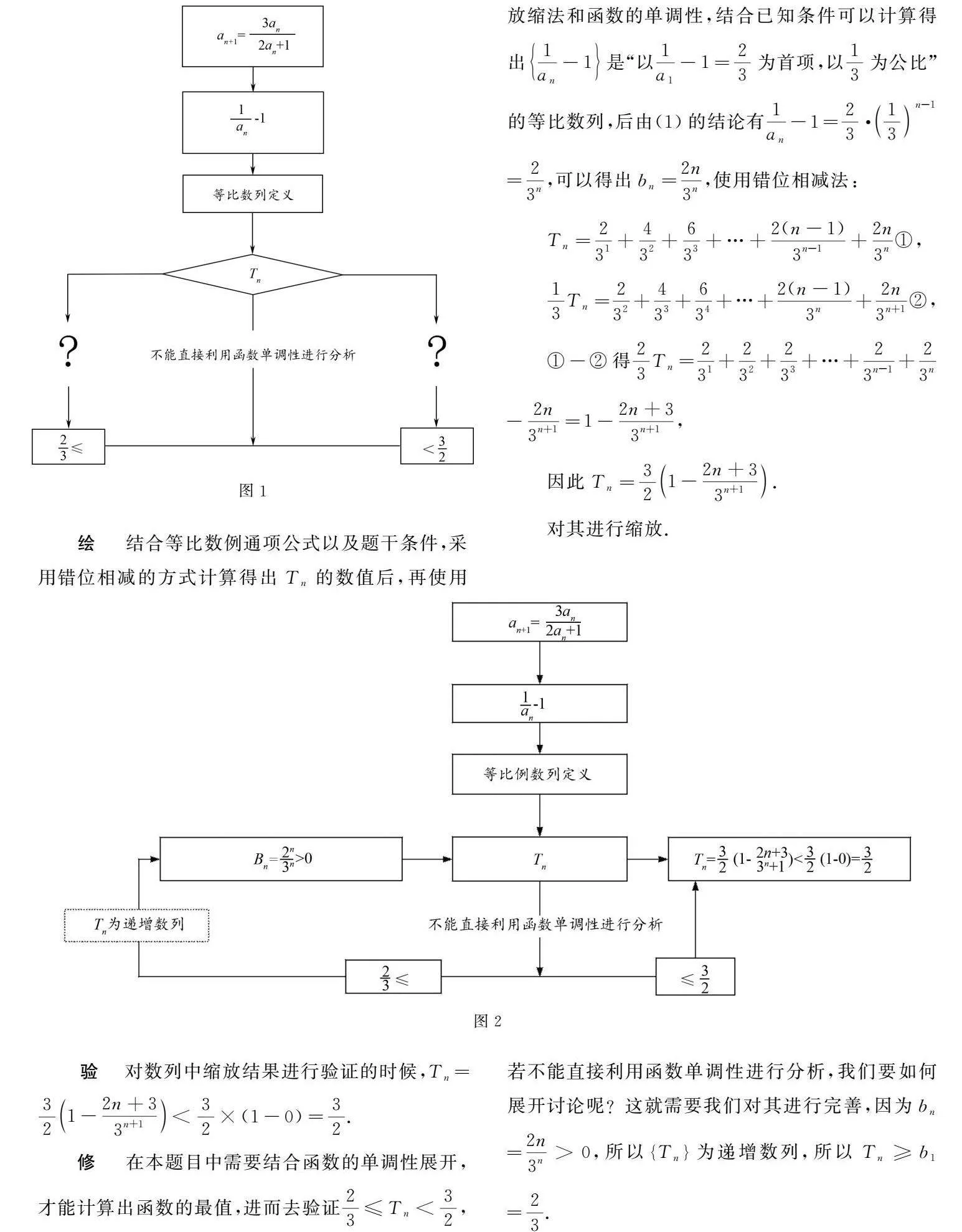
例題已知數列an的首項為a1=35，且滿足an+1=3an2an+1.

（1）求證：數列1an－1為等比數列；

（2）設bn=n1an－1，記數列bn的前n項和為Tn，求Tn，并證明：23≤Tn<32.

理本題目是在考查學生對比例知識以及反證法與放縮法的應用能力，需要先找到通項公式，發現無法直接利用通項公式進行函數單調性的求解，需要對其進行適當放縮，并根據函數單調性求解出函數最值.對第（1）問，若想要證明其是等比數列，通常情況下數列中的任意兩個相鄰項的比值相等（等比數列的概念），再結合第（1）問的結論，利用等比數列通項公式以及題干信息解第（2）問.

選為此可以采用雙向推理的方式將題干中的信息（已知條件）和結論進行系統的呈現，輔助學生梳理解題細節，初步整理情況如下（見圖1）.

繪結合等比數例通項公式以及題干條件，采用錯位相減的方式計算得出Tn的數值后，再使用放縮法和函數的單調性，結合已知條件可以計算得出1an－1是“以1a1－1=23為首項，以13為公比”的等比數列，后由（1）的結論有1an－1=23·13n－1=23n，可以得出bn=2n3n，使用錯位相減法：

Tn=231+432+633+…+2（n－1）3n－1+2n3n①，

13Tn=232+433+634+…+2（n－1）3n+2n3n+1②，

①-②得23Tn=231+232+233+…+23n－1+23n－2n3n+1=1－2n+33n+1，

因此Tn=321－2n+33n+1.

對其進行縮放.

驗對數列中縮放結果進行驗證的時候，Tn=321－2n+33n+1＜32×（1－0）=32.

修在本題目中需要結合函數的單調性展開，才能計算出函數的最值，進而去驗證23≤Tn＜32，若不能直接利用函數單調性進行分析，我們要如何展開討論呢？這就需要我們對其進行完善，因為bn=2n3n＞0，所以Tn為遞增數列，所以Tn≥b1=23.