立體幾何單元復習課

【摘要】本文通過一節(jié)案例課的思路分析，將立體幾何中的最短距離問題通過劃歸的方式與平面解析幾何聯(lián)系到一起.學生通過感受動態(tài)幾何中展開平面、證明全等、還原長度關(guān)系、求解線段長度的流程感受到數(shù)學中不同模塊的聯(lián)系，深化數(shù)形結(jié)合的數(shù)學思想.

【關(guān)鍵詞】立體幾何；最短距離；解題技巧

1教學內(nèi)容分析

立體幾何是高中數(shù)學的重要章節(jié)之一，到此階段高三學生已經(jīng)完成了一輪復習，對高中整體內(nèi)容有了一定的認知.在此節(jié)點，借助“最短距離”問題使學生回顧和建構(gòu)完整的立體幾何知識體系，以具體的棱柱、棱錐、旋轉(zhuǎn)體構(gòu)建點、線、面間位置框架，進行熟練的轉(zhuǎn)化和遷移.

立體幾何中的“距離”問題是定量分析空間幾何元素（點、線、面）間位置關(guān)系的重要幾何量.在研究距離問題時，常將空間問題轉(zhuǎn)化為平面問題處理，這是化歸思想在立體幾何中的具體應用.在求解空間距離的相關(guān)問題時，一般包括三個部分：求作、論證和計算，這三部分是不可分割的整體.通過這一章節(jié)內(nèi)容的學習，學生回顧之前與旋轉(zhuǎn)體有關(guān)的表面積問題的求解思路，同時也掌握在展開過程中分類討論的精確性和還原截面的方法.

2學情分析

高三學生在之前的立體幾何學習中已經(jīng)學習了點到面、線到面、線到線、面到面這四種距離問題，其中多以垂直為主，其實這已經(jīng)初步滲透了“最短距離”的思考模式.在后段的學習過程中，比如圓柱和圓錐的表面積求法中，學生了解了展開的思維.

雖有所涉及，但學生在此階段剛剛完成立體幾何的第一輪學習，因此借助此節(jié)課的內(nèi)容，通過“最短距離”多種問題的變換應用，強化學生“想圖、畫圖、識圖、解圖”的能力，重視圖形語言、文字語言、符號語言相互轉(zhuǎn)化的訓練.尤其重視對所畫的立體圖形、三視圖與真實圖形思維理解上的一致性.

3教學目標

（1）知識與技能：通過求解最短距離掌握“展開”的立體幾何距離問題基本解法.

（2）過程與方法：在展開過程中明確分類討論的思想以及截面還原精確性的把控，達成實際圖形和斜二測圖象的統(tǒng)一.

（3）情感態(tài)度與價值觀：通過最短距離的不同解法培養(yǎng)學生善于分析題意，富于聯(lián)想，以提高學生的空間想象能力，強化主動探索問題的精神和科學理性的思維方法.

4教學過程

4.1借典引入，提升興趣

其實早在1903年，就已經(jīng)有相應的數(shù)學謎題開始流傳，也就是著名的蜘蛛抓蒼蠅的故事.杜登尼（Dudeney，1857—1930）是19世紀英國知名的謎題創(chuàng)作者．“蜘蛛和蒼蠅”問題最早出現(xiàn)在1903年的英國報紙上，是杜登尼最有名的謎題之一．它對全世界難題愛好者的挑戰(zhàn)，長達四分之三個世紀．

4.2分類討論思想的滲透

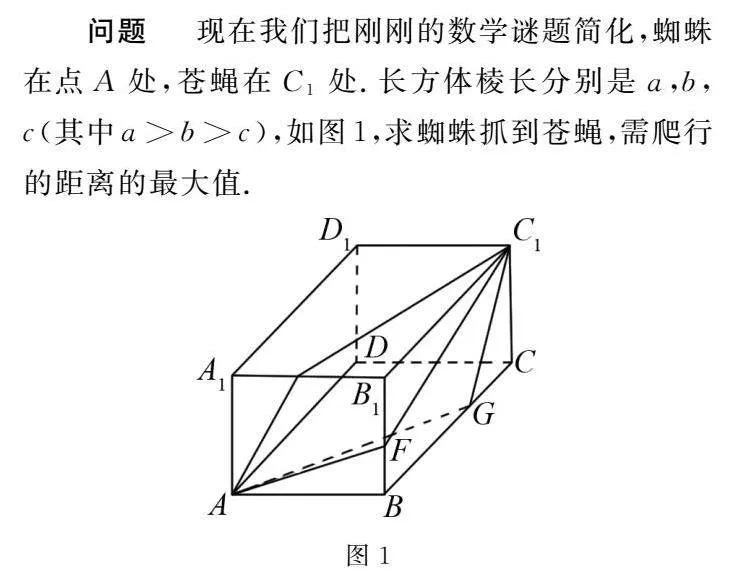
問題現(xiàn)在我們把剛剛的數(shù)學謎題簡化，蜘蛛在點A處，蒼蠅在C1處.長方體棱長分別是a，b，c（其中a＞b＞c），如圖1，求蜘蛛抓到蒼蠅，需爬行的距離的最大值.

題目分析通過此題提出展開的一大重點——分類討論.為了和之后的問題產(chǎn)生對應，引導學生從經(jīng)過棱的角度進行分類.

通過觀察，我們可以發(fā)現(xiàn)蜘蛛所經(jīng)過的棱共有6種可能，而其中兩兩具有對應關(guān)系.因此最后歸類為如下3種，如圖2.

立體問題平面化，將立體幾何的距離問題變?yōu)榍蟪鋈齻€矩形對角線長短進行比較的問題.

4.3截面還原，手腦統(tǒng)一

問題如圖3，在直三棱柱ABC-A1B1C1中，底面為直角三角形∠ACB=90°，AC=4，BC=CC1=2，P是BC1上一動點，則CP+PA的最小值是.

題目分析在這道題中，學生不需要像上題一樣討論棱的分類問題，已經(jīng)確定為BC1，難點設置在了是哪兩個面的展開上，由于圖象不如上道題完整，所以需要學生自己將截面進行補全，從而回顧立體幾何中公理三的推論——直線和直線外一點確定一個平面.

展開后，得到兩個三角形BC1A1和三角形BC1C，為了確定截面的具體形狀，從而算出每個三角形的三條邊長，明確特殊的角度，從斜二測畫法中還原為實際圖象后，再通過平面幾何求出線段距離.

4.4二維與三維的類比

問題如圖4，正方體ABCD-A1B1C1D1中棱長為a，點E為AA1的中點，在對角面BB1D1D上取點M，使AM+ME最小，其最小值為.

題目分析在之前的解析幾何中，學生學習過二維平面中求距離最短的方法——對稱.因此在本題中，進行二維到三維的遞進，根據(jù)圖形的對稱性，把AM+ME轉(zhuǎn)化為CM+ME，然后利用兩點之間線段最短求最小值.

解由對稱性可知AM=CM，

所以AM+ME=CM+ME，

觀察圖形，可知當E，M，C三點共線時，CM+ME即AM+ME取得最小值，

最小值為CE=2a2+（a2）2=32a.

5結(jié)語

在這節(jié)課中，希望學生借助立體幾何中的最短距離問題，體會數(shù)學“轉(zhuǎn)化與化歸”的思想，把看似不相關(guān)的兩個問題聯(lián)系在一起，便能夠“最”有應得.