渦軸發動機起動需求功率評估

摘 要：起動機主要作用是使渦軸發動機加速到點火轉速，起動需求功率評估是起動機設計或選型亟需解決的關鍵問題。本文采用多項式擬合對燃氣發生器轉速進行平滑處理。采用加速度方法計算渦軸發動機的靜力矩和阻力矩，得出起動扭矩。根據起動扭矩測量試驗結果，對計算方法的誤差進行評估，進而獲得渦軸發動機的最小所需扭矩和低溫天所需起動扭矩。最后基于渦軸發動機試驗數據，驗證了方法的可行性，評估出渦軸發動機起動所需功率，對渦軸發動機起動機設計或選型具有一定指導作用。

關鍵詞：渦軸發動機；項式擬合；加速度；起動扭矩；起動需求功率

中圖分類號：V 23" " " 文獻標志碼：A

起動過程是渦軸發動機工作情況極其復雜的過渡態過程之一。起動過程中的影響因素眾多，不同的環境溫度、壓力和點火時間均會影響發動機的起動性能，起動所需功率是保證發動機快速、可靠起動的關鍵因素，而在研制初期，如何確定起動需求功率是一個困擾已久的難題。

《航空發動機原理》提出了一個工程近似估算方法，計算時需要知道渦軸發動機的阻力矩、燃氣渦輪產生的扭矩和使燃氣發生器轉子加速的扭矩，其中根據經驗公式可得起動扭矩和燃氣渦輪產生扭矩隨燃氣發生器轉子轉速的變化關系，在該方法中，經驗系數的選取是關鍵，不同的經驗系數會使計算結果產生極大差別[1]。

本文對燃氣發生器轉速進行了多項式擬合，以A型渦軸發動機試驗數據為基礎，利用加速度計算方法得出凈力矩和阻力矩，并結合已有渦軸發動機起動扭矩測量試驗結果，評估加速度計算方法的誤差。進而分析B型渦軸發動機海平面標準天所需扭矩、最小所需起動扭矩和低溫天所需起動扭矩間的關系，采用類比的方法評估A型渦軸發動機起動所需功率。

1 渦軸發動機起動工作原理

渦軸發動機起動是將燃氣發生器轉速由靜止狀態加速到地面慢車狀態的過程。起動初期，燃氣渦輪產生的功率不足以將轉子加速到慢車轉速，起動過程必須利用起動裝置，通常將空氣渦輪起動機或起動發電機作為起動裝置，起動過程大致分為3個階段[2]。

第一階段，起動機接通，帶動燃氣發生器轉子轉動，并使其加速到點火轉速，燃氣渦輪開始做功，該階段發動機轉子由起動機帶轉。第二階段，燃燒室點火后，燃氣驅動燃氣渦輪做功，與起動機一起帶動燃氣發生器轉子轉動并加速，但是燃氣渦輪產生的可用功上升速度比壓氣機和其他附件消耗功的增加速度快，為了保證發動機能可靠起動并加快發動機起動，需要起動機繼續帶轉，直到起動機脫開，該階段發動機轉子由燃氣渦輪和起動機共同帶轉。第三階段，起動機脫開后，燃氣渦輪獨自帶動壓氣機和其他附件，使其加速到地面慢車狀態，在地面慢車狀態，燃氣渦輪所做功與壓氣機、動力渦輪以及其他附件消耗的功相等，該階段發動機轉子由燃氣渦輪單獨帶轉。

2 起動扭矩計算方法

為獲得發動機起動所需扭矩，需要知道發動機阻力矩（主要包括壓氣機葉片氣動扭矩、附件傳動扭矩以及克服軸承摩擦力所需的扭矩之和）、燃氣渦輪產生的扭矩、使燃氣發生器轉子加速的扭矩（簡稱凈力矩）以及它們與燃氣發生器轉速的變化關系。

2.1 數據處理方法

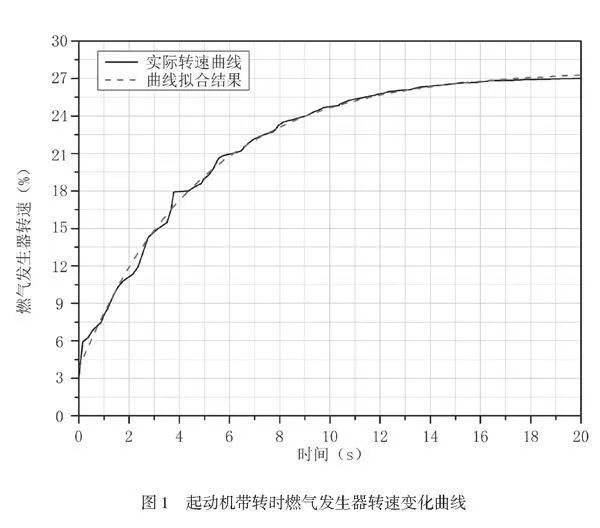
為提高發動機凈力矩和阻力矩計算精度，準確獲得燃氣發生器轉速（Ng）隨時間（t）的變化率（dNg/dt）是關鍵。試驗時，轉速數據采樣頻率一般較高，傳感器采集的轉速Ng變化波動較大且存在跳變點。對Ng隨時間的變化關系進行多項式擬合，進而可對數據中的跳變值進行平滑處理，不會影響變化趨勢，從而準確計算出Ng隨時間t的變化率。

2.2 凈力矩計算

凈力矩提供燃氣發生器轉子及其起動機帶動的其他轉子加速的力矩。發動機進行冷運轉時，起動機帶動燃氣發生器轉子轉動并達到平衡轉速，此時凈力矩為起動機輸出起動扭矩與發動機阻力矩之差，因此起動機脫開前的轉速變化率（如圖1所示）較好地反映了發動機凈力矩的大小。根據公式（1）對冷運轉時起動機脫開前凈力矩（ΔM）進行計算[3]。

（1）

式中：i為起動機轉速與燃氣發生器轉速的轉速比；j為起動機帶轉所有轉動件相對于起動機軸的有效轉動慣量。

2.3 阻力矩計算

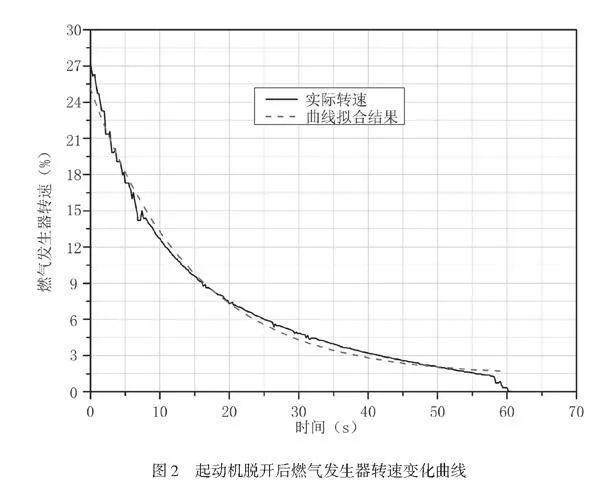
冷運轉時，起動機帶動燃氣發生器轉子轉動并加速至平衡轉速，起動機脫開后，燃氣發生器轉速在阻力矩的作用下逐漸下降，因此起動機脫開后的轉速變化率（如圖2所示）較好地反映了發動機阻力矩的大小。根據公式（2）對冷運轉時起動機脫開后阻力矩（MCT）進行計算[3]。

（2）

2.4 起動扭矩計算

發動機實際起動扭矩為發動機凈力矩和阻力矩之和，由公式（3）對冷運轉時的起動扭矩（MST）進行計算。

MST=?M+MCT （3）

再根據計算得到的起動扭矩和公式（4）對起動需求功率（PST）進行計算。

（4）

式中：ns為起動機轉速，r/min。

2.5 計算方法誤差分析

根據已有渦軸發動機起動扭矩測量試驗結果，處理試驗時的數據，按照上述計算方法獲得該渦軸發動機的起動扭矩。分析結果表明：起動扭矩的計算結果與試驗測量結果隨轉速的變化趨勢一致，同轉速下計算結果與試驗測量結果的誤差約為13%，小于工程評估方法。

3 起動需求功率評估

現根據上述計算方法，對渦軸發動機起動需求功率進行評估。

3.1 海平面標準天所需起動扭矩

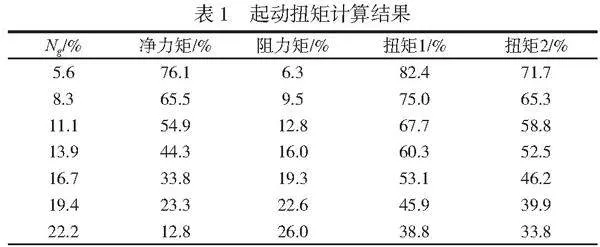
利用A型渦軸發動機海平面標準天的試驗數據對起動扭矩進行計算，具體計算步驟如下。1） 起動機帶轉時，燃氣發生器轉速Ng1隨時間變化的函數關系為Ng1（t），對Ng1（t）進行多項式擬合，結果如圖1所示；起動機脫開后，燃氣發生器轉速Ng2隨時間變化的函數關系為Ng2（t），并對Ng2（t）進行多項式擬合，結果如圖2所示。2） 根據擬合結果，可分別計算出（dNg1/dt）和（dNg2/dt），代入公式（1）和公式（2）計算出凈力矩（ΔM）和阻力矩（MCT）。3） 由公式（3）可計算出不同燃氣發生器轉速下的起動扭矩MST，并考慮該計算方法的誤差，計算結果見表1。表1中的扭矩1為起動扭矩計算值，扭矩2為考慮計算誤差后的起動扭矩。

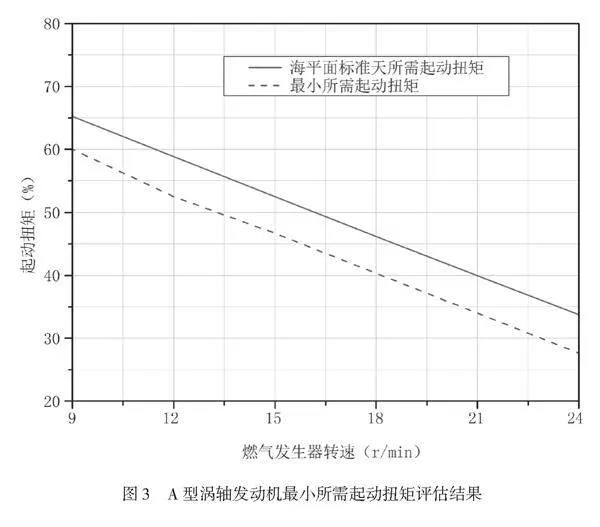
3.2 最小所需起動扭矩評估

最小所需起動扭矩是指滿足發動機最大起動時間要求的起動機輸出扭矩，停車無法在試驗中遇到剛好滿足起動時間的情況，本文擬采用類比的方法來評估發動機最小所需起動扭矩，方法如下：已知B型渦軸發動機的最小所需起動扭矩，計算出B型渦軸發動機海平面標準天所需起動扭矩相對于最小所需起動扭矩的增量，從而類比出A型渦軸發動機海平面標準天起動扭矩相對于最小所需起動扭矩的增量，得到A型渦軸發動機的最小所需起動扭矩。已知B型渦軸發動機在海平面標準天所需起動扭矩相對于其最小所需起動扭矩的增量為12.1%～22.2%，由此可類比得到A型渦軸發動機最小所需起動扭矩，類比結果如圖3所示。

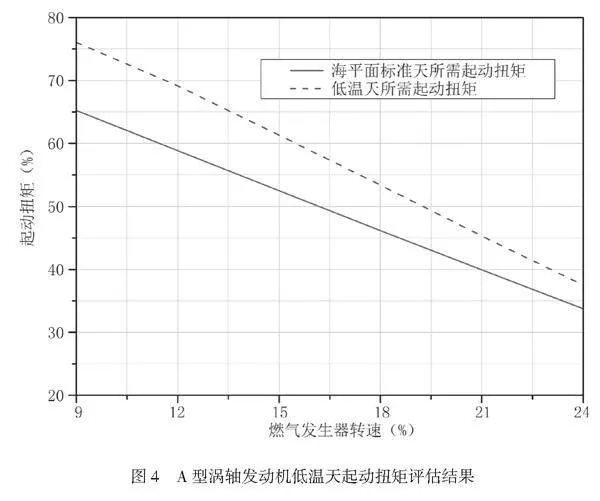
3.3 低溫天起動所需扭矩評估

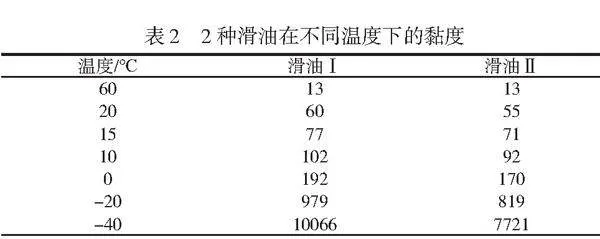
由滑油特性可知，隨著大氣溫度降低，滑油黏度急劇上升，轉子轉動需要克服的摩擦阻力矩明顯增大。以目前國內渦軸發動機常使用的兩種滑油Ⅰ、Ⅱ為例，不同溫度下的運動黏度見表2。

根據表2可知，當溫度下降時，滑油黏度急劇增加，以-40℃和15℃為例，滑油Ⅰ、Ⅱ的運動黏度分別相差130倍、108倍，因此低溫環境下發動機阻力矩會增加，所需起動扭矩將急劇增加。并且大氣溫度越低，空氣密度越大，同物理轉速條件下發動機進氣流量增大，帶動壓氣機轉動需要克服的空氣阻力矩也會增大。

根據上述分析可知，低溫環境下發動機所需起動扭矩會增大，已知A、B型渦軸發動機可靠工作的最低大氣溫度為-40℃，為保證A型渦軸發動機在工作環境溫度范圍內起動成功，采用與最小所需起動扭矩相同的類比方法，得出A型渦軸發動機的低溫天起動扭矩。

已知B型渦軸發動機在-40℃、不同轉速下的起動扭矩相對于海平面標準天起動扭矩的增量為11.1%～17.5%，由此可類比得出A型渦軸發動機-40℃下的起動扭矩，類比結果如圖4所示。

3.4 起動需求功率評估

綜上所述，本文通過計算得出A型渦軸發動機海平面標準天的起動扭矩，類比分析得出A型軸發動機最小所需扭矩和低溫天起動扭矩，根據公式（4）評估出了A型渦軸發動機起動需求功率。

4 結論

本文通過對燃氣發生器轉速進行多項式擬合，得出燃氣發生器轉速隨時間的變化率，病計算出渦軸發動機凈力矩、阻力矩和起動扭矩。結合A型渦軸發動機冷運轉試驗數據，利用本文計算方法得到了海平面標準天的起動扭矩，進而與起動扭矩測量試驗結果進行比較，評估計算誤差，采用類比分析得出A型渦軸發動機的最小所需起動扭矩和低溫天所需起動扭矩，并評估出A型渦軸發動機起動所需功率，得出以下3個結論。1） 本文采用的起動扭矩計算方法具有一定的可信度，計算結果與試驗結果變化趨勢一致，計算誤差約為13%，小于工程近似估算方法。2） 計算出了海平面標準天的起動扭矩，類比分析得到了A型渦軸發動機最小所需起動扭矩和低溫天起動扭矩，由此可評估出A型渦軸發動機起動所需功率。3） 本文評估方法對渦軸發動機研制初期起動機設計或選型具有重要指導意義。

參考文獻

[1]廉筱純，航空發動機原理[M].西安：西北工業大學出版社，2005.

[2]顧永根.《航空發動機設計手冊》第6冊[M].北京：航空工業出版社，2001.

[3]蔡建斌，尹澤勇，熊焰，等.一種確定燃氣渦輪發動機起動最小所需扭矩的工程方法[J].航空動力學報，2005（5）：736-739.