基于連續單元模擬的裝配式建筑彈塑性分析

摘 要：由于罕遇地震作用下的裝配式房屋結構有可能進入非線性狀態，因此準確模擬該非線性過程需要同時考慮裝配式房屋結構的幾何非線性、材料非線性和接觸非線性。幾何非線性一般通過變形梯度張量進行控制，材料非線性主要體現為裝配式房屋材料的塑性、損傷行為。針對上述復雜過程，本文采用Mises材料模型，結果表明，數值程序本構積分執行效率較高，且計算精度可滿足裝配式房屋結構彈塑性時程分析的要求。

關鍵詞：Mises材料模型；地震波；歐拉角；裝配式房屋

中圖分類號：TU 75 文獻標志碼：A

各學者對罕遇地震作用下的彈塑性動力時程分析方面的研究非常多。褚少輝等[1]對外掛裝配式墻板和內嵌裝配式墻板下的鋼框架水平側移剛度進行對比研究，得出內嵌裝配式墻板對鋼框架的側移剛度影響較大的結論。郭冬梅等[2]對多層裝配式鋼結構體系中的柱-柱連接節點在靜力性能與抗震性能方面研究的現狀與進展進行回顧，總結的內容包括連接類型、試驗、有限元計算等方面的研究，為裝配式鋼結構體系的柱連接的設計方法提供參考。孟娟等[3]針對裝配體式鋼結構住宅存在的問題，提出了新的梁柱與樓承板裝配方案，柱采用矩形管混凝土，為便于安裝，梁采用帶開孔的扁梁，樓板采用鋼筋桁架組合體系，梁柱節點可緩解節點位置焊接造成的應力集中，有利于提高安裝效率。閻紅霞等[4]采用實體單元模擬梁柱構件，對一幢弧形框架剪力墻結構進行彈塑性時程分析。汪大綏等[5]對梁柱構件應用自行開發的纖維單元模型，在纖維單元上部署多個附加積分點，對SRC框架結構在罕遇地震作用下的動力彈塑性時程進行分析，同時兼顧計算精度和數值效率。

1 彈塑性本構關系

根據輕鋼類裝配式建筑結構的薄壁幾何特征，實施整體彈塑性時稱分析時主要使用連續單元（殼單元）和空間梁單元進行分網。單元積分點應力調整采用J2流動塑性，本構積分采用彈性預測徑向修正策略，平衡迭代采用牛頓-拉普森算法。

2 有限元數值模型

2.1 遞推迭代格式

采用連續介質力學里的完全拉格朗日模型（TL）對結構在地震往復作用下的幾何構型演化進行描述，時間離散采用Newmark隱式積分格式，結合TL格式的有限元列式，建立參考初始時刻構型的平衡表達式，如公式（1）所示。

（1）

式中：α為時間積分所用的參數；M為一致型質量矩陣；Δu（l）為第l迭代步的位移增量向量；t+ΔtQ為t+Δt時刻模型承受的外荷載向量；t+Δtu（l）為t+Δt時刻第l迭代步模型的總位移向量；tu為t時刻的總位移向量；v為速度向量；a為加速度向量。

為反映裝配式建筑結構節點的裝配特征，數值模型中的異型裝配節點主要采用連續單元（殼單元）模擬[6]，其余部分采用空間梁單元模擬，通過轉換張量表示空間梁單元的局部坐標系隨構型演化對單元非線性剛度的影響，如公式（2）所示。

0hki=thnm（m=1，2，3；n=1，2...12） （2）

式中：thnm為t時刻單元局部坐標系下插值函數張量；與為轉換張量，近似由單元網格構型變化引起的歐拉角確定。

平衡迭代收斂判據的計算過程如公式（3）所示。

（3）

式中：FE-FT為公式（1）右端項計算的每個時間步迭代時的系統外荷載向量與內力向量差值，通過內力向量FT在迭代過程中不斷更新，ΔQ為公式（1）右端項計算的每個時間步迭代前的系統荷載向量與內力向量差值Norm2的歐式范數；δcrt為殘差判據值，取1×10-6。

2.2 材料參數和抗震性能化設計

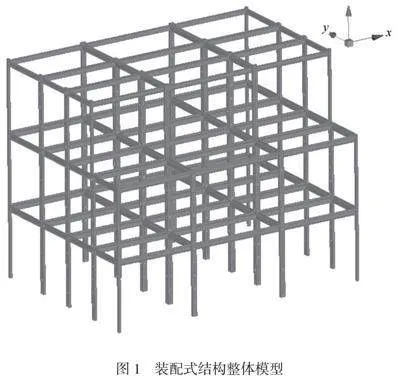
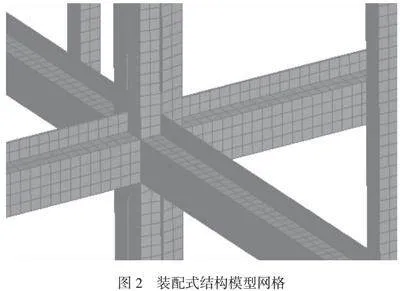
由于算例模型中的構件細部幾何特征較為復雜，單純選用梁桿系單元不能準確模擬構件的非線性行為，因此應該采用連續單元進行分網，如圖1和圖2所示，圖1為整體分網，圖2為細部分網，實體單元和殼單元在數值格式上均屬于連續單元，本文采用全積分的殼單元模擬型鋼構件，與采用空間梁單元模擬不同，殼單元能夠準確反映各部件的裝配關系。材料采用J2流動塑性，材料參數如下。

**M2；Default MATERIAL

**

*MATERIAL， NAME=M2；Default MATERIAL

*Damping，alpha=1.066， beta=0.000210

*Density

7.85e-09，

*Elastic

210000.，0.3

*Plastic

215.，" " "0.

245.， 0.0235

294.， 0.0474

374.， 0.0935

437.，" 0.138

480.，" "0.18

結構阻尼采用Rayleigh阻尼模式，通過第一振型對應的周期和基頻周期的20%回代計算確定質量阻尼系數和剛度阻尼系數，分別為1.066和0.000210。在結構模型基底節點施加Y方向方向的地震加速度，地震波工況主要是CPC_TOPANGA CANYON_16_nor波，持續時間分別為44s，通過編制數據轉換程序，創建地震波的幅值文件，數據轉換過程如下。

clc；

clear；

load wave_02.txt；

aca=wave_01（：，2）；

ac=aca’；

[m，n]=size（ac）

for i=1：2780

t1（i）=（i-1）*0.02；

end

[m，n]=size（t1）

plot（t1，ac）；

fid3=fopen（‘data2.txt’，’w’）；

for i=1：2421

for j=1：2

if j==2

fprintf（fid3，’%.4f，＼n’，ac（i））；

else

fprintf（fid3，’%.4f，’，t1（i））；

end

end

end

fid4=fopen（‘data3.txt’，’w’）；

for i=1：2421

for j=1：2

if j==2

fprintf（fid4，’%.4f＼n’，ac（i））；

else

fprintf（fid4，’%.4f ‘，t1（i））；

end

end

end

3 計算結果和分析

3.1 數值模型迭代歷程

對數值模型進行平衡迭代，在地震波初始激勵階段的平衡迭代中，不平衡力向量歐式范數收斂殘差值遠大于后期激勵階段，但不平衡力殘差值下降率較大，能在迭代次數15步以內滿足收斂判據規定的平衡條件，說明本文集于連續單元數值模型的收斂性良好。

3.2 計算結果

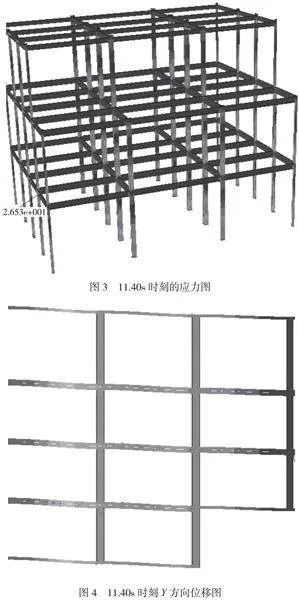
圖3是模型Mises應力云圖，在地震波峰值時刻（11.40s左右）的最大Mises應力為26.53MPa，與Q235鋼材的初始屈服強度235MPa，相差較遠，反映模型未進入塑形狀態。

Y方向位移圖如圖4所示。位移形式主要表現以結構整體剛體平移為主（基底隨地面運動而動），第一層頂部節點位移為382.5mm，第二層頂部節點位移為層間位移角約為383.8mm，層間位移角約為1/2307，遠小于彈塑性位移角限值1/50。說明該結構在CPC_TOPANGA CANYON_16_nor地震波作用下未進入塑形狀態。

本文基于連續單元模擬的非線性時程數值方法，迭代效率較高，數值精度可靠，對復雜裝配節點的適應性良好，可滿足裝配式建筑結構大震彈塑性計算的要求。

裝配式建筑結構在工地現場具有較多的裝配環節，對很多新型裝配節點方案來說，由于現場裝配質量控制受到多種因素的影響，因此新型裝配節點的配合面很難做到完全充分接觸，在地震的往復作用下接觸狀態會適時變化，大震彈塑性時程計算須能反映這個響應過程，本文算例對這類裝配節點采用連續單元進行分網，連續單元的面特征可以滿足充分接觸狀態判斷算法的要求，這在接觸非線性數值計算里面也最常用的。

大震彈塑性可分為靜力彈塑性和動力彈塑性兩種類型，從房屋高度的角度來看，輕鋼類裝配式建筑結構可只采用靜力彈塑性方法，但從裝配節點的特異性角度來看，結構在高度方向的剛度變化較為復雜，采用動力彈塑性方法的適應性更強。

裝配式建筑結構的節點構造較為復雜，單純采用梁桿系單元難以反映實際構件的幾何特征，因此采用連續單元離散部分構件是不可或缺的，在本構積分點層面上進行彈塑性分析，計算量通常較大，研究合理的本構積分方案至關重要，根據鋼材的流動塑性和硬化特征，算例采用金屬材料的彈塑性模型的收斂效果良好。

4 結論

當面對罕見地震作用時，裝配式房屋結構可能會進入非線性狀態，這通常伴隨塑性變形和較大的位移尺度。因此，在強震作用下，需要考慮材料非線性、幾何構型變化以及接觸狀態的變化對剛度的影響，剛度矩陣需要適時更新。這種情況綜合體現了材料非線性、幾何非線性和接觸非線性，與抗震性能設計密切相關[7]。

裝配式房屋結構主要使用鋼和混凝土兩種材料，其中輕鋼裝配式房屋主體結構采用鋼材，而混凝土材料的塑性、損傷和拉壓等性質較為復雜。因此，模擬混凝土材料的本構模型需要考慮塑性演化和損傷演化，通常采用連續損傷法則，以提高計算效率。由于鋼材性質較為均勻，因此本文所采用的J2流動塑性本構策略能夠較好地反映這個特征。

在裝配式建筑結構中，構件、裝配節點和傳統建筑存在較大的不同。因此，單純采用梁桿系單元無法準確還原構件和裝配式節點的幾何特征。為了解決這個問題，采用連續單元進行分網是一種可行的方法。盡管會增加計算量，但對大多數輕型鋼結構的裝配式建筑來說，通常不超過3層，結構主構件數量有限，因此采用連續單元（主要是實體單元和殼單元）進行模擬是可行的。

算例模型基于連續單元進行分網，能夠適應裝配式建筑結構的幾何特征，同時也能準確考慮罕見地震作用下的幾何非線性和裝配節點接觸非線性。此外，連續單元的本構積分模型較為豐富，能夠滿足大震彈塑性時程計算中材料非線性的要求。

盡管算例計算結果表明，關鍵構件和非關鍵構件均保持彈性，但本文的數值模型仍然適用于相關構件進入非線性狀態的情況，特別是層數較多的裝配式建筑結構。然而，需要注意的是，隨著自由度增加，求解所需的計算時間可能也會增加。

參考文獻

[1]褚少輝，趙士永，劉亞賢.村鎮裝配式住宅鋼結構體系抗震性能分析研究[J].粉煤灰綜合利用，2017（6）：5.

[2]郭冬梅，王元清，伊永成.裝配式多層鋼結構柱-柱連接的研究與展望[J].交通科技與經濟，2019，21（6）：6.

[3]孟娟，張辰，楊睿，等.裝配式鋼結構住宅體系的優化研究[J].建筑結構，2019（1）：5.

[4]閻紅霞，楊慶山，張麗英.ABAQUS在超高層結構動力彈塑性分析中的應用[J].震災防御技術，2010，5（1）：108-115.

[5]汪大綏，李志山，李承銘，等.復雜結構彈塑性時程分析在ABAQUS軟件中的實現[J].建筑結構，2007，37（5）：92-95.

[6]王學濱，薛承宇，岑子豪.基于點-單元接觸模式的水平巖層運動連續-非連續方法模擬[J].山東科技大學學報（自然科學版），2022，41（6）：40-49.

[7]李曉飛，薛曉峰，吳彥霖.蘭州新區保障住宅裝配式鋼結構的抗震性能分析[J].特種結構，2019（4）：6.