面向在線多標簽分類的多核算法

摘 要：

近年來，多核方法已被證實在很多領域上有著比單核更好的性能。然而，現有的在線多標簽分類算法大多采用單核方法，并且依賴于離線的核函數選擇過程。為了克服這些問題并提升分類性能，提出了一種在線多核多標簽分類算法（online multi kernel multi-label classification，OMKMC）。具體而言，OMKMC將多個核分類器及其權重系數的學習建模成一個非凸優化問題，使用交替最小化方法求解這一問題，推導出了核分類器及其權重系數的閉式更新公式。此外，OMKMC還引入了孤立核以解決大規模數據上的計算問題。在八個公開數據集上的實驗表明，相較于其他幾種先進多標簽分類算法，OMKMC在多項性能指標上均有優勢，證明了OMKMC是有效的。

關鍵詞：多標簽分類；多核學習；非凸優化；在線學習

中圖分類號：TP391"" 文獻標志碼：A""" 文章編號：1001-3695（2024）12-017-3651-07

doi： 10.19734/j.issn.1001-3695.2024.04.0125

Multi kernel algorithm for online multi-label classification

Tang Chaoyang， Zhai Tingting， Zheng Yixian

（College of Information Engineering， Yangzhou University， Yangzhou Jiangsu 225127， China）

Abstract：

In recent years， researchers have shown that multi-kernel methods outperform single-kernel methods in various domains. However， existing online multi-label classification algorithms mostly adopt single-kernel approaches and rely on offline kernel function selection processes. To address these issues and improve classification performance， this paper proposed an online multi-kernel multi-label classification algorithm （OMKMC）. Specifically， OMKMC modeled the learning of multi kernel classifiers and their weight coefficients as a non-convex optimization problem， solving this problem using an alternating minimization approach， which derived closed-form update formulas for kernel classifiers and their weight coefficients. Additionally， OMKMC introduced an isolation kernel to handle computational challenges on large-scale data. Experiments on eight public datasets show that OMKMC outperforms several advanced multi-label classification algorithms in various performance metrics， proving its effectiveness.

Key words：multi-label classification; multi kernel learning; non-convex optimization; online learning

0 引言

核方法是機器學習領域中的重要方法，廣泛用于各種非線性預測任務中［1，2］。一方面，核方法利用核函數隱式地將數據映射到一個高維特征空間中，并在此空間中進行學習和預測，另一方面，核方法利用核技巧避免顯式地計算高維的特征映射。現有的核方法可以分為單核方法和多核方法。單核方法的性能受限于數據的特征分布，并不能很好地處理具有多源異構特征的數據［3］，而且其核函數的參數選取過程較為復雜，往往需要借助于交叉驗證或者額外的數據。相比之下，多核方法通過結合多個核函數，能夠較好地表示多源異構數據，并且能學習不同核函數的組合方式，自動調整核函數的權重，以獲得更優的模型性能。

近年來，出現了很多有效的多核學習方法，例如基于Boosting的多核組合方法［4］、基于Nystrm的多核學習方法［5］、基于引力策略的多核學習方法［6］、基于深度學習的多核學習方法［7］等。盡管上述多核模型有著比單核模型更好的性能，但是它們在學習過程中需要將所有的數據都存儲在內存中才能進行學習，因此并不適用于數據持續增長的數據流環境。

鑒于此，Jin等人［8］將多核學習與在線學習結合，首次提出了在線多核學習方法，該方法通過在線的方式實現了核分類器及其權重系數的同步更新，使得多核學習可以適用于數據流環境，但該方法在使用流行的高斯核作為核函數時具有可拓展性差的問題。Shen等人［9］首次利用隨機傅里葉特征技術［10］來實現可拓展的在線多核學習，通過一個專家建議算法Hedge［11］對核分類器進行加權組合。當預定義的核集中包含大量的核時，Ghari等人［12］利用核之間的相似性構造了反饋圖，借助于圖的反饋信息，從所有核中選擇一個子集，實現對不相關核的裁剪，以減輕多核學習的計算負擔。

盡管在線多核學習已經取得了一定的研究進展，但幾乎所有研究都集中在單標簽分類或回歸任務上，對于多標簽分類的研究非常少。多標簽分類在現實世界中具有非常廣泛的應用，例如在文本分類［13］、圖像分類［14］、生物信息學［15］以及醫學診斷［16］等領域。相比于單標簽分類，在多標簽分類中，每個實例與多個標簽相關聯，且標簽之間可能存在相關性，其預測任務是為任意輸入的實例輸出與之相聯系的所有標簽。因此，多標簽分類通常是比單標簽分類更難的任務，需要開發專門的算法和技術。根據應用場景的不同，多標簽分類可以分為離線多標簽分類和在線多標簽分類，其中在線多標簽分類是近年來興起的一個重要研究方向，更加適用于社交媒體、電商推薦、新聞推薦等實時性強、數據動態性強的應用場景。

盡管目前已有幾個在線多標簽分類算法被提出，但這些算法都是單核的，且依賴于離線的核函數選擇程序。Qiu等人［17］提出了一種基于核極限學習機的半監督在線多標簽分類算法，該算法在構造極限學習機的輸出函數時，使用核函數代替隱藏層映射，并將半監督極限學習機［18］調整到數據流的場景中。Zhai等人［19］提出了一族被動主動的在線多標簽分類算法，該族算法旨在學習標簽得分和閾值的預測器，使得相關標簽的得分在閾值之上，而閾值又在無關標簽的得分之上，該目標被建模為一個包含兩個線性約束的凸優化問題，通過求解KKT條件得到問題的最優解。之后，Zhai等人［20］又提出了一個聯合優化閾值與標簽評分模型的框架，將多標簽分類問題建模為一個包括L個線性約束的凸優化問題，其中L是標簽的數量，并將其轉換為一個無約束問題，通過一階在線梯度下降法或二階自適應鏡像下降法進行求解。其中，Zhai等人［20］的一階自適應標簽閾值算法能與核進行結合，表現出很強的性能。

基于以上分析，為了克服傳統的基于批量學習的核方法在選擇核函數時所面臨的困難，同時彌補現有在線多核方法在多標簽領域研究的不足，本文提出了一種全新的在線多核多標簽分類算法。本文方法通過在線地學習多個核分類器，并動態地分配每個核分類器的貢獻系數，不僅能免去離線選擇核函數的煩瑣步驟，而且有效地提升了多標簽分類任務的性能。本文的貢獻如下：

a）將核分類器及其權重系數的學習建模成一個非凸優化問題，通過交替最小化方法求解這一問題，推導出了核分類器以及組合系數的閉式更新公式。

b）為了緩解在線核學習所面臨的核災難問題，本文引入孤立核［21］，該核函數具有顯式的特征映射，使得學習模型可以在新的特征空間中直接通過向量來表示，實現了本文算法的高效運行。

c）在八個不同領域的公開數據集上，與多種先進的多標簽分類算法相比，本文算法在多項性能指標上均有優勢。

1 符號表示和問題設定

為處理大規模數據，本文算法采用孤立核［21］。孤立核具有一個顯式的特征映射，借助于該映射，（x）可以直接用向量表示，從而每個模型都可以用向量表示，因此無須保存支持向量。孤立核的核心思想是，隨機選取φ個數據樣本點，以數據樣本點為基準將數據空間切分為φ個子空間，當實例x到來時，判斷x會落入到哪個子空間，落入的空間標記為1，其余空間記為0，因此，（x）可以表示成一個由0和1組成的長度為φ的向量。通常要隨機進行多次子空間的劃分，劃分次數記為t，最終數據點x經過孤立核映射變成一個長度為tφ的向量，即（x）∈{0，1}tφ。

孤立核已經在二分類、聚類和異常檢測等領域得到了應用，但根據調查，目前尚未有研究在多標簽學習領域應用孤立核。因此，本文的研究不僅豐富了孤立核的應用范疇，也為多標簽學習提供了一種新的思路和方法。

4 實驗

4.1 實驗環境以及實驗數據集

本文所使用的實驗環境為CPU為Intel Core i7-10700，內存大小為16 GB。本文的編程環境為MATLAB R2018b。

本文選擇了來自多個領域的8個公開數據集，選擇這些數據集主要基于以下幾點考慮：

a）多領域覆蓋：這些數據集覆蓋了生物、音樂、圖像、文本、視頻和醫藥等多個不同的領域。選擇來自不同領域的數據集有助于驗證本文方法的廣泛適用性。

b）規模多樣性：所選數據集具有不同的規模，從小規模到大規模的數據集都有涵蓋。通過在規模不同的數據集上進行實驗，可以全面評估本文方法在不同數據規模下的表現。

c）標準數據集選擇：這些數據集都是多標簽分類研究領域中常用的數據集，選擇這些標準數據集不僅能夠方便與其他研究的對比，而且能夠確保實驗結果的通用性。

使用的所有數據集都可以在如下的網站上進行下載（https：//www.uco.es/kdis/mllresources/），數據集信息如表1所示。

4.2 評估指標

本文采用7個常見的多標簽分類評估指標來評價算法的性能，分別是精確率（precision，P）、召回率（recall，R）、F1度量、MacroF1、MicroF1、漢明損失（Hamming loss，HL）以及排序損失（ranking loss，RL），它們的計算公式為

F1=2×P×RP+R（20）

其中：N是評估的測試樣本數目；精確率是指被正確預測為正例的樣本數占所有被預測為正例的樣本數的比例；召回率是指被正確預測為正例的樣本數占真實正例的樣本數的比例；F1度量值是精確率和召回率的調和平均值，用于綜合評估模型的性能。這三個性能指標的值越大越好。

MacroF1=1Q∑Qj=12×tpj2×tpj+fpj+fnj（21）

MicroF1=2×∑Qj=1tpj∑Qj=1（2×tpj+fpj+fnj）（22）

其中：Q表示標簽數量；tpj、fpj和fnj分別代表第j個標簽的真陽性、假陽性和假陰性的實例個數。以上兩種指標越大越好。

HL=1N×Q∑Ni=1|Y^iΔYi|（23）

RL=1N ∑Ni=1 ∑j∈Yi，k∈YiI［h（xi， j）≤h（xi，k）］|Yi|×|i|（24）

其中：Δ指的是兩個集合的對稱差；h（xi， j）表示在實例xi的標簽j上的模型預測分數。漢明損失衡量被錯誤預測的標簽的比例，排序損失衡量多個標簽排序時的性能，這兩個性能指標值越小越好。

4.3 對比算法

本文根據數據集的規模大小采取了不同的策略，對于表1中的Gpositive、CHD-49、Emotions、Yeast和Scene這五個規模較小的數據集，本文算法采用多個高斯核作為預定義的核，記該算法為OMKMC-GK，并與如下4個基線算法進行對比：

FALT-GK［20］：一階自適應標簽閾值算法，采用單個高斯核處理非線性分類。

OMKMC-GK-EW：OMKMC-GK的一個退化版本，也是多核方法，但是為每個核分類器分配相同且固定的權重系數，僅更新核分類器，不更新核權值。即對于t∈［T］，m∈［M］，βt，m=1/M。

CLML［26］：該算法利用標簽和實例的相關信息來學習多標簽分類的共同特征和特定于標簽的特征。

CMLL［27］：通過對標簽和特征的兩個嵌入空間進行聯合學習，改進了現有的緊湊學習方法。其中k-CMLL算法是CMLL算法的核化擴展版本。

選擇這些算法作為對比算法主要基于以下考慮：

a）與原單核算法的對比：本文將原單核算法擴展為多核方法。因此，本文選擇了單核方法FALT作為基準模型。通過與FALT的比較，可以驗證本文方法在原單核方法基礎上的改進和提升。

b）權重更新方法的有效性：引入退化的多核方法OMKMC-EW作為基線模型。OMKMC-EW為每個核分類器分配相同且固定的權重系數，通過與OMKMC-EW的比較，可以有效地評估本文權重更新方法的有效性。

c）與先進方法對比：CLML和CMLL是當前多標簽分類領域中的前沿方法，與它們進行對比可以全面評估本文方法的性能表現。

對于表1中的Enron、Tmc2007、Mediamill這三個規模較大的數據集上，本文算法采用多個孤立核作為預定義的核，算法記為OMKMC-IK，并與如下5個基線算法進行對比：

FALT-IK：采用單個孤立核的一階自適應標簽閾值算法。

FALT-M-IK：使用多個孤立核，利用每個核對應的顯式特征映射m得到實例x的新的向量表示（x），然后將所有的向量串聯起來得到融合的特征表示［1（x），…，M（x）］，作為線性的FALT算法的輸入。

OMKMC-IK-EW：將OMKMC-GK-EW中的高斯核換成孤立核得到的算法。

其余兩個基線算法分別是CLML和CMLL，已在上文簡單介紹過。

4.4 實驗設定

為了增強本文算法的收斂性，允許算法在整個訓練集上遍歷10次，其中前幾次用于對所有的單核多標簽模型進行初始化，后幾次用于執行交替最小化策略來更新多核多標簽分類模型。剩余在線算法FALT也允許遍歷10次。

對于多核學習問題來說，如何選擇核的個數及種類在目前來說沒有一個統一的理論標準，但是本文方法可以自適應地調整各個核函數的權重，從而無須過多地關注核函數的選擇，僅需一個預定義的核集。具體來說，本文算法OMKMC-GK共選用了11個高斯核，其表達式為Euclid Math OneKAp（xi，xj）=exp（－‖xi－xj‖22δ2），其中所選取的11個核參數δ2分別是{2－5，2－4，…，25}，正則項參數λ的搜索區間是［10－10，10－5］，兩個學習率α和η的搜索區間是［2－5，25］。使用孤立核的算法OMKMC-IK選用log2（n/2）」－2個孤立核，其中n是訓練樣本的數量，每個孤立核的采樣次數t均設置為100，每次采樣的樣本量φ的取值分別是{23，24，…，2log2（n/2）」}，算法其余參數的設定與OMKMC-GK相同。

基線對比算法中，FALT-GK的核參數δ2從OMKMC-GK的預定義核集中選取最優的那個，FALT-IK使用的孤立核從OMKMC-IK的預定義核集中選擇最優的那個。對于其余的多核算法，其預定義的核集與本文的算法設置相同。CLML和CMLL這兩種算法的參數是根據原論文中建議的參數設置來選擇的。

通過交叉驗證結合網格搜索找到最優參數，一旦找到最優參數，對訓練數據集進行 20 次隨機排列以學習模型，并將學習后的模型在測試數據進行評估，將這20次評估的平均值作為實驗結果。

4.5 實驗結果分析

表2～9記錄了不同算法在每個數據集上的性能指標值，其中括號內的為標準差，采取配對t檢驗，在95%置信水平下，每個指標的最佳結果及其可比結果用粗體表示。其中，基線對比算法k-CMLL在測試Tmc2007和Mediamill這兩個數據集時內存溢出，無法呈現測試結果，該方法并不適用于大規模數據集。

從表2～6可以看出，在幾乎所有的性能指標上，本文算法OMKMC-GK都顯著優于采用固定權重系數的OMKMC-GK-EW。這表明為每個核分類器分配合適的權重系數是非常重要的，也表明本文算法的核分類器權重系數的更新

方法是有效的。與經過核參數精細挑選的FALT-GK相比，OMKMC-GK在Gpositive、CHD-49、Emotions、Scene和Yeast這五個數據集上都具有競爭優勢，這表明了本文所提出的多核方法是有效的，同時OMKMC-GK還省去了選取核參數的煩瑣步驟。與其余兩個算法CLML和k-CMLL相比，本文算法的性能指標在這五個數據集上都具有顯著優勢。

綜上，在高斯核上，本文方法的綜合性能優于對比算法，在絕大多數性能指標上都能取得具有競爭力的結果。

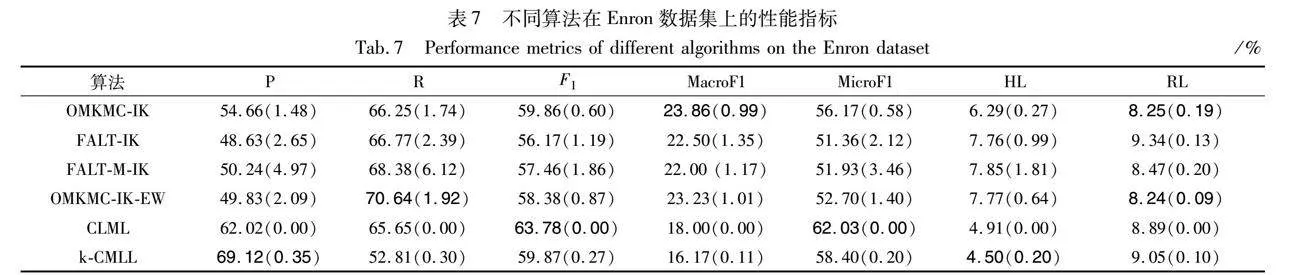
從表7～9可以看出，與經過核參數精心挑選的FALT-IK相比，本文算法OMKMC-IK在Enron、Tmc2007和Mediamill這三個數據集上，幾乎所有的指標都優于FALT-IK。與多核特征融合的算法FALT-M-IK相比，在所有數據集上，本文算法在多數指標上都有領先，這表明雖然都是使用了多個核函數，但是對多個核分類器進行更新的方法是有效的。與采用固定權重系數的算法OMKMC-IK-EW相比，本文算法在所有數據集上的評估指標幾乎都優于OMKMC-IK-EW，這再一次證明了本文方法更新核分類器的權重系數是有效的。與離線算法CLML相比，本文算法在Tmc2007數據集上有顯著優勢，在Enron和Mediamill數據集上各有領先，具有競爭優勢。

綜上，分析表2～9可以得出，無論是在高斯核還是在孤立核上，本文方法的綜合性能都優于對比方法，在大部分性能指標上都能取得具有競爭力的結果，這充分地驗證了本文所提出的多核方法是有效的。

對于3個大規模數據集，本文將高斯核和孤立核在OMKMC算法中的性能進行了全面比較。除了常規的性能指標外，還特別增加了訓練時間這一指標，以展示不同核函數在時間效率上的差異。表10記錄了Enron和Tmc2007數據集上的性能指標和訓練時間。此外，由于Mediamill數據集在高斯核的方法上超出了本文所用設備的計算資源限制，所以無法呈現該數據集的實驗數據。

從表10可以看出，孤立核和高斯核在這兩個數據集上的性能表現大致相當，盡管在部分性能指標上，孤立核略遜于高斯核。然而，在訓練時間方面，孤立核顯著優于高斯核。例如，在Tmc2007數據集上，孤立核的訓練時間是101.25 s，高斯核是2 091.54 s，相差20倍左右。因此，孤立核方法在處理大規模數據集時，不僅能夠保持較高的性能，還能顯著提高時間效率，這使得孤立核在大規模數據集的應用中更具實際應用價值。

最后，為了驗證本文方法在實例上的應用結果，使用南京大學機器學習與數據挖掘研究所公開的自然圖像數據集（https：//www.lamda.nju.edu.cn/data_MIMLimage.ashx）。該數據集共有2 000張圖片，分為沙漠、山脈、海洋、落日、樹木5種標簽類別。每張圖片都與一個、兩個或三個標簽相關聯。本文從測試集中隨機選取了6張圖片，運行本文方法并將預測結果與圖片的真實標簽進行對比，圖1展示了這些圖片及其預測結果，圖片下方的文字為預測結果。

從圖1可以看出，本文方法在實例上的分類結果比較準確，除了圖（f）未能預測到“沙漠”標簽以外，其余圖片全部預測正確。圖（f）預測失敗可能是因為“沙漠”標簽出現頻次較低，導致模型未能充分學習該特征，進而在識別該標簽時表現不佳。

通過上述實例分析可以看出，本文方法在多標簽分類任務中的應用效果良好，大多數標簽均能準確預測。

5 結束語

本文提出了一種在線多核多標簽分類算法，具體來說，將多個核分類器及其權重系數的學習建模成一個非凸優化問題，通過使用交替最小化方法推導出了核分類器及其權重系數的閉式更新公式。在八個公開數據集上的實驗表明，本文算法在多項性能指標上均有優勢。

雖然在多核學習中，核函數的選取并沒有一個統一的理論標準，但是本文方法不需要通過離線的方法來確定最優的核分類器組合方式，而是從預定義的核集中以在線地方式篩選出性能較優的核分類器，并將它們進行加權組合來進行最終的預測，這種方法不僅省去了煩瑣的核函數選擇步驟，而且能夠充分利用不同核函數捕捉數據特征的優勢，提升整體的分類性能。這充分體現了本文方法的有效性和實用性。

此外，在實驗部分，本文將多個核函數得到的特征進行簡單的拼接，得到了多標簽數據集的一種融合特征表示方法，在融合后的數據集上運行多標簽算法，取得了比單核方法更好的效果。然而，目前還存在著許多先進的特征融合方式，因此在未來的研究中，可以在多核特征融合的方向上作進一步探索。

參考文獻：

［1］Tang Jingjing， Hou Zhaojie， Yu Xiaotong， et al. Multi-view cost-sensitive kernel learning for imbalanced classification problem ［J］. Neurocomputing， 2023， 552： 126562.

［2］Wu Wenhui， Hou Junhui， Wang Shiqi， et al. Semi-supervised adaptive kernel concept factorization ［J］. Pattern Recognition， 2023， 134： 109114.

［3］Gonen M， Alpaydm E. Multiple kernel learning algorithms ［J］. Journal of Machine Learning Research， 2011， 12： 2211-2268.

［4］曾禮靈， 李朝鋒. 結合Boosting方法與SVM的多核學習跟蹤算法 ［J］. 計算機工程與應用， 2018， 54（13）： 203-208. （Zeng Li-ling， Li Chaofeng. Multiple-kernel learning based object tracking algorithm with Boosting and SVM ［J］. Computer Engineering and Applications， 2018， 54（13）： 203-208.）

［5］Wang Ling， Wang Hongqiao， Fu Guanyuan. Multi-Nystrm method based on multiple kernel learning for large scale imbalanced classification ［J］. Computational Intelligence and Neuroscience， 2021， 2021： 9911871.

［6］Yang Mengping， Wang Zhe， Li Yangqiong， et al. Gravitation ba-lanced multiple kernel learning for imbalanced classification ［J］. Neural Computing and Applications， 2022， 34（16）： 13807-13823.

［7］Rebai I， Ayed Y， Mahdi W. Deep multilayer multiple kernel learning ［J］. Neural Computing and Applications， 2016， 27（8）： 2305-2314.

［8］Jin Rong， Hoi S C H， Yang Tianbao. Online multiple kernel lear-ning： algorithms and mistake bounds ［C］// Proc of the 21st International Conference on Algorithmic Learning Theory. Berlin： Springer， 2010： 390-404.

［9］Shen Yanning， Chen Tianyi， Giannakis G B. Random feature-based online multi-kernel learning in environments with unknown dynamics ［J］. Journal of Machine Learning Research， 2019， 20（1）： 773-808.

［10］Rahimi A， Recht B. Random features for large-scale kernel machines ［C］// Proc of the 21st Annual Conference on Neural Information Processing Systems. New York： Curran Associate Inc.， 2007： 1177-1184.

［11］Freund Y， Schapire R. A decision-theoretic generalization of on-line learning and an application ［J］. Journal of Computer And System Sciences， 1997， 55（1）： 119-139.

［12］Ghari P M， Shen Yanning. Graph-aided online multi-kernel learning ［J］. Journal of Machine Learning Research， 2024， 24（1）： 751-794.

［13］田雨薇， 張智. 基于標簽推理和注意力融合的多標簽文本分類方法 ［J］. 計算機應用研究， 2022， 39（11）： 3315-3319， 3326. （Tian Yuwei， Zhang Zhi. Multi-label text classification method based on label reasoning and attention fusion ［J］. Application Research of Computers， 2022， 39（11）： 3315-3319， 3326.）

［14］楊敏航， 陳龍， 劉慧， 等. 基于圖卷積網絡的多標簽遙感圖像分類 ［J］. 計算機應用研究， 2021， 38（11）： 3439-3445. （Yang Minhang， Chen Long， Liu Hui， et al. Multi-label remote sensing ima-ge classification based on graph convolutional network ［J］. Application Research of Computers， 2021， 38（11）： 3439-3445.）

［15］Sun Liang， Zu Chen， Shao Wei， et al. Reliability-based robust multi-atlas label fusion for brain MRI segmentation ［J］. Artificial Intelligence in Medicine， 2019， 96： 12-24.

［16］Wang Xin， Wang Jun， Shan Fei， et al. Severity prediction of pulmonary diseases using chest CT scans via cost-sensitive label multi-kernel distribution learning ［J］. Computers in Biology and Medicine， 2023， 159： 106890.

［17］Qiu Shiyuan， Li Peipei， Hu Xuegang. Semi-supervised online kernel extreme learning machine for multi-label data stream classification ［C］// Proc of International Joint Conference on Neural Networks. Piscataway， NJ： IEEE Press， 2022： 1-8.

［18］Huang Gao， Song Shiji， Gupta J N D， et al. Semi-supervised and unsupervised extreme learning machines ［J］. IEEE Trans on Cybernetics， 2014， 44（12）： 2405-2417.

［19］Zhai Tingting， Wang Hao. Online passive-aggressive multilabel classification algorithms ［J］. IEEE Trans on Neural Networks and Learning Systems， 2023， 34（12）： 10116-10129.

［20］Zhai Tingting， Wang Hao， Tang Hongcheng. Joint optimization of scoring and thresholding models for online multi-label ［J］. Pattern Recognition， 2023， 136（109）： 167.

［21］Ting Kaiming， Wells J R， Washio T. Isolation kernel： the x factor in efficient and effective large scale online kernel learning ［J］. Data Mining and Knowledge Discovery， 2021， 35（6）： 2282-2312.

［22］Hoi S C H， Jin Rong， Zhao Peilin， et al. Online multiple kernel classification ［J］. Machine Learning， 2013， 90（2）： 289-316.

［23］Sahoo D， Hoi S C H， Zhao Peilin. Cost sensitive online multiple kernel classification ［C］// Proc of the 8th Asian Conference on Machine Learning. Cambridge： JMLR， 2016： 65-80.

［24］Jain P， Kar P. Non-convex optimization for machine learning ［J］. Foundations and Trends in Machine Learning， 2017， 10（3）： 142-336.

［25］Wang Zhuang， Crammer K， Vucetic S. Breaking the curse of kerneli-zation： budgeted stochastic gradient descent for large-scale SVM trai-ning ［J］. Journal of Machine Learning Research， 2012， 13： 3103-3131.

［26］Li Junlong， Li Peipei， Hu Xuegang， et al. Learning common and label-specific features for multi-Label classification with correlation information ［J］. Pattern Recognition， 2022， 121： 108259.

［27］Lyu Jiaqi， Wu Tianran， Peng Chenlun， et al. Compact learning for multi-label classification ［J］. Pattern Recognition， 2021， 113： 10783.