多維背包問題的新型人類學習優化算法

摘 要：

針對目前算法求解多維背包時精度低、穩定性差、特別是無法有效求解超大規模算例等問題，提出一種新型人類學習優化算法。首先，基于認知心理學中的記憶理論，在基本人類學習算法中采用哈希函數表示人類在學習過程中的記憶行為，避免重復搜索，提高算法搜索群體多樣性；其次，采用認知心理學中的對比認知理論對學習算子選擇策略進行自適應調整；最后，采用變鄰域搜索操作提升算法局部搜索能力。采用小規模、中等規模、大規模、超大規模共76個多維背包問題的標準測試數據集進行數值實驗，并將新算法和二進制粒子群算法、遺傳算法、人類學習算法以及融合學習心理學的人類學習算法進行比較。結果表明新算法能夠有效求解四種規模算例。與其他算法相比，新算法具有更高的尋優精度和更好的穩定性。此外，對提出的三種優化策略進行分析，測試其對提高算法搜索性能的有效性。

關鍵詞：人類學習優化算法；認知心理學；哈希函數；學習算子選擇策略；多維背包問題

中圖分類號：TP301.6"" 文獻標志碼：A""" 文章編號：1001-3695（2024）12-022-3689-12

doi： 10.19734/j.issn.1001-3695.2024.04.0127

Novel human learning optimization algorithm for

multidimensional knapsack problem

Zhang Yipeng， Liu Yong， Ma Liang

（Management School， University of Shanghai for Science amp; Technology， Shanghai 200093， China）

Abstract：

Aiming at the problems of low accuracy and poor stability of the current algorithms in solving multi-dimensional knapsacks， especially the inability to effectively solve super-large-scale arithmetic cases， this paper proposed a new type of human learning optimization algorithm. Firstly， the noval human learning algorithm used a hash function based on the memory theory in cognitive psychology to represent the memory behaviour of human beings in the learning process， avoiding repeated searches and improving the algorithm’s search group diversity. Secondly， the algorithm used the contrastive cognition theory from cognitive psychology to adaptively adjust the learning operator selection strategy. Finally， the algorithm used a variable neighborhood search operation to enhance the algorithm’s local search capability. This paper conducted numerical experiments using a standardized test dataset of a total of 76 multidimensional knapsack problems that covered small， medium， large， and very large scales. Experiments compared the new algorithm with binary particle swarm algorithms， genetic algorithms， human learning algorithms， and human learning algorithms that incorporated the psychology of learning. The results show that the new algorithm is able to solve the four scale instances efficiently. Compared with other algorithms， the new algorithm has higher accuracy in finding the optimum and better stability. In addition， this paper analyzed three proposed optimization strategies to test their effectiveness in improving the algorithm’s search performance.

Key words：human learning optimization algorithm; cognitive psychology; hash function; learning operator selection strategy; multidimensional knapsack problem

0 引言

多維背包問題（multidimensional knapsack problem，MKP）是一類經典的非確定性多項式（nondeterministic polynomial， NP）問題。自1955年Lorie等人［1］首次提出MKP模型以來，該模型在資本預算與項目選擇［1，2］、切割庫存［3］、集裝箱裝載［1］、分布式計算中資源的分配［5］和約束批準投票［6］等問題上有著廣泛的應用。作為經典0-1背包問題的變體，多維背包問題有著更嚴格的約束條件，模型更加復雜且求解難度更高［7］。在目前的研究中，MKP所應用于的現實問題規模逐漸增大，問題的計算量呈指數級增長，計算復雜度也隨之增加。模型維度高、約束強的特點與實際問題規模的擴大使得MKP問題存在較大的求解難度。目前對多維背包問題的求解方法可以分為精確算法與智能優化算法。在對精確算法的研究中，文獻［8］首次將分支定界算法引入MKP問題；文獻［9］對分支定界算法改進并應用于更大規模MKP問題中；文獻［10］首次將動態規劃算法應用于MKP問題，通過構造子狀態、遞推關系式對問題進行求解，精確算法雖能求得MKP問題的最優解，但無法應用于大規模問題。智能優化算法旨在找到問題的滿意解，目前求解MKP問題效果較好的有蟻群算法［11］、二進制粒子群算法［12］、遺傳算法［13］等。與精確算法相比，雖然智能優化算法能求解更大規模問題，但對于如規模大于100、維度超過10的問題應用較少，求解精度與穩定性仍需提高。綜上所述，由于MKP問題嚴格的多維約束條件與現實規模問題的增大導致問題難以求解，目前仍需設計能有效求解MKP問題的算法。

人類學習算法（human learning optimization，HLO）由Wang等人［14］于2014年提出，通過模擬人類的學習過程對問題進行求解。算法通過設計學習算子、個體學習算子和社會學習算子三種學習算子不斷提高個體的學習能力進行迭代尋優。HLO由于其具有易于實現、尋優能力強的特點，已經成功用于調度問題［15］、選址問題［16］、供應鏈網絡設計［17］、自動文本摘要［18］、爐膛燃燒火焰的精確快速識別［19］等。這表明HLO有著良好的優化性能與潛力。目前對HLO求解MKP問題的研究處于起步階段。Wang等人［20］首次將HLO應用于MKP問題中，通過增加再學習算子對算例進行求解。文獻［21］結合學習心理學對算法進行改進，并與遺傳算法等方法在求解MKP問題上進行對比，結果表明改進算法具有更好的性能。但上述人類學習優化算法僅能對部分規模MKP算例有效求解，并且算法穩定性與精度仍有待提高。此外，算法所求解的MKP問題規模均不超過10個約束、100個物品；特別對于20個約束、200個物品以及50個約束、500個物品等超大規模算例無法求解。

因此，本文針對以上存在的問題，結合認知心理學提出一種新型人類學習算法（novel human learning optimization，NHLO）。在學習過程中人腦會對所學知識進行記憶，本文通過哈希表與哈希函數模擬了人類在學習過程中的記憶行為，減少重復搜索，提高搜索群體的多樣性。本文結合對比認知理論對算法中學習算子的選擇策略進行改進，使得算法擁有動態調整算子選擇的能力，提高算法的尋優效率。此外，將算法與變鄰域搜索操作相結合，增強算法跳出局部最優與尋優能力。最后將本文算法應用于四種不同規模的多維背包問題，驗證了所提出三種策略的有效性與新型算法的性能。

1 多維背包問題

多維背包問題的數學模型可定義為

max z=∑Mi=1cixi（1）

s.t. ∑Mi=1kijxi≤bj" "j=1，2，…，J（2）

xi∈{0，1}" i=1，2，…，M（3）

其中：J、M分別表示背包中的資源與物品數量；ci表示第i個物品的價值；kij表示第i個物品對資源j的消耗量；bj為該資源的總量；xi表示決策變量，xi=1表示選擇該物品放入背包，xi=0表示不選擇該物品放入背包。多維背包問題的目標則是在滿足約束情況下選擇若干物品，使得放入背包物品的總價值最大。

與0-1背包問題相比，模型的約束條件增加，求解難度更大，屬于NP-難問題［22］。

2 基本人類學習算法

基本人類學習算法HLO主要包括群體初始化、學習算子和知識庫更新三個部分。

2.1 群體初始化

人類學習優化算法通過二進制編碼對解進行表示，具體表示方式為

x={xij，i=1，2，…，N; j=1，2，…，M;xij∈{0，1}}（4）

其中：N表示群體規模；M表示解的維數；xij表示第i個個體的第j個分量。

2.2 學習算子

2.2.1 隨機學習算子

在初期學習過程中，存在隨機獲取知識的過階段，算法通過隨機學習算子模擬該學習過程，其數學表達式為

xij=0" 0≤randlt;0.51" else（5）

其中：rand表示一個［0，1］的隨機數。

2.2.2 個體學習算子

個體學習是學習過程中的普遍現象，其表現為個體根據自己以往經驗進行學習。算法通過個體學習算子對其進行模擬。人類學習優化算法通過創建如式（6）（7）所示的個體知識庫（individual knowledge database， IKD）來存儲每個個體的歷史最好經驗，并通過式（8）進行學習。

IKD=ikd1ikd2ikdiikdN 1≤i≤N（6）

ikdi=ikdi1ikdi2ikdipikdiL=iki11iki12…iki1j…iki1Miki21iki22…iki2j…iki2M ikip1ikip2…ikipj…ikipM ikiL1ikiL2…ikiLj…ikiLM 1≤p≤L

（7）

xij=ikdipj（8）

其中：ikdi表示第i個人的個體知識庫；ikdip表示該個體第p個個體最優解；ikipj表示該個體最優解的第j個分量；L表示個體知識庫規模。

2.2.3 社會學習算子

社會學習算子代表個體向種群中最優個體進行學習的過程。社會知識庫（social knowledge database， SKD）如式（9）所示。

SKD=skd1skd2skdqskdH=sk11sk12…sk1j…sk1Msk21sk22…sk2j…sk2M skq1skq2…skqj…skqM skH1skH2…skHj…skHM 1≤q≤H

（9）

其中：skdq表示整個種群中第q個最優的歷史最優解；skqj表示其第j個分量；H表示社會知識庫的規模。個體按照下式進行學習：

xij=skdqj" 1≤q≤H（10）

人類學習算法通過以上三種算子對解空間搜索并不斷產生新解。三種算法的選擇策略如下：

uij=rand（0，1） 0≤rand≤prikipjprlt;rand≤piskqjelse（11）

其中：pr表示進行隨機學習的概率；pi-pr為進行個體學習的概率；1-pi為進行社會學習的概率。

2.3 知識庫的更新

知識庫IKD、SKD的更新策略如下：當每一代新生成解的適應度值大于知識庫中對應的最差解的適應度值或者知識庫中解的數量小于對應知識庫的規模時，則將新生成的解添加到對應的知識庫中。

3 新型人類學習算法

基本人類學習算法存在著計算精度不高、算法穩定性較差、優化速度慢等問題。從人類學習的角度來分析，HLO算法對人類學習機制的描述較為簡單，忽略了在學習過程中心理因素會對學習效果產生的巨大影響。為提高算法中個體學習效果，本文結合認知心理學對基本人類學習算法進行了如下改進：受到文獻［15］的啟發，通過加入小組學習算子提高算法性能；學習中的記憶行為，通過哈希表與哈希函數對解進行記憶，避免了算法中解的重復搜索，提高種群多樣性；根據對比認知理論，在選擇學習算子時將個體進行比較，賦予算法動態選擇算子的能力；最后將算法與變鄰域搜索算法結合，增強算法局部開發能力。

3.1 小組學習算子

在學習過程中，小組學習是一種常見學習方式，通過將群體分組，實現組內各成員的小組學習。與個體學習類似，文獻［15］通過建立式（12）所示的小組知識庫（team knowledge database， TKD），進行小組最佳經驗的存儲，并通過式（13）進行學習。

TKD=tkd1tkd2tkdrtkdR=

tkd11tkd12…tkd1j…tkd1Mtkd21tkd22…tkd2j…tkd2M tkdr1tkdr2…tkdrj…tkdrM tkdR1tkdR2…tkdRj…tkdRM（12）

Xij=tkdrj" 1≤r≤R（13）

其中：R表示小組知識庫規模；tkdr表示該小組知識庫中的第r個解；tkdrj表示該解的第j個分量。

3.2 基于哈希函數的解的記憶機制

在人類學習算法中，通過對更新策略的分析可以發現，隨著算法的進行，優于知識庫中最差解的個體會不斷地加入其中，這導致IKD、TKD、SKD中個體會逐漸趨同，通過三個知識庫學習得到的種群多樣性也會受到影響，導致算法進行大量的重復搜索與過早收斂，陷入局部最優。在實際的學習過程中，大腦會對已經學習過的知識或者已經完成的目標通過神經元的電信號編碼成記憶。新型人類學習算法通過引入個體的記憶機制，在選中當前最優解的同時將該解記憶以限制該局部最優解再次被選中，從而增加種群多樣性，防止算法重復搜索。

在認知行為學中，記憶發揮著重要的作用。在認知心理學中，記憶被定義為人腦對輸入信息進行編碼、存儲與提取的過程。

本文通過哈希映射、哈希表賦值與訪問實現人腦對信息編碼、存儲與提取的模擬。

對于一個候選解M′∈Ω，可以通過哈希函數h單向映射為一個哈希值h（M′），即M′∈Ω→{0，1，2，…，l－1}。該哈希值h（M′）作為哈希表H的索引，可以將解的記憶情況存儲在哈希表H中，H［h（M′）］=1表示該解已經訪問過，處于記憶狀態，H［h（M′）］=0則表示該解未被訪問過，可當做當前最優解。

為減小發生哈希沖突的概率，本文引入了三個哈希函數hk（M）（k=1，2，3）與哈希表Hk（k=1，2，3），哈希函數如下：

hk（M）=（∑ni=1wk（i）×xi） mod l（14）

其中：wk（i）=wk（i－1）+βk+rand（βk/2），wk（0）=βk，βk（k=1，2，3）為不同的固定值；rand（βk/2）為屬于［0，βk/2］的隨機數；xi為二進制編碼解中的第i個元素；l為哈希表的長度。通過將三個哈希表中對應哈希值位置的元素賦值為1，完成對該解的記憶操作，過程如圖1所示。

3.3 結合對比認知理論的學習算子選擇策略

算子的選擇既要考慮隨機性，又要考慮合理性。因此，算法在選擇學習操作時加入了個體適應度值對各個知識庫平均適應度值的比較。對比認知理論認為，人在作出決策時往往會受到認知對比的影響，當個體選擇學習操作時也應通過比較選擇學習庫進行學習。當存在TKD或SKD的平均適應度值優于個體的適應度值時，說明對應的小組學習或社會學習操作效果較好，選擇對應的學習操作，若TKD與SKD的平均適應度值均優于個體適應度值，則選擇適應度值更優的學習算子，否則選擇隨機學習算子。

Xij=rand（0，1）" 0≤rand≤pr（t）

ikipj pr（t）lt;rand且fi（t）gt;tavg（t）且fi（t）gt;favg（t）

tkipj pr（t）lt;rand且tavg（t）gt;fi（t）且tavg（t）gt;favg（t）

skipj pr（t）lt;rand且favg（t）gt;fi（t）且favg（t）gt;tavg（t）（15）

其中：tavg（t）、favg（t）分別為TKD與SKD的平均適應度值；pr（t）為進行隨機學習的概率，具體表達式如下：

pr（t）=prmax－prmax－prminTt（16）

3.4 變鄰域搜索

為提高算法的局部開發能力，在對個體進行學習得到新個體后，對該個體進行變鄰域搜索。本文對多維背包問題設計了交換、反轉、刪除三種鄰域搜索算子，如圖2～4所示。

1）交換算子

為防止交換后解不發生變化，本文交換算子分別從選中與未選中放入背包的物品集合中選出物品進行交換，如圖2所示。

2）反轉算子

本文反轉算子如圖3所示。

3）刪除算子

隨機選擇一個物品進行刪除，在不違反約束的前提下，按照物品價值重量比排序放入若干剩余物品，如圖4所示。

3.5 算法流程

求解MKP問題的新型人類學習算法主要步驟如下：

a）初始化階段：生成初始群體，并計算每個個體的適應度。將個體知識庫IKD、小組知識庫TKD和社會知識庫SKD初始化，個體放入對應的知識庫中。

b）學習階段：根據對比認知理論，按照式（15）（16），將個體適應度值與各個知識庫平均適應度值進行比較，動態選擇學習算子。

c）變鄰域搜索階段：對生成的新個體進行變鄰域搜索，得到局部最優解。

d）記憶階段：通過哈希函數與哈希表判斷該局部最優解是否處于記憶狀態。若該解未被訪問過，則在哈希表中將該解記憶，否則重新進行鄰域搜索，直至找到未記憶解。

e）更新階段：計算新一代個體的適應度值，對IKD、TKD、SKD進行更新。

判斷迭代次數是否大于最大迭代次數，若大于則終止，輸出最優解。

4 實驗分析

4.1 實驗設置

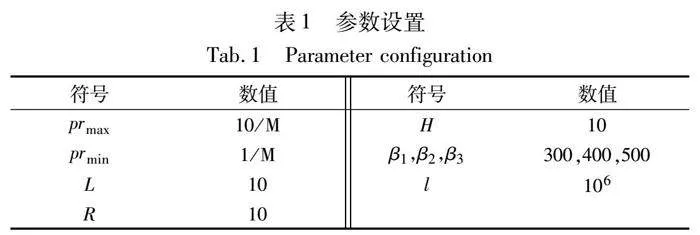
為驗證新算法性能，選取多約束背包問題MKP標準測試數據集進行數值實驗。如文獻［22］所示，本文數據集可從OR-Library（http：//people.brunel.ac.uk/～mastjjb/jeb/orlib/mknapinfo.html）獲取。將MKP問題的眾多數據集進行整理分類，將其分為由sento、hp、pb與weing 組成的小規模算例（set1）；由weish組成的中等規模算例（set2）；由chubeas中部分數據組成的大規模算例（set3）與由gk中部分數據組成的超大規模算例（set4）。此外，將所提算法與二進制粒子群算法（red-billed blue magpie optimizer，RBMO）［11］、遺傳算法（genetic algorithm，GA）［12］、簡單人類學習算法（simple human learning optimization，SHLO）［17］與融合心理學的人類學習算法（human learning optimization algorithm based on learning psychology，LPHLO）［21］進行比較。算法采用MATLAB R2022b編程實現，實驗環境為Intel Core i7-12700H和Windows 11操作系統。本文算法的參數設置如表1所示。

對于對比算法，均采用對應文獻的參數設置。各算法的最大迭代次數與種群規模均為1 000、100。

4.2 算法對比

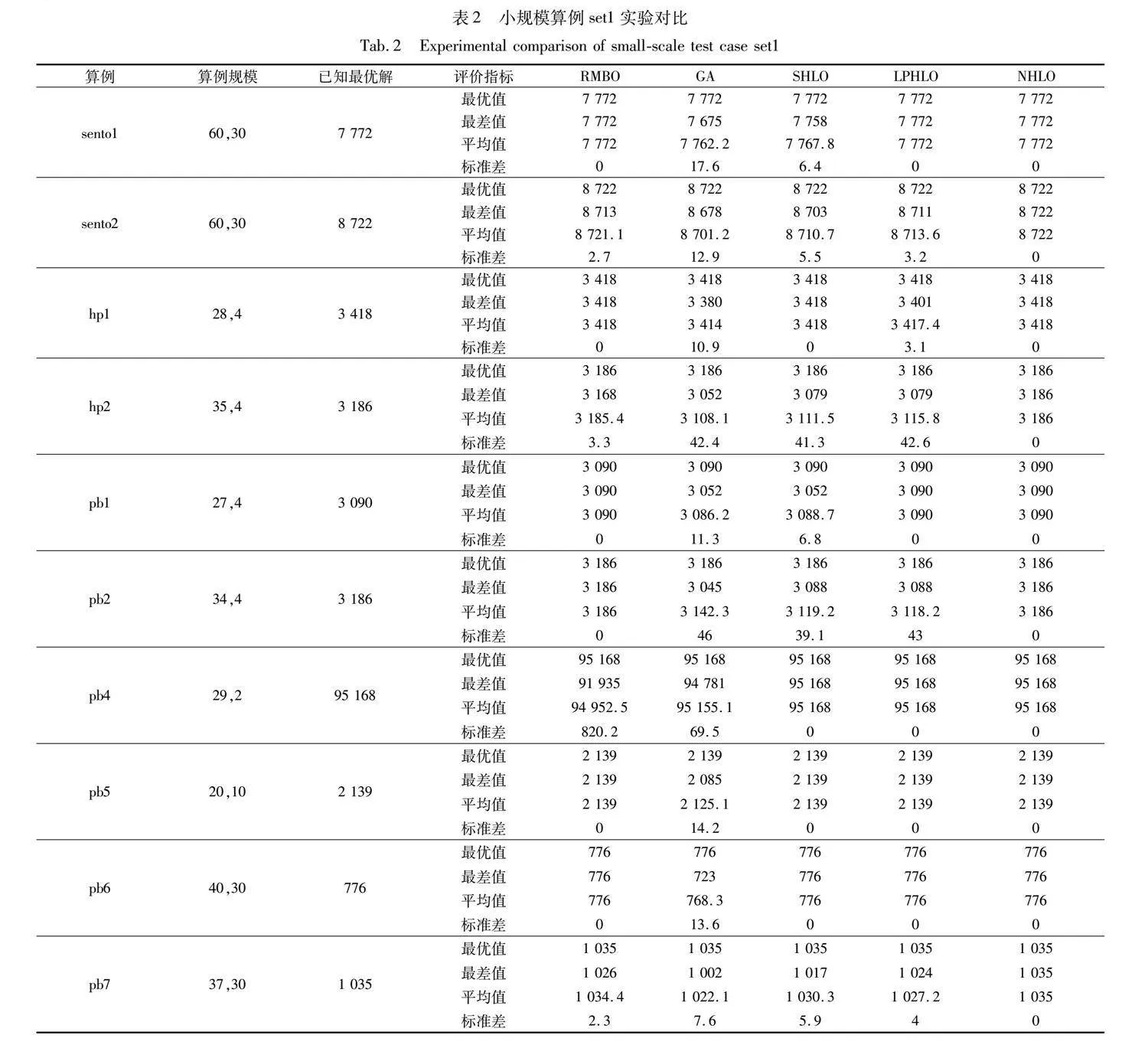
表2為RMBO、GA、SHLO、LPHLO和NHLO四種算法求解小規模算例set1的結果。結果表明NHLO、SHLO、LPHLO、RMBO與GA算法均能成功求出小規模18個算例的已知最優值。 NHLO的平均標準差為0，GA、RMBO、HLO與LPHLO算法18個算例的平均標準差分別為154.07、136.02、132.27、116.56。

上述實驗結果表明，在求解難度較低的小規模算例中，所有對比算法均能求得算例的已知最優解。但NHLO在求解小規模算例的穩定性明顯優于其余對比算法，每個算例30次實驗的已知最優解求得率均為100%。

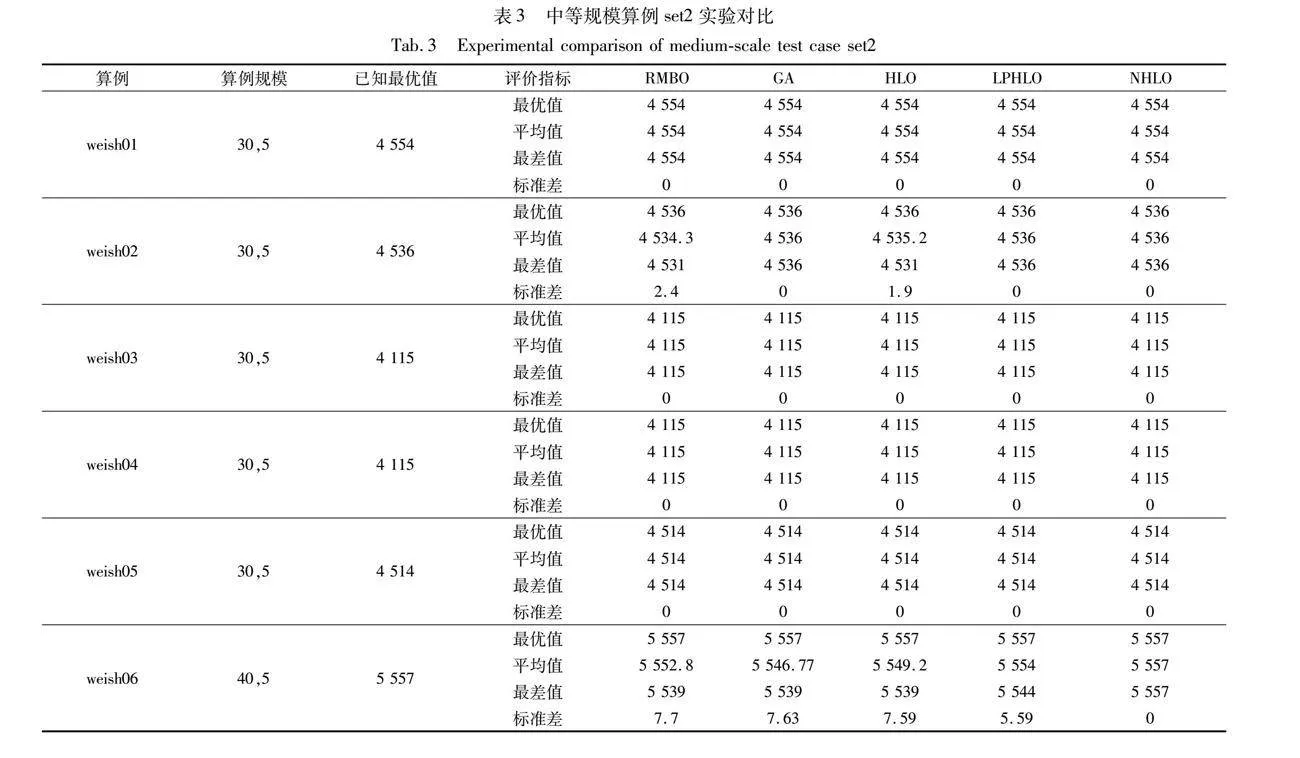
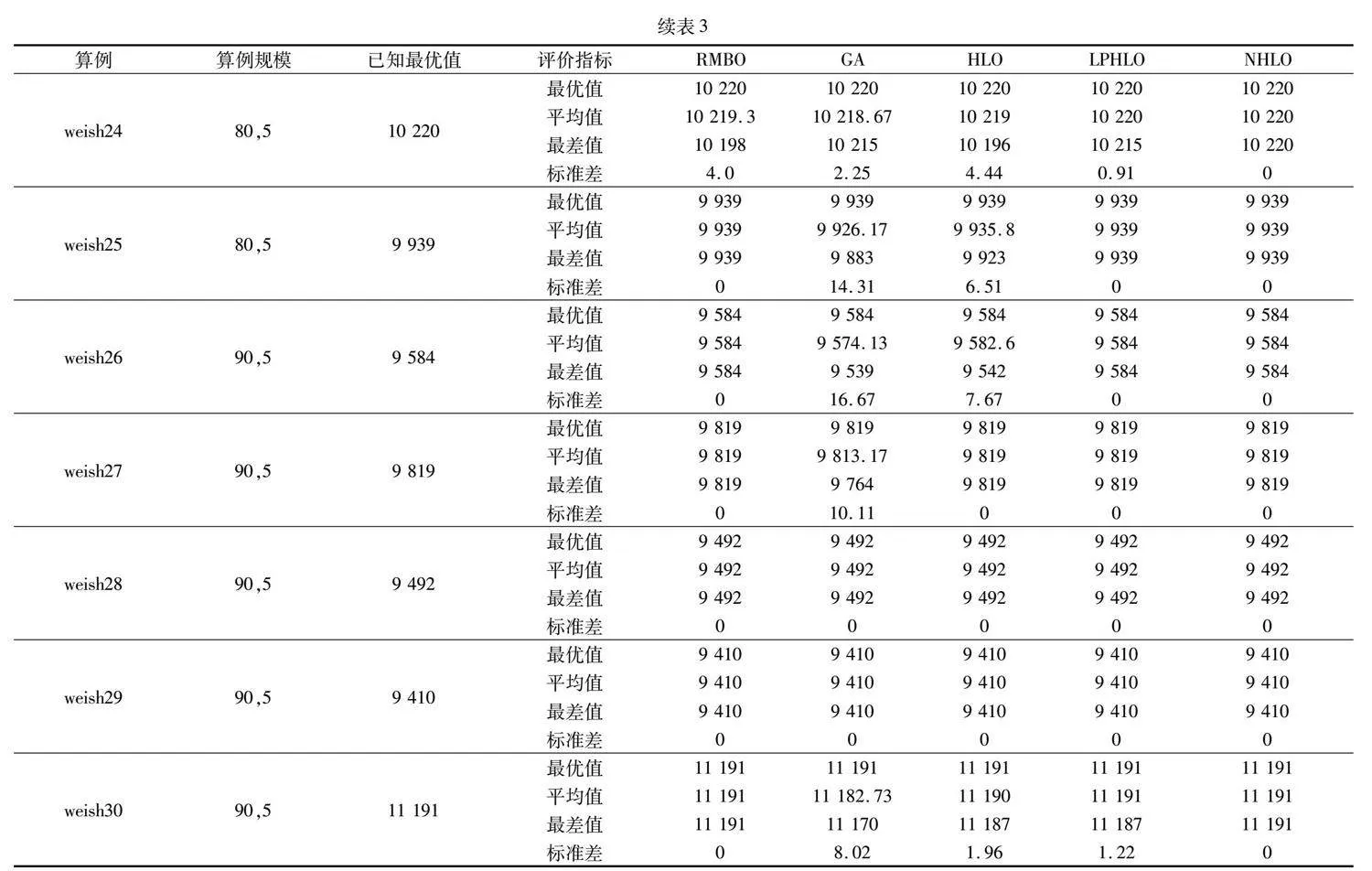
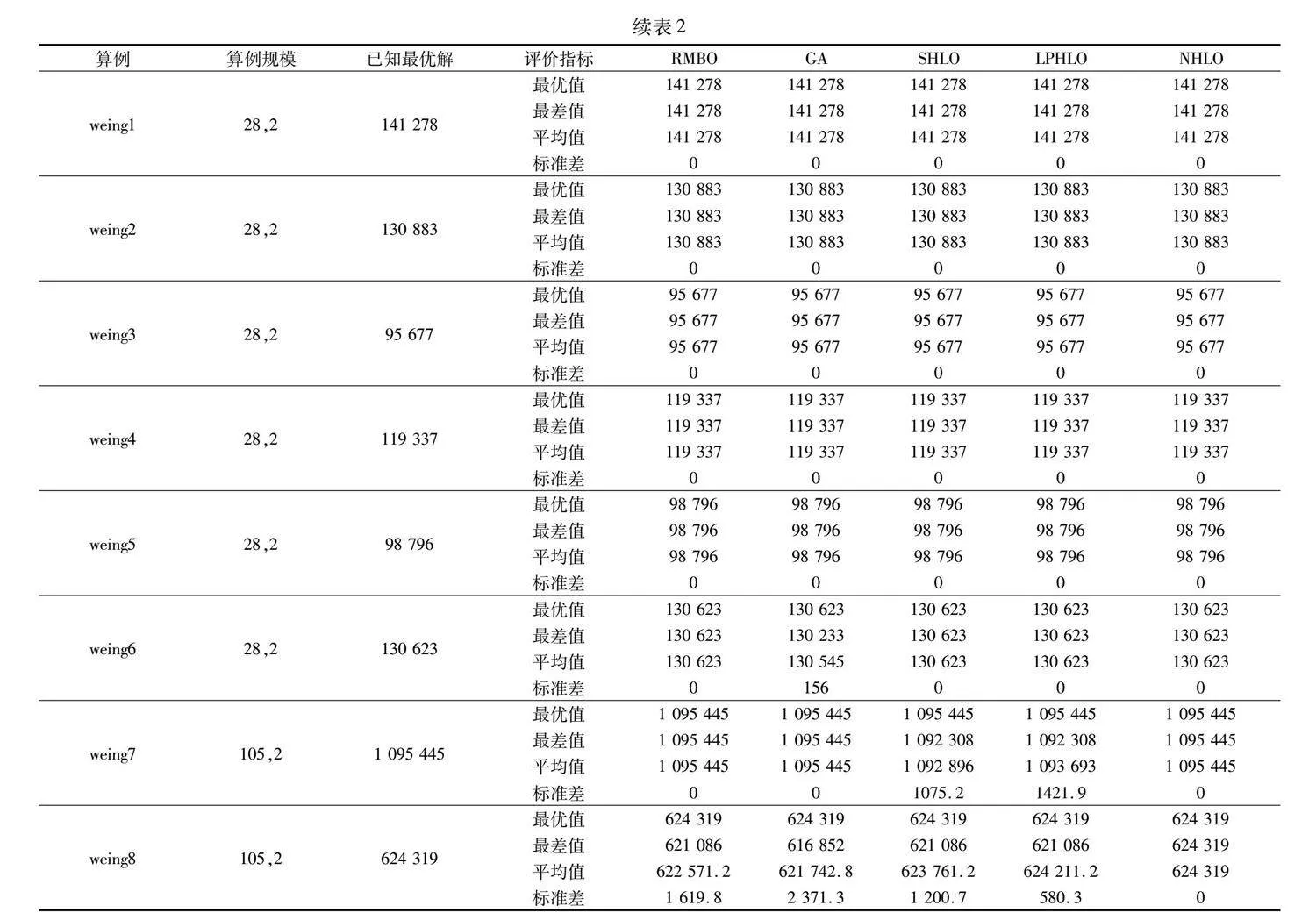
表3記錄了各個算法求解中等規模算例set2的結果。從結果可知，本文算法與RMBO能夠求解得到30個算例的最優解，但在求解的穩定性上本文算法明顯更優。雖然GA、SHLO與LPHLO能夠求出其中29個算例的最優值，但是NHLO平均值、最差值指標在29個算例中優于對比算法，所有標準差均為0。

以上實驗結果表明 NHLO算法在中規模算例上的求解精度、尋優能力與穩定性要明顯優于其余對比算法。

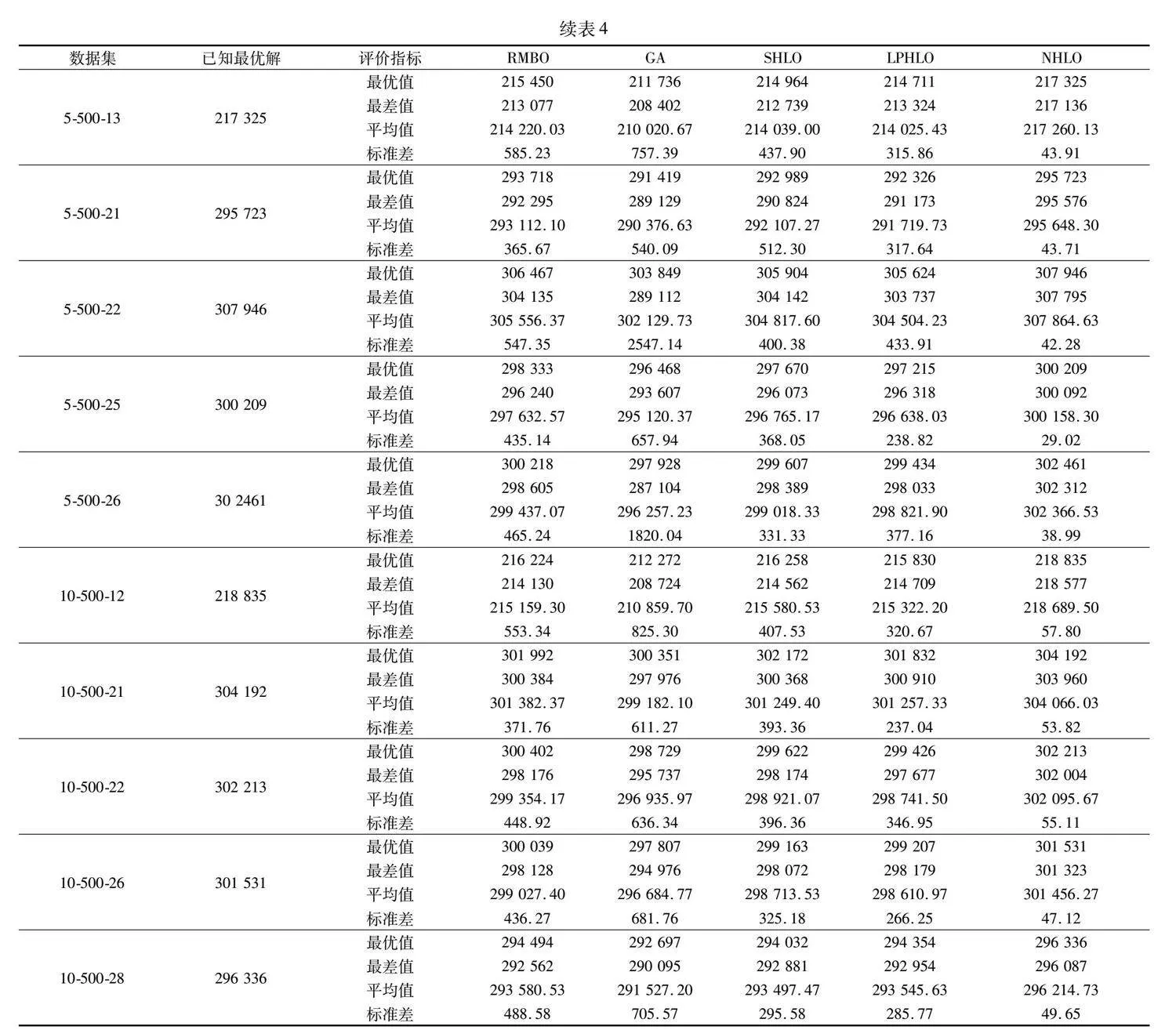
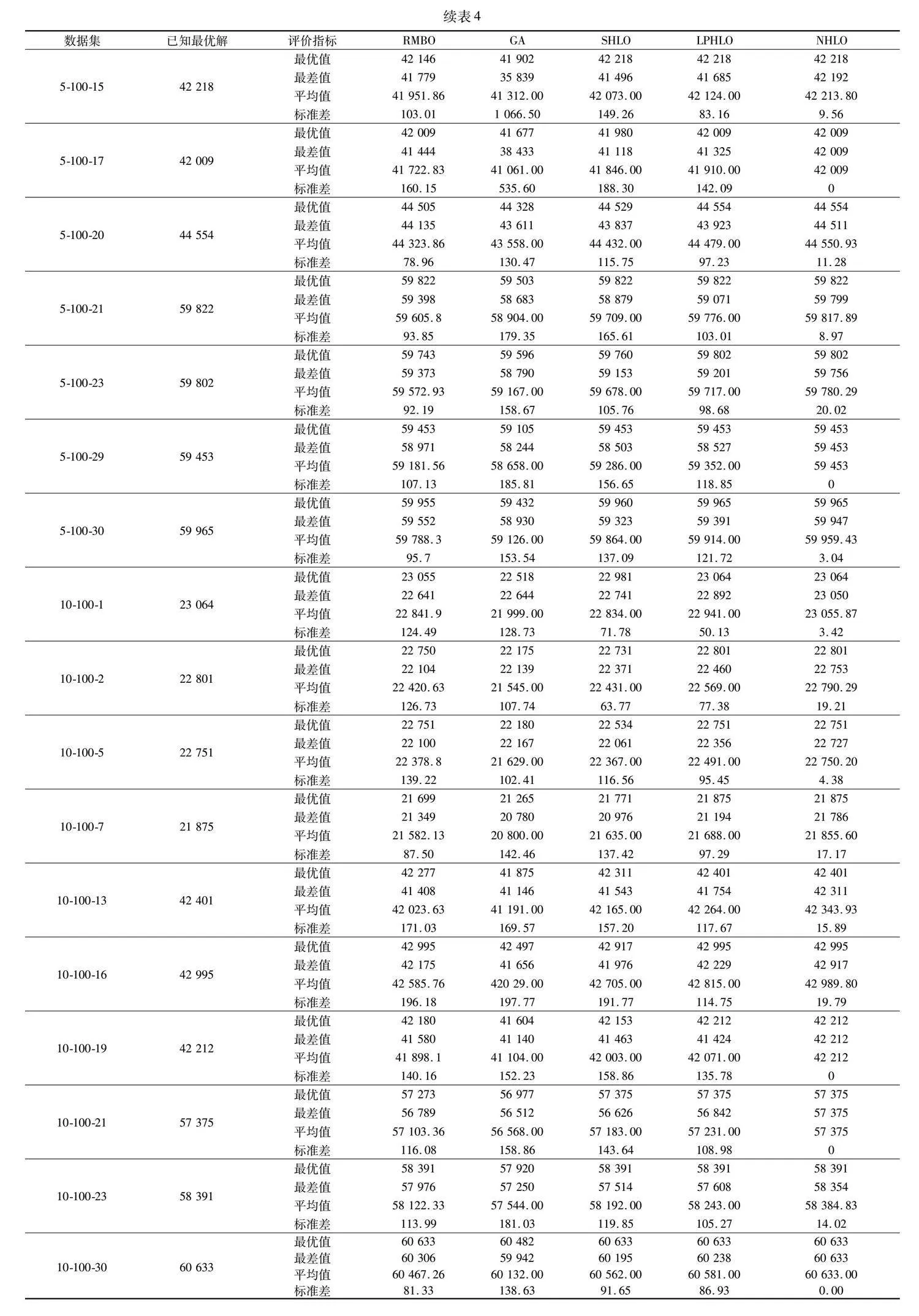
表4為NHLO與四種對比算法RMBO、GA、SHLO、LPHLO求解大規模算例set3的結果。其中，表格中的數據集列表示求解的數據集序號，5-100-1則表示規模為5個約束、100個物品的數據集中的第一個數據。從實驗結果來看，RMBO、GA、SHLO與LPHLO分別能夠求解出30個算例中6個、4個、7個、19個算例的已知最優解，NHLO能夠求得所有算例最優解。

通過表4可以發現，隨著算例規模的擴大，四種對比算法的求解能力有限，難以求得已知最優解。NHLO在大規模算例下求得的最優值與平均值更大、標準差更小。這表明算法對大規模問題的求解能力更強、求解穩定性更高。NHLO最差值大于對比算法，這表明算法通過對解進行記憶，有效地跳出了局部最優。

圖5為五種算法求解算例cb5-100-01、cb10-100-01、gk01、gk02的優化速度對比。由圖可知，NHLO求解以上四個算例的優化速度明顯優于其余對比算法。這是因為NHLO中解的記憶機制有效減少了解的重復搜索，提高了算法的優化速度。

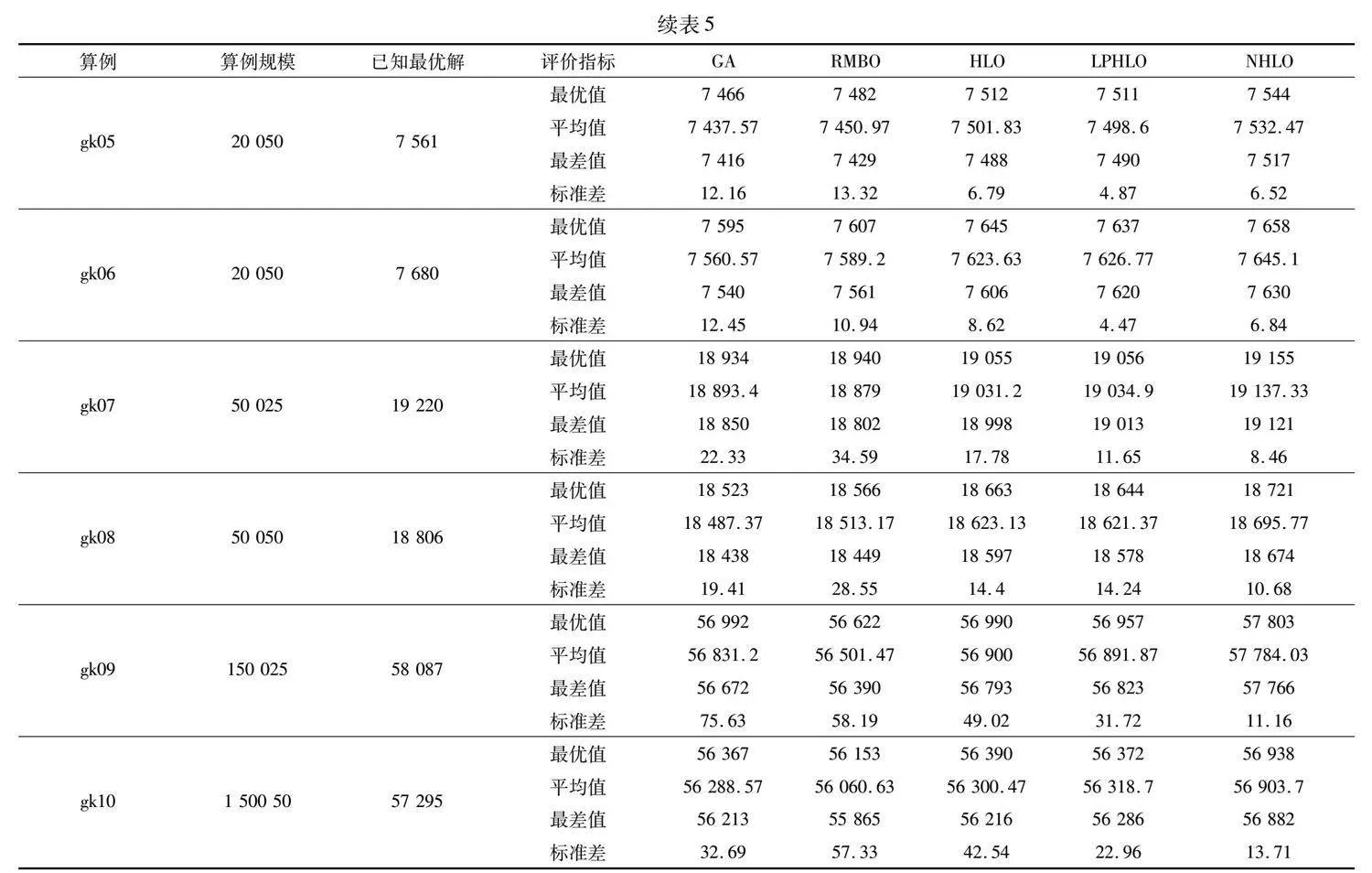
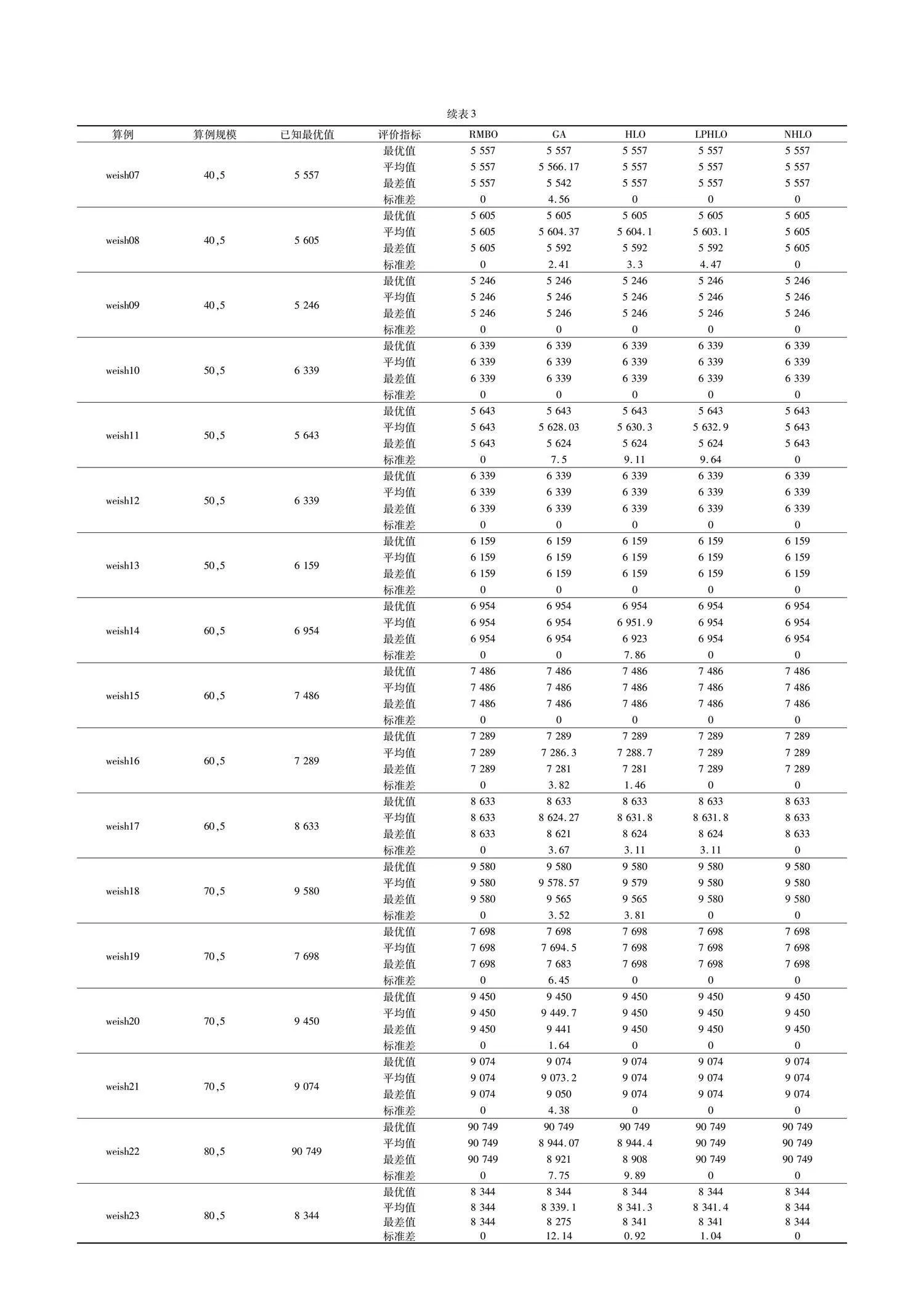
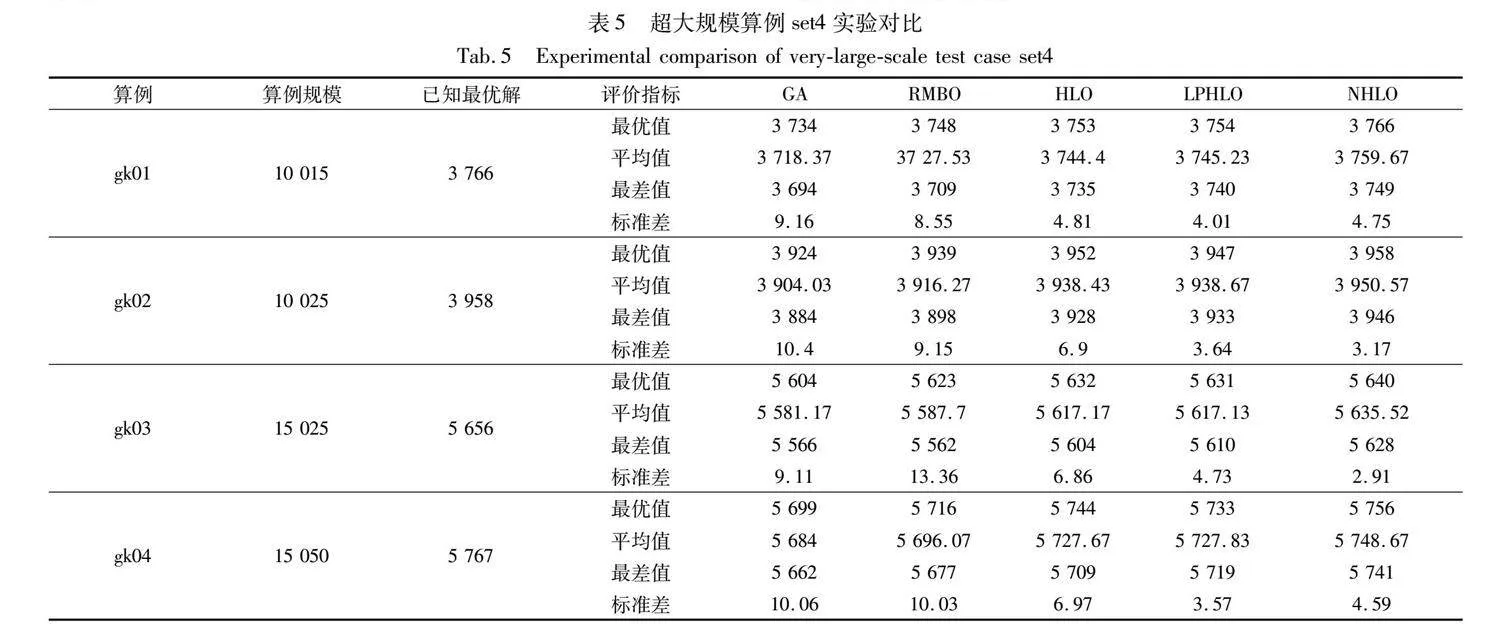
表5為五種算法求解超大規模算例set4的結果。可以發現在求解難度更高、數據規模超大的算例中，GA、RMBO、HLO與LPHO均無法求得已知最優解。NHLO能夠求得算例中4個算例的已知最優解，其余算例求得的最優值與已知最優解差距較小。

表5中LPHO求解gk01、gk04、gk05、gk06、gk11算例的標準差優于NHLO，但最優值與平均值低于NHLO。這表明LPHO雖求解結果穩定，但求解質量不高，易陷入局部最優。與對比算法相比，NHLO在求解更大規模的算例時，求解效果更好，性能優勢明顯。

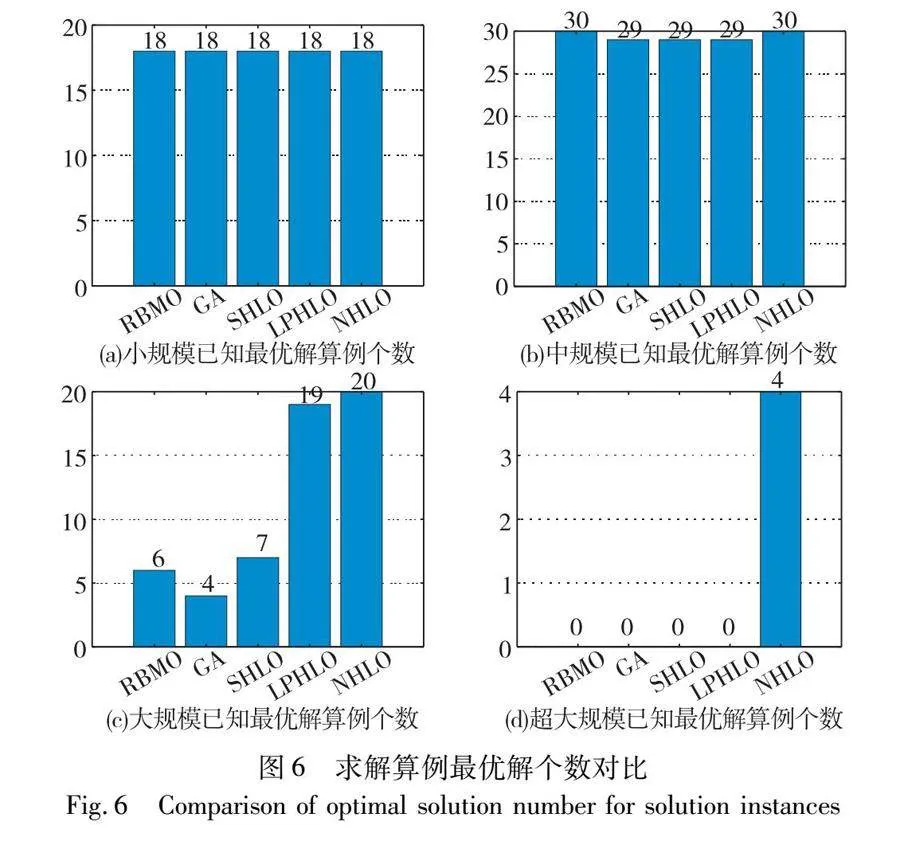
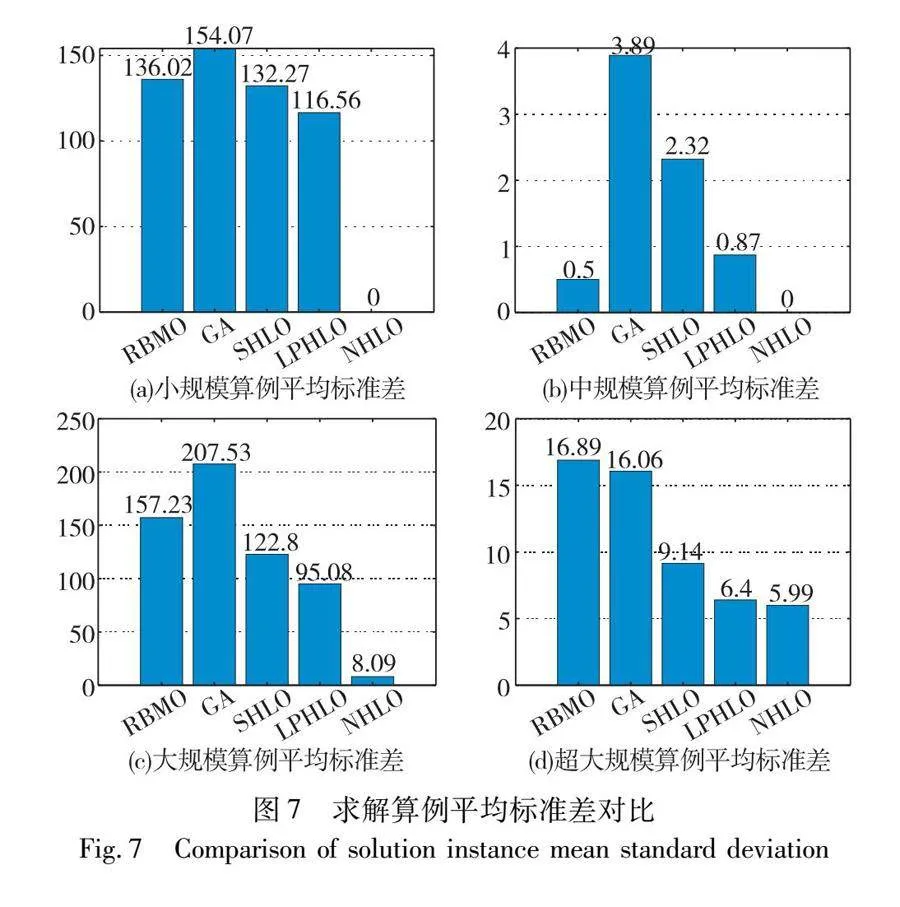
圖6、7分別給出了這五種算法求解算例最優解個數和平均標準差的比較情況。從圖5可知，NHLO在四種規模下成功求解算例個數高于四種對比算法，求解精度更高。圖6表明與其他算法相比，NHLO平均標準差更小，算法穩定性更高，且隨著算例規模的擴大，NHLO優勢更加明顯。

4.3 三種優化策略分析

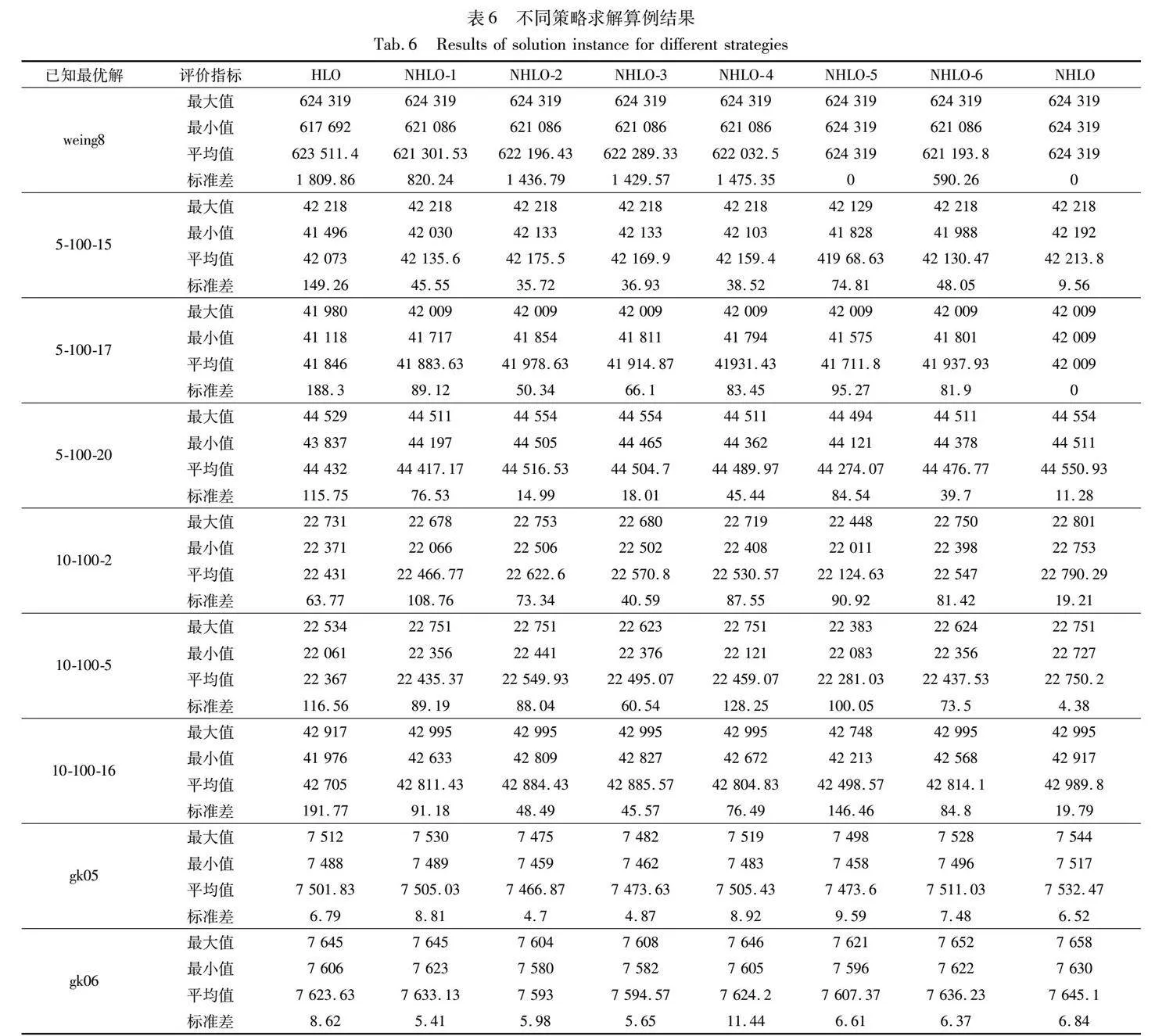
本文NHLO的主要優化策略包括基于哈希函數的解的記憶機制、結合對比認知理論的學習算子選擇策略和變鄰域搜索三種。為方便起見，分別用A、B、C表示這三種策略。為測試這三種優化策略的有效性，令NHLO1、NHLO2和NHLO3分別表示在基本HLO算法上增加A、B、C策略；NHLO4、NHLO5和NHLO6分別表示增加AB、AC、BC策略。求解不同規模算例的結果如表6所示。

通過表6可以發現：NHLO在四種評價指標的表現上明顯優于去除某一策略的算法NHLO-4、NHLO-5、NHLO-6。其中當本文算法去除B策略后（NHLO-5），與去除A策略（NHLO-6）和去除C策略（NHLO-4）相比，總體上最大值、最小值與平均值下降更為顯著，標準差增加更為顯著。這說明B策略（即對比學習算子選擇策略）對算法性能的影響大于A與C策略，為算法性能提升的主要來源。這是因為對比學習算子選擇策略能夠有效平衡全局探索與局部開發。算法通過對三種學習庫中解的質量進行比較，來動態選擇算子。當進行隨機學習時，算法進行全局探索；當進行個體、小組與社會學習時，算法進行局部開發。通過合理的算子選擇使得算法可行解質量更高、求得結果更加穩定。因此，NHLO-5與NHLO-4、NHLO-6相比，最大值、最小值與平均值更大，標準差更小。

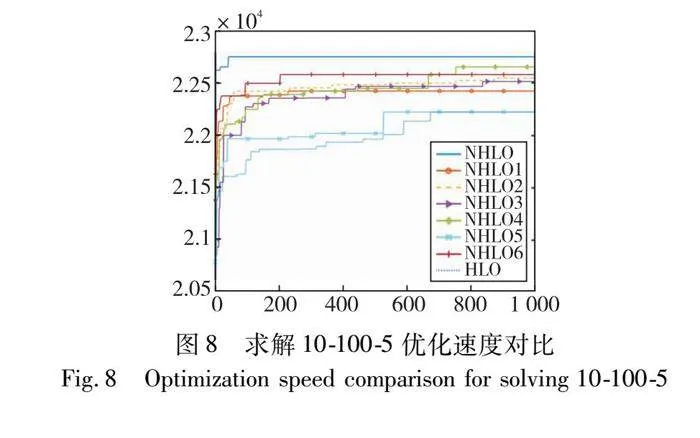
A策略為解的記憶機制，該策略通過對算法已經訪問過的解進行記憶，防止算法對解空間重復搜索，避免算法陷入局部最優。表6中，NHLO-1與基本HLO算法相比，NHLO-1求解最小值總體上大于HLO。這說明解的記憶機制能夠有效幫助算法跳出局部最優，導致最小值增大。C策略為變鄰域搜索操作，通過搜索鄰域中的解提高算法的局部開發能力。表6中加入C策略后，NHLO-3求得可行解的平均值總體上大于HLO算法。這表明算法通過對可行解進行鄰域搜索進一步提高了解的質量，使得總體的平均值提高。圖8為八個算法求解算例10-100-5的優化速度對比。結果表明A、B、C三種策略能夠有效提升算法的優化速度，且三種策略的融合能夠大幅提高算法求解MKP問題的優化速度。

綜上所述，解的記憶機制與變鄰域搜索能夠避免算法陷入局部最優并提高了局部開發的能力；對比學習算子選擇策略有效平衡了算法的探索與開發。實驗結果表明，三種策略均能有效增強算法的性能且三種策略的融合能夠大幅度提升算法的性能與優化速度。

5 結束語

本文針對現有算法求解MKP問題存在精度低、穩定性差、難以求解超大規模算例等問題，結合認知心理學提出了一種新型人類學習算法。本文設計了基于哈希函數的解的記憶機制、結合對比認知理論的學習算子選擇和變鄰域搜索三種策略來提升算法性能。本文將新型人類學習算法應用于小規模、中等規模、大規模、超大規模共76個MKP問題算例，并與GA、RMBO、HLO、LPHLO算法對比。實驗結果表明，本文算法在求解精度、求解穩定性以及優化速度方面明顯優于對比算法，能夠有效求解超大規模算例。為進一步驗證三種優化策略有效性，本文將三種策略排列組合加入HLO算法，求解不同規模算例。結果表明三種優化策略能夠有效提升算法的計算精度、穩定性與優化速度。后續可將算法應用于多目標背包問題。

參考文獻：

［1］Lorie J H， Savage L J. Three problems in rationing capital［J］. The Journal of Business， 1955， 28（4）： 229-239.

［2］Claude M， Donald R. Resource allocation via 0-1 programming［J］. Decision Sciences， 1973， 4（1）： 119-132.

［3］Gilmore P， Gomory R. The theory and computation of knapsack functions［J］. Operations Research， 1966， 14（6）： 1045-1074.

［4］Li Ying， Chen Mingzhou， Huo Jiazhen. A hybrid adaptive large neighborhood search algorithm for the large-scale heterogeneous container loading problem［J］. Expert Systems with Applications， 2022， 189： article ID 115909.

［5］Gavish B， Pirkul H. Allocation of databases and processors in a distributed data processing ［EB/OL］. （1982）. https：//api.semanticscholar.org/CorpusID：59647887.

［6］Straszak A， Libura M， Sikorski J， et al. Computer-assisted constrained approval voting［J］. Group Decision and Negotiation， 1993， 2： 375-85.

［7］王麗娜， 陸芷. 多維背包問題的啟發式算法研究探討 ［J］. 軟件， 2024， 45（2）： 34-36. （Wang Lina， Lu Zhi. Heuristic algorithms of multidimensional knapsack problem ［J］. Software， 2024， 45（2）： 34-36.）

［8］Wei S. A branch and bound method for the multi-constraint zero-one knapsack problem［J］. Journal of the Operational Research Society， 1979， 30（4）： 369-378.

［9］Fu Shengwei， Li Ke， Huang Haisong， et al. Red-billed blue magpie optimizer： a novel metaheuristic algorithm for 2D/3D UAV path planning and engineering design problems ［J］. Artificial Intelligence Review， 2024， 57（6）： 1-89.

［10］Thomas L， Augustine M. The imbedded state space approach to reducing dimensionality in dynamic programs of higher dimensions ［J］. Journal of Mathematical Analysis and Applications， 1974， 48（3）： 801-810.

［11］熊偉清， 魏平， 王小權. 蟻群算法求解多維0/1背包問題 ［J］. 計算機工程與科學， 2006， 28（10）： 78-79， 86. （Xiong Weiqing， Wei Ping， Wang Xiaoquan. Ant colony algorithm for solving multi-dimensional 0/1 knapsack problem ［J］. Computer Engineering and Science， 2006， 28（10）： 78-79， 86.）

［12］Aiman H E， Ahmad T S， Sadiq M S. Binary particle swarm optimization （BPSO） based state assignment for area minimization of sequential circuits ［J］. Applied Soft Computing Journal， 2013， 13（12）： 4832-4840.

［13］曾智， 楊小帆， 陳靜， 等. 求解多維0-1背包問題的一種改進的遺傳算法 ［J］. 計算機科學， 2006， 33（7）： 220-223. （Zeng Zhi， Yang Xiaofan， Chen Jing， et al. An improved genetic algorithm for solving multi-dimensional 0-1 knapsack problem［J］. Computer Science， 2006， 33（7）： 220-223.）

［14］Wang Ling， Ni Haoqi， Yang Ruixin， et al. A simple human learning optimization algorithm ［M］// Fei Minrui， Peng Chen， Su Zhou， et al. Computational Intelligence， Networked Systems and Their Applications. Berlin： Springer， 2014： 56-65.

［15］Ding Haojie， Gu Xingsheng. Hybrid of human learning optimization algorithm and particle swarm optimization algorithm with scheduling strategies for the flexible job-shop scheduling problem［J］. Neurocomputing， 2020， 414： 313-332.

［16］Shoja A， Molla-Alizadeh-Zavardehi S， Niroomand S. Hybrid adaptive simplified human learning optimization algorithms for supply chain network design problem with possibility of direct shipment［J］. Applied Soft Computing， 2020， 96： article ID 106594.

［17］Li Xiaoyu， Yao Jun， Wang Ling， et al. Application of human lear-ning optimization algorithm for production scheduling optimization［M］// Fei Minrui， Ma Shiwei， Li Xin， et al. Advanced Computational Methods in Life System Modeling and Simulation. Singapore： Springer， 2017： 242-252.

［18］Alguliyev R， Aliguliyev R， lsazade N. A sentence selection model and HLO algorithm for extractive text summarization［C］// Proc of the 10th International Conference on Application of Information and Communication Technologies. Piscataway， NJ： IEEE Press， 2016： 1-4.

［19］張平改， 費敏銳， 王靈， 等. 基于自適應顏色模型的爐膛火焰識別方法［J］. 中國科學： 信息科學， 2018， 48（7）： 856-870. （Zhang Pinggai， Fei Minrui， Wang Ling， et al. Furnace flame recognition method based on adaptive color model［J］. Science in China： Information Sciences， 2018， 48（7）： 856-870.）

［20］Wang Ling， Yang Ruixin， Ni Haoqi， et al. A human learning optimization algorithm and its application to multi-dimensional knapsack problems［J］. Applied Soft Computing， 2015， 34： 736-743.

［21］孟晗， 馬良， 劉勇. 融合學習心理學的人類學習優化算法［J］. 計算機應用， 2022， 42（5）： 1367-1374. （Meng Han， Ma Liang， Liu Yong. Human learning optimization algorithm integrating learning psychology［J］. Journal of Computer Applications， 2022， 42（5）： 1367-1374.）

［22］Chu P C， Beasley J E. A genetic algorithm for the multidimensional knapsack problem［J］. Journal of Heuristics， 1998， 4： 63-86.

［23］Cui Tianxiang， Du Nanjiang， Yang Xiaoying， et al. Multi-period portfolio optimization using a deep reinforcement learning hyper-heuristic approach［J］. Technological Forecasting and Social Change， 2024， 198： 122944.

［24］Han Yuhang， Zhang Miaohan， Nan Pan， et al. Two-stage heuristic algorithm for vehicle-drone collaborative delivery and pickup based on medical supplies resource allocation［J］. Journal of King Saud University-Computer and Information Sciences， 2023， 35（10）： 101811.

［25］Fréville A. The multidimensional 0-1 knapsack problem： an overview［J］. European Journal of Operational Research， 2004， 155（1）： 1-21.

［26］丁增良， 陳玨， 邱禧荷. 一種應用于旅行商問題的萊維飛行轉移規則蟻群優化算法［J］. 計算機應用研究， 2024， 41（5）： 1420-1427. （Ding Zengliang， Chen Jue， Qiu Xihe. Ant colony optimization algorithm based on Lévy flight transfer rule for solving traveling salesman problem［J］. Application Research of Computers， 2024， 41（5）： 1420-1427.）

［27］Kleinmuntz D N， Kleinmuntz C E. Multiobjective capital budgeting in not-for-profit hospitals and healthcare systems［D］. Champaign， IL： University of Illinois at Urbana-Champaign， 2001.

［28］Gearing C， Swart W， Var T. Determining the optimal investment poli-cy for the tourism sector of a developing country［J］. Management Science， 1973， 20： 487-497.