鄰域精英集體信息和種群全局信息自適應的多策略差分進化算法

摘 要：

為了使差分進化算法（differential evolution，DE）能夠更好地利用個體鄰域和整個種群的信息，提出了鄰域精英信息和種群全局信息自適應的多策略差分進化算法（adaptive multi-strategy differential evolution algorithm for neighborhood elite collective information and population global information，MSDE-NECPG）。首先，充分利用個體鄰域中多個精英個體的信息對變異策略進行引導，使搜索向更好的方向移動，提高開發能力。其次，為了讓鄰域的狀態能夠隨著搜索過程不斷地進化，引入鄰域更新機制。當鄰域最優個體連續多代更新失敗，鄰域可能陷入局部最優，此時擴大鄰域半徑，提高探索能力。同時，引入變異策略“DE/current-to-pbest”，這一策略不劃分鄰域，是基于種群的全局信息。兩個策略基于個體的改進率進行多策略的自適應，在局部信息和全局信息之間進行平衡。此外，為了防止參數的錯誤交互，縮放因子F、交叉率CR根據成功歷史積累進行更新，采用分組的參數自適應機制，不斷適應搜索過程。最后，為了驗證其有效性，在CEC2014的30個基準函數上，與 5 種迄今為止比較先進的差分進化算法進行比較，實驗結果表明，所提算法的精度、穩定性和收斂速度比得上這5種先進的算法。

關鍵詞：差分進化；鄰域精英信息；多策略自適應；參數自適應

中圖分類號：TP301.6"" 文獻標志碼：A""" 文章編號：1001-3695（2024）12-024-3710-06

doi： 10.19734/j.issn.1001-3695.2024.05.0118

Adaptive multi-strategy differential evolution algorithm for neighborhood elite collective information and population global information

Song Xiaoyu， Zhu Yanlin， Zhao Ming

（School of Computer Science amp; Engineering， Shenyang Jianzhu University， Shenyang 110168， China）

Abstract：

This paper proposed a multi-strategy differential evolution algorithm （MSDE-NECPG） to better utilize individual neighborhood and global population information in the differential evolution （DE） algorithm. Firstly， it fully utilized the information of multiple elite individuals in the individual neighborhood to guide the mutation strategy， moving the search towards better directions and enhancing the exploitation capability. Secondly， it introduced an update mechanism for the neighborhood to ensure its state evolved continuously throughout the search process. When the optimal individual in the neighborhood fails to update consecutively for multiple generations， the neighborhood may fall into a local optimum. At this point， this paper expanded the neighborhood radius to increase exploration capability. It introduced the mutation strategy “DE/current-to-pbest”， which was based on the global information of the population. These two strategies adaptively adjusted based on the improvement rate of individuals， balancing between local and global information. Furthermore， to prevent parameter error interaction， the scaling factor F and crossover rate CR were updated based on successful historical accumulations， employing a grouped parameter adaptive mechanism to continuously adapt to the search process. Finally， to validate its effectiveness， experiments were conducted on 30 benchmark functions from CEC2014， comparing it with five state-of-the-art differential evolution algorithms. The experimental results demonstrate that the proposed algorithm is comparable to these five advanced algorithms in terms of accuracy， stability and convergence speed.

Key words：differential evolution; neighborhood elite information; multi-strategy adaptive; parameter adaptive

0 引言

因為差分進化算法（DE）具有原理簡單、易于實現和魯棒性強等特點［1］，所以被廣泛應用于多個領域，比如動態經濟調度［2］、電力調度［3］和車輛路徑優化問題［4］等。然而，DE算法在面對復雜的問題時，容易出現過早收斂和陷入局部最優的問題，導致算法的停滯［1］。

為了充分利用種群個體周圍的信息，許多學者在變異策略中引入了鄰域。Tian等人［5］提出了基于鄰域的變異策略，利用鄰域中個體的適應度值來生成策略的選擇參數，并且根據鄰域的性能來識別鄰域的狀態，提出了鄰域的動態模型，緩解鄰域的進化困境。Yan等人［6］利用鄰域的歷史信息和種群的歷史信息生成變異策略，通過預測有希望的區域指導搜索，還引入了重啟機制，利用預測信息對較差的個體進行替換。這些基于鄰域的變異策略還可以進一步考慮與基于整個種群的策略組合使用，自適應地選擇變異策略，進一步平衡探索與開發。

為了充分利用不同變異策略的搜索特點，許多學者采用自適應的多種變異策略來提升算法的搜索能力。Qin等人［7］提出了一種自適應的差分進化算法，將四種變異策略進行結合，引入學習周期的概念，記錄不同策略在前LP代中生成的實驗向量成功進入下一代的個數和沒有進入下一代的個數，根據前幾代生成的有希望的解來生成策略的選擇概率。Mallipeddi等人［9］利用集成的方法，將不同的變異策略和控制參數集成到DE中，為變異策略生成一個變異策略池，每個控制參數都有一個值池，根據它們在過去幾代的成功率來選擇變異策略和控制參數。Wang等人［10］將三個變異策略和三種固定的參數組合分別放入策略池和控制參數池，三個策略每次從控制參數池中隨機選擇一種參數組合，生成三個實驗向量，從中選擇效果最優的組合。在變異策略的選取上需要考慮變異策略之間的能力搭配使得它們優勢互補，再結合自適應選擇策略才能充分發揮各自的作用。

許多學者還通過參數自適應的方式將控制參數自動更新到合適的值以使其適應算法的搜索過程。Zhang等人［8］利用歷史種群信息對控制參數進行自適應更新，使F服從柯西分布，Cr服從正態分布，記錄每一代的成功值，根據成功值對參數進行更新。Tanabe等人［11］采用加權算術平均值對μF和μCR進行更新，并且當下一代中存在更好的個體時，F由上一代成功F的加權算術平均值更新，Cr由上一代成功Cr的加權算術平均值更新。當代中沒有更好的個體產生時，F和Cr值保持與上一代相同。Meng等人［12］采用隨機普遍選擇將種群分為K組，對控制參數進行分組處理，每組F服從柯西分布，Cr服從正態分布，并且引入了某個個體被分類到第k組的概率，根據概率對μCR獨立更新，防止了參數的錯誤交互。在參數自適應的選取上還應該進一步考慮參數自適應機制與策略的適配性和參數之間的相互影響。

基于上述相關研究的分析，在算法變異階段，可以考慮變異策略之間的搭配，形成基于個體鄰域的變異策略與整個種群的變異策略。采用多策略自適應機制，改善傳統差分進化算法在迭代過程中易陷入局部最優的問題。通過鄰域的動態更新，調整搜索能力，并且進一步設計參數自適應機制，考慮與策略的適配性和參數之間的相互影響，使參數更新符合進化需求，提高算法的效率。為此，本文提出了一種鄰域精英集體信息和種群全局信息自適應的多策略差分進化算法。

本文的主要貢獻如下：

a）將鄰域概念引入變異策略。為個體構建鄰域，在鄰域中隨機選取多個精英個體進行線性組合，利用精英個體的集體信息引導變異策略加大個體周圍的局部搜索能力。

b）對鄰域進行動態更新。當鄰域最優個體連續多代更新失敗時，擴大鄰域的范圍，避免搜索策略陷入局部最優，調整搜索能力。

c）個體鄰域和整個種群的變異策略進行多策略自適應選擇。在每一代基于個體的改進率自適應地選擇變異策略，適應進化需求。

d）設置參數自適應機制。參數按策略分組并自適應調整，對每一個變異策略分配一組參數，該組參數根據成功歷史積累進行自適應調整。并且，每組參數將F和CR分組進行更新，防止每一組參數之間的誤交互，更新到合適的值。

1 基礎DE算法

DE算法是一種用于全局優化的進化算法，其搜索過程分為以下幾個階段：

a）初始化階段：隨機生成一定數量的個體作為初始種群。第i個個體是xi， j={xi，1，xi，2…，xi，D}，其中D是維度。

xi， j=xlj+rand（0，1）（xuj－xlj）（1）

b）變異階段：變異操作是通過對這幾個不同個體的差異進行線性組合得到的。這個差異向量稱為變異向量。

vi=xr1+F（xr2－xr3）（2）

其中：F為縮放因子；xi表示種群中第i個個體。

c）交叉階段：將變異向量與目標個體進行交叉操作，生成一個新的個體。

ui， j=vi， j" if rand（0，1）≤CR or j=jrand

xi， j" otherwise （3）

d）選擇階段：比較新生成的個體與原始個體，選擇其中更優秀的個體作為下一代的種群。

xi=ui" if f（ui）≤f（xi）

xi" otherwise（4）

e）終止條件：當函數評估的次數達到函數評估的最大次數（FESmax）時，算法將停止運行，輸出數據。

2 改進算法

2.1 鄰域精英集體信息引導的變異策略（NECI）

變異策略在差分進化算法中具有重要的作用，現在的研究中，大多數的變異策略是基于整個種群的搜索。相比于整個種群的搜索，基于鄰域的變異策略更注重局部搜索，可以避免過度探索導致搜索空間過大、計算復雜度過高的問題。但不是鄰域中所有的個體都可以引導變異策略向好的方向發展，所以本文利用鄰域中精英個體進行引導，并且為了避免一個固定的精英個體可能產生陷入局部最優的問題，又選取多個精英個體進行線性組合，引導變異策略向好的方向發展，并且具有一定的隨機性，不至于陷入局部最優。

NECI變異策略采用基于索引的環型拓撲結構為每個個體創建鄰域N（i），鄰域的索引范圍以當前個體為中心上下各一半，引入鄰域精英集合信息的均值xcnbest，它是在鄰域中適應度值排名前20%的個體中隨機選取m個個體的集合，m是在［1，20%N（i）］中隨機生成的一個整數，保證在鄰域中選擇多個精英個體的同時又增加隨機性，使精英集合信息能夠引導變異策略向好的方向發展的同時又減少了陷入局部最優的可能。

本文提出的NECI變異策略如下：

v1i， j=xi， j+F（xcnbest， j－xi， j）+F（xnr1， j－xnr2， j）（5）

其中：F為縮放因子；nr1、nr2是來自個體xi的鄰域N（i）中的隨機整數，且nr1≠nr2≠i；xnr1的適應度值大于xnr2的適應度值。xcnbest， j計算公式如下：

xcnbest， j=∑mk=1wk*xk， j（6）

同時，為了保證精英集合信息能夠向好的精英個體偏向，往更好的方向引導變異策略，引入權重因子wk。通過權重因子決定個體的比重，使鄰域中越好的個體所占的比重越多，以此來引導策略找到更好的進化方向。wk的計算公式如下：

wk=m－k+11+2+…+m" k=1，2，…，m（7）

2.2 鄰域動態更新機制

鄰域半徑決定著鄰域的范圍大小，對算法的搜索能力、收斂速度有著密切的聯系。較小的鄰域半徑使得算法能夠快速地收斂到局部最優解的附近，提高算法的收斂速度，但是過小的半徑容易使算法陷入局部最優。較大的鄰域半徑會擴大搜索范圍，使得鄰域最優解接近全局最優解，但過大的鄰域半徑可能導致搜索空間過于龐大，增加計算成本并降低搜索效率。固定的鄰域半徑難以識別鄰域的進化狀態，當鄰域陷入局部最優或停滯時，會浪費大量的計算資源。為此本文引入鄰域動態更新機制，根據進化的狀態，及時調整鄰域的半徑，更新鄰域的范圍。

在這一機制中，引入鄰域最優個體xnbest，它是鄰域中適應度值排名第一的個體，代表著在當前的鄰域范圍內找到的具有最優性能的解。記錄xnbest連續多代更新失敗的次數，可以幫助識別鄰域的進化狀態，如果xnbest多次更新失敗，可能意味著算法已經陷入局部最優或停滯。

在開始時，將xnbest連續更新失敗的次數設置為0，當xnbest沒有更新時次數增加1，當獲得更好的xnbest時，次數回歸到0。當次數到達規定閾值時，表示鄰域最優個體連續多代更新失敗，此時鄰域可能陷入局部最優或停滯，可以通過增加鄰域半徑，擴大鄰域范圍，增加鄰域的多樣性。

Nri=Nri+10%NP

其中：Nri是N（i）的半徑，將Nri初始化為10%NP，以保證算法在早期階段的探索。

本文的鄰域動態更新機制利用鄰域的最優個體來識別當前鄰域的進化狀態，通過擴大鄰域半徑，向鄰域內增加新個體，提高其多樣性。這一方法能夠有效地利用鄰域個體信息，根據搜索過程中的情況自適應地調整鄰域大小，引導個體向更有希望的方向移動，提高鄰域的多樣性，幫助算法跳出局部最優。

2.3 多策略自適應選擇機制

為了平衡全局和局部的信息，本文引入了基于整個種群信息的變異策略DE/current-to-pbest，這一策略不劃分鄰域，使用整個種群中排名靠前的精英個體引導變異策略，擴大搜索范圍，提高算法的開發能力［8］。

變異策略DE/current-to-pbest的公式為

v2i， j=xi， j+F（xpbest， j－xi， j）+F（xr1， j－r2， j）（8）

其中：F為縮放因子；xpbest是當前種群中前p％個個體（p=0.05）；r1是［1，NP］中的隨機整數，r2是從P∪A中選取的，A是外部存檔，A初始化為空。將每代的劣解添加到存檔中。存檔大小超過固定閾值時，則從外部存檔A中隨機選擇解并刪除，r1≠r2≠i 。

由于這一策略更加側重于整個種群信息的使用，在多數情況下，可能會忽略搜索的精度。為此本文根據個體的改進率將基于整個種群信息的變異策略DE/current-to-pbest與基于個體鄰域信息的變異策略進行自適應策略選擇，保證搜索的廣度和精度。

在初始階段，每一個變異策略的機會均等，在每一代結束后，根據變異策略對個體的改進率更新策略選擇的概率參數，使算法自適應地選擇變異策略，識別個體狀態。策略選擇的概率參數設置為p1，將p1初始化為0.5，保證策略的機會均等，同時，為了保證在算法運行中每一個變異策略都可以被使用，改進率最小為0.2，最大到0.8，在0.2～0.8動態變化。

p1的更新公式如下：

pg+11=（1－c）pg1+cΔg1（9）

其中：c為學習率，為常數0.1；g為代數；Δg1是變異策略1的改進率，改進率的計算公式為

Δg1=min（0.8，max（0.2，w1w1+w2））（10）

其中：w1是變異策略1的新舊適應度差的和，w1的計算公式為

w1=∑ni=1f（xi）－f（ui）（11）

其中： f（a）表示個體a的適應度值。

改進率是在變異操作后個體在適應度上的改善程度，是評估個體變異后性能提升的一種指標［13］。本文提出的多策略自適應選擇機制根據變異策略對個體的改進率更新策略選擇的概率參數，能夠使算法根據進化的需求自適應的選擇變異策略，提高引導精準性，有效對變異策略進行引導。

同時本文選取的變異策略中用于引導的信息類別分別為基于鄰域精英集體信息和基于種群全局信息，其中基于鄰域精英集體信息更注重局部搜索，幫助算法更好地利用局部信息，可以避免過度探索導致搜索空間過大、計算復雜度過高的問題。而基于種群全局信息更加側重全局搜索，擴大搜索范圍，提高算法的開發能力。兩者搭配使用可以保證算法在進化過程中的精度與廣度，提高算法的效率［14］。

2.4 參數自適應機制

差分進化算法中控制參數縮放因子F和交叉率Cr對算法的性能和收斂速度有著重要的影響。為了更好地提高參數對變異策略的適應能力，為每個變異策略都設置一組參數池，這一參數池中有K組參數，根據成功歷史積累進行更新，以此來防止參數的錯誤交互，能夠很好地反映當前對參數大小的需求，同時通過分組可以使參數具有一定的隨機性，避免相同的參數失去參數的配合，提高多樣性。將整個種群分為k組，每組有唯一的一對μF-μCR，第 k組的位置參數μFk和交叉率μCRk使用公式獨立更新。

Δ fj=f（ugj）-f（xgj）

ws=Δ fj∑F∈SFK Δ fj

meanWL（SFK）=∑F∈SFKws*F2∑F∈SFKws*F

meanWL（SCRK）=∑F∈SCRK ws*CR2∑F∈SCRK ws*CR

μFK=meanWL（SFK）" if SFK≠

μFK otherwise

μCRK=meanWL（SCRK）" if SCRK≠

μCRK otherwise（12）

其中：SFK、SCRK表示第K組中生成比父代更好的實驗向量的個體的F和CR的集合。為了防止出現偏差，將μF、μCR收斂到一個極小值，本文采用加權的Lehmer均值對μF、μCR進行更新。根據如下公式分別生成第k組的縮放因子和交叉率。

FK=randc（μFK，σF）（13）

CRK=randn（μCRK，σCR）（14）

其中：μFk、μCRk初始化為0.5；為了保持F和CR值在小范圍內穩定波動，參考相關文獻參數自適應地設置［12］，將σF的初始值設定為0.2，σCR的初始值設定為0.1。如果生成了［0，1］之外的CRk值，則用最接近生成值的極限值（0或1）代替。當Fk gt; 1時，將Fk截斷為1，當Fk≤0時，再次生成有效值。

2.5 復雜性分析

復雜性是評估算法性能的重要標準，本節將分析MSDE-NECPG算法的復雜性，并與經典的DE算法進行對比分析。MSDE-NECPG算法與經典的DE算法的主要區別在于引入了NECI策略、鄰域動態更新機制、多策略自適應選擇機制和參數自適應機制。其中NECI策略的主要操作是對每個個體的鄰域進行排序并計算出鄰域精英集合信息的均值xcnbest，其復雜度分別是O（G·Nmax·log2N）和O（G·（NP·D+NP·20%Nmax·D+D）），其中G為最大迭代次數，Nmax表示最大的鄰域大小。鄰域動態更新機制在每一代判斷xnbest是否進行更新，其復雜度是O（G·NP·D）。多策略自適應選擇機制的主要操作是對每個個體進行排序并計算出變異策略的概率參數，其復雜度分別是O（G·NP·log2NP）和O（G·NP·D）。參數自適應機制主要操作是通過隨機普遍選擇進行種群分組，其復雜度是O（G·NP·k），k代表對種群劃分的組數，為常數4。因此MSDE-NECPG算法的復雜性為O（G·Nmax·log2N）+O（G·（NP·D+NP·20%Nmax·D+D））+O（G·NP·D）+O（G·NP·log2NP）+O（G·NP·D）+O（G·NP·k）=O（G·NP·20%Nmax·D），經典的DE算法的復雜度為O（G·NP·D）［6］。由于Nmax的大小往往比NP小很多，所以不會造成嚴重的額外計算負擔。

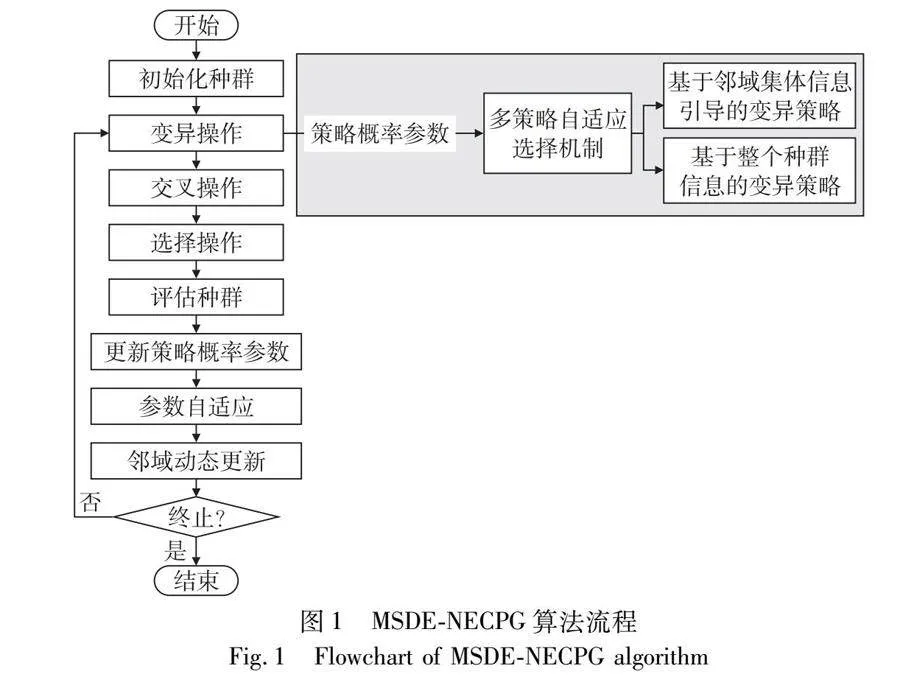
算法的流程如圖1所示。

3 實驗分析

在本章中，通過在CEC2014基準函數集上的30個基準函數進行實驗分析，評估了MSDE-NECPG算法的性能并與其他先進的算法進行了比較。CEC2014基準函數集被廣泛使用［15］，包含了多種不同類型的優化函數，如單峰函數、多峰函數、混合函數和組合函數。

3.1 實驗設計和參數設置

本文利用算法獨立運行51次記錄的平均值（mean error）和方差（std dev）衡量算法的精度、穩定性，并且利用收斂圖衡量算法的收斂速度。此外，采用Wilcoxon符號秩檢驗顯示兩個算法在0.05顯著性水平下的差異，采用Friedman檢驗顯示所有算法在測試集上的總體排名。

為了評價MSDE-NECPG的優勢，本文將MSDE-NECPG與五個改進的DE算法在D= 30、50和100時進行比較。這些算法包括JADE、EPSDE 、CIPDE、PALMDE和CoDE。其中JADE算法采用了變異策略DE/current-to-best進行更新，MSDE-NECPG算法雖然同樣使用了基于整個種群信息的變異策略DE/current-to-pbest，但與之不同的是，MSDE-NECPG算法將這一策略與鄰域精英集體信息引導的變異策略相結合，使變異策略基于種群全局信息和鄰域精英集體信息，可以保證算法在進化過程中的精度與廣度；CIPDE利用適應度值大于等于當前個體的集體信息引導的變異策略，MSDE-NECPG算法的NECI變異策略同樣使用了集體信息，但是與之不同的是，MSDE-NECPG算法利用的是鄰域中精英個體的集體信息，并且精英個體的選取是在排名前20%的個體中隨機選取，這樣在引導變異策略向好的方向發展的同時又增加了隨機性；EPSDE、CoDE和MSDE-NECPG均采用了多策略自適應機制，EPSDE根據在過去幾代的成功率來選擇變異策略，CoDE根據每一代不同策略生成實驗向量的效果來選擇效果最優的變異策略，MSDE-NECPG在每一代基于個體的改進率自適應地選擇變異策略，適應進化需求。PALMDE和MSDE-NECPG均對控制參數進行分組處理，其中PALMDE引入了某個個體被分類到第k組的概率，根據概率對μCR獨立更新，防止了參數的錯誤交互，MSDE-NECPG根據成功歷史積累進行參數的自適應調整。與這幾個算法比較可以更好地比較出MSDE-NECPG的精度、穩定性和收斂性。

實驗的參數設置如下，當函數評估的次數達到函數評估的最大次數（FESmax）時，算法將停止運行，將函數最大評估次數設置為10 000D，種群大小設置為10D，算法獨立運行51次。

本文對算法的核心參數進行了敏感性測試，分別對鄰域更新閾值和鄰域半徑更新大小進行了實驗。將動態鄰域更新閾值分別設置為50、70、90、100、110，鄰域大小的更新分別設置為1%NP、5%NP、10%NP、15%NP、20%NP，對其進行實驗驗證，比較不同參數設置下的均值和標準差。實驗結果表明上述參數存在敏感性，并且將動態鄰域更新閾值設置為100，鄰域大小的更新設置為10%NP時，算法的性能最好。本文篇幅有限，上述參數優化的實驗數據不進行展示。

3.2 比較與討論

3.2.1 均值和方差

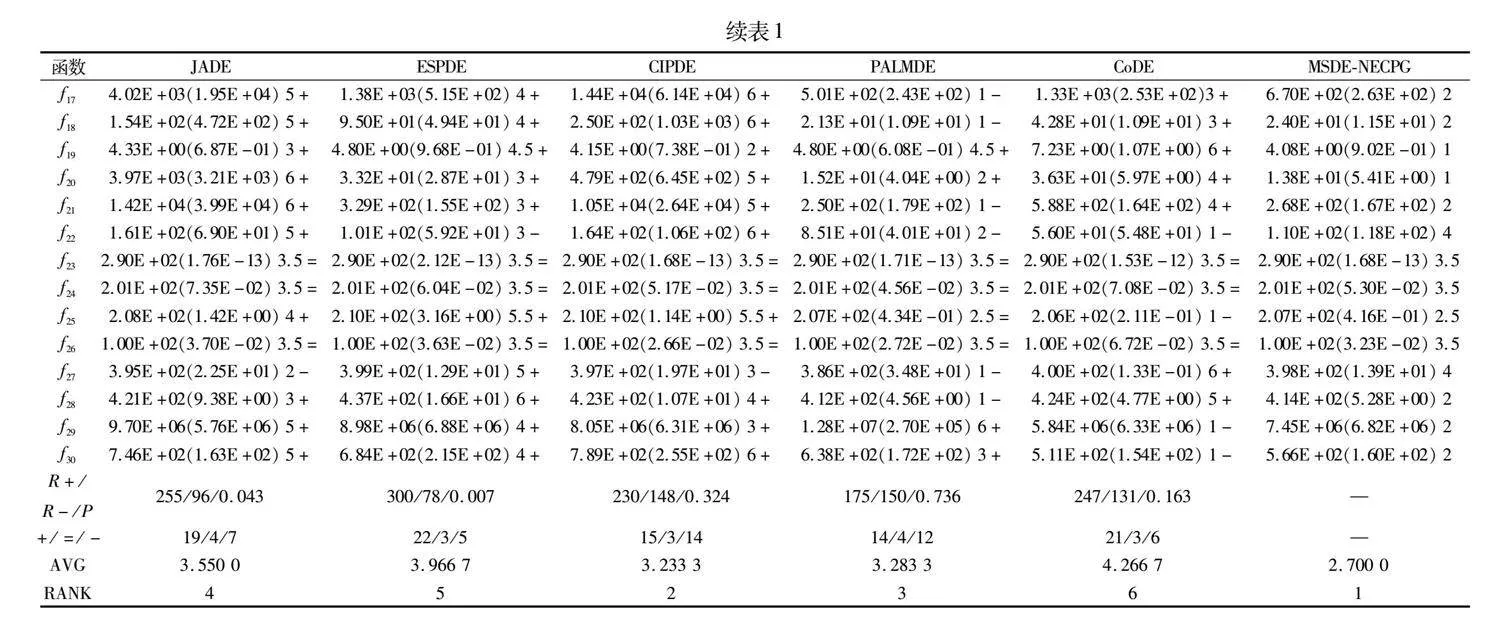
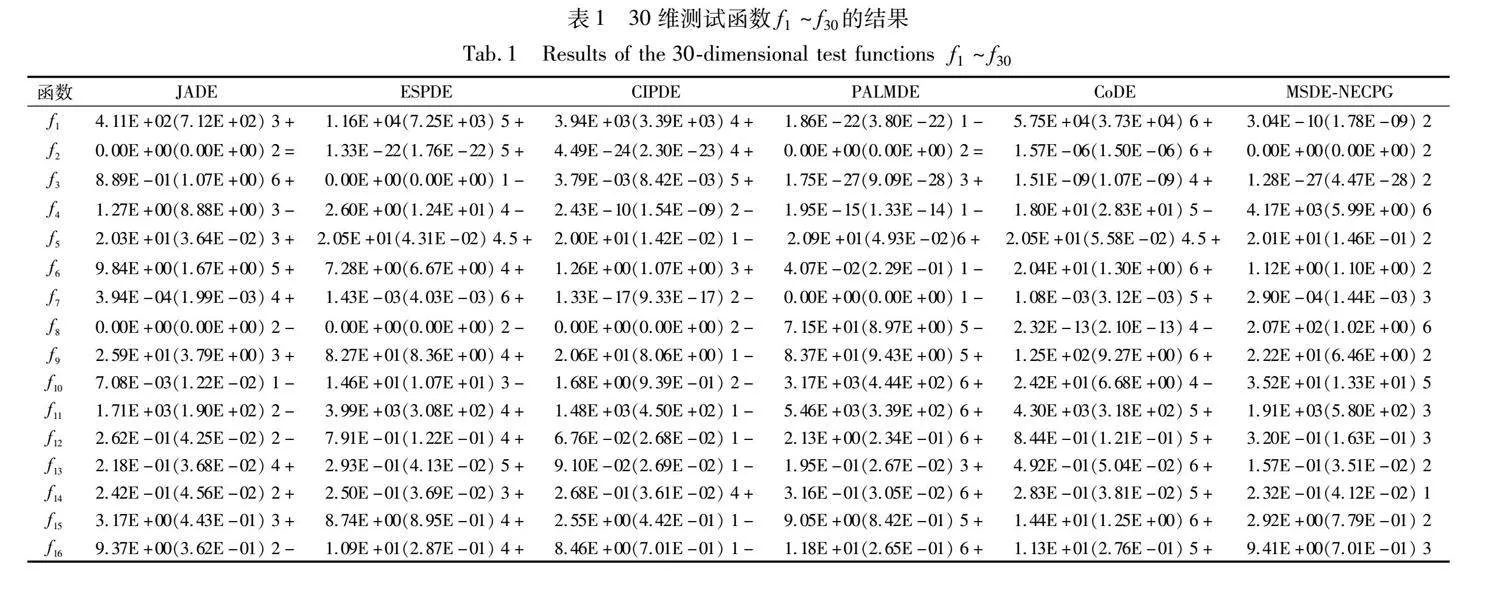
表1給出了算法在30維時，顯著性水平為0.05的Wilco-xon符號秩檢驗和Friedman檢驗的統計結果。“AVE”和“RANK”意指平均排名值和最終的排名。本文篇幅有限，50維和100維的實驗數據將不進行展示。

在30維時，MSDE-NECPG在第19、22、15、14、21個函數上的結果優于JADE、EPSDE、CIPDE、PALMDE、CODE。算法的平均排名分別為3.550 0、3.966 7、3.233 3、3.283 3、4.266 7、2.700 0，最終排名分別為4、5、2、3、6、1。

在50維時，MSDE-NECPG在第20、23、16、15、24個函數上的結果優于JADE、EPSDE、CIPDE、PALMDE、CODE。算法的平均排名分別為3.200 0、4.316 7、3.166 7、3.116 7、4.666 7、2.516 7，最終排名分別為4、5、3、2、6、1。

在100維時，MSDE-NECPG在第12、26、17、13、23、26個函數上的結果優于JADE、EPSDE、CIPDE、PALMDE、CODE。算法的平均排名分別為2.433 3、4.333 3、2.933 3、3.233 3、5.283 3、2.783 3，最終排名分別為1、5、3、4、6、2。

為了進一步研究算法的性能，本文在CEC2014 函數上進行Wilcoxon秩和檢驗，結果表明，在所有情況下，R+值均比R-值更高，在30維、50維、100維時，與JADE、EPSDE相比，P值小于0.05，存在明顯差異。在50維、100維時，與CoDE相比，P值小于0.05，存在明顯差異。

3.2.2 收斂圖

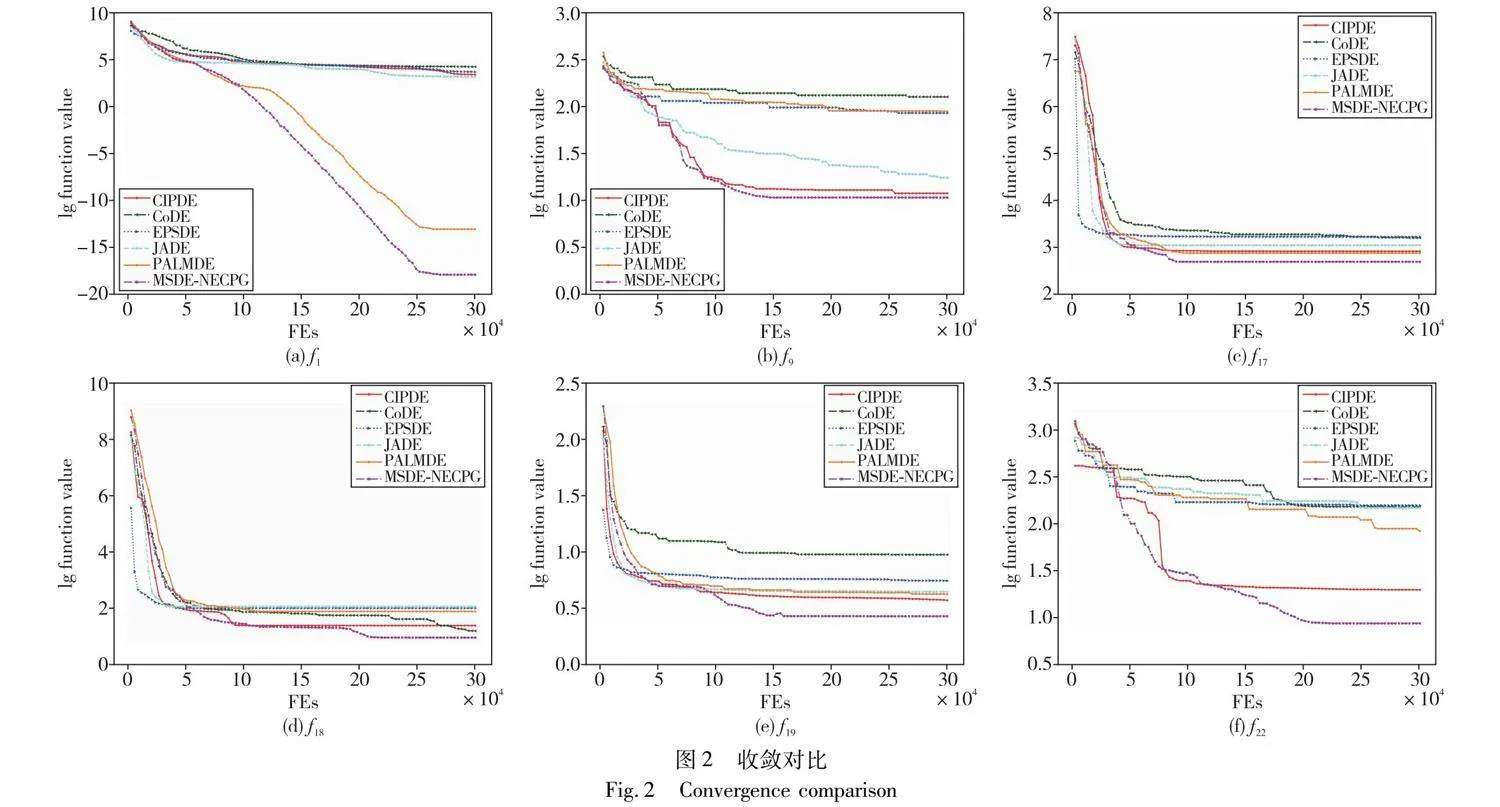
為了進一步展示其收斂性能，圖2給出了在CEC2014測試集30維上，MSDE-NECPG與上述DE變體在包括f1、 f9、 f17、 f18、 f19和f22在內的6個典型函數上的演化曲線（參見電子版）。這6個函數屬于不同類型的函數，其中f1屬于單峰函數， f9屬于多模函數， f17、 f18、 f19和f22屬于混合函數，選取幾個有代表性的函數可以反映不同類型函數的收斂性。

從圖2可以看出，在f1上，ESPDE 和 JADE 在前期收斂速度較快，但在進化中后期進入乏力階段，而 PALMDE 和 MSDE-NECPG 在中后期收斂速度較快，后期MSDE-NECPG 比 PALMDE 收斂更快，效率更高。在 f9上可以看到，ESPDE 和 MSDE-NECPG 在前期收斂速度較快，但ESPDE在進化中后期進入乏力階段，后期MSDE-NECPG收斂最快效率最高。在f17上ESPDE和 CoDE 在前期收斂速度較快，但在中后期進入乏力階段，而MSDE-NECPG 在進化后期收斂速度較快。在f18上ESPDE在前期收斂速度較快，但在中后期進入乏力階段，而MSDE-NECPG 在后期收斂速度較快。在 f19 中，可以看到MSDE-NECPG 在評估次數100 000次之后，與另外幾個算法的差距逐漸拉開，開始大幅收斂。 f22中，進化前期，大多數函數表現良好，但是在進化中期開始平穩，而 MSDE-NECPG中后期表現優異，收斂速度極快，達到了較好的收斂效果。

4 結束語

為了進一步挖掘個體鄰域的信息，增強算法的開發能力，本文將鄰域的概念引入變異策略，利用了精英集體信息對該個體的變異策略進行引導；為了讓鄰域的狀態能夠隨著搜索過程不斷地進化，結合搜索過程的需求，本文將鄰域進行動態更新，當鄰域最優個體連續多代更新失敗，擴大鄰域半徑，提高了探索能力。同時，引入基于整個種群信息的變異策略“DE/current-to-pbest”，基于個體的改進率進行多策略的自適應，更好地平衡了探索與開發。對于參數，根據成功歷史積累進行更新，采用分組的參數自適應機制，不斷適應搜索過程，防止了參數的錯誤交互。

在CEC2014的30個基準函數上的對比分析實驗結果表明，與五種先進的差分進化算法相比，所提算法的精度、穩定性和收斂速度比得上這五種先進的算法。

在后續研究中，尋找合適的方法將本文算法與ABC算法進行混合，進行算法的優勢互補，針對復雜程度不同的問題可以自適應地選擇算法，提高其效率。

參考文獻：

［1］丁青鋒， 尹曉宇. 差分進化算法綜述 ［J］. 智能系統學報， 2017， 12（4）： 431-442. （Ding Qingfeng， Yin Xiaoyu. Review of differential evolution algorithms ［J］. Journal of Intelligent Systems， 2017， 12（4）： 431-442.）

［2］肖鵬， 鄒德旋， 夏正龍，等. 改進差分進化算法在動態經濟調度中的應用 ［J］. 控制工程， 2021， 28（2）： 275-283. （Xiao Peng， Zou Dexuan， Xia Zhenglong et al. Improved differential evolution algorithm in the application of dynamic economic dispatch ［J］. Journal of Control Engineering， 2021， 28（2）： 275-283.）

［3］孫成富， 周海巖， 張亞紅. 基于差分進化算法的動態環境經濟電力系統調度優化 ［J］. 計算機科學， 2012， 39（11）： 208-211. （Sun Chengfu， Zhou Haiyan， Zhang Yahong. Dynamic environmental economic power system scheduling optimization based on differential evolution algorithm ［J］. Computer Science， 2012， 39（11）： 208-211.）

［4］宋強. 基于改進差分變鄰域算法的多行程車輛路徑問題的研究 ［J］. 重慶交通大學學報：自然科學版， 2020， 39（2）： 35-42. （Song Qiang. Research on multi-travel vehicle routing problem based on improved differential variable neighborhood algorithm ［J］. Journal of Chongqing Jiaotong University： Natural Science Edition， 2020， 39（2）： 35-42.）

［5］Tian Mengnan， Gao Xingbao. Differential evolution with neighborhood based adaptive evolution mechanism for numerical optimization［J］. Information Sciences，2019，478：422-448.

［6］Yan Xueqing， Tian Mengnan. Differential evolution with two-level adaptive mechanism for numerical optimization ［J］. Knowledge-Based Systems， 2022，241：108209.

［7］Qin A K， Huang V L， Suganthan P N. Differential evolution algorithm with strategy adaptation for global numerical optimization ［J］. IEEE Trans on Evolutionary Computation， 2009， 13（2）： 398-417.

［8］Zhang Jingqiao， Sanderson A C. JADE： adaptive differential evolution with optional external archive ［J］. IEEE Trans on Evolutio-nary Computation， 2009， 13（5）： 945-958.

［9］Mallipeddi， R， Suganthan P N， Pan Q K， et al. Differential evolution algorithm with ensemble of parameters and mutation strategies ［J］. Applied Soft Computing，2011，11（2）： 1679-1696.

［10］Wang Yong， Cai Zixing， Zhang Qingfu. Differential evolution with composite trial vector generation strategies and control parameters ［J］. IEEE Trans on Evolutionary Computation， 2011， 15（1）： 55-66.

［11］Tanabe R， Fukunaga A. Success-history based parameter adaptation for differential evolution ［C］// Proc of IEEE Congress on Evolutionary Computation. Piscataway， NJ： IEEE Press， 2013： 71-78.

［12］Meng Zhenyu， Pan J S， Kong Lingping. Parameters with adaptive learning mechanism （PALM） for the enhancement of differential evolution ［J］. Knowledge Based Systems， 2018， 141（1）： 92-112.

［13］Cui Laizhong， Li Genghui， Lin Qiuzhen， et al. A novel artificial bee colony algorithm with depth-first search framework and elite-guided search equation ［J］. Information Sciences，2016， 367： 1012-1044.

［14］Piotrowski A P. Adaptive memetic differential evolution with global and local neighborhood-based mutation operators ［J］. Information Sciences， 2013， 241（12）： 164-194.

［15］Tanabe R， Fukunaga A S. Improving the search performance of SHADE using linear population size reduction ［C］// Proc of IEEE Congress on Evolutionary Computation. Piscataway， NJ： IEEE Press， 2014： 1658-1665.