動態(tài)網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)及演化模式分析方法

摘 要：

如何充分考慮網(wǎng)絡(luò)的演化過程準(zhǔn)確發(fā)現(xiàn)動態(tài)網(wǎng)絡(luò)的社團(tuán)結(jié)構(gòu)，并對社團(tuán)演化模式進(jìn)行跟蹤和分析是動態(tài)網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)的重要挑戰(zhàn)。提出一種動態(tài)網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)及演化模式分析算法EC-DCD。該算法利用前一時刻的社團(tuán)發(fā)現(xiàn)結(jié)果作為先驗(yàn)信息來減少網(wǎng)絡(luò)噪聲對社團(tuán)發(fā)現(xiàn)的影響，利用演化聚類框架平滑連續(xù)時刻的社團(tuán)演化，獲得每個時刻準(zhǔn)確的社團(tuán)結(jié)構(gòu)。同時，引入社團(tuán)演化矩陣對社團(tuán)演化模式進(jìn)行建模和跟蹤，實(shí)現(xiàn)社團(tuán)演化模式的分析和可視化。實(shí)驗(yàn)部分，將EC-DCD同基線算法FacetNet、DYNMOGA、DNMF、NE2NMF和CoDeDANet在人工數(shù)據(jù)集與真實(shí)數(shù)據(jù)集上進(jìn)行了對比實(shí)驗(yàn)，實(shí)驗(yàn)結(jié)果證明EC-DCD不僅能夠準(zhǔn)確地劃分每個時刻的社團(tuán)結(jié)構(gòu)，具有較強(qiáng)的穩(wěn)定性，還能夠跟蹤社團(tuán)的演化模式。

關(guān)鍵詞：社團(tuán)發(fā)現(xiàn)；動態(tài)網(wǎng)絡(luò)；演化聚類框架；非負(fù)矩陣分解；演化模式

中圖分類號：TP181"" 文獻(xiàn)標(biāo)志碼：A""" 文章編號：1001-3695（2024）12-026-3722-07

doi： 10.19734/j.issn.1001-3695.2024.05.0141

Dynamic network community detection and evolution mode analysis method

Pan Yu1， Yao Feng1， Liu Xin2， Zhang Lei3， Wang Shuaihui4， Wang Pei1

（1.National University of Defense Technology， Changsha 410000， China; 2. Army Engineering University， Nanjing 310000， China; 3. Aca-demy of Military Science， Beijing 110000， China; 4. Naval Command College， Nanjing 310000， China）

Abstract：

How to obtain accurate community structure of the dynamic network， model the dynamic evolution process of the network， and realize the tracking and analysis of the community evolution mode is an important challenge for detecting dynamic network communities. This paper proposed a dynamic network community detection algorithm EC-DCD. The algorithm utilized the previous community detection results as a priori information to reduce the impact of network noise on community detection. It applied an evolutionary clustering framework to smooth the community evolution over consecutive time， achieving community structures at each time step. At the same time， it introduced the community evolution matrix to model and track the evolution mode of the community， which could realize the analysis and visualization of the community evolution mode. In the experiment， this paper tested the EC-DCD algorithm and baseline algorithms such as FacetNet， DYNMOGA， DNMF， NE2NMF， and CoDeDANet on the artificial datasets and the real datasets. The experimental results show that the proposed method EC-DCD can not only accurately detect the community structure at every moment， but also track the evolution pattern of the community.

Key words：community detection; dynamic network; evolutionary clustering; nonnegative matrix factorization; evolution mode

0 引言

在復(fù)雜網(wǎng)絡(luò)中，社團(tuán)結(jié)構(gòu)是廣泛存在的重要潛在結(jié)構(gòu)。發(fā)現(xiàn)網(wǎng)絡(luò)中的社團(tuán)結(jié)構(gòu)對探索網(wǎng)絡(luò)潛在特性、理解網(wǎng)絡(luò)組織結(jié)構(gòu)、發(fā)現(xiàn)網(wǎng)絡(luò)隱藏規(guī)律和交互模式等具有重要的理論和現(xiàn)實(shí)意義，是網(wǎng)絡(luò)分析任務(wù)的關(guān)鍵研究內(nèi)容［1］。在現(xiàn)實(shí)生活中，隨著網(wǎng)絡(luò)中節(jié)點(diǎn)和邊的增加與減少，網(wǎng)絡(luò)的拓?fù)浣Y(jié)構(gòu)和社團(tuán)結(jié)構(gòu)都會不斷發(fā)生演化。例如，在學(xué)術(shù)網(wǎng)絡(luò)中，擁有相同研究領(lǐng)域的學(xué)者往往構(gòu)成一個社團(tuán)，研究熱點(diǎn)的變化和研究者興趣的改變，使得社團(tuán)具有復(fù)雜的動態(tài)性。網(wǎng)絡(luò)的不斷演化可能導(dǎo)致社團(tuán)結(jié)構(gòu)的巨大變化和被重新發(fā)現(xiàn)的需求。通過挖掘動態(tài)變化的社團(tuán)結(jié)構(gòu)，人們能夠認(rèn)清網(wǎng)絡(luò)中隱含的內(nèi)部結(jié)構(gòu)，深入理解個體的行為特點(diǎn)和網(wǎng)絡(luò)演化趨勢，揭示網(wǎng)絡(luò)中存在的普遍性特征和規(guī)律。精準(zhǔn)挖掘動態(tài)網(wǎng)絡(luò)的社團(tuán)結(jié)構(gòu)不僅對揭示復(fù)雜網(wǎng)絡(luò)的結(jié)構(gòu)和網(wǎng)絡(luò)功能具有重要的理論意義，而且對于信息擴(kuò)散、輿情傳播、病毒感染等不同領(lǐng)域管理水平與治理能力的提高具有重要的現(xiàn)實(shí)指導(dǎo)意義。例如，在“新冠”病毒傳播引起的肺炎疫情中，病毒的傳播與感染者社交活動中存在的顯性或隱性社團(tuán)結(jié)構(gòu)密切相關(guān)，呈現(xiàn)聚集性特點(diǎn)。對其進(jìn)行社團(tuán)發(fā)現(xiàn)可以準(zhǔn)確識別和掌握病毒感染者的社團(tuán)歸屬特征，有助于快速鎖定密切接觸者，從而為疫情的防控起到積極的作用［2］。在云計(jì)算中，通過分析服務(wù)間的流量挖掘虛擬網(wǎng)元之間的社團(tuán)結(jié)構(gòu)，可以為數(shù)據(jù)中心的微服務(wù)部署和調(diào)度提供指導(dǎo)意見，進(jìn)一步優(yōu)化運(yùn)營商的效率并減少運(yùn)營代價；在IP網(wǎng)絡(luò)中，對IP網(wǎng)絡(luò)的社團(tuán)結(jié)構(gòu)進(jìn)行挖掘和分析有利于理解網(wǎng)絡(luò)流量，從而為網(wǎng)絡(luò)優(yōu)化和安全管理提供有用的信息和決策支持；在通話網(wǎng)絡(luò)中對用戶類別進(jìn)行識別有助于分析用戶通信模式和特征，從而提供定向的推薦服務(wù)和安全布控［3］。

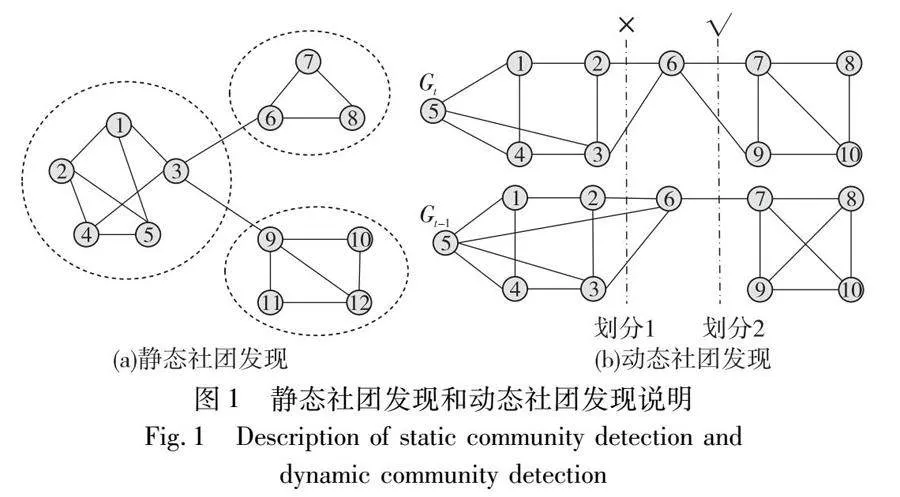
文獻(xiàn)［4］定義了社團(tuán)的新生、消亡、增長、收縮、持續(xù)、分裂和重生七種社團(tuán)演化行為。動態(tài)網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)不可預(yù)測和快速變化的特性為社團(tuán)發(fā)現(xiàn)提出了嚴(yán)峻的挑戰(zhàn)，傳統(tǒng)的靜態(tài)社團(tuán)發(fā)現(xiàn)算法已經(jīng)不能滿足在動態(tài)變化的網(wǎng)絡(luò)中準(zhǔn)確挖掘社團(tuán)結(jié)構(gòu)的需求。相比于靜態(tài)網(wǎng)絡(luò)的社團(tuán)發(fā)現(xiàn)，動態(tài)社團(tuán)發(fā)現(xiàn)算法的設(shè)計(jì)更具有挑戰(zhàn)性，主要有以下幾點(diǎn)原因。首先，動態(tài)網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)不僅要考慮社團(tuán)結(jié)構(gòu)的劃分是否準(zhǔn)確，還要充分考慮動態(tài)網(wǎng)絡(luò)的演化過程。例如，圖1（a）為靜態(tài)社團(tuán)發(fā)現(xiàn)示意圖，網(wǎng)絡(luò)中的節(jié)點(diǎn)根據(jù)連接的緊密程度被劃分為3個社團(tuán)。對于動態(tài)網(wǎng)絡(luò)的社團(tuán)發(fā)現(xiàn)，圖1（b）的上下兩部分分別表示t和t-1時刻的網(wǎng)絡(luò)快照Gt和Gt-1。在t時刻有兩種社團(tuán)劃分策略，分別用劃分1和2兩條虛線表示。如果不考慮網(wǎng)絡(luò)的動態(tài)演化，劃分策略1和2在t時刻擁有相同的社團(tuán)劃分質(zhì)量。但是，如果考慮網(wǎng)絡(luò)的動態(tài)演化，劃分策略2要好于策略1。因?yàn)閯澐植呗?在t和t－1時刻的劃分更相近，所以相比于劃分策略1更加合理。所以，動態(tài)網(wǎng)絡(luò)的社團(tuán)發(fā)現(xiàn)既要考慮每個時刻的社團(tuán)發(fā)現(xiàn)質(zhì)量還要考慮動態(tài)網(wǎng)絡(luò)的演化過程。其次，動態(tài)社團(tuán)發(fā)現(xiàn)的另一個挑戰(zhàn)是解的不穩(wěn)定性問題。無法確定劃分結(jié)果的變化是由社團(tuán)的自然演化引起的，還是由于網(wǎng)絡(luò)中噪聲或算法不穩(wěn)定性造成的。對此，研究者們提出了大量的解決方案，其最終目標(biāo)是使社團(tuán)的演化更加平滑。為了解決這個問題，Chakrabarti等人［5］提出了演化聚類框架，該框架是目前應(yīng)用最廣泛的動態(tài)社團(tuán)發(fā)現(xiàn)方法之一。其假設(shè)在短時間內(nèi)聚類的突然變化可能是由噪聲引起的，并且不期望聚類發(fā)生突然變化。Pallaet等人［6］通過研究科學(xué)家合作網(wǎng)絡(luò)的動態(tài)演變過程，發(fā)現(xiàn)在短時間內(nèi)社團(tuán)不會發(fā)生劇烈的變化，并且提出社團(tuán)發(fā)生大規(guī)模演化后，社團(tuán)的生命周期將會更長。這證明了演化聚類模型的假設(shè)與現(xiàn)實(shí)網(wǎng)絡(luò)的特質(zhì)相吻合。最后，捕捉動態(tài)的社團(tuán)演化模式對于理解動態(tài)網(wǎng)絡(luò)深層特征和演化方向至關(guān)重要。如何捕捉動態(tài)網(wǎng)絡(luò)中的社團(tuán)演化模式和過程、跟蹤動態(tài)演化進(jìn)程是動態(tài)社團(tuán)發(fā)現(xiàn)面臨的重要挑戰(zhàn)。

雖然研究者們對于動態(tài)網(wǎng)絡(luò)的社團(tuán)發(fā)現(xiàn)方法付出了巨大的努力，但仍有許多問題有待解決。a）已提出的大多數(shù)方法并沒有利用重要的先驗(yàn)信息來提高社團(tuán)發(fā)現(xiàn)的準(zhǔn)確率。b）在動態(tài)網(wǎng)絡(luò)中，社團(tuán)結(jié)構(gòu)和時間演化特征是同步存在的，捕捉社團(tuán)的演化過程有助于從本質(zhì)上理解動態(tài)網(wǎng)絡(luò)的演化模式。然而，大多數(shù)動態(tài)社團(tuán)發(fā)現(xiàn)算法未對社團(tuán)的動態(tài)演化過程直接進(jìn)行建模，從而無法描述和可視化社團(tuán)的演化過程。c）大多數(shù)基于演化聚類的算法只適用于社團(tuán)和節(jié)點(diǎn)個數(shù)不發(fā)生改變的場景。然而，節(jié)點(diǎn)的加入和離開，社團(tuán)的新增和減少是網(wǎng)絡(luò)中常見的動態(tài)變化場景。如何在演化聚類框架中處理社團(tuán)和節(jié)點(diǎn)數(shù)量發(fā)生變化的情況是一個亟需解決的問題。

針對以上問題和挑戰(zhàn)，本文提出了一個強(qiáng)大、可解釋的動態(tài)網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)框架EC-DCD來挖掘動態(tài)網(wǎng)絡(luò)中的社團(tuán)結(jié)構(gòu)，其主要框架如圖2所示。EC-DCD算法不僅能夠準(zhǔn)確地挖掘動態(tài)網(wǎng)絡(luò)中的社團(tuán)結(jié)構(gòu)，還可以同步捕捉社團(tuán)的演化模式，實(shí)現(xiàn)社團(tuán)演化過程的可視化。在動態(tài)變化的網(wǎng)絡(luò)中，個別節(jié)點(diǎn)的變動存在隨機(jī)性，所以網(wǎng)絡(luò)中往往存在大量噪聲。首先，為了抑制噪聲對社團(tuán)發(fā)現(xiàn)結(jié)果的影響，EC-DCD算法將t－1時刻的社團(tuán)發(fā)現(xiàn)結(jié)果作為t時刻的先驗(yàn)信息，從而提高社團(tuán)發(fā)現(xiàn)的準(zhǔn)確率。然后基于演化聚類框架，通過對鄰接矩陣進(jìn)行非負(fù)矩陣分解獲得社團(tuán)指示矩陣來評價當(dāng)前時刻的社團(tuán)發(fā)現(xiàn)質(zhì)量。為了分析社團(tuán)演化過程，本文對社團(tuán)演化模式進(jìn)行建模，假設(shè)在每個時刻存在一個演化模式，將其表示為一個隨時間變化的社團(tuán)演化矩陣。并利用演化矩陣來評價當(dāng)前時刻與歷史時刻社團(tuán)劃分結(jié)果的符合度。

總的來說，本文的主要貢獻(xiàn)如下：

a）算法利用前一時刻的社團(tuán)發(fā)現(xiàn)結(jié)果作為先驗(yàn)信息優(yōu)化當(dāng)前的網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)，從而減少網(wǎng)絡(luò)噪聲和毫無根據(jù)的網(wǎng)絡(luò)演化對社團(tuán)劃分的影響，提高社團(tuán)發(fā)現(xiàn)的準(zhǔn)確度；

b）基于演化聚類框架，利用NMF模型得到動態(tài)網(wǎng)絡(luò)中每個時刻準(zhǔn)確的社團(tuán)結(jié)構(gòu)，同時平滑連續(xù)兩個時刻的社團(tuán)發(fā)現(xiàn)結(jié)果；

c）對動態(tài)社團(tuán)的演化模式進(jìn)行建模，引入社團(tuán)演化矩陣對社團(tuán)的演化模式進(jìn)行捕捉和跟蹤，同時實(shí)現(xiàn)對社團(tuán)演化過程的分析和可視化；

d）在多個真實(shí)和人工數(shù)據(jù)集上進(jìn)行了大量實(shí)驗(yàn)，實(shí)驗(yàn)結(jié)果證明EC-DCD與對比算法相比，獲得了準(zhǔn)確并且穩(wěn)定的社團(tuán)發(fā)現(xiàn)性能，同時實(shí)現(xiàn)了對社團(tuán)演化過程的可視化。

1 相關(guān)工作

近年來，涌現(xiàn)出了大量方法用于解決動態(tài)網(wǎng)絡(luò)中的社團(tuán)發(fā)現(xiàn)問題。可以將這些方法分為增量聚類方法和演化聚類方法。

增量聚類算法［7～14］嘗試將靜態(tài)網(wǎng)絡(luò)的社團(tuán)發(fā)現(xiàn)方法擴(kuò)展到動態(tài)網(wǎng)絡(luò)中，其主要思想是利用靜態(tài)社團(tuán)發(fā)現(xiàn)方法在第一個網(wǎng)絡(luò)快照中發(fā)現(xiàn)社團(tuán)結(jié)構(gòu)，然后根據(jù)連續(xù)兩個時刻快照之間節(jié)點(diǎn)和邊的動態(tài)變化來劃分后續(xù)快照的社團(tuán)結(jié)構(gòu)，當(dāng)前時刻的社團(tuán)結(jié)構(gòu)是從前一時刻的社團(tuán)結(jié)構(gòu)中推導(dǎo)而來。代表算法有IA-MCS［7］、GraphScope［8］等。增量聚類方法可以直接使用靜態(tài)的社團(tuán)發(fā)現(xiàn)算法，比較容易實(shí)現(xiàn)。然而，增量聚類算法忽略了噪聲對每個時刻社團(tuán)發(fā)現(xiàn)的影響，從長期和全局角度來看，這種方法不能保證社團(tuán)發(fā)現(xiàn)結(jié)果的一致性。

演化聚類算法［15～29］是目前最流行的一種動態(tài)網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)方法，最早被Chakrabarti等人［5］提出用于流數(shù)據(jù)的聚類，通過將其應(yīng)用于K-means和凝聚層次聚類算法以處理不斷變化的數(shù)據(jù)。演化聚類框架假設(shè)短時間內(nèi)的聚類結(jié)果不會發(fā)生劇烈變化，網(wǎng)絡(luò)的突變多是由于噪聲引起的，并引入時間損失函數(shù)對下一時刻突變的社團(tuán)劃分進(jìn)行懲罰。Chi等人［18］首次將演化聚類算法用于動態(tài)網(wǎng)絡(luò)的社團(tuán)發(fā)現(xiàn)問題，通過快照代價（snapshot cost，CS）來評價當(dāng)前時刻社團(tuán)發(fā)現(xiàn)的準(zhǔn)確度，通過時間代價（temporal cost，CT）來度量連續(xù)兩個時刻社團(tuán)發(fā)現(xiàn)結(jié)果的相似性。以演化聚類框架為基礎(chǔ)，Lin等人［19］提出了時間平滑（temporal smoothness）框架用于動態(tài)網(wǎng)絡(luò)的社團(tuán)發(fā)現(xiàn)，并提出了研究社團(tuán)動態(tài)演化的統(tǒng)一框架FacetNet，該算法是目前最經(jīng)典且廣泛使用的動態(tài)社團(tuán)發(fā)現(xiàn)算法。FacetNet采用隨機(jī)塊模型生成社團(tuán)，并通過一個健壯的統(tǒng)一過程來分析社團(tuán)及其演化，該過程考慮了社團(tuán)演化過程和演化的時間平滑性。隨后，F(xiàn)olino等人［20］提出了一種基于多目標(biāo)優(yōu)化的演化聚類算法DYNMOGA，該算法將快照代價和時間代價看做一個多目標(biāo)函數(shù)，在最大化快照代價的同時最小化時間代價。ECGNMF算法［21］通過NMF框架擬合每個時間片的社團(tuán)發(fā)現(xiàn)情況，從而獲得每個時刻的社團(tuán)結(jié)構(gòu)。對于時間代價，算法不僅考慮了介觀社團(tuán)歷史信息，還考慮了節(jié)點(diǎn)的微觀變化信息，通過引入正則化項(xiàng)對兩個連續(xù)時間的微觀節(jié)點(diǎn)變化進(jìn)行約束，平滑連續(xù)時間內(nèi)微觀節(jié)點(diǎn)的變化情況。Ma等人［23］提出了一種基于共同正則化非負(fù)矩陣分解的動態(tài)網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)算法Cr-ENMF，該算法利用前一時刻的網(wǎng)絡(luò)和社團(tuán)結(jié)構(gòu)來表征時間代價，并將其通過正則化項(xiàng)加入到目標(biāo)函數(shù)中，成功挖掘動態(tài)網(wǎng)絡(luò)中的社團(tuán)結(jié)構(gòu)。Wang等人［24］提出了一種新的動態(tài)圖正則化對稱非負(fù)矩陣分解方法DGR-SNMF，該方法引入網(wǎng)絡(luò)的幾何結(jié)構(gòu)來表征網(wǎng)絡(luò)拓?fù)湓诙虝r間內(nèi)的時間平滑性，巧妙地通過把圖正則化項(xiàng)作為時間代價函數(shù)，將幾何結(jié)構(gòu)信息充分融合到社團(tuán)發(fā)現(xiàn)過程中。Li等人［25］將圖嵌入引入動態(tài)網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)中，利用前一時刻、當(dāng)前時刻和下一個時刻的網(wǎng)絡(luò)快照設(shè)計(jì)三階平滑策略，充分表征社團(tuán)演化。雖然已提出的算法實(shí)現(xiàn)了對動態(tài)網(wǎng)絡(luò)的社團(tuán)結(jié)構(gòu)挖掘，但大多數(shù)算法未對社團(tuán)的動態(tài)演化模式進(jìn)行直接建模，從而無法描述和可視化社團(tuán)的演化過程。由此可知，基于演化聚類框架的社團(tuán)發(fā)現(xiàn)方法的主要挑戰(zhàn)是如何平衡快照代價CS和時間代價CT，以及如何量化時間代價CT并對社團(tuán)演化模式進(jìn)行建模。

2 相關(guān)定義

2.1 符號

對于一個隨時間演化的動態(tài)網(wǎng)絡(luò)，本文將其表示為一系列時刻{1，2，…，T}的網(wǎng)絡(luò)序列快照Gt={G1，G2，…，GT}，T為快照數(shù)量。其中，Gt=（Vt，Et）表示t時刻的網(wǎng)絡(luò)快照，Vt為t時刻的節(jié)點(diǎn)集合，Et為t時刻節(jié)點(diǎn)之間邊的集合。本文用網(wǎng)絡(luò)快照對應(yīng)的鄰接矩陣At={A1，A2，…，AT}表示動態(tài)網(wǎng)絡(luò)，其中At=（aij，t）n×n×T表示t時刻的網(wǎng)絡(luò)快照，n為節(jié)點(diǎn)數(shù)量，如果節(jié)點(diǎn)vi和vj在t時刻有連接，則aij，t=1，否則aij，t=0。表1總結(jié)了本文所用的符號及定義。

給定一個動態(tài)網(wǎng)絡(luò)Gt={G1，G2，…，GT}，動態(tài)網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)的目標(biāo)為：a）對當(dāng)前時刻的網(wǎng)絡(luò)快照進(jìn)行準(zhǔn)確的社團(tuán)結(jié)構(gòu)挖掘，將網(wǎng)絡(luò)中的節(jié)點(diǎn)劃分為k個社團(tuán)，使社團(tuán)發(fā)現(xiàn)結(jié)果與真實(shí)的社團(tuán)結(jié)構(gòu)盡可能相同。動態(tài)網(wǎng)絡(luò)的社團(tuán)結(jié)構(gòu)由每個時刻社團(tuán)的集合構(gòu)成Ct={C1，C2，…，CK}；b）連續(xù)時刻的社團(tuán)發(fā)現(xiàn)結(jié)果Ct和Ct-1不會發(fā)生劇烈變化，社團(tuán)的演化是平滑的；c）建立描述社團(tuán)演化生命周期的進(jìn)化鏈，對社團(tuán)演化模式進(jìn)行建模，實(shí)現(xiàn)社團(tuán)演化過程的跟蹤和分析。

2.2 演化聚類框架

演化聚類框架假設(shè)社團(tuán)結(jié)構(gòu)在短時間內(nèi)不會發(fā)生突變，連續(xù)兩個時刻的社團(tuán)結(jié)構(gòu)演化具有平滑性。演化聚類框架由快照代價CS和時間代價CT的線性組合構(gòu)成。其中，CS用于衡量t時刻社團(tuán)發(fā)現(xiàn)結(jié)果Ct與真實(shí)社團(tuán)結(jié)構(gòu)的相符程度，CT用于衡量t時刻社團(tuán)發(fā)現(xiàn)結(jié)果Ct與t－1時刻社團(tuán)發(fā)現(xiàn)結(jié)果Ct-1之間的差異。基于演化聚類的動態(tài)網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)方法需要滿足兩個條件：一是社團(tuán)劃分結(jié)果應(yīng)該盡可能準(zhǔn)確地表示當(dāng)前的網(wǎng)絡(luò)結(jié)構(gòu)；二是連續(xù)兩個時刻，社團(tuán)發(fā)現(xiàn)的結(jié)果是平滑的，沒有顯著的突變。演化聚類的最終目標(biāo)是在兩個子模塊之間取得平衡：

Cost=α·CS+（1－α）·CT（1）

其中：α∈（0，1）為權(quán)重系數(shù)，用于平衡CS和CT的權(quán)重比例。當(dāng)α=1時，方法返回的結(jié)果為沒有考慮連續(xù)時刻的社團(tuán)演化特征，動態(tài)社團(tuán)發(fā)現(xiàn)問題等價于靜態(tài)社團(tuán)發(fā)現(xiàn)問題。當(dāng)α=0時，框架得到與上一時刻相同的社團(tuán)發(fā)現(xiàn)結(jié)果，即CRt=CRt－1。

3 EC-DCD模型

3.1 快照代價

對于快照代價CS部分，EC-DCD期望在當(dāng)前時刻獲得與真實(shí)社團(tuán)結(jié)構(gòu)相符的社團(tuán)劃分。首先引入社團(tuán)指示矩陣H∈Euclid ExtraaBpn×k，如果兩個節(jié)點(diǎn)屬于同一個社團(tuán)，那么它們之間生成邊的概率很高。因此，本文期望HHT的每個元素都盡可能和網(wǎng)絡(luò)鄰接矩陣A相接近。假設(shè)網(wǎng)絡(luò)中節(jié)點(diǎn)之間邊數(shù)的期望HHT和鄰接矩陣A中可觀察邊數(shù)之間的誤差服從均值為0、標(biāo)準(zhǔn)差為σ的高斯分布：

aij－∑khikhjk～N（0，σ2）（2）

根據(jù)高斯概率密度函數(shù)，得到其似然函數(shù)為

L=∏i≠j12πσ（－12（aij－∑khikhjkσ）2）（3）

最大化L等于最大化log L：

log L=∑ij-12（aij－∑khikhjk）2+c=

－12（∑ij（aij－∑khikhjk）2）+c（4）

因?yàn)椤珹－HHT‖2F=∑ij（aij－∑khikhjk）2，所以目標(biāo)函數(shù)為

L（A，H）=‖A－HHT‖2F（5）

其中：‖A‖2F=∑ni=1 ∑dj=1|aij|2。在本節(jié)中，Ht是t時刻的社團(tuán)指示矩陣，Ht的每一行表示在t時刻節(jié)點(diǎn)屬于每個社團(tuán)的隸屬度情況，其中him，t代表t時刻節(jié)點(diǎn)vi隸屬于社團(tuán)cm的概率。可以推導(dǎo)出him，thjm，t是節(jié)點(diǎn)vi和vj在t時刻在社團(tuán)cm內(nèi)連接邊數(shù)的期望，∑klhil，thjl，t為整個網(wǎng)絡(luò)中節(jié)點(diǎn)vi和vj在t時刻連接邊數(shù)的期望，所以HtHTt代表在t時刻任意兩個節(jié)點(diǎn)之間生成邊的期望。本文期望t時刻的社團(tuán)發(fā)現(xiàn)結(jié)果盡可能和t時刻的鄰接矩陣At相似。因此，快照成本CS函數(shù)如下：

CS=‖At-HtHTt‖2F（6）

3.2 時間代價

對于時間代價，演化聚類框架假設(shè)連續(xù)兩個時刻的社團(tuán)結(jié)構(gòu)演化是平滑的，不會發(fā)生劇烈改變。因此，本文假設(shè)節(jié)點(diǎn)歸屬的社團(tuán)在連續(xù)兩個時刻不會發(fā)生劇烈變化，節(jié)點(diǎn)在t－1時刻屬于社團(tuán)ci，那么它有很大的概率在t時刻也屬于社團(tuán)ci。為了進(jìn)一步探索和分析動態(tài)網(wǎng)絡(luò)的時間演化模式，本文引入社團(tuán)演化矩陣Gt∈Euclid ExtraaBpk×k對社團(tuán)演化模式進(jìn)行建模。通過對社團(tuán)演化矩陣的分析可以捕獲社團(tuán)演化趨勢、預(yù)測社團(tuán)活動和實(shí)現(xiàn)對社團(tuán)演化過程的可視化，從而實(shí)現(xiàn)對社團(tuán)動態(tài)演化過程的跟蹤和分析。其中，矩陣Gt的元素gij，t表示節(jié)點(diǎn)在t時刻從社團(tuán)ci轉(zhuǎn)移到社團(tuán)cj的概率。因此，節(jié)點(diǎn)在t時刻隸屬于社團(tuán)的情況Ht，應(yīng)該由t－1時刻節(jié)點(diǎn)隸屬于社團(tuán)的情況Ht－1和社團(tuán)轉(zhuǎn)移概率Gt共同演化而來。節(jié)點(diǎn)vi在t－1時刻隸屬于社團(tuán)cl的概率hil，t－1與t時刻節(jié)點(diǎn)vi從社團(tuán)cl轉(zhuǎn)移到社團(tuán)cm的概率glm，t的乘積應(yīng)該和t時刻節(jié)點(diǎn)vi屬于社團(tuán)cm的概率him，t盡可能相近，即him，t≈hil，t－1glm，t。因此，本文定義時間代價CT函數(shù)為

CT=‖Ht－1Gt－Ht‖2F（7）

3.3 先驗(yàn)信息

為了減少噪聲以及毫無根據(jù)的網(wǎng)絡(luò)演化對社團(tuán)發(fā)現(xiàn)結(jié)果的影響，算法將t－1時刻的社團(tuán)發(fā)現(xiàn)結(jié)果作為t時刻的先驗(yàn)信息來優(yōu)化t時刻的網(wǎng)絡(luò)拓?fù)洌瑥亩岣呱鐖F(tuán)發(fā)現(xiàn)的準(zhǔn)確度。先驗(yàn)信息定義為

A*t=At-β（Ht-1HTt-1）（8）

其中：A*t為優(yōu)化后t時刻的鄰接矩陣；β為先驗(yàn)信息的權(quán)重系數(shù)。基于此，通過式（8）將前一時刻的社團(tuán)發(fā)現(xiàn)信息作為當(dāng)前時刻的先驗(yàn)信息融合到演化聚類框架中，可以調(diào)整兩個連續(xù)時刻網(wǎng)絡(luò)拓?fù)渲g的平滑度，從而減少噪聲對社團(tuán)發(fā)現(xiàn)的影響，提高算法的精度。因此，最終的目標(biāo)函數(shù)為

minHt，Gt‖A*t-HtHTt‖2F+α‖Ht-1Gt-Ht‖2F "if t≥2

minHt‖At-HtHTt‖2F if t=1

s.t. （Ht）ij≥0， （Gt）ij≥0" i， j（9）

其中：α為權(quán)重系數(shù)，用于平衡快照代價和時間代價的權(quán)重比例。

4 模型優(yōu)化和分析

由于式（9）的求解是非凸優(yōu)化問題，很難求出全局最優(yōu)解。本文采用迭代優(yōu)化的方法求解目標(biāo)函數(shù)，通過固定其他變量來優(yōu)化一個變量。首先，為了推導(dǎo)式（9）在非負(fù)約束下的更新規(guī)則，分別引入拉格朗日乘子和ε，式（9）的拉格朗日函數(shù)為

當(dāng)t=1時，

5 EC-DCD算法

擴(kuò)展基于演化聚類框架的固有假設(shè)較為困難，多數(shù)基于演化聚類的算法都無法處理節(jié)點(diǎn)和社團(tuán)數(shù)量隨時間變化的場景。但在動態(tài)網(wǎng)絡(luò)中，節(jié)點(diǎn)和社團(tuán)的增加和減少是常見的情況。因此，本文針對社團(tuán)和節(jié)點(diǎn)發(fā)生變化的情況分別提出了相應(yīng)策略進(jìn)行解決。

a）處理網(wǎng)絡(luò)中節(jié)點(diǎn)變化的情況。針對網(wǎng)絡(luò)中節(jié)點(diǎn)個數(shù)發(fā)生增加和減少的情況，當(dāng)網(wǎng)絡(luò)中有新的節(jié)點(diǎn)加入時，在鄰接矩陣的行和列分別填充0。類似地，如果網(wǎng)絡(luò)中的節(jié)點(diǎn)減少，則將其對應(yīng)的行和列刪除。這樣，兩個矩陣變?yōu)橄嗤?guī)模，可以進(jìn)行之后的計(jì)算。通過此策略將模型擴(kuò)展到節(jié)點(diǎn)數(shù)量隨時間變化的情況。

b）處理網(wǎng)絡(luò)中社團(tuán)變化的情況。針對網(wǎng)絡(luò)中社團(tuán)發(fā)生變化的情況，本文引入以下規(guī)則來確定每個時刻的社團(tuán)個數(shù)kt：

kt=argmin "k‖∑ki=1ηiTsiTs′iT‖‖At‖gt;τ（21）

其中：ηiT是矩陣At的特征值；siT是特征值對應(yīng)的特征向量。矩陣At可以根據(jù)特征值和特征向量進(jìn)行重建，At=∑ki=1ηiTsiTs′iT。隨著特征向量的增加，At和特征分解之間的誤差‖At－∑ki=1ηiTsiTs′iT‖2變小。所以當(dāng)參數(shù)τ取適當(dāng)?shù)闹禃r，可以在特征值盡量小的情況下達(dá)到一個很好的平衡，從而確定社團(tuán)個數(shù)。參數(shù)τ是一個經(jīng)驗(yàn)值，根據(jù)文獻(xiàn)［20］，將τ設(shè)置為0.55。

此外，考慮到社團(tuán)結(jié)構(gòu)隨時間演化的平滑性，如果社團(tuán)數(shù)量在連續(xù)內(nèi)時間保持穩(wěn)定，則用Ht－1來更新Ht；當(dāng)連續(xù)內(nèi)社團(tuán)數(shù)發(fā)生變化，則進(jìn)行隨機(jī)初始化，而不使用前一時刻的社團(tuán)指示矩陣作為初始值。

算法1：EC-DCD算法

輸入：動態(tài)網(wǎng)絡(luò)序列Gt={G1，G2，…，GT}；參數(shù)α、γ。

輸出：每個時刻的網(wǎng)絡(luò)社團(tuán)劃分Ct={C1，C2，…，CT}。

for t=1， 2，…， T do

根據(jù)式（21）確定網(wǎng)絡(luò)中社團(tuán)個數(shù)

初始化Ht、Gt

if t=1 do

repeat

根據(jù)式（18）更新H1

until convergence

得到t=1時刻的社團(tuán)C1

else do

repeat

對于每個時刻t，根據(jù)式（8）計(jì)算先驗(yàn)信息A*t

根據(jù)式（19）更新Ht

根據(jù)式（20）更新Gt

until convergence

得到t時刻的社團(tuán)更新Ct

end for

6 實(shí)驗(yàn)結(jié)果分析

6.1 基準(zhǔn)方法

為了驗(yàn)證EC-DCD算法的有效性，實(shí)驗(yàn)選擇五個具有代表性的動態(tài)網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)算法作為對比算法，分別為FacetNet、DYNMOGA、DNMF、NE2NMF和CoDeDANet。

a）FacetNet［19］。FacetNet將快照代價定義為觀測到的節(jié)點(diǎn)相似性矩陣與用混合模型計(jì)算出的近似社團(tuán)結(jié)構(gòu)之間的KL散度，并將時間代價定義為t和t－1時刻社團(tuán)結(jié)構(gòu)劃分的差異。

b）DYNMOGA［20］。DYNMOGA首先最大化快照代價來度量社團(tuán)發(fā)現(xiàn)的質(zhì)量，然后計(jì)算兩個時刻社團(tuán)劃分的標(biāo)準(zhǔn)化互信息（NMI）來測量當(dāng)前時刻獲得的社團(tuán)結(jié)構(gòu)與前一個時刻獲得的社團(tuán)結(jié)構(gòu)之間的相似性。

c）DNMF［29］。DNMF利用全概率模型挖掘鄰接矩陣與NMF分解結(jié)果之間的歐幾里德距離，并對兩個連續(xù)快照中的矩陣分解結(jié)果進(jìn)行約束。

d）NE2NMF［25］。NE2NMF從多個角度充分刻畫社團(tuán)的動態(tài)變化，并通過分解每個時間快照的低維圖嵌入來減少運(yùn)行時間。

e）CoDeDANet［30］。CoDeDANet首先利用譜聚類獲得每個時刻的社團(tuán)結(jié)構(gòu)，然后利用張量同時考慮社團(tuán)當(dāng)前結(jié)構(gòu)和歷史結(jié)構(gòu)。

6.2 人工數(shù)據(jù)集性能分析

6.2.1 人工數(shù)據(jù)集1性能分析

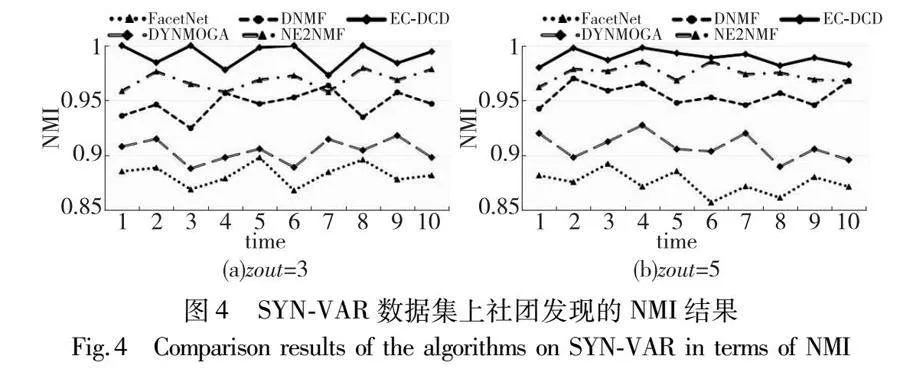
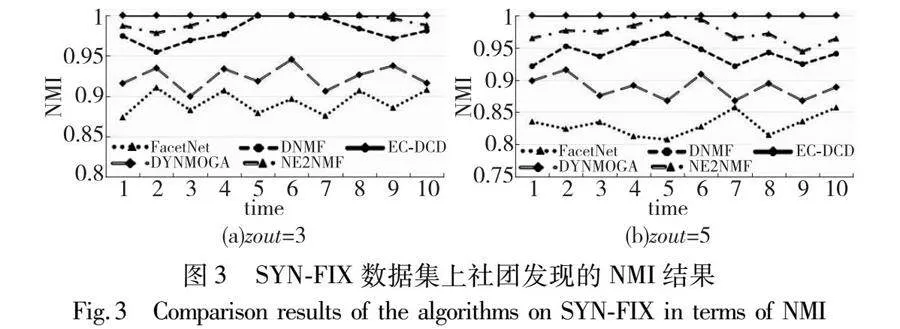
人工數(shù)據(jù)集1是文獻(xiàn)［25］使用的人工數(shù)據(jù)集，其中包含SYN-FIX和SYN-VAR兩種類型的動態(tài)網(wǎng)絡(luò)。SYN-FIX網(wǎng)絡(luò)由128個節(jié)點(diǎn)組成，所有節(jié)點(diǎn)被平均分為4個社團(tuán)，節(jié)點(diǎn)的平均度數(shù)為16，網(wǎng)絡(luò)中的節(jié)點(diǎn)與其他社團(tuán)的節(jié)點(diǎn)有zout條邊相連。本節(jié)實(shí)驗(yàn)分別設(shè)置zout=3和5，當(dāng)zout增加時，網(wǎng)絡(luò)中的噪聲水平也隨之增加，挖掘網(wǎng)絡(luò)中社團(tuán)結(jié)構(gòu)的難度加大。為了引入網(wǎng)絡(luò)的動態(tài)變化，SYN-FIX網(wǎng)絡(luò)在t－1時刻從每個社團(tuán)中隨機(jī)選擇3個節(jié)點(diǎn)，并在t時刻分配給其他社團(tuán)。SYN-FIX網(wǎng)絡(luò)在所有時刻的社團(tuán)數(shù)量不發(fā)生變化，社團(tuán)數(shù)量始終為4。SYN-VAR網(wǎng)絡(luò)由256個節(jié)點(diǎn)組成，所有節(jié)點(diǎn)被平均分為4個社團(tuán)，節(jié)點(diǎn)的平均度為16。同樣，本節(jié)將zout設(shè)置為3和5。不同于SYN-FIX網(wǎng)絡(luò)，SYN-VAR網(wǎng)絡(luò)通過社團(tuán)的新生和消亡來實(shí)現(xiàn)社團(tuán)的動態(tài)變化。SYN-VAR網(wǎng)絡(luò)在t－1時刻從每個社團(tuán)中隨機(jī)選擇8個節(jié)點(diǎn)，在t時刻將這些節(jié)點(diǎn)構(gòu)成一個新的社團(tuán)，連續(xù)5個時刻重復(fù)此過程，然后再經(jīng)過5個時刻將這些節(jié)點(diǎn)返回到原始社團(tuán)。圖3、4分別為算法在SYN-FIX和SYN-VAR數(shù)據(jù)集上的社團(tuán)發(fā)現(xiàn)結(jié)果。

從圖3、4可以得出，EC-DCD在SYN-FIX和SYN-VAR數(shù)據(jù)集上的所有時刻都取得了優(yōu)于其他基線算法的社團(tuán)發(fā)現(xiàn)結(jié)果。特別是在SYN-FIX網(wǎng)絡(luò)中，在zout=3和5兩種情況下，EC-DCD在10個時刻取得的NMI指標(biāo)值均為1，算法劃分的社團(tuán)結(jié)構(gòu)和真實(shí)社團(tuán)結(jié)構(gòu)完全相同。對于社團(tuán)個數(shù)發(fā)生變化的SYN-VAR網(wǎng)絡(luò)，EC-DCD也取得了所有時刻 NMI均大于0.96的優(yōu)異性能。相比于其他基線算法，EC-DCD不僅在2個數(shù)據(jù)集的所有時刻都取得了最好的社團(tuán)發(fā)現(xiàn)結(jié)果，而且社團(tuán)發(fā)現(xiàn)結(jié)果曲線比較平滑，相鄰時刻的社團(tuán)發(fā)現(xiàn)結(jié)果沒有突變，這說明本文方法不僅能夠準(zhǔn)確地發(fā)現(xiàn)真實(shí)的社團(tuán)結(jié)構(gòu)，而且在連續(xù)時刻的社團(tuán)劃分性能非常穩(wěn)定。

6.2.2 人工數(shù)據(jù)集2性能分析

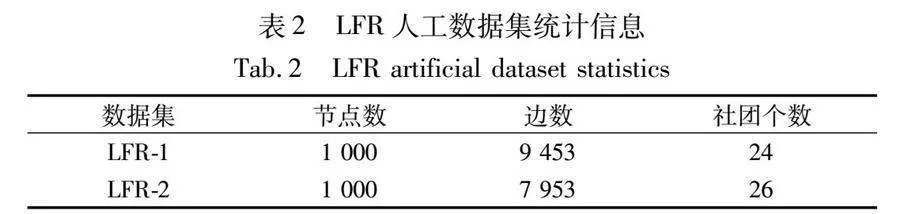
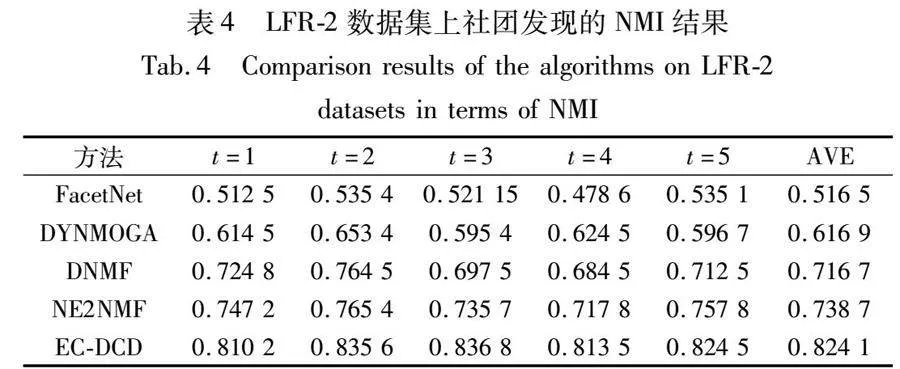
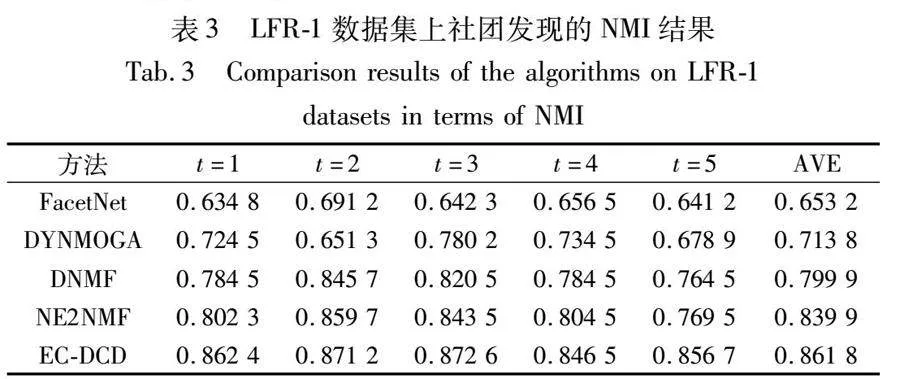
人工數(shù)據(jù)集2是基于LFR基準(zhǔn)［31］生成的冪律網(wǎng)絡(luò)。相比于人工數(shù)據(jù)集1，基于LFR基準(zhǔn)生成的數(shù)據(jù)集更加貼合真實(shí)網(wǎng)絡(luò)情況，發(fā)現(xiàn)社團(tuán)結(jié)構(gòu)的難度也更大。本節(jié)實(shí)驗(yàn)利用LFR基準(zhǔn)生成2個人工數(shù)據(jù)集作為初始網(wǎng)絡(luò)，詳細(xì)信息如表2所示。對于數(shù)據(jù)集通過以下兩種操作引入動態(tài)網(wǎng)絡(luò)生成5個時刻的網(wǎng)絡(luò)快照：a）不改變社團(tuán)的個數(shù)，從每個社團(tuán)中隨機(jī)選擇一定數(shù)量的節(jié)點(diǎn)離開原社團(tuán)，并隨機(jī)加入其他社團(tuán)；b）改變社團(tuán)個數(shù)，通過社團(tuán)的新生和消亡實(shí)現(xiàn)社團(tuán)的動態(tài)變化。對于LFR-1，通過第一種操作引入動態(tài)網(wǎng)絡(luò)。在每個時刻，從每個社團(tuán)中隨機(jī)選擇6個節(jié)點(diǎn)改變其連接，從而改變其所屬社團(tuán)情況。對于LFR-2，通過第二種操作引入動態(tài)網(wǎng)絡(luò)，在第2和3個時刻隨機(jī)選擇1個社團(tuán)分裂成2個社團(tuán)，并在第4和5個時刻選擇2個社團(tuán)合并成1個社團(tuán)。因此，網(wǎng)絡(luò)LFR-2在5個時刻社團(tuán)的個數(shù)分別為：26、27、28、27、26。EC-DCD與其他基線算法在5個時刻的NMI結(jié)果和所有時刻的平均NMI結(jié)果如表3、4所示。

雖然基于LFR基準(zhǔn)生成的人工數(shù)據(jù)集增加了社團(tuán)發(fā)現(xiàn)的難度，但EC-DCD仍然獲得了理想的社團(tuán)發(fā)現(xiàn)結(jié)果。與其他的基線算法相比，在所有數(shù)據(jù)集上的所有時刻均取得了最佳的性能。這主要得益于EC-DCD基于演化聚類框架，利用非負(fù)矩陣分解獲得當(dāng)前時刻社團(tuán)劃分結(jié)果，使其盡可能貼近當(dāng)前網(wǎng)絡(luò)的真實(shí)社團(tuán)結(jié)構(gòu)，同時引入社團(tuán)演化矩陣平滑連續(xù)時刻的社團(tuán)演化。不僅如此，EC-DCD還利用前一時刻的社團(tuán)劃分結(jié)果作為先驗(yàn)信息優(yōu)化當(dāng)前拓?fù)洌谔岣呱鐖F(tuán)劃分準(zhǔn)確度的同時平滑每個時刻的劃分結(jié)果。

6.3 真實(shí)數(shù)據(jù)集KIT-Email性能分析

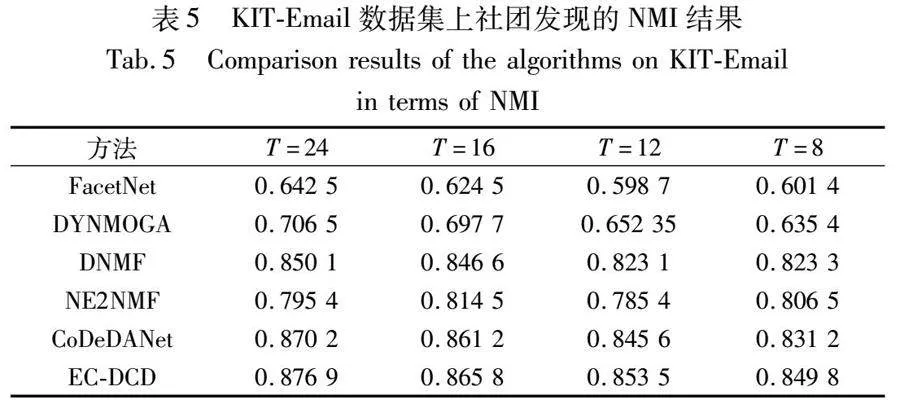
KIT-Email數(shù)據(jù)集（http：//i11www.iti.uni-karlsruhe.de/en/ projects/spp1307/emaildata）是由卡爾斯魯厄理工學(xué)院（Karlsruhe Institute of Technology，KIT）計(jì)算機(jī)科學(xué)系從2006年9月至2010年8月共48個月的電子郵件所構(gòu)成的電子郵件通信網(wǎng)絡(luò)。對于KIT-Email電子郵件網(wǎng)絡(luò)，節(jié)點(diǎn)是KIT計(jì)算機(jī)科學(xué)系的成員，邊的權(quán)重對應(yīng)兩個節(jié)點(diǎn)之間發(fā)送電子郵件的數(shù)量，計(jì)算機(jī)科學(xué)系的不同研究小組對應(yīng)不同社團(tuán)。本節(jié)分別以2、3、4和6個月為間隔分為幾個時間快照，其中T=24（連續(xù)2個月為一個網(wǎng)絡(luò)快照），T=16（連續(xù)3個月為一個網(wǎng)絡(luò)快照），T=12（連續(xù)4個月為一個網(wǎng)絡(luò)快照），T=8（連續(xù)6個月為一個網(wǎng)絡(luò)快照）。因?yàn)槁?lián)系人之間的聯(lián)系是稀疏的，所以實(shí)驗(yàn)選擇活躍的用戶構(gòu)成鄰接矩陣。其中，網(wǎng)絡(luò)中的節(jié)點(diǎn)數(shù)在138～231，社團(tuán)個數(shù)在23～27。每個時刻快照及所有時刻快照上的平均NMI作為社團(tuán)發(fā)現(xiàn)結(jié)果，如表5所示。

如表5所示，本文EC-DCD比其他方法獲得更好的性能。隨著快照數(shù)的減少，所有算法在NMI上的性能都趨于下降，因?yàn)殚g隔越短，數(shù)據(jù)點(diǎn)被視為孤立點(diǎn)的次數(shù)越多。所提EC-DCD在所有情況下都獲得了最優(yōu)的動態(tài)社團(tuán)劃分結(jié)構(gòu)，雖然表現(xiàn)次優(yōu)的CoDeDANet也利用張量充分考慮了歷史信息，但是本文方法對于噪聲具有魯棒性，更加穩(wěn)定。根據(jù)本文方法對動態(tài)郵件網(wǎng)絡(luò)的用戶進(jìn)行社團(tuán)劃分，可以發(fā)現(xiàn)經(jīng)常聯(lián)絡(luò)的郵件用戶群體，進(jìn)一步向不同分組提供感興趣的社交內(nèi)容，定向投放廣告等，給用戶提供更加穩(wěn)定優(yōu)質(zhì)的服務(wù)。不僅如此，通過分組可以識別出在動態(tài)變化的動態(tài)網(wǎng)絡(luò)中經(jīng)常通信的人，識別出網(wǎng)絡(luò)的關(guān)鍵節(jié)點(diǎn)，對網(wǎng)絡(luò)的穩(wěn)定性和信息傳播起著重要作用。對動態(tài)變化的動態(tài)郵件網(wǎng)絡(luò)進(jìn)行社團(tuán)發(fā)現(xiàn)，能夠幫助優(yōu)化資源分配，更好地配置網(wǎng)絡(luò)資源以滿足經(jīng)常通信群體的需求，提高網(wǎng)絡(luò)的效率和性能。

6.4 真實(shí)數(shù)據(jù)集CPC性能分析

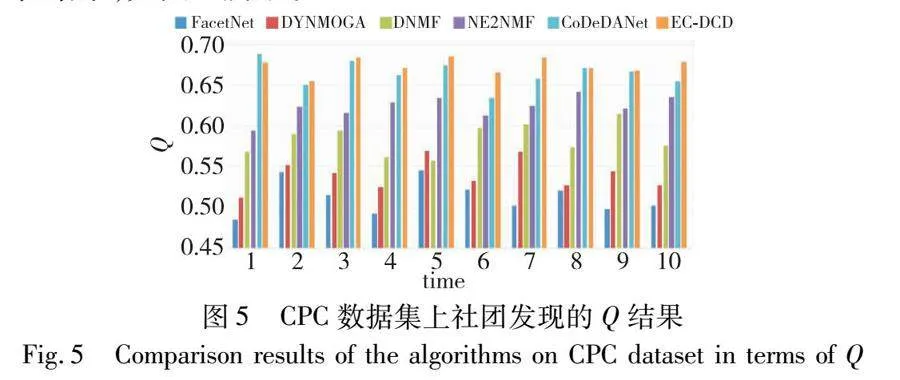
CPC數(shù)據(jù)集由Paraiso運(yùn)動成員之間在2006年6月中10天的手機(jī)通話記錄組成。該網(wǎng)絡(luò)的節(jié)點(diǎn)為全網(wǎng)唯一的手機(jī)號，兩個手機(jī)之間的呼叫構(gòu)成網(wǎng)絡(luò)中的邊。由此，可生成包含10個時刻的動態(tài)網(wǎng)絡(luò)序列，每個時刻的網(wǎng)絡(luò)為每天400個節(jié)點(diǎn)之間相互通信形成的網(wǎng)絡(luò)。由于數(shù)據(jù)集真實(shí)的社團(tuán)結(jié)構(gòu)是未知的，本文使用模塊度Q來衡量社團(tuán)發(fā)現(xiàn)的有效性，在CPC手機(jī)通信網(wǎng)絡(luò)數(shù)據(jù)上每種方法進(jìn)行10次實(shí)驗(yàn)，取平均結(jié)果作為實(shí)驗(yàn)結(jié)果，如圖5所示。

從圖5可以看到，EC-DCD在除第一個沒有歷史幾何結(jié)構(gòu)信息可用的網(wǎng)絡(luò)之外的其他所有網(wǎng)絡(luò)快照中都得到了最佳的性能，表現(xiàn)為具有更大的模塊度值。CoDeDANet雖然在第一個時刻利用了譜聚類方法獲得了最佳模塊度，但在之后的時刻，性能沒有EC-DCD好，這主要因?yàn)镋C-DCD不僅充分利用了歷史演化信息，還利用先驗(yàn)信息減少了噪聲對于社團(tuán)劃分結(jié)果的影響。通過所提算法對用戶類別進(jìn)行識別分組，有助于分析用戶通信模式和特征，從而提供定向的推薦服務(wù)和安全布控。具體地，通過對動態(tài)網(wǎng)絡(luò)進(jìn)行社團(tuán)發(fā)現(xiàn)，可以更好地了解他們之間的通信模式和頻率，從而更好地監(jiān)測和分析網(wǎng)絡(luò)中的信息傳播和交互模式。除此之外，將經(jīng)常通信的人劃分到一個組可以幫助進(jìn)行更精細(xì)化的安全管理，有助于提高網(wǎng)絡(luò)的安全性，防范潛在的安全風(fēng)險和威脅。

6.5 社團(tuán)演化模式分析

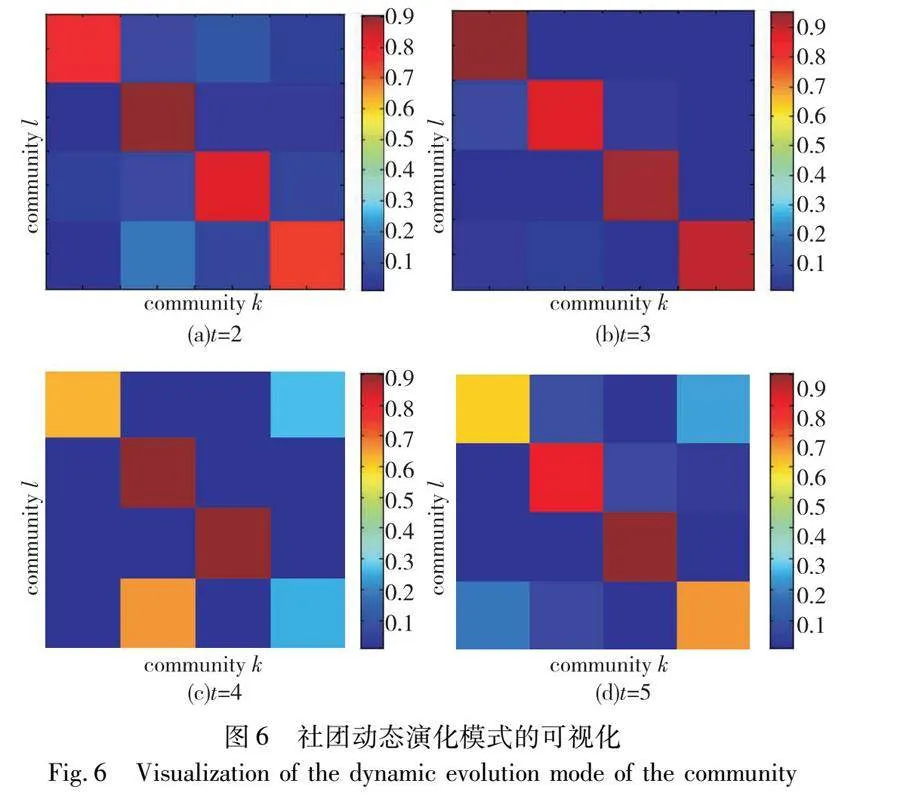
EC-DCD通過引入社團(tuán)演化矩陣Gt對社團(tuán)動態(tài)演化模式進(jìn)行建模，矩陣Gt的元素glk，t表示在t時刻節(jié)點(diǎn)從社團(tuán)l轉(zhuǎn)移到社團(tuán)k的概率，其量化了節(jié)點(diǎn)在社團(tuán)之間轉(zhuǎn)移的趨勢。為了分析動態(tài)網(wǎng)絡(luò)中社團(tuán)演化的模式，本節(jié)在人工數(shù)據(jù)集2上對連續(xù)4個時刻的社團(tuán)演化過程進(jìn)行可視化，進(jìn)一步分析社團(tuán)的演化過程。其中，在人工數(shù)據(jù)集2中設(shè)置zout=4，C=10%，并生成5個時刻的動態(tài)網(wǎng)絡(luò)。

圖6展示了連續(xù)4個時刻社團(tuán)演化過程的可視化結(jié)果，在圖6中，y軸為當(dāng)前時刻的社團(tuán)標(biāo)簽k，x軸為下一個時刻的節(jié)點(diǎn)所屬社團(tuán)標(biāo)簽l，每個方格的顏色代表節(jié)點(diǎn)從社團(tuán)k轉(zhuǎn)移到社團(tuán)l的概率，其值分別對應(yīng)轉(zhuǎn)移概率矩陣G中元素的值。如圖6所示，圖中對角線的值始終大于其他格子，這表示在大多數(shù)情況下，相比于轉(zhuǎn)移到其他社團(tuán)，節(jié)點(diǎn)在下一時刻有較大概率繼續(xù)保留在當(dāng)前社團(tuán)，這也間接證明了社團(tuán)演化的平滑性。但隨著網(wǎng)絡(luò)的持續(xù)演化，網(wǎng)絡(luò)中的社團(tuán)結(jié)構(gòu)也會發(fā)生變化。

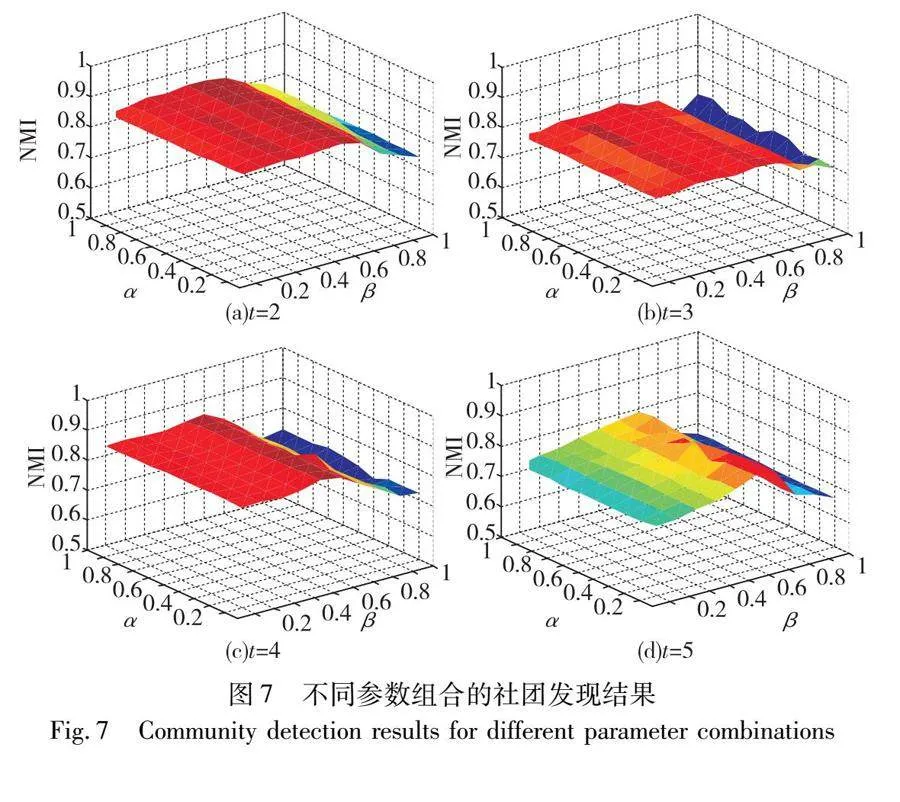
6.6 參數(shù)分析討論

本節(jié)對算法參數(shù)α和β的敏感度進(jìn)行討論，分別將其設(shè)置為{0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，1}，通過不同的參數(shù)組合來觀察EC-DCD在LFR-1網(wǎng)絡(luò)上的社團(tuán)發(fā)現(xiàn)性能。圖7分顯示了EC-DCD在不同參數(shù)組合下的社團(tuán)發(fā)現(xiàn)結(jié)果。可以從圖7得到結(jié)論，當(dāng)0.2≤α≤0.8和0.2≤β≤0.6時，EC-DCD取得了比較優(yōu)異并且平穩(wěn)的性能。

7 結(jié)束語

本文針對復(fù)雜網(wǎng)絡(luò)不斷演化的動態(tài)特性，對動態(tài)網(wǎng)絡(luò)中的社團(tuán)結(jié)構(gòu)挖掘問題展開了研究，提出了一種基于演化聚類的動態(tài)網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)算法EC-DCD。該算法利用NMF框架使當(dāng)前時刻的社團(tuán)劃分結(jié)果盡可能貼近真實(shí)的社團(tuán)結(jié)構(gòu)，同時保證相鄰時刻的社團(tuán)結(jié)構(gòu)演化具有平滑性。為了探索社團(tuán)的演化模式，算法引入社團(tuán)演化矩陣對社團(tuán)演化過程進(jìn)行直接建模，實(shí)現(xiàn)對社團(tuán)演變過程的跟蹤和分析。此外，EC-DCD利用前一時刻的社團(tuán)劃分結(jié)果作為先驗(yàn)信息對當(dāng)前的網(wǎng)絡(luò)拓?fù)浣Y(jié)構(gòu)進(jìn)行優(yōu)化，從而減少噪聲對社團(tuán)結(jié)構(gòu)挖掘的影響，進(jìn)一步提高社團(tuán)發(fā)現(xiàn)的準(zhǔn)確度。實(shí)驗(yàn)證明，EC-DCD在各種類型的人工數(shù)據(jù)集和真實(shí)數(shù)據(jù)集上都取得了優(yōu)異的社團(tuán)劃分性能，并且實(shí)現(xiàn)了對社團(tuán)演化過程的可視化。

隨著網(wǎng)絡(luò)規(guī)模和數(shù)據(jù)維度的不斷擴(kuò)大，需要更強(qiáng)大的技術(shù)來保持有效和高效的性能以及可行的計(jì)算速度。近年來，深度學(xué)習(xí)在社會計(jì)算領(lǐng)域發(fā)展迅速，其中圖神經(jīng)網(wǎng)絡(luò)將深度學(xué)習(xí)的方法應(yīng)用到非歐氏空間結(jié)構(gòu)的數(shù)據(jù)中，對社團(tuán)結(jié)構(gòu)挖掘和網(wǎng)絡(luò)表示與建模都具有重要的意義。在未來的研究中，可以引入圖神經(jīng)網(wǎng)絡(luò)等先進(jìn)深度學(xué)習(xí)技術(shù)實(shí)現(xiàn)動態(tài)網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)。

參考文獻(xiàn)：

［1］潘雨， 鄒軍華， 王帥輝， 等. 基于網(wǎng)絡(luò)表示學(xué)習(xí)的深度社團(tuán)發(fā)現(xiàn)方法［J］. 計(jì)算機(jī)科學(xué)， 2021， 48（11A）： 198-203. （Pan Yu， Zou Junhua， Wang Shuaihui， et al. Deep community discovery method based on network representation learning［J］. Computer Science， 2021， 48（11A）： 198-203.）

［2］潘雨， 王帥輝， 張磊， 等. 復(fù)雜網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)綜述 ［J］. 計(jì)算機(jī)科學(xué)， 2022， 49（11A）： 208-218. （Pan Yu， Wang Shuaihui， Zhang Lei， et al. A review on the discovery of complex network societies ［J］. Computer Science， 2022， 49（11A）： 208-218.）

［3］潘雨， 胡谷雨， 王帥輝， 等. 基于約束非負(fù)矩陣分解的符號網(wǎng)絡(luò)社團(tuán)發(fā)現(xiàn)方法 ［J］. 計(jì)算機(jī)應(yīng)用研究， 2020， 37（S2）： 82-86. （Pan Yu， Hu Guyu， Wang Shuaihui， et al. Community discovery method for symbolic networks based on constrained non-negative matrix decomposition ［J］. Application Research of Computers， 2020， 37（S2）： 82-86.）

［4］Rossetti G， Cazabet， Rémy. Community discovery in dynamic networks： a survey［J］. ACM Computing Surveys， 2017， 51（2）： 1-37.

［5］Chakrabarti D， Kumar R， Tomkins A. Evolutionary clustering［C］// Proc of the 12th ACM SIGKDD International Conference on Know-ledge Discovery and Data Mining. New York： ACM Press， 2006： 554-560.

［6］Palla G， Barabási A L， Vicsek T. Quantifying social group evolution［J］. Nature， 2007， 446（7136）： 664-667.

［7］Zhuang Di. Modularity-based dynamic community detection ［J］. IEEE Trans on Knowledge and Data Engineering， 2017， 33： 1934-1945.

［8］Karaaslanl Abdullah， Aviyente S. Community detection in dynamic networks： equivalence between stochastic blockmodels and evolutiona-ry spectral clustering ［J］. IEEE Trans on Signal and Information Processing over Networks， 2021， 7： 130-143.

［9］Xu Cong， Lee T C M. Statistical consistency for change point detection and community estimation in time-evolving dynamic networks ［J］. IEEE Trans on Signal and Information Processing over Networks， 2022， 8： 215-227.

［10］Zhuang Di， Chang J M， Li Mingchen. DynaMo： dynamic community detection by incrementally maximizing modularity［J］. IEEE Trans on Knowledge and Data Engineering， 2021， 33（5）： 1934-1945.

［11］Yang Bo， Liu Dayou. Force-based incremental algorithm for mining community structure in dynamic network［J］. Journal of Computer Science and Technology， 2006， 21（3）： 393-440.

［12］Guo Kun， He Ling， Huang Jiangsheng， et al. A local dynamic community detection algorithm based on node contribution ［C］// Proc of Conference on Computer Supported Cooperative Work. Singapore： Springer， 2019： 363-376.

［13］Wu Zhenyu， Chen Jiaying， Zhang Yinuo. An incremental community detection method in social big data［C］// Proc of the 5th International Conference on Big Data Computing Applications and Technologies. Piscataway， NJ： IEEE Press， 2018： 136-141.

［14］Hu Yanmei， Yang Bo， Lyu Chenyang. A local dynamic method for tracking communities and their evolution in dynamic networks［J］. Knowledge-Based Systems， 2016， 110： 176-190.

［15］Al-Sharoa E， Al-Khassaweneh M， Aviyente S. Tensor based temporal and multilayer community detection for studying brain dynamics during resting state fMRI ［J］. IEEE Trans on Biomedical Engineering， 2019， 66（3）： 695-709.

［16］Sariyüce A E， Gedik B， Jacques-Silva G， et al. SONIC： streaming overlapping community detection ［J］. Data Mining and Knowledge Discovery， 2016， 30（4）： 819-847.

［17］Li Xiaoming， Wu Bin， Guo Qian， et al. Dynamic community detection algorithm based on incremental identification ［C］// Proc of IEEE International Conference on Data Mining Workshop. Pisca-taway， NJ： IEEE Press， 2015： 900-907.

［18］Chi Yun， Song Xiaodan， Zhou Dengyong， et al. On evolutionary spectral clustering ［J］. ACM Trans on Knowledge Discovery from Data， 2009， 3（4）： 1-30.

［19］Lin Yuru， Chi Yun， Zhu Shenghuo， et al. Analyzing communities and their evolutions in dynamic social networks［J］. ACM Trans on Knowledge Discovery from Data， 2009， 3（2）： 1-31.

［20］Folino F， Pizzuti C. An evolutionary multiobjective approach for community discovery in dynamic networks ［J］. IEEE Trans on Know-ledge amp; Data Engineering， 2014， 26（8）： 1838-1852.

［21］Yu Wei， Wang Wenjun， Jiao Pengfei， et al. Evolutionary clustering via graph regularized nonnegative matrix factorization for exploring temporal networks ［J］. Knowledge-Based Systems， 2019， 167： 1-10.

［22］Yin Ying， Zhao Yuhai， Li He， et al. Multi-objective evolutionary clustering for large-scale dynamic community detection［J］. Information Sciences， 2021， 549： 269-287.

［23］Ma Xiaoke， Zhang Benhui， Ma Changzhou， et al. Co-regularized nonnegative matrix factorization for evolving community detection in dynamic networks［J］. Information Sciences， 2020， 528： 265-279.

［24］Wang Shuaihui， Li Guopeng， Hu Guyu， et al. Community detection in dynamic networks using constraint non-negative matrix factorization ［J］. Intelligent Data Analysis， 2020， 24（1）： 119-139.

［25］Li Dongyuan， Zhong Xiaoxiong， Dou Zengfa， et al. Detecting dyna-mic community by fusing network embedding and nonnegative matrix factorization ［J］. Knowledge-Based Systems， 2021， 221： 106961.

［26］Wang Zhen， Wang Chunyu， Li Xianghua， et al. Evolutionary Markov dynamics for network community detection ［J］. IEEE Trans on Knowledge and Data Engineering， 2022， 34（3）： 1206-1220.

［27］Kim M S， Han Jiawei. A particle-and-density based evolutionary clustering method for dynamic networks ［J］. Proceedings of the VLDB Endowment， 2009， 2（1）： 622-633.

［28］Jiao Pengfei， Yu Wei， Wang Wenjun， et al. Exploring temporal community structure and constant evolutionary pattern hiding in dynamic networks［J］. Neurocomputing， 2018， 314： 224-233.

［29］Jiao Pengfei， Lyu Haodong， Li Xiaoming， et al. Temporal community detection based on symmetric nonnegative matrix factorization ［J］. International Journal of Modern Physics B， 2017， 31（13）： 1750102.

［30］Márquez R， Weber R. Dynamic community detection including node attributes ［J］. Expert Systems with Applications， 2023， 223： 119791.

［31］Lancichinetti A， Fortunato S. Benchmarks for testing community detection algorithms on directed and weighted graphs with overlapping communities ［J］. Physical Review E Statistical Nonlinear amp; Soft Matter Physics， 2009， 80（2）： 016118.